اثبات اسنل دکارت
-
پوري فيزيكدان
عضویت : چهارشنبه ۱۳۹۰/۴/۱ - ۱۳:۱۴
پست: 27-
- klausmeister
عضویت : یکشنبه ۱۳۸۸/۳/۳۱ - ۱۰:۰۸
پست: 200-
سپاس: 69
تماس:
-
StyleOwner
عضویت : یکشنبه ۱۴۰۱/۴/۵ - ۰۳:۵۳
پست: 1-
- جنسیت:
اثبات رابطه ی اسنل
ببینید این رابطه رو اسنل کشف کرده (sin1n1=sin2n2) ولی اثبات نداره یعنی کسی اثباتش رو بلد نیست و اینکه بگم این رابطه ی کشف شده تا الان جواب داده و صدق کرده در حد کتاب دبیرستان بت بگم اگه یه معلم نوب سگ اومد بت گفت اثبات کن بگو بر اساس اینکه ضریب شکست هر محیط برابر است با n=C/V پس ضریب شکست با سرعت رابطه ی عکس داره و از طرفی سرعت با طول موج و سینوس زاویه ی موج با خط عمود رابطه ی مستقیم داره بنابر این در کل
n1/n2=v2/v1=sin2/sin1
n1sin1=n2sin2
چیکار کنیم دیگه معلما و استادامون گاون
n1/n2=v2/v1=sin2/sin1
n1sin1=n2sin2
چیکار کنیم دیگه معلما و استادامون گاون
- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: اثبات اسنل دکارت
من رشته درسی ام چیز دیگه هست فقط میدونم از اصل فرما میاد .بازم برات پیدا کردم .البته سخت نبود یادم اومد اخه و دبیرستان مبحث نور خوندم.
قانون اسنل را می توان از اصل فرما استخراج کرد که می گوید نور مسیری را طی می کند که کمترین زمان را می گیرد. با گرفتن مشتق طول مسیر نوری، نقطه ثابت مسیر طی شده توسط نور پیدا میشه.نور از محیط 1، نقطه Q، وارد محیط 2 می شود، شکست رخ می دهد و در نهایت به نقطه P می رسد.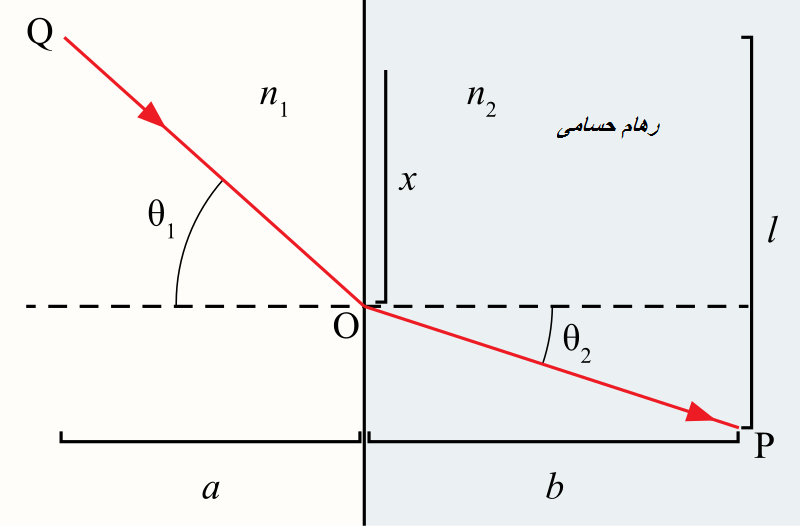
همانطور که در شکل سمت راست نشان داده شده است، ضریب شکست محیط 1 و متوسط 2 را به ترتیب ${\displaystyle n_{1}}$و ${\displaystyle n_{2}}$ فرض کنید. نور از طریق نقطه O از محیط 1 وارد محیط 2 می شود.${\displaystyle \theta _{1}}$زاویه تابش است،$ {\displaystyle \theta _{2}}$ زاویه شکست نسبت به حالت عادی است.سرعت فاز نور در محیط 1 و محیط 2 می باشد
${\displaystyle v_{1}=c/n_{1}}$ و
به ترتیب ${\displaystyle v_{2}=c/n_{2}}$
${\displaystyle c}$ سرعت نور در خلاء است.
فرض کنید T زمان لازم برای عبور نور از نقطه Q از نقطه O به نقطه P باشد.
${\displaystyle T={\frac {\sqrt {x^{2}+a^{2}}}{v_{1}}}+{\frac {\sqrt {b^{2}+(l-x)^{2}}}{v_{2}}}={\frac {\sqrt {x^{2}+a^{2}}}{v_{1}}}+{\frac {\sqrt {b^{2}+l^{2}-2lx+x^{2}}}{v_{2}}}}$
که در آن a، b، l و x در شکل سمت راست نشان داده شده است، x پارامتر متغیر است.
${\displaystyle {\frac {dT}{dx}}={\frac {x}{v_{1}{\sqrt {x^{2}+a^{2}}}}}+{\frac {-(l-x)}{v_{2}{\sqrt {(l-x)^{2}+b^{2}}}}}=0}$ (نقطه ثابت)
توجه داشته باشید که ${\displaystyle {\frac {x}{\sqrt {x^{2}+a^{2}}}}=\sin \theta _{1}}$
و ${\displaystyle {\frac {l-x}{\sqrt {(l-x)^{2}+b^{2}}}}=\sin \theta _{2}}$
از این رومن دارم بقیه اش ساده هست
${\displaystyle {\frac {dT}{dx}}={\frac {\sin \theta _{1}}{v_{1}}}-{\frac {\sin \theta _{2}}{v_ {2}}}=0}$
${\displaystyle {\frac {\sin \theta _{1}}{v_{1}}}={\frac {\sin \theta _{2}}{v_{2}}}}$
${\displaystyle {\frac {n_{1}\sin \theta _{1}}{c}}={\frac {n_{2}\sin \theta _{2}}{c}}}$
${\displaystyle n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}}$
ببین اثبات هندسی ساده برای قانون شکست اسنل قانون شکست اسنل را می توان از اصل فرما به دست آورید که نور مسیرهایی را طی میکنه که با استفاده از حساب ساده، زمان را به حداقل می رساند.دو پرتو موازی A و B را در نظر بگیرید که از محیط 1 (مثلاً هوا) به محیط 2 (مثلاً آب) می آیند. پس از رسیدن به رابط $\mathcal{L}$ بین دو رسانه (هوا و آب)، مسیر موازی خود را به ترتیب در جهات U و V ادامه می دهند.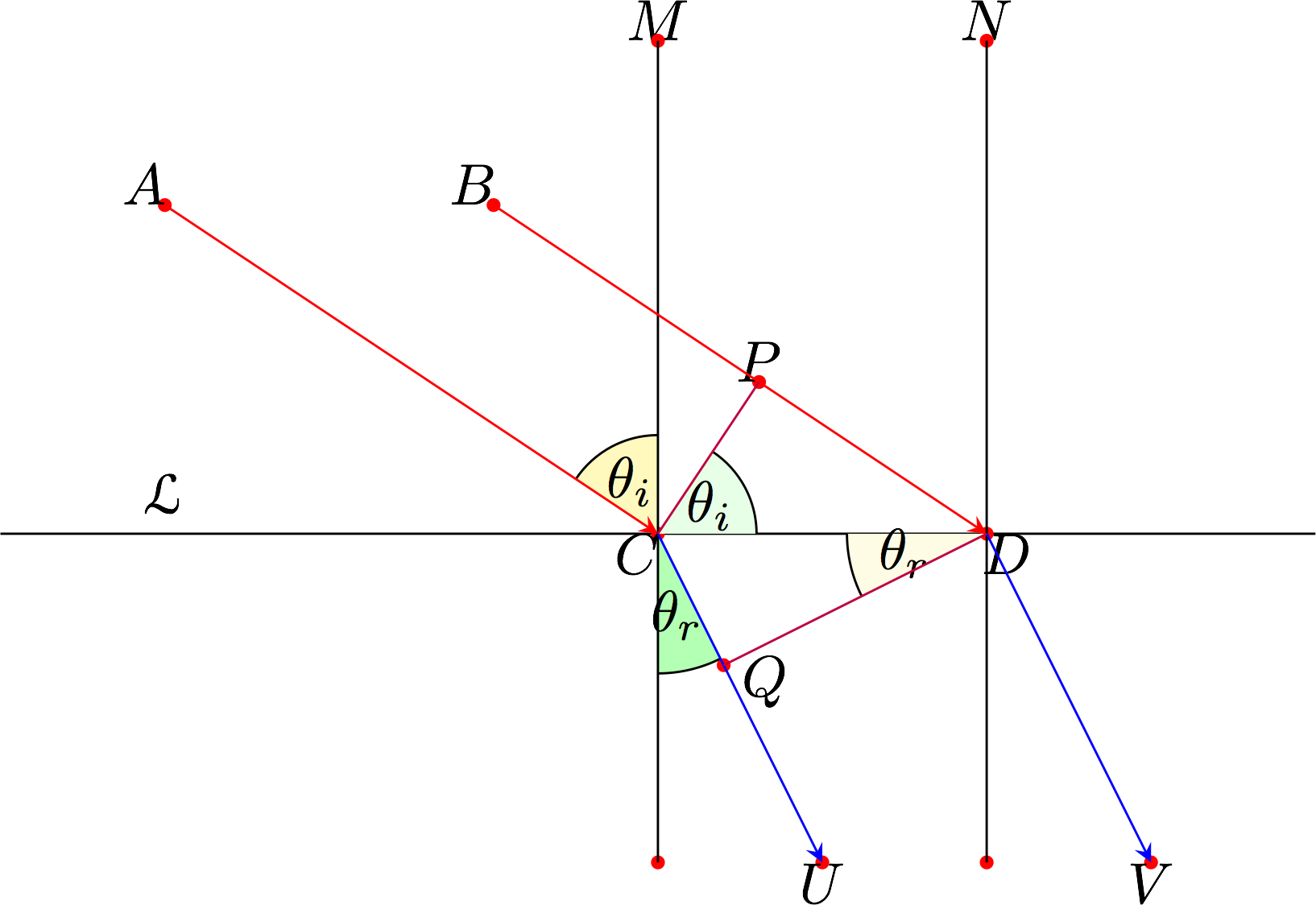
فرض کنید در زمان t=0، پرتو نور A به رابط $\mathcal{L}$ در نقطه C می رسد، در حالی که پرتو B هنوز با فاصله PD از سطح دور است. B با سرعت $v_{1}=\frac{c}{n_{1}}$ حرکت می کند و در t ثانیه به D می رسد. در طول این بازه زمانی، پرتو A به سیر خود در محیط 2 با سرعت $v_{2}=\frac{c}{n_{2}}$ ادامه می دهد و به نقطه Q می رسد.
ما می توانیم بقیه را به صورت هندسی (با نگاه کردن به خطوط موازی) از شکل فرمول بندی کنیم. اجازه دهید x نشان دهنده فاصله بین C و D باشد.
$\begin{eqnarray*}
x \sin\left(\theta_{i}\right) &=& PD \\
&=& v_{1} t \\
&=& \frac{c}{n_{1}} t \\
x \sin\left(\theta_{r}\right) &=& CQ \\
&=& v_{2} t \\
&=& \frac{c}{n_{2}} t
\end{eqnarray*}$
بدین ترتیب$\begin{eqnarray*}
n_{1} \sin\left(\theta_{i}\right) &=& \frac{c}{x} t \\
n_{2} \sin\left(\theta_{r}\right) &=& \frac{c}{x} t
\end{eqnarray*}$
تنظیم مجدد این موضوع ما را به قانون اسنل همانطور که می دانیم می برد.
$\begin{eqnarray*}
\frac{n_{2} }{n_{1}} &=& \frac{\sin\left(\theta_{i}\right) }{ \sin\left(\theta_{r}\right)}
\end{eqnarray*}$انکسار یک پرتو فرودی معمولی از دیدگاه قانون شکست
$\sin\theta_1/\sin\theta_2=v_1/v_2$
چگونه می توان این مورد را توجیه کرد که پرتو فرودی عمودی وارد می شود (طبیعی تا مرز، یعنی θ1=0)؟
دقت کن با اصل فرما من کمترین زمان رسیدن میدونم و مشتق میگیرم $t=\frac{\sqrt{a^2+x^2}}{v}+\frac{\sqrt{b^2+(d-x)^2}}{v'}$
شکل ببین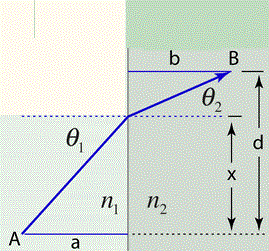 حال ببین $\frac{dt}{dx}=\frac{x}{v\sqrt{a^2+x^2}}-\frac{d-x}{v'\sqrt{b^2+(d-x)^2}}=0$خوب این معادل است با $\frac{\sin(\theta_{1})}{v}=\frac{\sin(\theta_{2})}{v'}$
حال ببین $\frac{dt}{dx}=\frac{x}{v\sqrt{a^2+x^2}}-\frac{d-x}{v'\sqrt{b^2+(d-x)^2}}=0$خوب این معادل است با $\frac{\sin(\theta_{1})}{v}=\frac{\sin(\theta_{2})}{v'}$
اگر پرتو فرودی شما وارد سطح x=0 نرمال شد، دوباره همان اصل را بنویسید (کلی نگه دارید)
$t=\frac{\sqrt{a^2+x^2}}{v}+\frac{\sqrt{b^2+(d-x)^2}}{v'}$بنابراین $\frac{dt}{dx}=0-\frac{d}{v'\sqrt{b^2+d^2}}=0$
و این ممکن است اگر$d=0 \rightarrow d-x=0$
حالا میگیم چرا اصل فرما در واقع یک اصل حداقل زمانه. آنچه می گوید این است که از بین تمام مسیرهای ممکن بین دو نقطه، نور مسیری را دنبال می کند که زمان صرف شده برای پیمودن آن مسیر را به حداقل می رساند.
میدونیم که اگر سرعت نور در سراسر محیط ثابت باشد در خطوط مستقیم حرکت می کند، اما در فصل مشترک دو رسانه که نور سرعت انتشار آن را تغییر می دهد، فرض می کنیم که نمی دانیم پرتو نور چگونه می زند (به عبارت دیگر، ما زوایای فرود و شکست ناشناخته ای داریم.ما قانون اسنل را استخراج می کنیم.
فرض کنید پرتو نور در نقطه P1 ساطع می شود و می خواهد در کمترین زمان ممکن به نقطه P2 برسد. این نقاط ثابت هستند و مختصات آنها $P_1(0,h_1), P_2(-h_2, D)$ است. اکنون میخواهیم زمان طی شده در مجموعه مسیرهای احتمالی را به حداقل برسانیم. فرض کنید که پرتو نور در فاصله تابشی d1 از P1 و d2 از P2 فاصله دارد. می دانیم که $d_1+d_2=D$ همچنین کل زمان سفر بین دو نقطه اینجا اوردم $T(d_1,d_2)=t_1+t_2=\frac{L_1}{v_1}+\frac{L_2}{v_2}=\frac{1}{c}\Big[n_1\sqrt{d_1^2+h_1^2}+n_2\sqrt{d_2^2+h_2^2}\Big]~~, ~~ d_1+d_2=D$
اکنون می خواهیم T را با استفاده از روشهای استاندارد ضربکننده لاگرانژ$\tilde{T}=T(d_1,d_2)-\lambda(d_1+d_2-D)$
و محاسبه می کنیم$\frac{\partial\tilde{T}}{\partial d_1}=\frac{n_1d_1}{c\sqrt{d_1^2+h_1^2}}-\lambda=0\\
\frac{\partial\tilde{T}}{\partial d_2}=\frac{n_2d_2}{c\sqrt{d_2^2+h_2^2}}-\lambda=0$
توجه کنید که $\sin\theta_1=\frac{d_1}{\sqrt{d_1^2+h_1^2}}$ و به طور مشابه برای زاویه تابش (فقط شاخص 1 را با 2 تعویض کنید) و بنابراین بلافاصله دریافت می کنیم که:$n_1\sin\theta_1=n_2\sin\theta_2=\lambda$
من حدس میزنم نکتهای که فرما واقعاً میگوید این است که زمان طی شده در طول یک مسیر به حداقل میرسد. بنابراین وقتی برخی از نویسندگان می گویند طول مسیر هوا، این در واقع به معنای زمان است. برای درک اینکه چرا آنها چنین می گویند، فرض کنید ضریب شکست به طور مداوم در فضا تغییر می کند. سپس باید به حداقل برسیم $T=\int_{trajectory}dt=\int{\frac{ds}{v(s)}}=\frac{1}{c}\int_{P_1\rightarrow P_2}n(x(s), y(s))ds$
و این را می توان با استفاده از روش های حساب استاندارد تغییرات به حداقل رساند. آخرین کمیت (شاید حذف سرعت نور) "طول مسیر" است که آنها در مورد آن صحبت می کنند، زیرا در انتگرال طول مسیر واقعی ds در نظر گرفته می شود، اما با یک تابع معین از فضازمان، یعنی ضریب شکست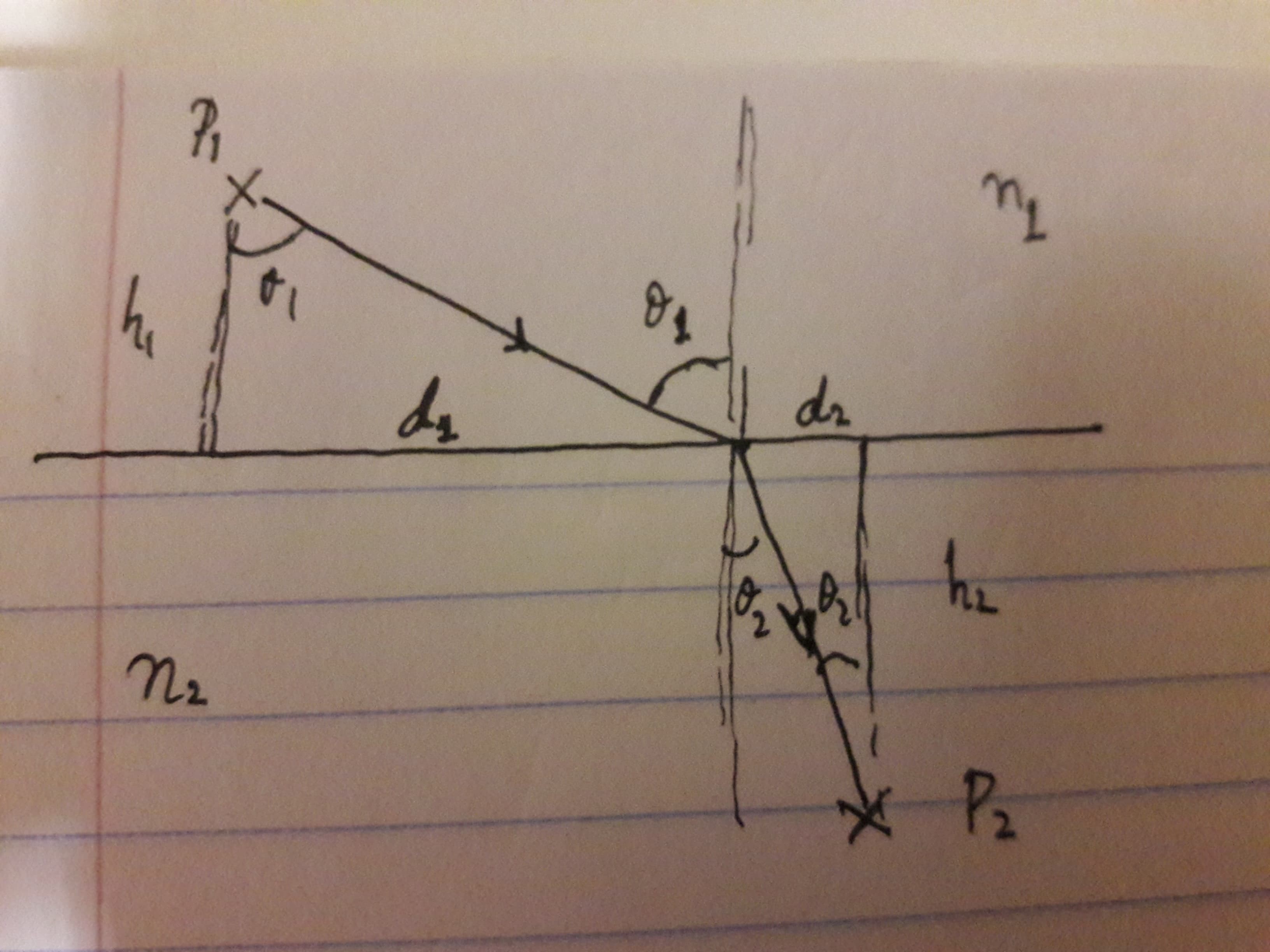
امیدوارم این مفید باشد!.hope I helped you understand the question. Roham Hesami, sixth
semester of aerospace engineering

 رهام حسامی ترم ششم مهندسی هوافضا
رهام حسامی ترم ششم مهندسی هوافضا
قانون اسنل را می توان از اصل فرما استخراج کرد که می گوید نور مسیری را طی می کند که کمترین زمان را می گیرد. با گرفتن مشتق طول مسیر نوری، نقطه ثابت مسیر طی شده توسط نور پیدا میشه.نور از محیط 1، نقطه Q، وارد محیط 2 می شود، شکست رخ می دهد و در نهایت به نقطه P می رسد.

همانطور که در شکل سمت راست نشان داده شده است، ضریب شکست محیط 1 و متوسط 2 را به ترتیب ${\displaystyle n_{1}}$و ${\displaystyle n_{2}}$ فرض کنید. نور از طریق نقطه O از محیط 1 وارد محیط 2 می شود.${\displaystyle \theta _{1}}$زاویه تابش است،$ {\displaystyle \theta _{2}}$ زاویه شکست نسبت به حالت عادی است.سرعت فاز نور در محیط 1 و محیط 2 می باشد
${\displaystyle v_{1}=c/n_{1}}$ و
به ترتیب ${\displaystyle v_{2}=c/n_{2}}$
${\displaystyle c}$ سرعت نور در خلاء است.
فرض کنید T زمان لازم برای عبور نور از نقطه Q از نقطه O به نقطه P باشد.
${\displaystyle T={\frac {\sqrt {x^{2}+a^{2}}}{v_{1}}}+{\frac {\sqrt {b^{2}+(l-x)^{2}}}{v_{2}}}={\frac {\sqrt {x^{2}+a^{2}}}{v_{1}}}+{\frac {\sqrt {b^{2}+l^{2}-2lx+x^{2}}}{v_{2}}}}$
که در آن a، b، l و x در شکل سمت راست نشان داده شده است، x پارامتر متغیر است.
${\displaystyle {\frac {dT}{dx}}={\frac {x}{v_{1}{\sqrt {x^{2}+a^{2}}}}}+{\frac {-(l-x)}{v_{2}{\sqrt {(l-x)^{2}+b^{2}}}}}=0}$ (نقطه ثابت)
توجه داشته باشید که ${\displaystyle {\frac {x}{\sqrt {x^{2}+a^{2}}}}=\sin \theta _{1}}$
و ${\displaystyle {\frac {l-x}{\sqrt {(l-x)^{2}+b^{2}}}}=\sin \theta _{2}}$
از این رومن دارم بقیه اش ساده هست
${\displaystyle {\frac {dT}{dx}}={\frac {\sin \theta _{1}}{v_{1}}}-{\frac {\sin \theta _{2}}{v_ {2}}}=0}$
${\displaystyle {\frac {\sin \theta _{1}}{v_{1}}}={\frac {\sin \theta _{2}}{v_{2}}}}$
${\displaystyle {\frac {n_{1}\sin \theta _{1}}{c}}={\frac {n_{2}\sin \theta _{2}}{c}}}$
${\displaystyle n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}}$
ببین اثبات هندسی ساده برای قانون شکست اسنل قانون شکست اسنل را می توان از اصل فرما به دست آورید که نور مسیرهایی را طی میکنه که با استفاده از حساب ساده، زمان را به حداقل می رساند.دو پرتو موازی A و B را در نظر بگیرید که از محیط 1 (مثلاً هوا) به محیط 2 (مثلاً آب) می آیند. پس از رسیدن به رابط $\mathcal{L}$ بین دو رسانه (هوا و آب)، مسیر موازی خود را به ترتیب در جهات U و V ادامه می دهند.

فرض کنید در زمان t=0، پرتو نور A به رابط $\mathcal{L}$ در نقطه C می رسد، در حالی که پرتو B هنوز با فاصله PD از سطح دور است. B با سرعت $v_{1}=\frac{c}{n_{1}}$ حرکت می کند و در t ثانیه به D می رسد. در طول این بازه زمانی، پرتو A به سیر خود در محیط 2 با سرعت $v_{2}=\frac{c}{n_{2}}$ ادامه می دهد و به نقطه Q می رسد.
ما می توانیم بقیه را به صورت هندسی (با نگاه کردن به خطوط موازی) از شکل فرمول بندی کنیم. اجازه دهید x نشان دهنده فاصله بین C و D باشد.
$\begin{eqnarray*}
x \sin\left(\theta_{i}\right) &=& PD \\
&=& v_{1} t \\
&=& \frac{c}{n_{1}} t \\
x \sin\left(\theta_{r}\right) &=& CQ \\
&=& v_{2} t \\
&=& \frac{c}{n_{2}} t
\end{eqnarray*}$
بدین ترتیب$\begin{eqnarray*}
n_{1} \sin\left(\theta_{i}\right) &=& \frac{c}{x} t \\
n_{2} \sin\left(\theta_{r}\right) &=& \frac{c}{x} t
\end{eqnarray*}$
تنظیم مجدد این موضوع ما را به قانون اسنل همانطور که می دانیم می برد.
$\begin{eqnarray*}
\frac{n_{2} }{n_{1}} &=& \frac{\sin\left(\theta_{i}\right) }{ \sin\left(\theta_{r}\right)}
\end{eqnarray*}$انکسار یک پرتو فرودی معمولی از دیدگاه قانون شکست
$\sin\theta_1/\sin\theta_2=v_1/v_2$
چگونه می توان این مورد را توجیه کرد که پرتو فرودی عمودی وارد می شود (طبیعی تا مرز، یعنی θ1=0)؟
دقت کن با اصل فرما من کمترین زمان رسیدن میدونم و مشتق میگیرم $t=\frac{\sqrt{a^2+x^2}}{v}+\frac{\sqrt{b^2+(d-x)^2}}{v'}$
شکل ببین
 حال ببین $\frac{dt}{dx}=\frac{x}{v\sqrt{a^2+x^2}}-\frac{d-x}{v'\sqrt{b^2+(d-x)^2}}=0$خوب این معادل است با $\frac{\sin(\theta_{1})}{v}=\frac{\sin(\theta_{2})}{v'}$
حال ببین $\frac{dt}{dx}=\frac{x}{v\sqrt{a^2+x^2}}-\frac{d-x}{v'\sqrt{b^2+(d-x)^2}}=0$خوب این معادل است با $\frac{\sin(\theta_{1})}{v}=\frac{\sin(\theta_{2})}{v'}$اگر پرتو فرودی شما وارد سطح x=0 نرمال شد، دوباره همان اصل را بنویسید (کلی نگه دارید)
$t=\frac{\sqrt{a^2+x^2}}{v}+\frac{\sqrt{b^2+(d-x)^2}}{v'}$بنابراین $\frac{dt}{dx}=0-\frac{d}{v'\sqrt{b^2+d^2}}=0$
و این ممکن است اگر$d=0 \rightarrow d-x=0$
حالا میگیم چرا اصل فرما در واقع یک اصل حداقل زمانه. آنچه می گوید این است که از بین تمام مسیرهای ممکن بین دو نقطه، نور مسیری را دنبال می کند که زمان صرف شده برای پیمودن آن مسیر را به حداقل می رساند.
میدونیم که اگر سرعت نور در سراسر محیط ثابت باشد در خطوط مستقیم حرکت می کند، اما در فصل مشترک دو رسانه که نور سرعت انتشار آن را تغییر می دهد، فرض می کنیم که نمی دانیم پرتو نور چگونه می زند (به عبارت دیگر، ما زوایای فرود و شکست ناشناخته ای داریم.ما قانون اسنل را استخراج می کنیم.
فرض کنید پرتو نور در نقطه P1 ساطع می شود و می خواهد در کمترین زمان ممکن به نقطه P2 برسد. این نقاط ثابت هستند و مختصات آنها $P_1(0,h_1), P_2(-h_2, D)$ است. اکنون میخواهیم زمان طی شده در مجموعه مسیرهای احتمالی را به حداقل برسانیم. فرض کنید که پرتو نور در فاصله تابشی d1 از P1 و d2 از P2 فاصله دارد. می دانیم که $d_1+d_2=D$ همچنین کل زمان سفر بین دو نقطه اینجا اوردم $T(d_1,d_2)=t_1+t_2=\frac{L_1}{v_1}+\frac{L_2}{v_2}=\frac{1}{c}\Big[n_1\sqrt{d_1^2+h_1^2}+n_2\sqrt{d_2^2+h_2^2}\Big]~~, ~~ d_1+d_2=D$
اکنون می خواهیم T را با استفاده از روشهای استاندارد ضربکننده لاگرانژ$\tilde{T}=T(d_1,d_2)-\lambda(d_1+d_2-D)$
و محاسبه می کنیم$\frac{\partial\tilde{T}}{\partial d_1}=\frac{n_1d_1}{c\sqrt{d_1^2+h_1^2}}-\lambda=0\\
\frac{\partial\tilde{T}}{\partial d_2}=\frac{n_2d_2}{c\sqrt{d_2^2+h_2^2}}-\lambda=0$
توجه کنید که $\sin\theta_1=\frac{d_1}{\sqrt{d_1^2+h_1^2}}$ و به طور مشابه برای زاویه تابش (فقط شاخص 1 را با 2 تعویض کنید) و بنابراین بلافاصله دریافت می کنیم که:$n_1\sin\theta_1=n_2\sin\theta_2=\lambda$
من حدس میزنم نکتهای که فرما واقعاً میگوید این است که زمان طی شده در طول یک مسیر به حداقل میرسد. بنابراین وقتی برخی از نویسندگان می گویند طول مسیر هوا، این در واقع به معنای زمان است. برای درک اینکه چرا آنها چنین می گویند، فرض کنید ضریب شکست به طور مداوم در فضا تغییر می کند. سپس باید به حداقل برسیم $T=\int_{trajectory}dt=\int{\frac{ds}{v(s)}}=\frac{1}{c}\int_{P_1\rightarrow P_2}n(x(s), y(s))ds$
و این را می توان با استفاده از روش های حساب استاندارد تغییرات به حداقل رساند. آخرین کمیت (شاید حذف سرعت نور) "طول مسیر" است که آنها در مورد آن صحبت می کنند، زیرا در انتگرال طول مسیر واقعی ds در نظر گرفته می شود، اما با یک تابع معین از فضازمان، یعنی ضریب شکست

امیدوارم این مفید باشد!.hope I helped you understand the question. Roham Hesami, sixth
semester of aerospace engineering



