مشتق شتاب
-
winterwoman
نام: سارا عبدلي
عضویت : شنبه ۱۳۹۰/۱۱/۲۲ - ۲۲:۰۵
پست: 6-
Re: يه سوال فوووووووري !
خب آره.هم مشتقش و هم مشتقِ مشتقش و هم ...
به مشتق شتاب هم گاهی اوقات " جرک " میگن.ولی چیزی که مسلمه به هر حال یه مفهومی فیزیکی هست.
به مشتق شتاب هم گاهی اوقات " جرک " میگن.ولی چیزی که مسلمه به هر حال یه مفهومی فیزیکی هست.
دوای درد عاشق را کسی کو سهل پندارد
ز فکر آنان که در تدبیر درمانند در مانند
ز فکر آنان که در تدبیر درمانند در مانند
-
winterwoman
نام: سارا عبدلي
عضویت : شنبه ۱۳۹۰/۱۱/۲۲ - ۲۲:۰۵
پست: 6-
Re: يه سوال فوووووووري !
Cartouche نوشته شده:خب آره.هم مشتقش و هم مشتقِ مشتقش و هم ...
به مشتق شتاب هم گاهی اوقات " جرک " میگن.ولی چیزی که مسلمه به هر حال یه مفهومی فیزیکی هست.
ميشه لطفا كمي برام توضيح بدين؟
اين سوال رو استاد فيزيك پرسيد ازمون..
اگه لينكي هم هست كه ممنون ميشم
Re: سوال : مشتق شتاب
نه لینکی نمیشناسم ، تو کتابِ فیزیکی هم تا به حال ندیدم که از عنوان "جرک" استفاده کنن.
همونطور که سرعت مشتق مکانه ، و شتاب هم مشتق سرعته (البته زمانی) ، جرک هم مشتق زمانی شتاب هستش.و طبیعتا همونطور که مکان ، سرعت و شتاب مفاهیمی فیزیکی هستن ، خب جرک و مشتقات آن هم مفاهیمی فیزیک میشن دیگه.
خیلی هم کاربرد نداره ، ولی مثلا چطور وقتی شتاب ثابته ، ما میگیم x=v0t+1/2at^2
وقتی هم که جرک ثابت باشه و شتاب متغیر میگیم : x=v0t+1/2a0t^2+1/6jt^3
( حرف j رو همینطوری خودم براش گذشتم ، چون فکر نکنم که نمادی داشته باشه)
و دوباره میگم ، عنوان « جِرک» بیشتر یه اصطلاح مهندسی هستشو و در ارتعاشات و مهندسی مکانیک و سیالات هم کاربرد زیادی داره ولی تو فیزیک کاربرد چندانی نداره .ولی خب به هر حال یه مفهوم فیزیکی هست.
همونطور که سرعت مشتق مکانه ، و شتاب هم مشتق سرعته (البته زمانی) ، جرک هم مشتق زمانی شتاب هستش.و طبیعتا همونطور که مکان ، سرعت و شتاب مفاهیمی فیزیکی هستن ، خب جرک و مشتقات آن هم مفاهیمی فیزیک میشن دیگه.
خیلی هم کاربرد نداره ، ولی مثلا چطور وقتی شتاب ثابته ، ما میگیم x=v0t+1/2at^2
وقتی هم که جرک ثابت باشه و شتاب متغیر میگیم : x=v0t+1/2a0t^2+1/6jt^3
( حرف j رو همینطوری خودم براش گذشتم ، چون فکر نکنم که نمادی داشته باشه)
و دوباره میگم ، عنوان « جِرک» بیشتر یه اصطلاح مهندسی هستشو و در ارتعاشات و مهندسی مکانیک و سیالات هم کاربرد زیادی داره ولی تو فیزیک کاربرد چندانی نداره .ولی خب به هر حال یه مفهوم فیزیکی هست.
دوای درد عاشق را کسی کو سهل پندارد
ز فکر آنان که در تدبیر درمانند در مانند
ز فکر آنان که در تدبیر درمانند در مانند
-
winterwoman
نام: سارا عبدلي
عضویت : شنبه ۱۳۹۰/۱۱/۲۲ - ۲۲:۰۵
پست: 6-
Re: سوال : مشتق شتاب
Cartouche نوشته شده:نه لینکی نمیشناسم ، تو کتابِ فیزیکی هم تا به حال ندیدم که از عنوان "جرک" استفاده کنن.
همونطور که سرعت مشتق مکانه ، و شتاب هم مشتق سرعته (البته زمانی) ، جرک هم مشتق زمانی شتاب هستش.و طبیعتا همونطور که مکان ، سرعت و شتاب مفاهیمی فیزیکی هستن ، خب جرک و مشتقات آن هم مفاهیمی فیزیک میشن دیگه.
خیلی هم کاربرد نداره ، ولی مثلا چطور وقتی شتاب ثابته ، ما میگیم x=v0t+1/2at^2
وقتی هم که جرک ثابت باشه و شتاب متغیر میگیم : x=v0t+1/2a0t^2+1/6jt^3
( حرف j رو همینطوری خودم براش گذشتم ، چون فکر نکنم که نمادی داشته باشه)
و دوباره میگم ، عنوان « جِرک» بیشتر یه اصطلاح مهندسی هستشو و در ارتعاشات و مهندسی مکانیک و سیالات هم کاربرد زیادی داره ولی تو فیزیک کاربرد چندانی نداره .ولی خب به هر حال یه مفهوم فیزیکی هست.
مرسي
جالبه
من شتاب رو ميفهمم! اما جرك رو درك نميكنم.. معني هندسي جرك چيه؟
فردا كلاس فيزيك دارم.خوشحال و ممنون ميشم اگه برام يه ذره توضيح بدين
لطفا!
Re: سوال : مشتق شتاب
شتاب رو که میدونین چیه.شتاب آهنگ تغییر سرعته.وقتی که سرعت ثابت نباشه ، میتونیم براش یه آهنگ تغییر تعریف کنیم.
حالا اگه شتاب هم ثابت نباشه ، ما میتونیم براش یه آهنگ تغییر ِ نا صفر تعریف کنیم دیگه .معنیه هندسی هم نمیدونم منظورتون چیه .ولی خب جرک شیب نمودار شتاب زمان هستش.همونطور که شتاب شیب نمدار سرعت زمان هست.
به طور مثال فرض کنین ، مکان یه جسم به صورت x=5t^3 تابع زمان باشه.
حالا تو این حرکت ، سرعت 15t^2 هست ، که تابعی از زمانه.شتاب هم 30t هستش ، که بازم تابعی از زمانه.جرک هم که میشه مشتق شتاب ، برابر ثابتِ 30 هست ، که تابع زمان نیست.
حالا ممکنه تابع به صورت دیگه ای باشه که جرک هم تابع زمان باشه.
هیچ چیز خاصی نیست ، برای درک کردن ، و صرفا یه نامگذاریه.همونطور که به مشتق سزعت میگیم شتاب ، به مشتق شتاب هم میگیم جرک.
ویرایش :
من دنبال لینکی برات گشتم ، ولی بهتر از ویکی پدیا پیدا نکردم.
http://en.wikipedia.org/wiki/Jerk_%28physics%29
حالا اگه شتاب هم ثابت نباشه ، ما میتونیم براش یه آهنگ تغییر ِ نا صفر تعریف کنیم دیگه .معنیه هندسی هم نمیدونم منظورتون چیه .ولی خب جرک شیب نمودار شتاب زمان هستش.همونطور که شتاب شیب نمدار سرعت زمان هست.
به طور مثال فرض کنین ، مکان یه جسم به صورت x=5t^3 تابع زمان باشه.
حالا تو این حرکت ، سرعت 15t^2 هست ، که تابعی از زمانه.شتاب هم 30t هستش ، که بازم تابعی از زمانه.جرک هم که میشه مشتق شتاب ، برابر ثابتِ 30 هست ، که تابع زمان نیست.
حالا ممکنه تابع به صورت دیگه ای باشه که جرک هم تابع زمان باشه.
هیچ چیز خاصی نیست ، برای درک کردن ، و صرفا یه نامگذاریه.همونطور که به مشتق سزعت میگیم شتاب ، به مشتق شتاب هم میگیم جرک.
ویرایش :
من دنبال لینکی برات گشتم ، ولی بهتر از ویکی پدیا پیدا نکردم.
http://en.wikipedia.org/wiki/Jerk_%28physics%29
دوای درد عاشق را کسی کو سهل پندارد
ز فکر آنان که در تدبیر درمانند در مانند
ز فکر آنان که در تدبیر درمانند در مانند
-
winterwoman
نام: سارا عبدلي
عضویت : شنبه ۱۳۹۰/۱۱/۲۲ - ۲۲:۰۵
پست: 6-
Re: سوال : مشتق شتاب
Cartouche نوشته شده:شتاب رو که میدونین چیه.شتاب آهنگ تغییر سرعته.وقتی که سرعت ثابت نباشه ، میتونیم براش یه آهنگ تغییر تعریف کنیم.
حالا اگه شتاب هم ثابت نباشه ، ما میتونیم براش یه آهنگ تغییر ِ نا صفر تعریف کنیم دیگه .معنیه هندسی هم نمیدونم منظورتون چیه .ولی خب جرک شیب نمودار شتاب زمان هستش.همونطور که شتاب شیب نمدار سرعت زمان هست.
به طور مثال فرض کنین ، مکان یه جسم به صورت x=5t^3 تابع زمان باشه.
حالا تو این حرکت ، سرعت 15t^2 هست ، که تابعی از زمانه.شتاب هم 30t هستش ، که بازم تابعی از زمانه.جرک هم که میشه مشتق شتاب ، برابر ثابتِ 30 هست ، که تابع زمان نیست.
حالا ممکنه تابع به صورت دیگه ای باشه که جرک هم تابع زمان باشه.
هیچ چیز خاصی نیست ، برای درک کردن ، و صرفا یه نامگذاریه.همونطور که به مشتق سزعت میگیم شتاب ، به مشتق شتاب هم میگیم جرک.
ببخشيد انقدر سوال ميكنم..
شما آيا مفاهيمه سرعت و شتاب رو در روزمره خودتون لمس يا درك نكردين تا به حال!؟
-
winterwoman
نام: سارا عبدلي
عضویت : شنبه ۱۳۹۰/۱۱/۲۲ - ۲۲:۰۵
پست: 6-
Re: سوال : مشتق شتاب
البته مشتق شتاب به زمان "شدت" ميشه و واحدش "جرك" يا "تنش" ميشه درسته؟winterwoman نوشته شده:Cartouche نوشته شده:شتاب رو که میدونین چیه.شتاب آهنگ تغییر سرعته.وقتی که سرعت ثابت نباشه ، میتونیم براش یه آهنگ تغییر تعریف کنیم.
حالا اگه شتاب هم ثابت نباشه ، ما میتونیم براش یه آهنگ تغییر ِ نا صفر تعریف کنیم دیگه .معنیه هندسی هم نمیدونم منظورتون چیه .ولی خب جرک شیب نمودار شتاب زمان هستش.همونطور که شتاب شیب نمدار سرعت زمان هست.
به طور مثال فرض کنین ، مکان یه جسم به صورت x=5t^3 تابع زمان باشه.
حالا تو این حرکت ، سرعت 15t^2 هست ، که تابعی از زمانه.شتاب هم 30t هستش ، که بازم تابعی از زمانه.جرک هم که میشه مشتق شتاب ، برابر ثابتِ 30 هست ، که تابع زمان نیست.
حالا ممکنه تابع به صورت دیگه ای باشه که جرک هم تابع زمان باشه.
هیچ چیز خاصی نیست ، برای درک کردن ، و صرفا یه نامگذاریه.همونطور که به مشتق سزعت میگیم شتاب ، به مشتق شتاب هم میگیم جرک.
ببخشيد انقدر سوال ميكنم..
شما آيا مفاهيمه سرعت و شتاب رو در روزمره خودتون لمس يا درك نكردين تا به حال!؟
Re: سوال : مشتق شتاب
بله حق با شماست ، شتاب و سرعت زیاد در زندگی روزمره دیده میشه ، ولی جرک نه و منم زیاد نمیتونم پدیده طبیعیو پیدا کنم که توش استفاده بشه.winterwoman نوشته شده:
ببخشيد انقدر سوال ميكنم..
شما آيا مفاهيمه سرعت و شتاب رو در روزمره خودتون لمس يا درك نكردين تا به حال!؟
تنش ؟ شدت ؟تا به حال نشنیدم .عنوان تنش رو زیاد شنیدم ، ولی نه برای مشتق شتاب.ولی شدت رو برای شتاب نشنیدم.winterwoman نوشته شده: البته مشتق شتاب به زمان "شدت" ميشه و واحدش "جرك" يا "تنش" ميشه درسته؟
دوای درد عاشق را کسی کو سهل پندارد
ز فکر آنان که در تدبیر درمانند در مانند
ز فکر آنان که در تدبیر درمانند در مانند
-
winterwoman
نام: سارا عبدلي
عضویت : شنبه ۱۳۹۰/۱۱/۲۲ - ۲۲:۰۵
پست: 6-
Re: سوال : مشتق شتاب
باشه خيلي خيلي ممنونCartouche نوشته شده:بله حق با شماست ، شتاب و سرعت زیاد در زندگی روزمره دیده میشه ، ولی جرک نه و منم زیاد نمیتونم پدیده طبیعیو پیدا کنم که توش استفاده بشه.winterwoman نوشته شده:
ببخشيد انقدر سوال ميكنم..
شما آيا مفاهيمه سرعت و شتاب رو در روزمره خودتون لمس يا درك نكردين تا به حال!؟تنش ؟ شدت ؟تا به حال نشنیدم .عنوان تنش رو زیاد شنیدم ، ولی نه برای مشتق شتاب.ولی شدت رو برای شتاب نشنیدم.winterwoman نوشته شده: البته مشتق شتاب به زمان "شدت" ميشه و واحدش "جرك" يا "تنش" ميشه درسته؟
فردا استاد رو حسابي سوال پيچ ميكنم!!
Re: سوال : مشتق شتاب
تنش با کرنش باهم مطرح میشن . تنش به عامل خارجی گفته میشه که روی یه جسم ما تغییراتی به وجود بیاره . به اون تغییرات کرنش میگن و به منفی نسبت تنش به کرنش مدول گفته میشه . تنش واحدی مثل فشار داره و کرنش بدون بعد یعنی تغییرات نسبی . البته بحث تنش و کرنش مفصله و بهتر کتاب امواج و ارتعشات رو بخونی . مشتق زمانی شتاب رو من توی مکانیک تحلیلی 1 دیدم . یه نگاه دوباره می کنم به تون میگم .
اسم مشتق زمانی شتاب تکان نام داره و جرک رو من جایی نشنیدم.
اسم مشتق زمانی شتاب تکان نام داره و جرک رو من جایی نشنیدم.
آخرین ویرایش توسط Cartouche سهشنبه ۱۳۹۰/۱۲/۹ - ۲۳:۱۱, ویرایش شده کلا 1 بار
دلیل: ادغام دو پست
دلیل: ادغام دو پست
Re: سوال : مشتق شتاب
سلام اگه هنوز هم نمی دونی مفهومش چی میشه؟ تا برات یه مثال ساده بزنم.winterwoman نوشته شده: ↑شنبه ۱۳۹۰/۱۱/۲۲ - ۲۲:۱۰سلام دوستان
آيا مشتق شتاب هم مفهوم فيزيكي اي را به ما نشان ميدهد؟؟
- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3282-
سپاس: 5494
- جنسیت:
تماس:
Re: سوال : مشتق شتاب
در فیزیک، تکان یا تکان سرعتی است که در آن شتاب یک جسم نسبت به زمان تغییر می کند البته بیشتر تو مهندسی کاربرد داره ما با جرک سرکار داریم . این یک کمیت برداری است (هم قدر و هم جهت دارد). جرک معمولاً با نماد j نشان داده می شود و با m/s^3$ $(واحد SI) یا گرانش استاندارد در ثانیه (g0/s) بیان می شود.اصطلاحاتJerk) اصطلاحی است در مکانیک که به اختلاف شتاب بر زمان (نسبت تغییرات شتاب بر زمان) گفته میشود و واحد آن متر بر مکعب ثانیه استشتاب، کمیتی بُرداری است، خیز نیز کمیتی بُرداری است، و از آنجا که میتوان برای آن نوشت: a×۱/∆t∆ و ۰≤t∆، پس خیز همواره با تغییرات شتاب (a∆) همعلامت خواهد بود؛ و چون t∆ همواره مثبت است، پس خیز همواره با تغییرات شتاب (a∆) همعلامت و همجهته و چون در کمیتهای بُرداری، علامت کمیت نشاندهندهٔ جهت آن است، پس خیز همواره با تغییرات شتاب همجهته
به عنوان یک بردار، jerk j را می توان به عنوان اولین مشتق شتاب، مشتق زمان دوم سرعت، و مشتق سوم زمان از موقعیت بیان کرد:
${\displaystyle \mathbf {j} (t)={\frac {\mathrm {d} \mathbf {a} (t)}{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}\mathbf {v} (t)}{\mathrm {d} t^{2}}}={\frac {\mathrm {d} ^{3}\mathbf {r} (t)}{\mathrm {d} t^{3}}}}$
جایی که
a شتاب است
v سرعت است
r موقعیت است
زمان است
معدلات دیفرانسیل مرتبه سوم فرم
${\displaystyle J\left({\overset {\mathbf {...} }{x}},{\ddot {x}},{\dot {x}},x\right)=0}$گاهی اوقات معادلات تند و سریع نامیده می شوند. هنگامی که به یک سیستم معادل از سه معادله دیفرانسیل غیر خطی مرتبه اول معمولی تبدیل می شود، معادلات تند و سریع حداقل تنظیم برای راه حل هایی هستند که رفتار آشفته را نشان می دهند. این شرایط باعث ایجاد علاقه ریاضی در سیستم های تند و سریع می شود. سیستمهایی که مشتقهای مرتبه چهارم یا بالاتر را شامل میشوند، سیستمهای hyperjerk نامیده میشوند
احساس فشار دادن به صندلی ها در یک ماشین اسپرت پرقدرت به دلیل شتاب است. همانطور که ماشین از حالت سکون پرتاب می شود، یک حرکت مثبت بزرگ وجود دارد زیرا شتاب آن به سرعت افزایش می یابد. پس از پرتاب، یک تکان منفی کوچک و پایدار وجود دارد زیرا نیروی مقاومت هوا با افزایش سرعت خودرو افزایش مییابد، به تدریج شتاب کاهش مییابد و نیرویی که مسافر را به صندلی فشار میدهد کاهش مییابد. هنگامی که خودرو به حداکثر سرعت خود می رسد، شتاب به 0 رسیده و ثابت می ماند و پس از آن تا زمانی که راننده سرعت خود را کاهش دهد یا تغییر جهت دهد، هیچ حرکتی وجود ندارد.
هنگام ترمز ناگهانی یا در هنگام برخورد، مسافران با شتاب اولیه بیشتر از بقیه مراحل ترمز به جلو حرکت می کنند، زیرا تنش عضلانی پس از شروع ترمز یا ضربه سریعاً کنترل بدن را به دست می آورد. این اثرات در تست خودرو مدلسازی نمیشوند زیرا جسدها و آدمکهای تست تصادف کنترل فعال ماهیچهای ندارند.
برای به حداقل رساندن اثرات تند و تند، پیچهای کنار جادهها مانند پیچهای راهآهن و حلقههای ترن هوایی بهصورت کلوتوئیدی طراحی شدهاند.
نیرو، شتاب و حرکت تند
برای جرم ثابت m، شتاب a با نیروی F مطابق قانون دوم حرکت نیوتن نسبت مستقیم دارد:در چرخش
نمودار زمانبندی بیش از یک دور برای زاویه، سرعت زاویهای، شتاب زاویهای و تکانهای زاویهای
یک جسم صلب را در نظر بگیرید که حول یک محور ثابت در یک قاب مرجع اینرسی می چرخد. اگر موقعیت زاویه ای آن به عنوان تابعی از زمان θ(t) باشد، سرعت زاویه ای، شتاب و تکان را می توان به صورت زیر بیان کرد:
سرعت زاویه ای، ${\displaystyle \omega (t)={\dot {\theta }}(t)={\frac {\mathrm {d} \theta (t)}{\mathrm {d} t}}}$
حرکت تند زاویه ای، ${\displaystyle \alpha (t)={\dot {\omega }}(t)={\frac {\mathrm {d} \omega (t)}{\mathrm {d} t}}}$
,${\displaystyle \zeta (t)={\dot {\alpha }}(t)={\ddot {\omega }}(t)={\overset {...}{\theta }}(t)}$
شتاب زاویه ای برابر است با گشتاور اعمال شده روی بدنه تقسیم بر ممان اینرسی بدنه نسبت به محور لحظه ای چرخش. تغییر در گشتاور منجر به حرکت زاویه ای می شود.
حالت کلی یک جسم صلب در حال چرخش را می توان با استفاده از نظریه پیچ سینماتیکی، که شامل یک بردار محوری، سرعت زاویه ای Ω(t) و یک بردار قطبی، سرعت خطی v(t) مدل سازی کرد. از این رو، شتاب زاویه ای به صورت تعریف می شود
${\displaystyle {\boldsymbol {\alpha }}(t)={\frac {\mathrm {d} }{\mathrm {d} t}}{\boldsymbol {\Omega }}(t)={\dot {\boldsymbol {\Omega }}}(t)}$و حرکت تند و سریع زاویه ای توسط داده می شود
${\displaystyle {\boldsymbol {\zeta }}(t)={\frac {\mathrm {d} }{\mathrm {d} t}}{\boldsymbol {\alpha }}(t)={\dot {\boldsymbol {\alpha }}}(t)={\ddot {\boldsymbol {\Omega }}}(t)}$
به عنوان مثال، درایو ژنو را در نظر بگیرید، دستگاهی که برای ایجاد چرخش متناوب یک چرخ چرخ و با چرخش مداوم چرخ محرک استفاده می شود. در طول یک چرخه چرخ محرک، موقعیت زاویه ای چرخ رانده θ 90 درجه تغییر می کند و سپس ثابت می ماند. به دلیل ضخامت محدود چنگال چرخ محرک (شیار پین محرک)، این دستگاه یک ناپیوستگی در شتاب زاویه ای α و یک حرکت تند زاویه ای نامحدود ζ در چرخ رانده ایجاد می کند.
یک مارپیچ اویلر، از لحاظ نظری منحنی گذار بهینه، شتاب مرکز را به صورت خطی افزایش میدهد و منجر به تکانهای ثابت میشود (نمودار را ببینید). در کاربردهای دنیای واقعی، صفحه مسیر در امتداد بخشهای منحنی متمایل است. شیب باعث شتاب عمودی می شود که یکی از ملاحظات طراحی برای سایش در مسیر و خاکریز است. Wiener Kurve (منحنی وینی) یک منحنی ثبت شده است که برای به حداقل رساندن این سایش طراحی شده است
ترن هوایی همچنین با انتقال مسیر برای محدود کردن حرکت تند و سریع طراحی شده است. هنگام ورود به یک حلقه، مقادیر شتاب می تواند به حدود 4 g (40 متر بر ثانیه) برسد و سواری در این محیط با شتاب بالا فقط با انتقال مسیر امکان پذیر است. منحنی های S شکل، مانند شکل هشت، همچنین از انتقال مسیر برای سواری نرم استفاده می کنند.
مشتقات بالاتر (تحرک، پرش) موقعیت با توجه به زمان چگونه در فیزیک استفاده می شود
تعمیم یک مفهوم یکی از چیزهایی است که مردم معمولاً به آن نگاه می کنند تا دید بزرگ تری از یک ایده داشته باشند. بنابراین یکی از چیزهای طبیعی که باید در مورد آن تعجب کنید وقتی اینجا هستید که اگر سرعت مشتق زمانی موقعیت و شتاب مشتق زمانی سرعت است،
ترن هوایی یک مثالش
از آنجایی که معادلات حرکت مرتبه دوم هستند، مشتقات بالاتر هیچ اطلاعات جدیدی نمی دهند (اما به طور منحصر به فرد از شرایط اولیه موقعیت و سرعت پیروی می کنند)، بنابراین معمولاً مورد بحث قرار نمی گیرند.
مشتقات بالاتر در برخی از کاربردهای مهندسی، از آنجایی که حرکت حرکتی سرعت تغییر شتاب را تعیین می کند، زمانی که برخی از وسایل مکانیکی باید با نیروی ظاهری ناشی از شتاب وارد تعادل شوند، مهم است. به طور شهودی، اگر حرکت تند و سریع به نحوی بالاتر از فرکانس رزونانس باشد، ممکن است اتفاقات ناخوشایندی رخ دهد (زیرا به جای یافتن یک تعادل جدید، سیستم در عوض نوسان می کند و ممکن است شکسته شود).
این موضوع برای سیستمهای کنترلشده (مانند انسانها) که ممکن است در یک حرکت بزرگ شکسته شود، اهمیت بیشتری پیدا میکند (زیرا اگر نقطه تنظیم به سرعت تغییر کند، زمان کافی برای رسیدن به یک حالت تعادل جدید ندارد). ویکی پدیا را در این مورد ببینید.
حرکت تند و سریع در یک مورد در فیزیک در یک معادله حرکت رخ می دهد: کاهش تابشی حرکت. نیروی لورنتس-ابراهام را ببینید. به نظر میرسد که این باعث ایجاد مشکلاتی در رابطه علیت و بقای انرژی میشود (زیرا معادله راهحلی با انرژی بینهایت افزایش میدهد، اگر حرکت حرکتی اولیه ویژگیهای خاصی داشته باشد). در یک سیستم فیزیکی از این مشکلات اجتناب می شود زیرا حرکت تند و سریع اولیه در واقع آزاد نیست، بلکه توسط حرکت قبلی سیستم محدود شده است. (این مشکل به دلیل چگالی انرژی بی نهایت بار نقطه ای به وجود می آید، بنابراین به طور مستقیم از ناهماهنگی الکترودینامیک کلاسیک - به دلیل نسبیت خاص، که از الکترودینامیک کلاسیک ناشی می شود، ذرات باید نقطه مانند باشند، اما الکترودینامیک کلاسیک واگرایی هایی را نشان می دهد. هزینه های امتیازی).
در دنیای F=mv، تکانه و نیرو معادل هستند. یک جسم را به سختی فشار دهید، و بلافاصله شروع به حرکت می کند. اگر گرانش به عنوان یک نیرو عمل کند (اگر سناریوی کمی متفاوت بخواهیم باز هم می تواند یک شتاب باشد) آنگاه هر چیزی که نزدیک به یک جرم است به سمت آن حرکت می کند و به سمت چگالی های بالاتر منفجر می شود تا زمانی که فشار گرانش را متعادل کند. هیچ مداری وجود نخواهد داشت زیرا سرعت ها مستقیماً روی جرم اصلی قرار می گیرند. یک توپ رها شده از معادله x′(t)=−g پیروی می کند، یعنی x(t)=−gt+x(0): اجسام با سرعت ثابت سقوط می کنند - در واقع، وقتی توپی را پرتاب می کنید، به محض اینکه از دست شما خارج می شود و سرعت را به سرعت جاذبه تغییر می دهد.
در دنیای F=mj، شتاب ها بسیار ملایم تر خواهند بود. شما باید چیزی را بیشتر فشار دهید تا حرکت کند. یک توپ پرتاب شده از معادله x′′′(t)=−g پیروی می کند، یعنی $x(t)=-(1/6)g t^3 + a_0 t^2 + v_0t + x(0)$: اگر از حالت سکون خارج شود، طول می کشد. زمان بیشتری برای کاهش آن وجود دارد اما سرعت حتی سریعتر رشد می کند. احتمالاً ردی از شتابی که به آن دادید نیز باقی میماند: آن را محکم به سمت بالا پرتاب کنید، و نه تنها بالا میآید، بلکه برای مدتی به شتاب ادامه میدهد تا زمانی که گرانش از بین برود.
به طور کلی، می توان این بازی را بازی کرد (که سرگرم کننده است)، اما مشکل اصلی اگر از نظر ریاضی منطقی باشد. ساختار مکانیک کلاسیک نوعی نردبان است که در آن جفتهای نیرو-شتاب، تکانه-سرعت و انرژی-موقعیت به روشی درست به هم متصل میشوند و چیزهای مهمی مانند قوانین بقای تولید میکنند. این سناریوهای دیگر اساساً باید تمام فیزیک را یک پله بالا یا پایین ببرند. به این ترتیب احتمالاً میتوان لاگرانژیان و همیلتونها را به روشی معادل برای سناریوها تعریف کرد، دینامیک بسیار متفاوت و کمیتهای حفظشده را دریافت کرد، اما اساساً ساختار را ثابت نگه داشت.شتاب با نیرو تغییر می کند، بنابراین مشتق شتاب با مشتق نیرو تغییر می کند. به عبارت دیگر، اگر،
$m\ddot x = F,$
سپس،
$m\dddot x = \dot F.$
بنابراین، تند و سریع، سرعتی است که در آن نیرو در حال تغییر است، تقسیم بر جرم جسم. اگر جسمی را تکان دهید، به طور خلاصه نیروی وارد شده را از صفر به عددی تغییر می دهید، و هر چه مدت زمانی که آن را از بی نیرو به نیروی کامل برسانید، کوتاه تر است، «تحرک» عمل بیشتر می شود.نحوه محاسبه حرکت حرکتی که یک جسم را به سرعت معینی می رساند
مشکل من خیلی ساده به نظر می رسد، اما نمی توانم پاسخی پیدا کنم:
من یک جسم با سرعت مشخص v0 و شتاب a0 دارم. هدف من در زمان T سرعت جدید vx و شتاب صفر است.
چگونه می توانم تابعی را در طول زمان محاسبه کنم، که برای رسیدن به این هدف، تکان ثابت مثبت یا منفی فعلی (مشتق شتاب) را به من می دهد؟
برای مثال در دنیای واقعی، سرعت دست خود را روی دریچه گاز در نظر بگیرید. اگر موتور موشک شما نیروی رانشی متناسب با موقعیت دریچه گاز ایجاد کند، سرعت دست شما متناسب با حرکتی است که مسافران شما تجربه خواهند کرد.
یکی دیگر از کمک های شهودی ممکن است فکر کردن در مورد شتاب بر حسب گرانشی باشد که معادل آن است. اگر مسافر موشک یا آسانسور هستید و احساس میکنید وزنتان به طور ناگهانی دو برابر میشود، تند تند است. اگر وزن شما به آهستگی در حال افزایش یا کاهش است، کاهش وزن است. این به این دلیل است که وزنی که احساس می کنید متناسب با شتاب شما بالا و پایین می شود.تند و سریع (آن را j می نامیم) سومین مشتق موقعیت است. معادله معمول شما$x(t)=x_0+v_0t+\frac 12a_0t^2$ یک عبارت$\frac 1{3!}j_0t^3$اضافه می کند. می توانید از مشتقات برای دادن v(t) و a(t) استفاده کنید و سپس از نقاط شناخته شده خود برای ارزیابی پارامترها استفاده کنید. شما یک محدودیت بیش از حد دارید. شما می توانید حرکت تند را از اختلاف شتاب ها تقسیم بر زمان محاسبه کنید، اما هیچ تضمینی وجود ندارد که بتوانید تغییر سرعت مورد نظر خود را برآورده کنید.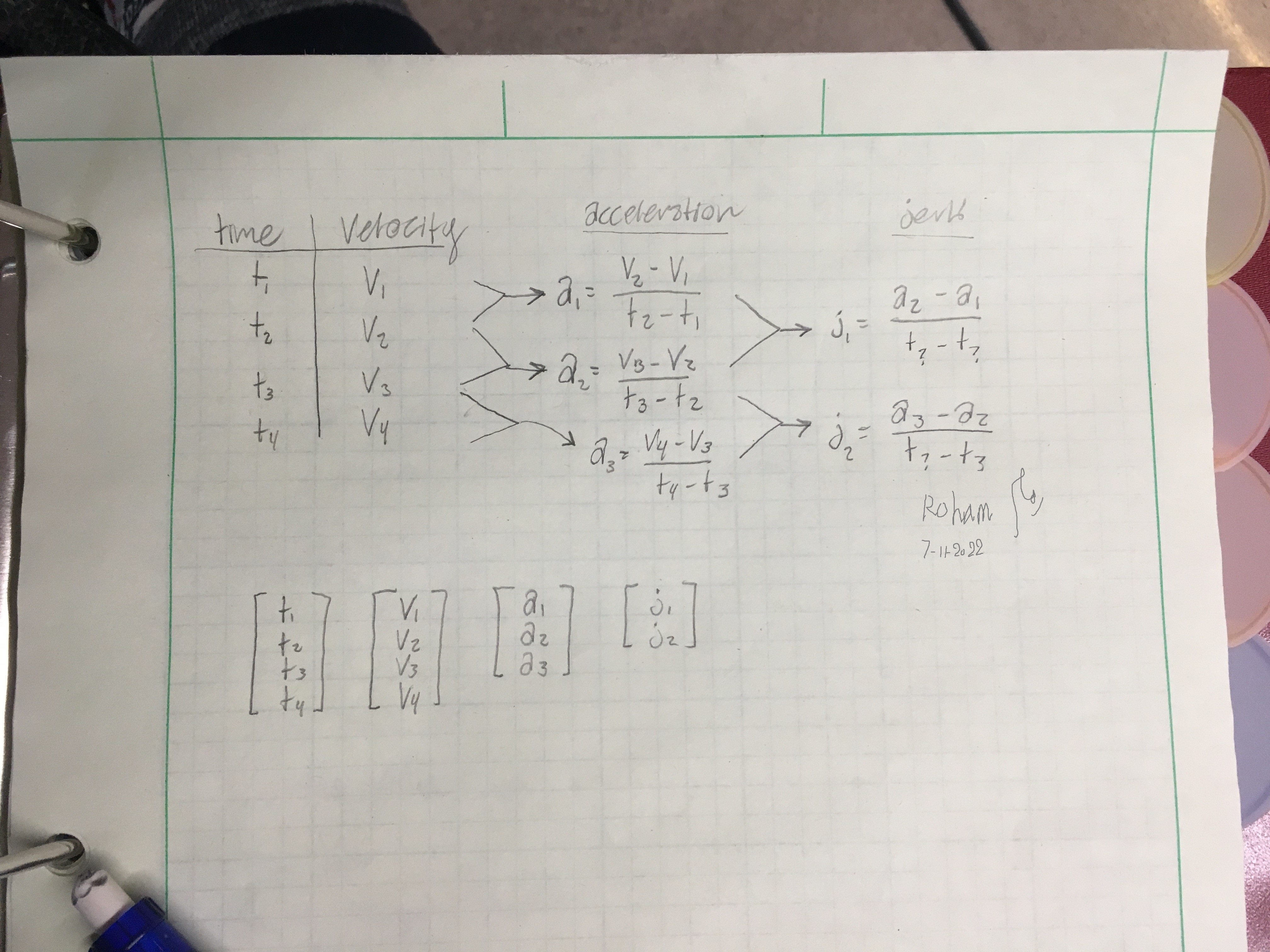
کلمه انگلیسی "jerk" در فیزیک برای اشاره به مشتق شتاب یعنی سومین مشتق موقعیت نسبت به زمان انتخاب شده است.
به عنوان مثال، ذره ای که موقعیت آن در زمان t ثانیه$x(t)=t^3$ متر است دارای سرعت$\displaystyle v(t) = \frac{dx}{dt}=3t^2$ متر بر ثانیه، شتاب$\displaystyle a(t) = \frac{dv}{dt}=6t$ متر در مجدورثانیه و a ثابت "جرک"$\displaystyle j = \frac{da}{dt}=6$متر در مکعب ثانیه.
به عنوان یک بردار، jerk j را می توان به عنوان اولین مشتق شتاب، مشتق زمان دوم سرعت، و مشتق سوم زمان از موقعیت بیان کرد:
${\displaystyle \mathbf {j} (t)={\frac {\mathrm {d} \mathbf {a} (t)}{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}\mathbf {v} (t)}{\mathrm {d} t^{2}}}={\frac {\mathrm {d} ^{3}\mathbf {r} (t)}{\mathrm {d} t^{3}}}}$
جایی که
a شتاب است
v سرعت است
r موقعیت است
زمان است
معدلات دیفرانسیل مرتبه سوم فرم
${\displaystyle J\left({\overset {\mathbf {...} }{x}},{\ddot {x}},{\dot {x}},x\right)=0}$گاهی اوقات معادلات تند و سریع نامیده می شوند. هنگامی که به یک سیستم معادل از سه معادله دیفرانسیل غیر خطی مرتبه اول معمولی تبدیل می شود، معادلات تند و سریع حداقل تنظیم برای راه حل هایی هستند که رفتار آشفته را نشان می دهند. این شرایط باعث ایجاد علاقه ریاضی در سیستم های تند و سریع می شود. سیستمهایی که مشتقهای مرتبه چهارم یا بالاتر را شامل میشوند، سیستمهای hyperjerk نامیده میشوند
احساس فشار دادن به صندلی ها در یک ماشین اسپرت پرقدرت به دلیل شتاب است. همانطور که ماشین از حالت سکون پرتاب می شود، یک حرکت مثبت بزرگ وجود دارد زیرا شتاب آن به سرعت افزایش می یابد. پس از پرتاب، یک تکان منفی کوچک و پایدار وجود دارد زیرا نیروی مقاومت هوا با افزایش سرعت خودرو افزایش مییابد، به تدریج شتاب کاهش مییابد و نیرویی که مسافر را به صندلی فشار میدهد کاهش مییابد. هنگامی که خودرو به حداکثر سرعت خود می رسد، شتاب به 0 رسیده و ثابت می ماند و پس از آن تا زمانی که راننده سرعت خود را کاهش دهد یا تغییر جهت دهد، هیچ حرکتی وجود ندارد.
هنگام ترمز ناگهانی یا در هنگام برخورد، مسافران با شتاب اولیه بیشتر از بقیه مراحل ترمز به جلو حرکت می کنند، زیرا تنش عضلانی پس از شروع ترمز یا ضربه سریعاً کنترل بدن را به دست می آورد. این اثرات در تست خودرو مدلسازی نمیشوند زیرا جسدها و آدمکهای تست تصادف کنترل فعال ماهیچهای ندارند.
برای به حداقل رساندن اثرات تند و تند، پیچهای کنار جادهها مانند پیچهای راهآهن و حلقههای ترن هوایی بهصورت کلوتوئیدی طراحی شدهاند.
نیرو، شتاب و حرکت تند
برای جرم ثابت m، شتاب a با نیروی F مطابق قانون دوم حرکت نیوتن نسبت مستقیم دارد:در چرخش
نمودار زمانبندی بیش از یک دور برای زاویه، سرعت زاویهای، شتاب زاویهای و تکانهای زاویهای
یک جسم صلب را در نظر بگیرید که حول یک محور ثابت در یک قاب مرجع اینرسی می چرخد. اگر موقعیت زاویه ای آن به عنوان تابعی از زمان θ(t) باشد، سرعت زاویه ای، شتاب و تکان را می توان به صورت زیر بیان کرد:
سرعت زاویه ای، ${\displaystyle \omega (t)={\dot {\theta }}(t)={\frac {\mathrm {d} \theta (t)}{\mathrm {d} t}}}$
حرکت تند زاویه ای، ${\displaystyle \alpha (t)={\dot {\omega }}(t)={\frac {\mathrm {d} \omega (t)}{\mathrm {d} t}}}$
,${\displaystyle \zeta (t)={\dot {\alpha }}(t)={\ddot {\omega }}(t)={\overset {...}{\theta }}(t)}$
شتاب زاویه ای برابر است با گشتاور اعمال شده روی بدنه تقسیم بر ممان اینرسی بدنه نسبت به محور لحظه ای چرخش. تغییر در گشتاور منجر به حرکت زاویه ای می شود.
حالت کلی یک جسم صلب در حال چرخش را می توان با استفاده از نظریه پیچ سینماتیکی، که شامل یک بردار محوری، سرعت زاویه ای Ω(t) و یک بردار قطبی، سرعت خطی v(t) مدل سازی کرد. از این رو، شتاب زاویه ای به صورت تعریف می شود
${\displaystyle {\boldsymbol {\alpha }}(t)={\frac {\mathrm {d} }{\mathrm {d} t}}{\boldsymbol {\Omega }}(t)={\dot {\boldsymbol {\Omega }}}(t)}$و حرکت تند و سریع زاویه ای توسط داده می شود
${\displaystyle {\boldsymbol {\zeta }}(t)={\frac {\mathrm {d} }{\mathrm {d} t}}{\boldsymbol {\alpha }}(t)={\dot {\boldsymbol {\alpha }}}(t)={\ddot {\boldsymbol {\Omega }}}(t)}$
به عنوان مثال، درایو ژنو را در نظر بگیرید، دستگاهی که برای ایجاد چرخش متناوب یک چرخ چرخ و با چرخش مداوم چرخ محرک استفاده می شود. در طول یک چرخه چرخ محرک، موقعیت زاویه ای چرخ رانده θ 90 درجه تغییر می کند و سپس ثابت می ماند. به دلیل ضخامت محدود چنگال چرخ محرک (شیار پین محرک)، این دستگاه یک ناپیوستگی در شتاب زاویه ای α و یک حرکت تند زاویه ای نامحدود ζ در چرخ رانده ایجاد می کند.
یک مارپیچ اویلر، از لحاظ نظری منحنی گذار بهینه، شتاب مرکز را به صورت خطی افزایش میدهد و منجر به تکانهای ثابت میشود (نمودار را ببینید). در کاربردهای دنیای واقعی، صفحه مسیر در امتداد بخشهای منحنی متمایل است. شیب باعث شتاب عمودی می شود که یکی از ملاحظات طراحی برای سایش در مسیر و خاکریز است. Wiener Kurve (منحنی وینی) یک منحنی ثبت شده است که برای به حداقل رساندن این سایش طراحی شده است
ترن هوایی همچنین با انتقال مسیر برای محدود کردن حرکت تند و سریع طراحی شده است. هنگام ورود به یک حلقه، مقادیر شتاب می تواند به حدود 4 g (40 متر بر ثانیه) برسد و سواری در این محیط با شتاب بالا فقط با انتقال مسیر امکان پذیر است. منحنی های S شکل، مانند شکل هشت، همچنین از انتقال مسیر برای سواری نرم استفاده می کنند.
مشتقات بالاتر (تحرک، پرش) موقعیت با توجه به زمان چگونه در فیزیک استفاده می شود
تعمیم یک مفهوم یکی از چیزهایی است که مردم معمولاً به آن نگاه می کنند تا دید بزرگ تری از یک ایده داشته باشند. بنابراین یکی از چیزهای طبیعی که باید در مورد آن تعجب کنید وقتی اینجا هستید که اگر سرعت مشتق زمانی موقعیت و شتاب مشتق زمانی سرعت است،
ترن هوایی یک مثالش
از آنجایی که معادلات حرکت مرتبه دوم هستند، مشتقات بالاتر هیچ اطلاعات جدیدی نمی دهند (اما به طور منحصر به فرد از شرایط اولیه موقعیت و سرعت پیروی می کنند)، بنابراین معمولاً مورد بحث قرار نمی گیرند.
مشتقات بالاتر در برخی از کاربردهای مهندسی، از آنجایی که حرکت حرکتی سرعت تغییر شتاب را تعیین می کند، زمانی که برخی از وسایل مکانیکی باید با نیروی ظاهری ناشی از شتاب وارد تعادل شوند، مهم است. به طور شهودی، اگر حرکت تند و سریع به نحوی بالاتر از فرکانس رزونانس باشد، ممکن است اتفاقات ناخوشایندی رخ دهد (زیرا به جای یافتن یک تعادل جدید، سیستم در عوض نوسان می کند و ممکن است شکسته شود).
این موضوع برای سیستمهای کنترلشده (مانند انسانها) که ممکن است در یک حرکت بزرگ شکسته شود، اهمیت بیشتری پیدا میکند (زیرا اگر نقطه تنظیم به سرعت تغییر کند، زمان کافی برای رسیدن به یک حالت تعادل جدید ندارد). ویکی پدیا را در این مورد ببینید.
حرکت تند و سریع در یک مورد در فیزیک در یک معادله حرکت رخ می دهد: کاهش تابشی حرکت. نیروی لورنتس-ابراهام را ببینید. به نظر میرسد که این باعث ایجاد مشکلاتی در رابطه علیت و بقای انرژی میشود (زیرا معادله راهحلی با انرژی بینهایت افزایش میدهد، اگر حرکت حرکتی اولیه ویژگیهای خاصی داشته باشد). در یک سیستم فیزیکی از این مشکلات اجتناب می شود زیرا حرکت تند و سریع اولیه در واقع آزاد نیست، بلکه توسط حرکت قبلی سیستم محدود شده است. (این مشکل به دلیل چگالی انرژی بی نهایت بار نقطه ای به وجود می آید، بنابراین به طور مستقیم از ناهماهنگی الکترودینامیک کلاسیک - به دلیل نسبیت خاص، که از الکترودینامیک کلاسیک ناشی می شود، ذرات باید نقطه مانند باشند، اما الکترودینامیک کلاسیک واگرایی هایی را نشان می دهد. هزینه های امتیازی).
در دنیای F=mv، تکانه و نیرو معادل هستند. یک جسم را به سختی فشار دهید، و بلافاصله شروع به حرکت می کند. اگر گرانش به عنوان یک نیرو عمل کند (اگر سناریوی کمی متفاوت بخواهیم باز هم می تواند یک شتاب باشد) آنگاه هر چیزی که نزدیک به یک جرم است به سمت آن حرکت می کند و به سمت چگالی های بالاتر منفجر می شود تا زمانی که فشار گرانش را متعادل کند. هیچ مداری وجود نخواهد داشت زیرا سرعت ها مستقیماً روی جرم اصلی قرار می گیرند. یک توپ رها شده از معادله x′(t)=−g پیروی می کند، یعنی x(t)=−gt+x(0): اجسام با سرعت ثابت سقوط می کنند - در واقع، وقتی توپی را پرتاب می کنید، به محض اینکه از دست شما خارج می شود و سرعت را به سرعت جاذبه تغییر می دهد.
در دنیای F=mj، شتاب ها بسیار ملایم تر خواهند بود. شما باید چیزی را بیشتر فشار دهید تا حرکت کند. یک توپ پرتاب شده از معادله x′′′(t)=−g پیروی می کند، یعنی $x(t)=-(1/6)g t^3 + a_0 t^2 + v_0t + x(0)$: اگر از حالت سکون خارج شود، طول می کشد. زمان بیشتری برای کاهش آن وجود دارد اما سرعت حتی سریعتر رشد می کند. احتمالاً ردی از شتابی که به آن دادید نیز باقی میماند: آن را محکم به سمت بالا پرتاب کنید، و نه تنها بالا میآید، بلکه برای مدتی به شتاب ادامه میدهد تا زمانی که گرانش از بین برود.
به طور کلی، می توان این بازی را بازی کرد (که سرگرم کننده است)، اما مشکل اصلی اگر از نظر ریاضی منطقی باشد. ساختار مکانیک کلاسیک نوعی نردبان است که در آن جفتهای نیرو-شتاب، تکانه-سرعت و انرژی-موقعیت به روشی درست به هم متصل میشوند و چیزهای مهمی مانند قوانین بقای تولید میکنند. این سناریوهای دیگر اساساً باید تمام فیزیک را یک پله بالا یا پایین ببرند. به این ترتیب احتمالاً میتوان لاگرانژیان و همیلتونها را به روشی معادل برای سناریوها تعریف کرد، دینامیک بسیار متفاوت و کمیتهای حفظشده را دریافت کرد، اما اساساً ساختار را ثابت نگه داشت.شتاب با نیرو تغییر می کند، بنابراین مشتق شتاب با مشتق نیرو تغییر می کند. به عبارت دیگر، اگر،
$m\ddot x = F,$
سپس،
$m\dddot x = \dot F.$
بنابراین، تند و سریع، سرعتی است که در آن نیرو در حال تغییر است، تقسیم بر جرم جسم. اگر جسمی را تکان دهید، به طور خلاصه نیروی وارد شده را از صفر به عددی تغییر می دهید، و هر چه مدت زمانی که آن را از بی نیرو به نیروی کامل برسانید، کوتاه تر است، «تحرک» عمل بیشتر می شود.نحوه محاسبه حرکت حرکتی که یک جسم را به سرعت معینی می رساند
مشکل من خیلی ساده به نظر می رسد، اما نمی توانم پاسخی پیدا کنم:
من یک جسم با سرعت مشخص v0 و شتاب a0 دارم. هدف من در زمان T سرعت جدید vx و شتاب صفر است.
چگونه می توانم تابعی را در طول زمان محاسبه کنم، که برای رسیدن به این هدف، تکان ثابت مثبت یا منفی فعلی (مشتق شتاب) را به من می دهد؟
برای مثال در دنیای واقعی، سرعت دست خود را روی دریچه گاز در نظر بگیرید. اگر موتور موشک شما نیروی رانشی متناسب با موقعیت دریچه گاز ایجاد کند، سرعت دست شما متناسب با حرکتی است که مسافران شما تجربه خواهند کرد.
یکی دیگر از کمک های شهودی ممکن است فکر کردن در مورد شتاب بر حسب گرانشی باشد که معادل آن است. اگر مسافر موشک یا آسانسور هستید و احساس میکنید وزنتان به طور ناگهانی دو برابر میشود، تند تند است. اگر وزن شما به آهستگی در حال افزایش یا کاهش است، کاهش وزن است. این به این دلیل است که وزنی که احساس می کنید متناسب با شتاب شما بالا و پایین می شود.تند و سریع (آن را j می نامیم) سومین مشتق موقعیت است. معادله معمول شما$x(t)=x_0+v_0t+\frac 12a_0t^2$ یک عبارت$\frac 1{3!}j_0t^3$اضافه می کند. می توانید از مشتقات برای دادن v(t) و a(t) استفاده کنید و سپس از نقاط شناخته شده خود برای ارزیابی پارامترها استفاده کنید. شما یک محدودیت بیش از حد دارید. شما می توانید حرکت تند را از اختلاف شتاب ها تقسیم بر زمان محاسبه کنید، اما هیچ تضمینی وجود ندارد که بتوانید تغییر سرعت مورد نظر خود را برآورده کنید.

کلمه انگلیسی "jerk" در فیزیک برای اشاره به مشتق شتاب یعنی سومین مشتق موقعیت نسبت به زمان انتخاب شده است.
به عنوان مثال، ذره ای که موقعیت آن در زمان t ثانیه$x(t)=t^3$ متر است دارای سرعت$\displaystyle v(t) = \frac{dx}{dt}=3t^2$ متر بر ثانیه، شتاب$\displaystyle a(t) = \frac{dv}{dt}=6t$ متر در مجدورثانیه و a ثابت "جرک"$\displaystyle j = \frac{da}{dt}=6$متر در مکعب ثانیه.

- MRT
نام: محمدرضا طباطبایی
محل اقامت: تبریز
عضویت : پنجشنبه ۱۳۸۶/۴/۲۱ - ۱۸:۱۷
پست: 2415-
سپاس: 95
- جنسیت:
تماس:
Re: سوال : مشتق شتاب
مشتق معادله یا منحنی شتاب به چی؟ نسبت به زمان یا فاصله یا سرعت؟
با توجه به ماده 8 قوانین تالار گفتمان شبكه فیزیك هوپا :
ارايه انديشههاي نو در فيزيك و متافيزيك ، رياضيات مختص فيزيك ، حساب و هندسه دوجيني در وب سايت شخصي :
https://ki2100.com

ارايه انديشههاي نو در فيزيك و متافيزيك ، رياضيات مختص فيزيك ، حساب و هندسه دوجيني در وب سايت شخصي :
https://ki2100.com


- MRT
نام: محمدرضا طباطبایی
محل اقامت: تبریز
عضویت : پنجشنبه ۱۳۸۶/۴/۲۱ - ۱۸:۱۷
پست: 2415-
سپاس: 95
- جنسیت:
تماس:
Re: سوال : مشتق شتاب
نسبت به فاصله میشه یک تقسیم بر مربع زمان
نسبت به زمان میشه منهای دو فاصله تقسیم بر مکعب زمان
نسبت به سرعت میشه یک تقسیم بر زمان
نسبت به زمان میشه منهای دو فاصله تقسیم بر مکعب زمان
نسبت به سرعت میشه یک تقسیم بر زمان
با توجه به ماده 8 قوانین تالار گفتمان شبكه فیزیك هوپا :
ارايه انديشههاي نو در فيزيك و متافيزيك ، رياضيات مختص فيزيك ، حساب و هندسه دوجيني در وب سايت شخصي :
https://ki2100.com


ارايه انديشههاي نو در فيزيك و متافيزيك ، رياضيات مختص فيزيك ، حساب و هندسه دوجيني در وب سايت شخصي :
https://ki2100.com