گشتاور مغناطیسی
تکانه زاویه ای یا گشتاور زاویه ای از رابطه $L=r\times p$ به دست می آید.
در صورتی که یک الکترون دارای تکانه زاویه ای باشد با توجه به روابط کلاسیک باید دارای میدان الکترومغناطیس باشد و مثل یک آهنربای کوچک، گشتاور مغناطیسی یا دو قطبی مغناطیسی ایجاد کند.
رفتار دو قطبی در میدان مغناطیسی
اگر یک گشتاور مغناطیسی در یک میدان مغناطیسی یکنواخت قرار بگیرد بر اساس زاویه بردار مغناطیسی که در آن قرار گرفته است تغییر جهت میدهد. بعنوان مثال قرار دادن یک آهنربا که یک دوقطبی مغناطیسی است در میدان زمین باعث جهت گیری قطبهای آن به سمت شمال و جنوب میشود. در این حالت نیروهای وارده به دو سمت 2 قطبی بر خلاف یکدیگر بوده و برابر هستند. این نیروها یکدیگر را خنثی نموده و در نتیجه دو قطبی تنها دارای تغییر جهت خواهد بود.
در صورتی که یک میدان مغناطیسی غیریکنواخت را فرض کنیم میدانی که میتواند بعنوان مثال افزایش چگالی شار مغناطیسی همانند شکل از پایین به بالا باشد رفتار ذره با گشتاور مغناطیسی در آن متفاوت از میدان یکنواخت خواهد بود.
$$F_{z}= \frac{\partial}{\partial z}(\mu .B)\simeq \mu_{z}\frac{\partial B_{z}}{\partial z}$$
در این صورت علاوه بر جهت گیری همانند میدان یکنواخت، به علت تفاوت در چگالی شار در دو سمت دو قطبی نیروهای متفاوتی به دو سمت دو قطبی وارد میشود و محاسبه برایند نیروهای وارده اعمال نیرو به یک سمت را نتیجه خواهد داد.
بنابر این به طور کلی قرار گیری دو قطبی در میدان مغناطیسی غیر یکنواخت توزیع شده در فضا، باعث اعمال نیرو به دو قطبی مغناطیسی می شود.
اندازه گیری گشتاور مغناطیسی ذره
در آزمایش اشترن گرلاخ با وارد کردن ذرات به درون میدان مغناطیسی غیر یکنواخت و اندازه گیری میزان انحراف ذره پس از خروج از میدان مغناطیسی، میتوان به یک اندازه متناسب با گشتاور مغناطیسی الکترون رسید. میزان نیروی وارده به هر دو قطبی و در نتیجه میزان انحراف ذره پس از خروج نشان دهنده میزان گشتاور مغناطیسی ذره خواهد بود.

در صورتی که بخواهیم تنها یک الکترون را به درون میدان پرتاب کنیم به علت اعمال نیروی لورنتز ذره نیروهای دیگری غیر از نیروی ناشی از حضور در میدان غیر یک نواخت تجربه میکند.
برای جلوگیری و حذف این گونه نیروها و جهت جلوگیری از تداخل آنها با نیروی وارده به گشتاور مغناطیسی باید از یک اتم که به طور کلی بار الکتریکی آن خنثی است به درون میدان پرتاب شود.
در ازمایش اشترن گرلاخ از اتم های نقره استفاده شده است. در اتم نقره الکترون های لایه های زیرین به صورت جفت شده می باشند و گشتاورهای همدیگر را خنثی میکنند. تنها الکترون باقی مانده لایه آخر است که به صورت جفت نشده است. همچنین اینکه بار کلی اتم از نظر الکتریکی خنثی می باشد در نتیجه نیروی لورنتز وجود نخواهد داشت. با توجه به اینکه این الکترون به صورت ابری موج گونه در تمامی اطراف اتم احاطه شده است، پرتاب اتم نقره به داخل میدان مغناطیسی در حقیقت اندازه گیری گشتاور زاویه ای الکترون لایه آخر یا به عبارتی اندازه گیری گشتاور زاویه ای الکترون است.
اگر اتم ها به درون میدان پرتاپ شوند پس از جهت گیری به علت تفاوت در میزان گشتاورهای یکدیگر باید خود را به صورت توزیعی از برخورد ذرات اتم نقره در خروجی نشان دهند.
بررسی مشاهدات
مشاهداتی که از نتیجه برخورد اتم های خروجی به سطح برخورد حاصل شد بر خلاف انتظار بود و توزیع برخورد الکترون ها به صفحه به جای یک توزیع نرمال، یک توزیع دو قسمتی بالا و پایین را شکل داد.
این موضوع باعث شد که اندازه اسپین الکترون به صورت کمیتی گسسته یا کوانتومی اندازه گیری شود.
فروپاشی تابع موج اسپین
با توجه به کوانتومی بودن اسپین الکترون، میتوان به آن یک موج نسبت داد. این موج در حالت اندازه گیری نشده در حالتی از برهم نهی حالت های پایه خود است.
پس از اندازه گیری، تابع موج اسپین به صورتی که اندازه گیری شده فرو می پاشد. با گذر زمان رفته رفته تابع اسپین مجدد به حالت قبل باز میگردد. زیرا توابع موج در مکانیک کوانتومی توسط یک انتشارگر بر حسب زمان در حال تحول هستند.
هنگامی که آزمایش تلاش کند میزان اسپین را در جهت x اندازه گیری کند تابع اسپین در این جهت در یکی از مقادیر مثبت یا منفی فرو می پاشد.
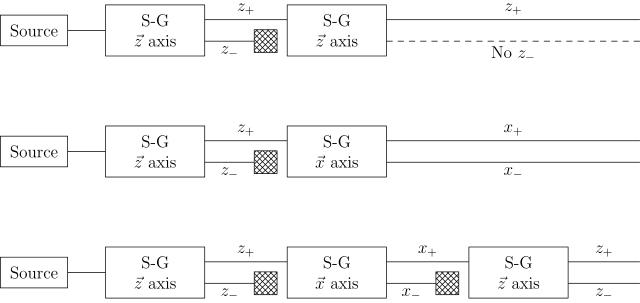
در این حالت ابتدا جهت اسپین ذره در جهت z اندازه گیری میشود. سپس Z down مسدود شده و خروجی Z up بلافاصله در جهت Z اندازه گیری شود. خروجی این حالت فقط دارای یک حالت و برابر با Zup می باشد.
حالت دوم:
در این حالت ابتدا جهت اسپین ذره در جهت Z اندازه گیری میشود. سپس Z down مسدود شده و خروجی Z up بلافاصله در جهت X اندازه گیری میشود. خروجی این حالت دارای 2 حالت X up و X down می باشد.
حالت سوم:
در این حالت ابتدا جهت اسپین ذره در جهت z اندازه گیری میشود. سپس Z down مسدود شده و خروجی Z up بلافاصله در جهت X اندازه گیری میشود. سپس X down مسدود شده و X up بلافاصله به یک آزمایش در جهت اندازه گیری اسپین Z وارد میشود. خروجی در این حالت دارای 2 حالت تصادفی Z up و Z down میباشد.
ملاحظه میشود که در حالت سوم با وجود اینکه قبلا ذره در حالت Z up جایگزیده شده، اما به دلیل اندازه گیری در جهت X در صورت آزمایش مجدد در جهت Z مجددا دارای اسپین بالا و پایین خواهد بود. این موضوع نشانگر این است که با اندازه گیری اسپین ذره در یک جهت اطلاعات اسپین در جهت دیگر از بین خواهد رفت.
به عبارت دیگر با اندازه گیری اسپین به طور دقیق در یک محور، اطلاعات اندازه گیری در محور دیگر از دست خواهد رفت. اصلی که به شکلی به اصل عدم قطعیت اشاره دارد.
علت حضور Zd مسدود شده در خروجی حالت سوم
Zup را با Zu و Zdown را با Zd نمایش میدهیم و به همین ترتیب در مورد X و Y عمل میکنیم.
چرا با وجود اینکه در حالت سوم، حالت Zd مسدود شده است مجددا در خروجی Zd ظاهر میشود؟
برای پاسخ به این پرسش این سیستم را با عبور نور از قطبش گر ها مورد مقایسه قرار میدهیم. در این مقایسه دیدگاه کلاسیکی الکترومغناطیس را در عبور از قطبش گر ها بررسی میکنیم. میتوانیم این مقایسه را نسبت به فوتون از دیدگاه کوانتومی و با بررسی احتمال حضور فوتون ها با اسپین چرخشی اندازه بگیریم اما دیدگاه کلاسیک در اینجا کفایت میکند.
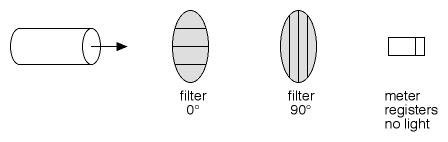
ابتدا نور را از یک قطبش گر x عبور میدهیم. در نتیجه قطبش y حذف میشود و قطبش x عبور میکند.
سپس نور را از یک قطبش گر y عبور میدهیم. در نتیجه قطبش x حذف میشود و قطبش y عبور میکند و چون قطبش y قبلا حذف شده در خروجی هیچ نوری نخواهیم داشت.
شباهت این آزمایش با آزمایش اسپین در این است که همانگونه که در حالت سوم Zd مسدود شد اما در خروجی ظاهر شد، در این آزمایش با 3 قطبش گر نیز با وجود حذف y پس از فیلتر اول، در انتها این محور y است که از قطبشگر سوم خارج میشود. همچنین قطبشگر در زاویه 45 درجه با اندازه گیری اسپین در جهت x مشابهت دارد.
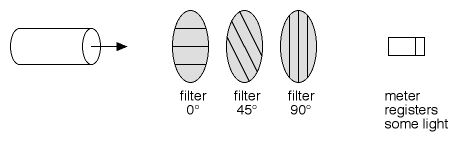
پس از عبور از قطبش گر وسط مجددا بردار فعلی را به پایه های فیلتر آخر تجزیه میکنیم که یکی عبور کرده و دیگری مسدود میشود.

سپس حالت $x$ عبور شده بر پایه های قطبشگر 45 درجه بر حالت های $\acute{\hat{x}}$ و $\acute{\hat{y}}$ تجزیه میکنیم(مقدار حالت برابر با $\acute{\hat{x}}-\acute{\hat{y}}$).
سپس از قطبشگر دوم حالت $\acute{\hat{x}}$ عبور میکند .
حالت خروجی $\acute{\hat{x}}$ قبل از عبور از قطبشگر سوم به پایه های قطبشگر سوم یعنی $x$ و $y$ تجزیه میشود.
حالت $y$ در خروجی قرار میگیرد.
فرمول بندی روابط ریاضی شدت و معادلات حالت
میخواهیم رابطه اسپین Zu را در شکل بالا حالت اول در خروجی اندازه گیری بنویسیم.
میتوانیم از یک فرمول کلی تر حالت اول با زاویه صفر درجه و حالت دوم با زاویه 90 درجه و هر حالت دیگر با زاویه متفاوت را محاسبه کنیم در این حالت از فرمول زیر استفاده میکنیم:
$$\psi (\theta )= cos(\theta/2)Z_{u} + sin(\theta/2)Z_{d}$$
همانطور که گفته شد اگر بلافاصله پس از خروج الکترون با اسپین Zu دوباره آن را در جهت Z اندازه بگیریم با احتمال 100 درصد Zu در خروجی اندازه گیری میشود. چون تتا میزان زاویه انحراف از Z است و اندازه گیری دقیقا در همان محور Z اندازه گرفته شده بنابر این تتا برابر با صفر می باشد.
با قرار دادن مقدار تتا در رابطه برابر با صفر و محاسبه اندازه موج برابر با 1 به دست می آید.
$$P_{u}= cos^{2}(\theta/2)= cos^{2}(0)=1$$
بعنوان مثال اگر اندازه گیری با یک زاویه 90 درجه صورت بگیرد، در این صورت احتمال Pu در خروجی 50 درصد خواهد بود. در این حالت به ازمایشی شبیه به شکل دوم میرسیم. چون در این حالت در واقع اندازه گیری در حالت X در حال اندازه گیری است و 2 خروجی Xu و Xd داریم در این صورت میزان Xu را محاسبه میکنیم.
با قرار دادن تتا برابر با 90 درجه داریم:
$$X_{u}= cos(\theta/2)Z_{u} + sin(\theta/2)Z_{d} $$
$$X_{u}= (Z_{u} +Z_{d})\frac{\sqrt{2}}{2}$$
چون Xd همان Xu درحالتی است که آزمایشگر 180 درجه چرخیده است بنابر این میتوان Xd را نیز به این صورت نوشت
$$X_{d}= cos(\theta/2)Z_{u} - sin(\theta/2)Z_{d}$$
$$X_{d}=(Z_{u} -Z_{d})\frac{\sqrt{2}}{2} $$
به طریق مشابه میتوان با جمع طرفین 2 رابطه بالا و ضرب در $\frac{\sqrt{2}}{2}$ به روابط زیر رسید:
$$Z_{u}= (X_{u} +X_{d})\frac{\sqrt{2}}{2} $$
$$Z_{d}= (X_{u} -X_{d})\frac{\sqrt{2}}{2} $$
بنابر این گرچه در حالت دوم، اندازه گیری در جهت x انجام شده است و Xd مسدود شده و خروجی Xu در حال محاسبه است اما این مقدار هنوز میتواند توسط پایه های Zu و Zd نوشته شود. همینطور به طریقی مشابه Zu و Zd نیز بر حسب Xu و Xd نوشته شدند.
محاسبه مقدار Yu و Yd
اگرچه در اینجا چرخش 90 درجه ای توانست روابط محورهای x و z را محاسبه کند اما محور y نمی تواند به این صورت نوشته شده یا به دست آید.
برای محاسبه y میتوانیم با توجه به تقارن، فرض کنیم اسپین y در حالتی که اسپین z به سمت محور x در حال حرکت است، مشابه است با اسپین x وقتی اسپین z به سمت محور y در حرکت است.
بنابر این اسپین y نیز همانند اسپین x باید ترکیب خطی از حالت های پایه Zu و Zd باشد.
اگر با شرایط فعلی بخواهیم محور y را نیز همانند محور x با ترکیب خطی از حالت های Zu و Zd بنویسیم به علت تشابه روابط تفکیکی بین روابط x و y نمی بینیم. درحالیکه باید روابط x و y که هردو از جمع برداری حالت های Zu و Zd هستند از همدیگر قابل تفکیک باشند.
این موضوع ثابت میکند که روابط ریاضیاتی اسپین x و اسپین y کامل نیستند یا می توانند به طریقی تعمیم داده شوند. با توجه به اینکه تابع موج اسپین یک تابع درحال تحول زمانی و فرکانسی مشخص است زمان میتواند یکی از این عوامل باشد که به صورت اختلاف فاز اعمال شده نمایش داده میشود.
برای محاسبه Yu و Yd مجددا از اپتیک و تشابه بین روابط اسپین و آزمایش اپتیکی کمک می گیریم.
این بار از یک quarter wave plate استفاده میکنیم. رفتار این ماده نسبت به قطبش های مختلف متفاوت است. بعنوان مثال یکی از قطبش های x و y میتواند با تاخیر 90 درجه فاز از آن خارج شود. ترکیب خطی میدان ها با فاز صفر و 90 درجه ایجاد قطبش چرخشی یا circularly polarized light را نتیجه میدهد.
$$E=E_{0}\left[\frac{1}{\sqrt{2}}\hat{x}Cos(kz-wt)+\frac{1}{\sqrt{2}}\hat{y}Cos(kz-wt+\frac{\pi}{2})\right]$$
برای سهولت در محاسبات، تابع موج نور را به جای استفاده از شکل های مثلثاتی همانند $E_{0}.Sin(kz-wt)$ به صورت نمایی $e^{i(kz-wt)}$ مینویسیم و تعریف میکنیم که قسمت حقیقی تابع نمایی برابر با میدان الکتریکی مورد نظر ما می باشد که با تقسیم بر $E_{0}$ نرمالیزه شده است.
$$Re(\epsilon)=E/E_{0}$$
به ازای این تعریف که برای سهولت در محاسبات است تاخیر فاز را نیز به صورت $e^{i\frac{\pi}{2}}=i$ می نویسیم .
$$\epsilon=\left[\frac{1}{\sqrt{2}} e^{i(kz-wt)} + \frac{i}{\sqrt{2}} e^{i(kz-wt)} \right]=(1+i)\frac{1}{\sqrt{2}}e^{i(kz-wt)} $$
اگر یک نور قطبیده در جهت x را به یک تاخیر ربع فاز که به صورت 45 درجه نصب شده است عبور دهیم، نور قطبیده در جهت ایکس به دو مولفه $\acute{x}$ و $\acute{y}$ تجزیه میکنیم که یکی از اینها با تاخیر ربع فاز و دیگری بدون تاخیر ظاهر شده با ترکیب خطی آنها یک موج با قطبش چرخشی بوجود می آید که با عبور از هر یک از قطبش گر های x یا y به طور جداگانه در هر دو حالت دارای خروجی با شدت برابر هستیم.
برای مثال ابتدا قطبش y را حذف میکنیم. سپس به عملگر quarter wave plate با زاویه 45 درجه اعمال میکنیم. موج با قطبش چرخشی خارج شده را به قطبشگر y داده و x را حذف میکنیم. در نتیجه خروجی دارای قطبش y می باشد. قطبشی که از فیلتر اول حذف شده بود اما در خروجی ظاهر گردید. این موضوع نشان میدهد که عملگر تاخیر ربع فاز همانند نوعی اندازه گیری اسپین می باشد.
همانطور که قطبشگر 45 درجه میان دو قطبشگر x و y در آزمایش اول شبیه به عملگر اندازه گیری اسپین در جهت x بود در اینجا عامل تاخیرفاز با زاویه 45 درجه میان دو قطبشگر شبیه به اندازه گیری در اسپین y است.
بنابر این با مشابهت دادن quarter wave plate در زاویه 45 درجه به عملگر اندازه گیری اسپین y میتوانیم Yu را با نور قطبیده چرخشی راست گرد و Yd را با نور قطبیده چپ گرد تشبیه کنیم.
بنابر این میتوانیم روابط Yu و Yd را به صورت زیر بنویسیم:
$$Y_{u}= (Z_{u} +iZ_{d})\frac{\sqrt{2}}{2}$$
$$Y_{d}= (Z_{u} -iZ_{d})\frac{\sqrt{2}}{2}$$
توجه شود که انتخاب i کنار بخش دوم قراردادی است و میتوان هردوی بخش هارا مختلط نوشت به گونه ای که فاز کل 90 درجه باشد.
این حدس یعنی مختلط بودن بخش های y که از طریق اپتیک محاسبه گردید در ادامه صحت سنجی خواهد شد.
علت مختلط بودن ضرائب
همانطور که اشاره شد ضرائب مختلط تنها به جهت محاسبه فاز ترم مختلط نمایی بوده و انتخاب ترم نمایی نیز به جهت سهولت در محاسبات بوده و در نهایت اسپین یا میدان نهایی مقدار حقیقی ترم نمایی ضربدر ضریب مورد نظر می باشد.
نوتیشن دیراک
بردارهای پایه میتوانند در پایه های مختلف به صورت های مختلف نوشته شوند. بعنوان مثال $\begin{bmatrix}1 \\0\end{bmatrix}$ می تواند در پایه برداری دیگر به صورت $\begin{bmatrix}\frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2}\end{bmatrix}$ یا به شکل کلی تری $\begin{bmatrix}sin(\theta) \\ cos(\theta)\end{bmatrix}$نوشته شود درحالیکه هردو اندازه واحد دارند.
بنابر این با انتخاب بردارهای پایه Zu و Zd در ادامه Zu را با $\begin{bmatrix}1 \\0\end{bmatrix}$ و Zd را با $\begin{bmatrix}0 \\1\end{bmatrix}$ نمایش میدهیم. 2 برداری که با هم دیگر متعامد هستند.
جهت استفاده کوتاه تر و فشرده تر از نوتیشن دیراک استفاده میکنیم که مزایای مختلفی دارد. در نوتیشن دیراک بردارهای ستونی به صورت کت نمایش داده میشوند و بردارهای سطری با برا bra با درایه های مزدوج شده نمایش داده میشوند.
ضرب یک سطر در ستون به صورت ضرب داخلی یک bra و یک ket نمایش داده میشود. اگر بخواهیم یک برا را به کت تبدیل کنیم ماتریس سطری را به ستونی و درایه هارا مزدوج میکنیم.
پایه های برداری انتخابی را با کت های $|+\rangle$ و $|-\rangle$ نمایش میدهیم.
نمونه یک ضرب داخلی که نشان دهنده تعامد پایه ها می باشد به صورت براکت یا ضرب داخلی یک برا در کت : $\langle-|+\rangle$ و به معنای ضرب ماتریس $\begin{bmatrix}0 &1\end{bmatrix}\begin{bmatrix}1 \\0\end{bmatrix}=0$ می باشد.
خروجی براکت یا ضرب داخلی، یک عدد میباشد.
اکنون روابط قبل را در نوتیشن دیراک مینویسیم:
$$|S_{x};\pm\rangle=\frac{\sqrt{2}}{2}|S_{z};+\rangle\pm\frac{\sqrt{2}}{2}|S_{z};-\rangle$$
$$|S_{y};\pm\rangle=\frac{\sqrt{2}}{2}|S_{z};+\rangle\pm i\frac{\sqrt{2}}{2}|S_{z};-\rangle$$
اندازه گیری و ماتریس های عملگر
عمل اندازه گیری در مکانیک کوانتومی میتواند توسط یک ماتریس بیان شود. ماتریس های مربعی عملگر یا اپراتورها میتوانند بر روی حالت ورودی عمل کرده و حالت خروجی را به دست دهند.
بعنوان مثال وقتی یک اندازه گیری روی یک حالت انجام میشود، مقدار حالت ورودی تحت تاثیر اندازه گیری قرار می گیرد و تغییر میکند.
در اینجا اپراتور اندازه گیری یا ماتریس اندازه گیری مثلا اسپین X وقتی روی حالت ورودی عمل میکند میتواند حالت خروجی را مشخص کند.
به صورت ماتریسی عملا یک ماتریس مربعی nxn بر روی یک ماتریس ستونی nx1 یک ماتریس ستونی nx1 به دست میدهد. این ضرب در نوتیشن دیراک به صورت ضرب عملگر در یک کت باشد که کت خروجی نمایانگر حالت خروجی پس از اندازه گیری است.
در اینجا میتوانیم برای اندازه گیری اسپین های x,y,z سه عملگر مشخص کنیم. این کار توسط ترکیب اصول موضوعه مکانیک کوانتومی و مشاهدات صورت گرفته از آزمایش اشترن گرلاخ صورت میگیرد.
در اینجا حالت هایی شبیه به $|a\rangle |b\rangle$ غیر قانونی است.
اما حالت هایی شبیه به $|a\rangle \langle b|$ اگر بعنوان مثال سمت چپ یک کت یا راست یک برا قرار گیرد دارای کت یا برا در خروجی خواهد بود. مثلا حاصل $(|a\rangle \langle b|).|c\rangle$ که میتواند به صورت $|a\rangle \langle b|c\rangle$ نوشته شود؛ یک کت است که به 2 صورت قابل محاسبه است. اول اینکه $|a\rangle \langle b|$ محاسبه شود که بعنوان ضرب خارجی شناخته میشود. خروجی این ضرب یک ماتریس nxn است و همانند یک عملگر می باشد. سپس این عملگر برروی کت c عمل کند. حالت دوم ضرب داخلی b و c و سپس ضرب عدد حاصل در کت a است که هردو حالت یکسان هستند.
بنابر این عباراتی همچون $|a\rangle \langle b|$ عملگر هستند.
محاسبه عملگرها و به دست آوردن عملگرهای اسپین
در روابط پیشین حالت ها بر حسب یکدیگر نوشته شدند. در اینجا عملگر اندازه گیری $S_{z}$ را بر روی حالت $|S_{z};+\rangle$ اعمال میکنیم چون میدانیم بعد از اندازه گیری و اعمال عملگر روی حالت ورودی $|S_{z};+\rangle$ احتمال صد درصد حالت $|S_{z};+\rangle$ به دست می آید و حالت $|S_{z};+\rangle$ نرمالیزه است مقدار اسپین را بر حسب اندازه خود می نویسیم :
$$S_{z}|S_{z};+\rangle=\frac{\hbar}{2}|S_{z};+\rangle$$
بطور کل :
$$S_{z}|S_{z};\pm\rangle=\pm\frac{\hbar}{2}|S_{z};\pm\rangle$$
$$S_{x}|S_{x};\pm\rangle=\pm\frac{\hbar}{2}|S_{x};\pm\rangle$$
یادآوری میشود که :
$$A|a^{\prime}\rangle=a^{\prime}|a^{\prime}\rangle$$
که در آن A عملگر اندازه گیری، $a^{\prime}$ مقدار ویژه ی عملگر A و $|a^{\prime}\rangle$ حالت ویژه یا کت ویژه ی عملگر A می باشد.
بنابر این $\pm\frac{\hbar}{2}$ ویژه مقادیر و کت ها که بعنوان کت های پایه هستند، ویژه کت هستند. یعنی پایه ها در اینجا همان ویژه کت ها هستند.
هر کت همانند بردارها در فضای اقلیدسی که به صورت مجموع ضرائبی از بردارهای پایه ی i,j,k نوشته میشوند، میتواند به صورت مجموعی از ضرائب پایه خود نوشته شود:
$$|\alpha\rangle=\sum_{a^{\prime}}^{}c_{a^{\prime}}|a^{\prime}\rangle$$
که در آن c ضریبی مختلط، $a^{\prime}$ اندیس ویژه حالت(همانند $a^{"}$ ، $a^{'}$ و ...) و $|a^{\prime}\rangle$ ویژه حالت مربوط به $a^{\prime}$ می باشد.
ضرب داخلی دو ویژه بردار برابر با صفر می باشد که به صورت کلی تری با دلتای کرونکر نوشته میشود:
$$\langle a^{'}|a^{"}\rangle=\delta_{a^{'}a^{"}}$$
اگر طرفین $|\alpha\rangle=\sum_{a^{\prime}}^{}c_{a^{\prime}}|a^{\prime}\rangle$ را در بِرای $\langle a^{"}|$ ضرب کنیم و با توجه به رابطه دلتای کرونکر که در نقاط $a^{"}$ و $a^{'}$ برابر میشوند به دست می آوریم :
$$c_{a^{'}}=\langle a^{'} |\alpha \rangle$$
بنابر این داریم :
$$|\alpha\rangle=\sum_{a^{\prime}}^{}|a^{\prime}\rangle\langle a^{'} |\alpha \rangle$$
دو سمت عبارت، $|\alpha \rangle$ وجود دارد بنابر این نتیجه میگیریم :
$$\sum_{a^{\prime}}^{}|a^{\prime}\rangle\langle a^{'}| =1$$
که 1 ماتریس همانی می باشد. اگر 1 را دو سمت عملگر A قرار دهیم داریم :
$$A=1A1=\sum_{a^{"}}^{}\sum_{a^{'}}^{}|a^{"}\rangle\langle a^{"}|A|a^{'}\rangle\langle a^{'}|$$
در آزمایش اسپین و اندازه گیری ها در مکانیک کوانتومی، چون عملگر اندازه گیری برای به دست آوردن مقادیر حقیقی باید هرمیتی باشد و ویژه کت ها کت های پایه هستند بنابر این $\langle a^{'}|A|a^{"}\rangle$ در رابطه بالا قطری می باشد:
$$\langle a^{"}|A|a^{'}\rangle=\langle a^{'}|A|a^{'}\rangle \delta_{a^{'}a^{"}}=a^{'}\delta_{a^{'}a^{"}}$$
ضرب داخلی ویژه کت ها برابر با 1 بوده و ضرب ماتریس در ویژه حالت برابر با مقدار ویژه در ویژه حالت می باشد که در نهایت برابر با $a^{'}\delta_{a^{'}a^{"}}$ میشود. بنابر این :
$$A=\sum_{a^{'}}{}a^{'}|a^{'}\rangle \langle a^{'}|$$
طبق این رابطه سعی میکنیم عملگر Sz را به دست آوریم :
$$S_{z}=\frac{\hbar}{2}\left [ (|S_{z};+\rangle \langle S_{z};+|)-(|S_{z};-\rangle \langle S_{z};-|)\right]$$
همچنین رابطه زیر نیز ماتریس همانی خواهد بود.
$$1=|S_{z};+\rangle \langle S_{z};+|+|S_{z};-\rangle \langle S_{z};-|$$
صحت سنجی روابط برگرفته شده از آزمایش اپتیکی
با فرض مختلط گرفتن هردو اسپین های Y و X به صورت عمومی سعی میکنیم اختلاف 90 درجه ای مبتنی بر حدس پیشین را به دست آوریم.
در اینجا عموما هردو مختلط گرفته شده اما اگر X را کاملا حقیقی بگیریم ناچارا Y مختلط خواهد بود یا بلعکس.
همچنین به طور قراردادی عبارت اول را حقیقی و عبارت دوم را مختلط در نظر میگیریم.
شکل عمومی حالت:
$$|S_{x};\pm\rangle =\frac{1}{\sqrt{2}}|S_{z};+\rangle\pm\frac{1}{\sqrt{2}}e^{i\sigma_{1}}|S_{z};-\rangle$$
$$|S_{y};\pm\rangle =\frac{1}{\sqrt{2}}|S_{z};+\rangle\pm\frac{1}{\sqrt{2}}e^{i\sigma_{2}}|S_{z};-\rangle$$
عملگر $S_{z}$ را در بخش قبل با توجه به رابطه $A=\sum_{a^{'}}{}a^{'}|a^{'}\rangle \langle a^{'}|$ محاسبه کردیم. اکنون با استفاده از همین رابطه و شکل عمومی حالت در نظر گرفته شده عملگر های $S_{x}$ و $S_{y}$ را نیز حساب میکنیم :
$$S_{x}=\frac{\hbar}{2}\left[(|S_{x};+\rangle \langle S_{x};+|)-(|S_{x};-\rangle \langle S_{x};-|) \right]$$
$$=\frac{\hbar}{2}\left[e^{-i\sigma_{1}}(|S_{z};+\rangle \langle S_{z};-|)+e^{i\sigma_{1}}(|S_{z};-\rangle \langle S_{z};+|) \right]$$
به طریق مشابه برای $S_{y}$
$$S_{y}=\frac{\hbar}{2}\left[e^{-i\sigma_{2}}(|S_{z};+\rangle \langle S_{z};-|)+e^{i\sigma_{2}}(|S_{z};-\rangle \langle S_{z};+|) \right]$$
به طور کلی هنگامی که حالت $|\alpha\rangle$ وارد یک عملگر اندازه گیری میشود احتمال اندازه گیری خروجی به صورت ویژه مقدار $a^{'}$ یا قرارگیری حالت خروجی در ویژه کت $|a^{'}\rangle$ به صورت زیر محاسبه میشود:
$$P_{a^{'}}=|\langle a^{'}|\alpha\rangle|^{2}$$
اگر اسپین Xu وارد دستگاه اندازه گیری اسپین z شود چه مقدار احتمال اندازه گیری $+\frac{\hbar}{2}$ یا $-\frac{\hbar}{2}$ وجود دارد؟ میدانیم احتمال رخداد برای هریک برابر با $\frac{1}{2}$ می باشد. بنابر این حاصل اندازه براکت زیر باید برابر با $\frac{1}{\sqrt{2}}$ باشد.
$$|\langle S_{z};+|S_{x};+\rangle|=|\langle S_{z};-|S_{x};+\rangle|=\frac{1}{\sqrt{2}}$$
برای حالت های ورودی xu و xd در دستگاه اندازه گیری اسپین y برای احتمال اندازه گیری $+\frac{\hbar}{2}$ یا $-\frac{\hbar}{2}$ داریم :
$$|\langle S_{y};\pm|S_{x};+\rangle|=|\langle S_{y};\pm|S_{x};-\rangle|=\frac{1}{\sqrt{2}}$$
حال، شکل عمومی حالت را در روابط بالا قرار میدهیم:
$$\frac{1}{2}|1\pm e^{i(\delta_{1}-\delta_{2})}|=\frac{1}{\sqrt{2}}$$
$$\delta_{1}-\delta_{2}=\pm \frac{\pi}{2}$$
بنابر این نتیجه میگیریم ضرائب $|S_{x};\pm\rangle$و $|S_{y};\pm\rangle$ همگی نمی توانند حقیقی باشند. اگر $|S_{x};\pm\rangle$ حقیقی باشد به ناچار $|S_{y};\pm\rangle$ باید مختلط باشد یا بلعکس. به طور قرارداد $|S_{x};\pm\rangle$ حقیقی در نظر گرفته میشود. همچنین اگر $S_{x}$ حقیقی باشد $S_{y}$ موهومی خالص خواهد بود. این مثال ساده نشان داد بکارگیری اعداد مختلط در مکانیک کوانتومی جزو خصوصیت های بنیادین در مکانیک کوانتومی می باشد. بدین شکل در ابتدا با یک آزمایش اپتیکی تنها یک مثال برای موجودیت انواع دیگر عملگر به کار بردیم و مشاهده نمودیم که امکان حضور ضریب مختلط بنا به علت اختلاف فاز وجود دارد، در ادامه به شکل کلی تر و با فرض مختلط بودن ضرائب و به کار گیری اصول موضوعه مکانیک کوانتومی عملگرهای $S_{y}$ ، $S_{x}$ و $S_{z}$ و کت های x و y و z را مستقل از آزمایش اپتیکی به دست آوردیم.
به طور خلاصه و با قرار دادن $\delta_{1}=0$ و $\delta_{2}=\frac{\pi}{2}$ :
$$S_{z}=\frac{\hbar}{2}\left[(|S_{z};+\rangle \langle S_{z};+|)-(|S_{z};-\rangle \langle S_{z};-|)\right]=\frac{\hbar}{2}\begin{pmatrix}1&0\\0&-1\\\end{pmatrix}$$
$$S_{x}=\frac{\hbar}{2}\left[(|S_{z};+\rangle \langle S_{z};-|)+(|S_{z};-\rangle \langle S_{z};+|)\right]=\frac{\hbar}{2}\begin{pmatrix}0&1\\1&0\\\end{pmatrix}$$
$$S_{y}=\frac{\hbar}{2}\left[(-i|S_{z};+\rangle \langle S_{z};-|)+i(|S_{z};-\rangle \langle S_{z};+|)\right]=\frac{\hbar}{2}\begin{pmatrix}0&-i\\i&0\\\end{pmatrix}$$
$$|S_{x};\pm\rangle=\frac{\sqrt{2}}{2}|S_{z};+\rangle\pm\frac{\sqrt{2}}{2}|S_{z};-\rangle$$
$$|S_{y};\pm\rangle=\frac{\sqrt{2}}{2}|S_{z};+\rangle\pm i\frac{\sqrt{2}}{2}|S_{z};-\rangle$$
$$S_{z}|S_{z};\pm\rangle=\pm\frac{\hbar}{2}|S_{z};+\rangle$$
که در آن ماتریس های زیر به ماتریس های پائولی معروف هستند:
$$\sigma_{1}=\begin{pmatrix}0&1\\1&0\\\end{pmatrix} ,
\sigma_{2}=\begin{pmatrix}0&-i\\i&0\\\end{pmatrix} ,
\sigma_{3}=\begin{pmatrix}1&0\\0&-1\\\end{pmatrix}$$
منابع:
http://alienryderflex.com/
www.wikipedia.org
Modern Quantum Mechanics (J. J. Sakurai)
gstatic.com
lehman.edu/faculty/anchordoqui/400_10.pdf
