اصل و ذره برنولی
اصل برنولی جریان یک سیال را برای جریان ثابت و تراکم ناپذیر در طول یک خط جریان توصیف می کند. اما برای ذره ای از سیال در امتداد یک خط جریان گفته می شود. سوال من این است که ذره مایع به یک مولکول یا گروهی از مولکول ها اشاره دارداصل برنولی چیزی جز $F=ma$ برای حجم های کوچک سیال نیست. به عبارت دیگر، تنها چیزی که می تواند مقداری سیال را شتاب دهد، اختلاف فشار است و بالعکس.
یک مولکول سیال (از آنجایی که دما دارد) بسیار سریع حرکت می کند، اما خیلی دور نمی شود زیرا با مولکول های دیگر برخورد می کند. به آن برخوردهای دائمی «فشار» می گویند.
اگر مولکولهای جلوتر در فشار کمتری باشند به این معنی است که برخورد کمتری در هر ثانیه مشاهده میکنند، بنابراین مولکول اصلی تمایل به جهش در آن جهت دارد. بنابراین فشار کمتر باعث حرکت مایع می شود.
معادلات برنولی زمانی که سیالات مختلف و دبی حجمی درگیر هستندمن در مورد استفاده از معادله برنولی هنگامی که دبی های حجمی چندگانه درگیر هستند، تردید دارم.
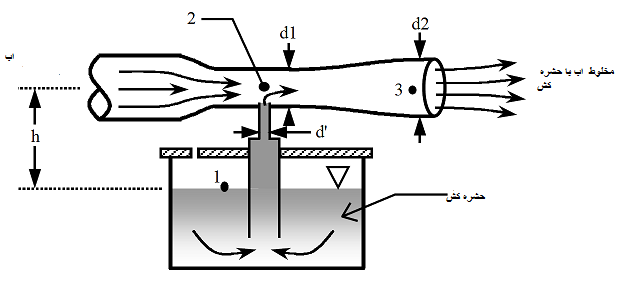
برای مثال دستگاه موجود در تصویر را در نظر بگیرید. آب در لوله اصلی جریان دارد، در حالی که در مخزن زیر حشره کش وجود دارد که به لوله اصلی مکیده می شود. توضیحات تصویر را در اینجا وارد کنید سرعت جریان حجمی آب $Q_{W}$ است، دبی حجمی مورد نظر حشره کش$Q_I$ است. بنابراین در نقطه 3 نرخ جریان $Q_W+Q_I$ خواهد بود.
در کتاب درسی سرعت در نقطه 2 و 3 به عنوان تعیین شده است
$v_{2,\mathrm{water}}=\frac{Q_W}{\pi (\frac{d_1}{2})^2}$
$v_{2,\mathrm{insecticide}}=\frac{Q_I}{\pi (\frac{d'}{2})^2}$
$v_{3,\mathrm{mixture}}=\frac{Q_W+Q_I}{\pi (\frac{d_2}{2})^2}$
و من با آن مشکلی ندارم. مشکلات مربوط به استفاده از معادله برنولی در این زمینه است (که در کتاب درسی یافتم).
ابتدا B.E. بین نقطه 1 تا 2 برای حشره کش استفاده می شود و من با آن مشکلی ندارم.
اما معادله بین نقطه 2 و 3 نیز برای آب و سپس مخلوط استفاده می شود، یعنی
$p_2+\frac{1}{2} \rho_{\mathrm{water}} v^2_{2,\mathrm{water}}=p_3 +\frac{1}{2} \rho_{\mathrm{water}} v^2_{3,\mathrm{mixture}}$
نکته این است که در 3 فقط آب وجود ندارد بلکه مخلوطی وجود دارد، بنابراین سیال متفاوت است: آیا به هر حال می توان از معادله برنولی بین دو نقطه استفاده کرد؟
حدس من منفی است زیرا میتوانم از معادله برنولی بین 2 و 3 استفاده کنم، اما به جای آب، حشرهکش را در نظر بگیرم.
$p_2+\frac{1}{2} \rho_{\mathrm{insecticide}} v^2_{2,\mathrm{insecticide}}=p_3 +\frac{1}{2} \rho_{\mathrm{insecticide}} v^2_{3,\mathrm{mixture}}$
و $v_{2,\mathrm{water}}\neq v_{2,\mathrm{insecticide}}$, حشره کش پس این در تضاد با معادله قبلی است (حداقل مقادیر مختلف ρ مشکل را حل می کند که من شک دارم).
همچنین برای استفاده از برنولی در 3 حدس میزنم که استفاده از یک مقدار خاص از ρ صحیح نیست، زیرا دوباره سیال مخلوطی است.
بنابراین سوال من این است: آیا دلیلی وجود دارد که استفاده از معادله برنولی بین 2 و 3 در این مورد صحیح باشد؟ و چگونه باید از آن استفاده کرد؟در اصل شما نمی توانید برنولی را برای آنچه در واقع یک شبکه (ساده) از لوله ها است اعمال کنید، اما در برخی موارد تقریب ها انجام می شوند.لوله برنولی بیایید معادله برنولی را در قسمت های چپ و میانی لوله اعمال کنیم:
$P_1+\frac12 \rho v_1^2=P_2+\frac12 \rho v_2^2$
از آنجایی که مایعات تراکم ناپذیر هستند (A سطح مقطع لوله است):$A_1v_1=A_2v_2$
بنابراین با یک جایگزین ساده:
$P_2=P_1-\frac12 \rho \Bigg(\Big(\frac{A_1}{A_2}\Big)^2-1\Bigg)v_1^2$
از آنجایی که به عنوان $A_1 > A_2 \implies P_2 < P_1$
حالا برنولی را روی جریان حشره کش بمالید. در نقطه 1 سرعت جریان را ناچیز و فشار را اتمسفر فرض می کنیم (P0):
$P_0=P_2+\frac12 \rho v_i^2+\rho gh$$\implies \frac12 \rho v_i^2=P_0-P_2-\rho gh$
با معادله بالا:
$\frac12 \rho v_i^2=P_0-P_1+\frac12 \rho \Bigg(\Big(\frac{A_1}{A_2}\Big)^2-1\Bigg)v_1^2-\rho gh$
برای اینکه اصلاً جریان حشره کش رو به بالا داشته باشیم، یعنی $v_i > 0$، پس:
$\frac12 \rho \Bigg(\Big(\frac{A_1}{A_2}\Big)^2-1\Bigg)v_1^2 > P_1-P_0+\rho gh$
اگر این شرط رعایت نشود، بخش میانی لوله در واقع آب را به داخل حشرهکش نشت میکند!
اگر برآورده شود و با فرض $v_i\ll v_1$، رویکرد شما باید تقریباً کار کند. اما برای vi بزرگتر باید از روش Cross برای شبکه های لوله استفاده کنید.
من در مورد استفاده از معادله برنولی هنگامی که دبی های حجمی چندگانه درگیر هستند، تردید دارم.
بنابراین شک و تردید شما موجه است، اما برای حجم های کوچک توزیع شده حشره کش، رویکرد تقریبی شما باید کارساز باشد.زیرمجموعه های $w,i,m$ به ترتیب با آب، حشره کش و مخلوط مطابقت دارند.)
ابتدا $Q_m=Q_w+Q_i$فقط اگر $\rho_w=\rho_i=\rho_m$. در غیر این صورت باید نرخ جریان جرمی $\dot{M}_m=\dot{M}_w+\dot{M}_i$ را برای یافتن $v_m$ با فرض اینکه چگالی مخلوط در سطح مقطع در نقطه 3 یکنواخت است معادل سازی کنید.
دوم، شکل معادله برنولی که یادداشت کردهاید، فقط در صورتی که چگالی در طول آن خط جریان ثابت بماند، قابل استفاده است. بنابراین شما باید یک خط ساده پیدا کنید که تغییر چگالی در آن در مقایسه با برخی از چگالی مرجع ناچیز است، مثلاً چگالی متوسط روی آن خط جریان. من نمی دانم کدام یک از معادلات برنولی که نوشته اید معتبر استhope I helped you understand the question. Roham Hesami, sixth
semester of aerospace engineering


رهام حسامی ترم ششم مهندسی هوافضا



