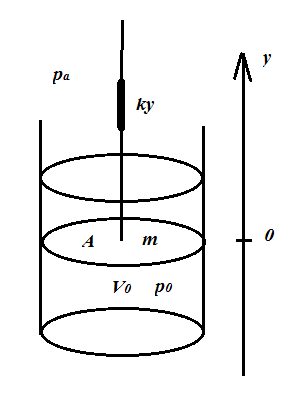
کار انجام شده توسط پیستون در مقابل کار انجام شده توسط اطراف
فرض کنید یک مجموعه پیستون بدون جرم و اصطکاک در ابتدا فشار بیشتری نسبت به فشار خارجی (اتمسفر) دارد و به گونه ای پین شده است که پیستون حرکت نکند. پس از برداشتن پین، پیستون منبسط می شود تا زمانی که فشار داخل پیستون به فشار اتمسفر تبدیل شود. در طی فرآیند، کار انجام شده توسط گاز داخل پیستون است
$W_{\text{piston}}=\int_{V_1}^{V_2} P_{\text{gas}}\cdot \mathrm{d}V$
و کار انجام شده توسط اطراف این است،
$W_{\text{ext}}=\int_{V_1}^{V_2}P_{\text{ext}}\cdot \mathrm{d}V = P_{\text{ext}} \left(V_2 - V_1 \right)
$ما می توانیم فشار خارجی را از انتگرال بیرون بکشیم زیرا به عنوان یک فشار اتمسفر ثابت است.
سوال من این است که کار انجام شده توسط پیستون با کاری که توسط اطراف انجام می شود یکسان نیست زیرا dV یکسان است ، اما ${P}_{\text{gas}}$ در طول فرآیند از $P_ext$ بزرگتر است ، بنابراین کار انجام شده توسط پیستون بزرگتر از کاری است که توسط پیستون انجام می شود. اطراف. آیا آنها نباید یکسان باشند؟تنها مشکل این است که شما در نظر می گیرید که فشار اتمسفر ثابت می ماند. در واقع افزایش می یابد. بگذار توضیح بدهم:
هنگامی که پیستون شما منبسط می شود، حجم اتمسفر را به طور کلی از $V_{0\mathrm{atm}}$ به کاهش می دهد
$V_{1\mathrm{atm}}=V_{0\mathrm{atm}}- \Delta V
\,.$این کاهش حجم منجر به افزایش فشار اتمسفر از$p_{0\text{ext}}$ به بالا می شود
$p_{1\text{ext}}= \frac{p_{0\mathrm{atm}}}{1- \frac{\Delta V}{V_{0\text{atm}}}}
$.حتی اگر تصور کنیم که افزایش فشار بسیار اندک است وقتی ΔV≪V0atm را در نظر بگیریم (همانطور که همیشه هست) تا جایی که بتوان $p_{0\text{ext}}$ را ثابت در نظر گرفت، انرژی از دست رفته به عنوان انرژی پتانسیل در سراسر سیاره پراکنده می شود، درست به همان اندازه که انرژی ذخیره می کنید. در یک بطری تحت فشار
در این مدل من فکر می کنم که جو در بالای آن بسته بود. با این حال، حتی اگر سناریوی سقف باز را در نظر بگیرید، به جای افزایش فشار اتمسفر، انبساط سیستم شما تا حد معینی به بالای جو میافزاید. به هر حال، افزایش ارتفاع اتمسفر منجر به افزایش انرژی پتانسیل گرانشی آن می شود و در نتیجه تعادل کار و انرژی برقرار می شود.
یه سوال خیلی جالب به نظر می رسد متناقض است. بخرید، در مشکل شما شرایطی برای اصطکاک و جرم پیستون داده شده است، اما هیچ محدودیتی برای انتقال حرارت به داخل و خارج یا تغییر دما وجود ندارد. پس این یک مشکل ناقص است. به لطف این نقص، به نظرم می رسد که می تواند یک راه فرار منطقی وجود داشته باشد. به راحتی، هیچ اشاره ای به "متفاوت بودن" فشار داخل و خارج سرنگ حتی پس از برداشتن پین وجود ندارد.
اگر اکنون فرض کنیم که گاز داخل سرنگ یک گاز ایده آل است، آنگاه سیر $P_{gas}$ به عنوان تابعی از V، $P_{gas}(V)V=nRT$ را برآورده می کند، بنابراین،$P_{gas}(V) = nRT/V$
، اما اصلاً فرضی مبنی بر عدم تغییر دما وجود ندارد.
بنابراین اگر حدی را فرض کنیم که در آن سیلندر اصلاً انرژی نمی گیرد، یعنی آنقدر کند که انرژی جنبشی به دست نمی آورد، $P_{gas}(V)$ چه خواهد بود؟ برای اینکه اینطور باشد، باید همیشه $P_{gas} dV = P_{ext} dV$باشد، بنابراین
$P_{gas}=P_{ext}$همیشه راضی خواهد بود تنها راه برای مجبور کردن آن به انجام این کار این است که دما را به راحتی تغییر دهید. اگر ما حتی مقدار کمی از انرژی را به انرژی جنبشی سرنگ به دلیل "گزاره برداشته شده" زیر حمل کنیم.
یعنی دمای گاز در سرنگ می تواند و باید به صورت تابعی از V به شکل زیر اعمال شود.
$P_{gas}(V)=P_{ext} = nRT_{gas}(V)/V$بنابراین،$T_{gas}(V)=P_{ext} V/nR$
این بدان معناست که اگر دمای سرنگ را بتوان به این ترتیب تغییر داد، میتوان یک موقعیت فیزیکی ممکن را به طور مصنوعی ایجاد کرد.
فرض کنید S سطح مقطع پیستون باشد.
هنگامی که گاز داخل سرنگ منبسط می شود (یعنی $P_{gas}>P_{ext}$)، پیستون نیرویی معادل $F_1=P_{gas}S$ از گاز داخل سرنگ در جهت انبساط گاز دریافت می کند.
از طرف دیگر، در این حالت، سرنگ نیرویی معادل $F_2=-P_{ext}S$ از گاز خارج از سرنگ در جهت انبساط گاز دریافت می کند.
بنابراین، نیروی ترکیبی دریافت شده توسط سرنگ $F_{sir} = F_1 + F_2 = (P_{gas} - P_{ext})S$ در جهت انبساط گاز است.
بنابراین، هنگام حرکت در یک مسافت کوچک dl، سرنگ انرژی زیر را دریافت می کند.
$F_{sir}\ dl = (P_{gas} - P_{ext})S\ dl = (P_{gas} - P_{ext})\ dV$
بنابراین، در طول فرآیند شما، انرژی که سرنگ از گازها به دست می آورد، خواهد بود.
${W}_{sir}=\int_{V_1}^{V_2} (P_{gas} - P_{ext}) dV$
اگر هیچ اصطکاک یا نیرویی برای ترمز پیستون وجود نداشته باشد، به نظر می رسد که تفاوت بین$W_{ext}$ و ${W}_{piston}$ (یعنی ${W}_{sir}$ جایی جز انرژی جنبشی سیلندر ندارد.
در چنین شرایطی. اگر جرم استوانه بی نهایت صفر باشد، آیا سرعت سیلندر بی نهایت زیاد نخواهد بود؟ به نظر من این یک موقعیت فیزیکی غیرممکن خواهد بود.
کار انجام شده متفاوت است زیرا پیستون با سرعت بیشتری شتاب می گیرد. در صورت انبساط فشار ثابت (هر دو فشار داخلی و خارجی در همه موارد یکسان است) پیستون به آرامی حرکت می کند. زیرا نیرو برای حرکت پیستون کافی است. اما در مورد شما نیروی داخل به اندازه کافی بالاتر خواهد بود، بنابراین پیستون سریعتر حرکت می کند (یعنی شتاب گرفته). من هم همین شک را داشتم و هنوز در مورد آن شک دارم.I hope I have helped you in understanding the question. Roham Hesami rad, seventh semester
aerospace engineering