منحنی صفحه ای را در نظر بگیرید که با معادله y = f (x) تعریف شده است. فرض کنید که خط مماس به منحنی در نقطه M(x,y) کشیده شده است. مماس یک زاویه α با محور افقی تشکیل می دهد
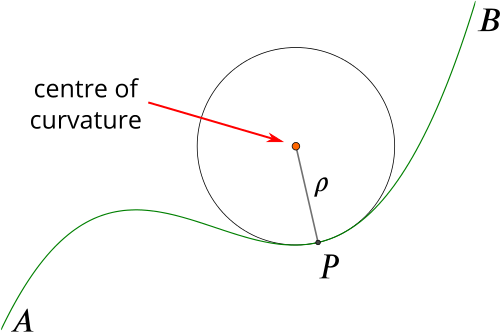 ]با جابجایی Δs در طول کمان منحنی، نقطه M به سمت نقطه M1 حرکت خواهد کرد. در این صورت، موقعیت خط مماس نیز تغییر میکند؛ زاویه شیب خط مماس بر نقطه M1 و محور مثبت x، α+Δα خواهد بود. بنابراین، با حرکت نقطه به اندازه Δs، خط مماس به اندازه Δα میچرخد (فرض شده که وقتی جهت حرکت زاویه α پادساعتگرد باشد، افزایشی خواهد بود.)قدر مطلق نسبت $\frac{{\Delta \alpha }}{{\Delta s}}$ انحنا یا خمیدگی متوسط کمان MM1 نامیده میشود. با حد$\Delta s \to 0,$، انحنای منحنی در نقطه M به صورت زیر محاسبه میشود:$\large K = \lim \limits _ { \Delta s \to 0 } \left | { \frac { { \Delta \alpha } } { { \Delta s } } } \right | .$برای یک منحنی مسطح با معادله y=f(x)، انحنا در نقطه M(x,y) بر حسب مشتقهای اول و دوم تابع$y = f\left( x \right),$ و با فرمول زیر بیان میشود:$K = \frac{{\left| {y^{\prime\prime}\left( x \right)} \right|}}{{{{\left[ {1 + {{\left( {y'\left( x \right)} \right)}^2}} \right]}^{\frac{3}{2}}}}}.$اگر منحنی به فرم پارامتری و با معادلات x=x(t) و y=y(t) تعریف شده باشد، آنگاه انحنا در نقطه M(x,y) با رابطه زیر تعیین میشود:$K = \frac{{\left| {x'y^{\prime\prime} - y'x^{\prime\prime}} \right|}}{{{{\left[ {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2}} \right]}^{\frac{3}{2}}}}}.$اگر یک منحنی با معادله قطبی داده شود، انحنا با فرمول محاسبه می شود$K = \frac{{\left| {{r^2} + 2{{\left( {r'} \right)}^2} - rr^{\prime\prime}} \right|}}{{{{\left[ {{r^2} + {{\left( {r'} \right)}^2}} \right]}^{\frac{3}{2}}}}}.$شعاع هم نسبست عکس با انحنا داره$\large R = \frac { 1 } { K } .$یعنی $R = \frac{{{{\left[ {1 + {{\left( {y'\left( x \right)} \right)}^2}} \right]}^{\frac{3}{2}}}}}{{\left| {y^{\prime\prime}\left( x \right)} \right|}}.$
]با جابجایی Δs در طول کمان منحنی، نقطه M به سمت نقطه M1 حرکت خواهد کرد. در این صورت، موقعیت خط مماس نیز تغییر میکند؛ زاویه شیب خط مماس بر نقطه M1 و محور مثبت x، α+Δα خواهد بود. بنابراین، با حرکت نقطه به اندازه Δs، خط مماس به اندازه Δα میچرخد (فرض شده که وقتی جهت حرکت زاویه α پادساعتگرد باشد، افزایشی خواهد بود.)قدر مطلق نسبت $\frac{{\Delta \alpha }}{{\Delta s}}$ انحنا یا خمیدگی متوسط کمان MM1 نامیده میشود. با حد$\Delta s \to 0,$، انحنای منحنی در نقطه M به صورت زیر محاسبه میشود:$\large K = \lim \limits _ { \Delta s \to 0 } \left | { \frac { { \Delta \alpha } } { { \Delta s } } } \right | .$برای یک منحنی مسطح با معادله y=f(x)، انحنا در نقطه M(x,y) بر حسب مشتقهای اول و دوم تابع$y = f\left( x \right),$ و با فرمول زیر بیان میشود:$K = \frac{{\left| {y^{\prime\prime}\left( x \right)} \right|}}{{{{\left[ {1 + {{\left( {y'\left( x \right)} \right)}^2}} \right]}^{\frac{3}{2}}}}}.$اگر منحنی به فرم پارامتری و با معادلات x=x(t) و y=y(t) تعریف شده باشد، آنگاه انحنا در نقطه M(x,y) با رابطه زیر تعیین میشود:$K = \frac{{\left| {x'y^{\prime\prime} - y'x^{\prime\prime}} \right|}}{{{{\left[ {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2}} \right]}^{\frac{3}{2}}}}}.$اگر یک منحنی با معادله قطبی داده شود، انحنا با فرمول محاسبه می شود$K = \frac{{\left| {{r^2} + 2{{\left( {r'} \right)}^2} - rr^{\prime\prime}} \right|}}{{{{\left[ {{r^2} + {{\left( {r'} \right)}^2}} \right]}^{\frac{3}{2}}}}}.$شعاع هم نسبست عکس با انحنا داره$\large R = \frac { 1 } { K } .$یعنی $R = \frac{{{{\left[ {1 + {{\left( {y'\left( x \right)} \right)}^2}} \right]}^{\frac{3}{2}}}}}{{\left| {y^{\prime\prime}\left( x \right)} \right|}}.$بدیهی است که برای یافتن انحنای بیضی در نقاط و (شکل ) کافی است، زیرا به دلیل تقارن منحنی، انحنای دو راس مخالف بیضی یکسان خواهد بود.برای محاسبه انحنا، راحت است که از معادله متعارف بیضی به معادله به شکل پارامتریک عبور کنیم:$x = a\cos t,\;\;\;y = b\sin t,$پس من میام فرمول اجرا میکنم $x' = {x'_t} = \left( {a\cos t} \right)^\prime = - a\sin t,\;\;\;x^{\prime\prime} = x^{\prime\prime}_{tt} = \left( { - a\sin t} \right)^\prime = - a\cos t;$.و به طور سیمیلار برای y خوب بعد محاسبه من $K = \frac{{\left| {ab\,{{\sin }^2}t + ab\,{{\cos }^2}t} \right|}}{{{{\left( {{a^2}{{\sin }^2}t + {b^2}{{\cos }^2}t} \right)}^{\frac{3}{2}}}}} = \frac{{\left| {ab\left( {{{\sin }^2}t + {{\cos }^2}t} \right)} \right|}}{{{{\left( {{a^2}{{\sin }^2}t + {b^2}{{\cos }^2}t} \right)}^{\frac{3}{2}}}}} = \frac{{ab}}{{{{\left( {{a^2}{{\sin }^2}t + {b^2}{{\cos }^2}t} \right)}^{\frac{3}{2}}}}}.$و من دو مقدار برای t انتخاب میکنم$K\left( A \right) = K\left( {t = 0} \right) = \frac{{ab}}{{{{\left( {{a^2}{{\sin }^2}0 + {b^2}{{\cos }^2}0} \right)}^{\frac{3}{2}}}}} = \frac{{ab}}{{{{\left( {{b^2}} \right)}^{\frac{3}{2}}}}} = \frac{{ab}}{{{b^3}}} = \frac{a}{{{b^2}}};$و $K\left( B \right) = K\left( {t = \frac{\pi }{2}} \right) = \frac{{ab}}{{{{\left( {{a^2}{{\sin }^2}\frac{\pi }{2} + {b^2}{{\cos }^2}\frac{\pi }{2}} \right)}^{\frac{3}{2}}}}} = \frac{{ab}}{{{{\left( {{a^2}} \right)}^{\frac{3}{2}}}}} = \frac{{ab}}{{{a^3}}} = \frac{b}{{{a^2}}}.$انحنای ابربیضی را که با معادلات پارامتری تعریف شده است، بیابید$x\left( t \right) = a\, {\cos ^n}t,\; y\left( t \right) = b\,{\sin ^n}t,$ابربیضی ها منحنی های خوبی هستند که شکل آن ها بین دایره و مربع است. آنها کاربردهای زیادی در طراحی و مهندسی دارند.
شکل یک منحنی با انحنای آن مشخص می شود. در این مسئله، فرمول کلی انحنای یک ابربیضی با توان مثبت دلخواه را استخراج می کنیم.$K \text = \frac{{ab{2^{1 - n}}\left| {\left( {2 - n} \right){{\sin }^{n - 1}}2t} \right|}}{{{{n\left[ {{a^2}{{\cos }^{2n - 2}}t\,{{\sin }^2}t + {b^2}{{\sin }^{2n - 2}}t\,{{\cos }^2}t} \right]}^{\frac{3}{2}}}}}.$
خمیدگی در حقیقت معادل با میزان تغییر جهت یک تابع برداری یا همان تابع پارامتری نسبت به پارامتر وابسته است. روابط زیادی به منظور بدست آوردن خمیدگی توابع پارامتری وجود دارد. با این حال تعریف کلی خمیدگی به صورت زیر است.$\Large \kappa = \left | { \frac { { d \, \overrightarrow T } } { {d s } } } \right|$در رابطه فوق، s برابر با طول خم و T نشان دهنده بردار مماس به خم است. همانطور که در مطلب توابع برداری نیز بیان شد، به منظور بدست آوردن خمیدگی یک تابع، در ابتدا باید، آن را به صورت پارامتری بیان کرده، سپس قادر خواهیم بود تا خمیدگی آن را محاسبه کنیم.$\large \kappa = \frac{{\left\| {\overrightarrow T ^ {\prime} \left( t \right)} \right\|}}{{\left\| {\overrightarrow r ^ {\prime} \left( t \right)} \right\|}}\hspace{1.0in}\kappa = \frac{{\left\| {\overrightarrow r ^{ \prime } \left( t \right) \times \overrightarrow r ^{\prime\prime} \left( t \right)} \right\|}}{{{{\left\| {\overrightarrow r ^ {\prime} \left( t \right)} \right\|}^3}}}$اجازه دهید یک منحنی صفحه به صورت پارامتریک توسط بردار شعاع تعریف شود در حالی که یک نقطه در امتداد منحنی حرکت می کند، جهت مماس تغییر می کندانحنای منحنی را می توان به عنوان نسبت زاویه چرخش مماس به طول قوس پیموده شده این نسبت تعریف کرد.
انحنای متوسط منحنی نامیده می شود. هنگامی که نقطه به نقطه نزدیک می شود، انحنای منحنی را در نقطه به دست می آوریم$k = \lim\limits_{\Delta s \to 0} \frac{{\Delta \varphi }}{{\Delta s}} = \frac{{d\varphi }}{{ds}}.$واضح است که انحنا در حالت کلی بسته به جهت چرخش مماس می تواند مثبت یا منفی باشد.
اگر یک منحنی با بردار شعاع تعریف شود، انحنای آن توسط بردار مشخص می شود$k = \frac{{\mathbf{r'} \times \mathbf{r^{\prime\prime}}}}{{{{\left| {\mathbf{r'}} \right|}^3}}},$
اگر مختصات یک منحنی به صورت پارامتری به صورت و مشخص شود، فرمول محاسبه انحنا به شکل$k = \frac{{x'y^{\prime\prime} - y'x^{\prime\prime}}}{{{{\left[ {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2}} \right]}^{\frac{3}{2}}}}}.$در موردی که یک منحنی در مختصات قطبی به شکل داده می شود انحنای آن با عبارت تعریف می شود$k\left( \varphi \right) = \frac{{{\rho ^2} + 2{{\left( {\rho'} \right)}^2} - \rho \rho^{\prime\prime}}}{{{{\left[ {{\rho ^2} + {{\left( {\rho'} \right)}^2}} \right]}^{\frac{3}{2}}}}}.$hope I helped you understand the question. Roham Hesami, sixth
semester of aerospace engineering



