dusty نوشته شده:قبل از این کار شما باید یک فرض فیزیکی انجام بدید.
فرض خودِ فضا یا فضا-زمان.
یعنی یک اسم[فضا] به علاوه یک واحد اندازهگیری[متر].
سلام و درود بر شما
الف) همونطور که در تعریف بنده دیدید،
فرض کردم که یک فضای برداری
)
روی میدان
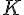
داریم.
ب) نکته ی قابل توجه این هست که در اینجا این میدان نقشی کلیدی رو بازی می کنه،
چرا که استقلال خطی و همچنین مولد بودن پایه های
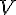
شدیداً به میدان
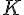
بستگی داره.
ج) خود این فضای برداری تعریف دقیق داره؛
در واقع در این فضا،
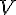
یک مجموعه است به علاوه ی دو تابع جمع (
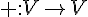
) و ضرب اسکالر (
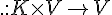
).
به طور کلی فضا ها متشکل از یک مجموعه هستند، به علاوه ی دست کم یک تابع،
که این مجموعه لزوماً روی تابع بسته است.
مثلاً فضای برداری روی تابع جمع، که خصوصاً در اینجا یک گروه آبلی رو تشکیل می ده، پس نتیجتاً باید بسته باشه.
چ) برای تعریف فضای برداری نیازی به تعریف فاصله نداریم.
در صورت لزوم می شه یک تابع برای فضا های برداری تعریف کرد (تابع فاصله)،
که فضای برداری ما رو به فضای متریک ارتقاء می ده،
اما در اینجا اصلاً نیازی به فضای متریک نداریم.
ح) فقط یادمون باشه که تعریف بالا برای فضا های متناهی بُعد بود.
فضاهای با بعد نامتناهی مثل فضای هیلبرت (که توی کوانتوم هم می خونیمش) از اساس فرق دارن.
فرمودید:
dusty نوشته شده:ما میتونیم نظریه هامون رو در یک فضای n بُعدی(ریاضی) بنویسیم (که n میتونه یک عدد غیر صحیح باشه) طوری که تمام نتایج فیزیکی نظریه های قبلی رو محترم بدونه.
ولی این بُعد(فضای ریاضیاتی) چه تاثیری در فیزیک تجربی داره؟ هیچی!
اون چیزی که در قابل اندازه گیری هستش همان کمیت های اولیهس.
پس از نظر فیزیکی بُعد همان کمیت های تعریف شدس
خ) بله ...
قبول دارم که این یک بحث ریاضی بود که ما کردیم،
ولی در فیزیک پیشرفته، دقیقاً از همین ها باید استفاده کنیم.
مثلاً در فیزیک پیشرفته، دیگه نمی شه از مفهوم مختصات به جای بعد استفاده کرد و الا بحثمون روی هوا است!
باید دقیق حرف زد و نمی شه که همینطوری یک چیزی رو دیمی و دلبخواهی بگیم!
این طوری نمی شه، چرا که در این صورت هرکس هر شهودی که داره رو می خواد به عنوان تعریف اعلام کنه.
فیزیک با ادبیات و فلسفه فرق می کنه، و با وجود این که یک علم تجربی هست، ریاضی مشرب هست.
د) شاخه ی بسیار زیبا و اصیلی هست در ریاضیات کاربردی به نام
ریاضی فیزیک یا
Mathematical physics
که متاسفانه توی ایران بهش توجه درخوری نشده، این بحث ها در واقع در حوزه ی متمتیکال فیزیکس جای دارند.

