هوافضا
- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: هوافضا
چگونه یک دیفیوزر (در اثر زمین) هوای مقابل خود را تسریع می کند؟یک دیفیوزر سرعت را کاهش می دهد و فشار را افزایش می دهد، بنابراین اگر یک وضعیت شیب فشار نامطلوب داشته باشیم چگونه یک دیفیوزر به هوای جلوی خود شتاب می دهد؟
آیا بهتر نیست که فشار کمتری (به جای فشار بیشتر) را در انتهای آن قرار دهیم که هوا را جلوی آن "کشش"/شتاب می دهد؟به بیان ساده، هدف اصلی دیفیوزر این است که انتقال از هوای سریع در زیر بدنه خودرو را با بازگشت به سرعت هوای محیط پشت خودرو، تدریجی کند.
یک منطقه فشار بالا در جلوی ماشین از برخورد ذرات هوا با وسیله نقلیه وجود دارد، و یک منطقه کم فشار در پشت ماشین وجود دارد، زیرا جریان هوا در حال تلاش برای پیوستن مجدد به طرف دیگر است. این جریان زیاد تا کم هوا را به زیر خودرو که در آن فضا محدود است می کشد. این فضای محدود منجر به افزایش سرعت و کاهش فشار می شود، بنابراین نیروی رو به پایین افزایش می یابد زیرا فشار زیر خودرو کمتر از فشار روی بالا و کناره های خودرو است. این معادله برنولی در کار است.
با این حال، هوای که به سرعت در حال حرکت است، گرادیان فشار نامطلوبی را در عقب خودرو تجربه می کند و جداسازی جریان هوا منجر به تلاطم قابل توجهی می شود. این تلاطم نه تنها کشش را افزایش می دهد، بلکه سرعت تخلیه هوا از زیر خودرو را محدود می کند. با شکل دادن دقیق یک دیفیوزر، جریان هوا را می توان به تدریج کاهش داد، بازگشت آن به جریان محیط را آسان کرد، تلاطم را به حداقل رساند که باعث افزایش سرعت جریان در زیر خودرو، کاهش فشار و افزایش بیشتر نیروی رو به پایین بر روی چرخ ها می شود.
دیفیوزر به گونه ای طراحی شده است که سرعت جریان هوا را در جلوی این قیف افزایش دهد تا یک ناحیه کم فشار در جلوی قیف را فشار دهد و به طور مؤثرتری هوا را به داخل دیفیوزر بکشد.
آیا بهتر نیست که فشار کمتری (به جای فشار بیشتر) را در انتهای آن قرار دهیم که هوا را جلوی آن "کشش"/شتاب می دهد؟به بیان ساده، هدف اصلی دیفیوزر این است که انتقال از هوای سریع در زیر بدنه خودرو را با بازگشت به سرعت هوای محیط پشت خودرو، تدریجی کند.
یک منطقه فشار بالا در جلوی ماشین از برخورد ذرات هوا با وسیله نقلیه وجود دارد، و یک منطقه کم فشار در پشت ماشین وجود دارد، زیرا جریان هوا در حال تلاش برای پیوستن مجدد به طرف دیگر است. این جریان زیاد تا کم هوا را به زیر خودرو که در آن فضا محدود است می کشد. این فضای محدود منجر به افزایش سرعت و کاهش فشار می شود، بنابراین نیروی رو به پایین افزایش می یابد زیرا فشار زیر خودرو کمتر از فشار روی بالا و کناره های خودرو است. این معادله برنولی در کار است.
با این حال، هوای که به سرعت در حال حرکت است، گرادیان فشار نامطلوبی را در عقب خودرو تجربه می کند و جداسازی جریان هوا منجر به تلاطم قابل توجهی می شود. این تلاطم نه تنها کشش را افزایش می دهد، بلکه سرعت تخلیه هوا از زیر خودرو را محدود می کند. با شکل دادن دقیق یک دیفیوزر، جریان هوا را می توان به تدریج کاهش داد، بازگشت آن به جریان محیط را آسان کرد، تلاطم را به حداقل رساند که باعث افزایش سرعت جریان در زیر خودرو، کاهش فشار و افزایش بیشتر نیروی رو به پایین بر روی چرخ ها می شود.
دیفیوزر به گونه ای طراحی شده است که سرعت جریان هوا را در جلوی این قیف افزایش دهد تا یک ناحیه کم فشار در جلوی قیف را فشار دهد و به طور مؤثرتری هوا را به داخل دیفیوزر بکشد.

- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: هوافضا
چرا جریان در دیفیوزر وجود دارد؟من تعجب می کنم که چرا در یک دیفیوزر جریان وجود دارد: بنابراین به گفته برنولی هنگامی که جریان سرعت می گیرد، فشار دینامیکی کاهش می یابد و فشار استاتیک افزایش می یابد.
فرض کنید هیچ تلفاتی (در فشار کل) وجود ندارد: بنابراین در یک دیفیوزور فشار استاتیک در ناحیه وسیعتر از ناحیه باریک بیشتر است. پس ذرات سیال با فشار استاتیکی بالاتر مبارزه می کنند و از انرژی جنبشی خود برای غلبه بر آن استفاده می کنند؟
من یاد گرفتم که برای داشتن یک جریان نیاز به گرادیان فشار دارید و ذرات از فشار بالاتر به ناحیه فشار پایین تر حرکت می کنند.. اما اینجا نیست؟بله، ذرات سیال در حال مبارزه با فشار استاتیکی بالاتر هستند و از انرژی جنبشی خود برای غلبه بر آن استفاده می کنند. مثل یک آونگ است.همانطور که شما می گویید، هیچ افتی در فشار کل وجود ندارد، بنابراین فشار دینامیکی باید به فشار استاتیک تبدیل شود. با در نظر گرفتن این موضوع، فشار استاتیک هرگز نمی تواند آنقدر بالا رود که به طور کامل بر فشار دینامیکی برای توقف جریان غلبه کند. تا زمانی که یک سیال تحت فشار استاتیک جایی برای رفتن داشته باشد، به آنجا می رود، یعنی تبدیل به فشار دینامیکی می شود.
برای یک مولکول، هیچ تفاوتی بین فشار دینامیک و استاتیک وجود ندارد. این فقط می تواند (گاز) یا فشار (مایع) را در یک جهت در یک زمان حرکت کند، که اساس اصل معادل برنولی است. این مفهوم فشار در سیالات را تفسیری می کند. آنچه را که در یک سیال می گذرد، توصیف یا تعریف نمی کند. این مدلی است که کار با آنچه در یک سیال می گذرد را ممکن می کند.
با این حال، برای داشتن یک جریان، به یک گرادیان فشار نیاز دارید، و ذرات از فشار بالاتر به ناحیه فشار پایینتر حرکت میکنند، که در این مورد عمدتاً در خارج از دیفیوزر شما یافت میشود.
فرض کنید هیچ تلفاتی (در فشار کل) وجود ندارد: بنابراین در یک دیفیوزور فشار استاتیک در ناحیه وسیعتر از ناحیه باریک بیشتر است. پس ذرات سیال با فشار استاتیکی بالاتر مبارزه می کنند و از انرژی جنبشی خود برای غلبه بر آن استفاده می کنند؟
من یاد گرفتم که برای داشتن یک جریان نیاز به گرادیان فشار دارید و ذرات از فشار بالاتر به ناحیه فشار پایین تر حرکت می کنند.. اما اینجا نیست؟بله، ذرات سیال در حال مبارزه با فشار استاتیکی بالاتر هستند و از انرژی جنبشی خود برای غلبه بر آن استفاده می کنند. مثل یک آونگ است.همانطور که شما می گویید، هیچ افتی در فشار کل وجود ندارد، بنابراین فشار دینامیکی باید به فشار استاتیک تبدیل شود. با در نظر گرفتن این موضوع، فشار استاتیک هرگز نمی تواند آنقدر بالا رود که به طور کامل بر فشار دینامیکی برای توقف جریان غلبه کند. تا زمانی که یک سیال تحت فشار استاتیک جایی برای رفتن داشته باشد، به آنجا می رود، یعنی تبدیل به فشار دینامیکی می شود.
برای یک مولکول، هیچ تفاوتی بین فشار دینامیک و استاتیک وجود ندارد. این فقط می تواند (گاز) یا فشار (مایع) را در یک جهت در یک زمان حرکت کند، که اساس اصل معادل برنولی است. این مفهوم فشار در سیالات را تفسیری می کند. آنچه را که در یک سیال می گذرد، توصیف یا تعریف نمی کند. این مدلی است که کار با آنچه در یک سیال می گذرد را ممکن می کند.
با این حال، برای داشتن یک جریان، به یک گرادیان فشار نیاز دارید، و ذرات از فشار بالاتر به ناحیه فشار پایینتر حرکت میکنند، که در این مورد عمدتاً در خارج از دیفیوزر شما یافت میشود.

- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: هوافضا
چرا بخش دیفیوزر نیروی رانش در موتور جت ایجاد می کند؟در شروع چرخه، هوا به موتور القا می شود و فشرده می شود. شتابهای عقب در طی مراحل کمپرسور و افزایش فشار ناشی از آن، نیروی واکنشی زیادی را در جهت جلو ایجاد میکند. در مرحله بعدی سفر، هوا از دیفیوزر عبور می کند، جایی که نیروی واکنشی کوچکی اعمال می کند، همچنین در جهت رو به جلو.
من قسمت اول پاراگراف را میدانم که کمپرسور نیروی رانش به جلو را فراهم میکند، زیرا هوا را به عقب فشار میدهد. اما چرا دیفیوزر نیروی رانش به جلو را نیز فراهم می کند؟ و همچنین چرا نازل نیروی رانش به عقب را فراهم می کند؟
با توجه به درک من از مکانیک سیالات اساسی، آیا یک نازل نباید مانند آبپاش در باغ یا شلنگ آتش نشانی، نیروی رانش به جلو را فراهم کند؟ و آیا یک دیفیوزر نباید نیروی رانش به عقب را فراهم کند، زیرا سرعت خروجی کمتر از سرعت ورودی است و بنابراین m نقطه X (v - u) منفی است؟درک من چه اشکالی دارد؟اما چرا دیفیوزر نیروی رانش به جلو را نیز فراهم می کند؟
دیفیوزر جریان را کاهش می دهد تا ترکیب سوخت و هوا و احتراق کمی دیرتر آسان شود. اگر فقط روی سرعت های ورود و خروج تمرکز کنید، هیچ نیروی رانشی وجود نخواهد داشت.
با این حال، اگر به فشار روی دیواره های پخش کننده نگاه کنید، نتیجه متفاوتی ظاهر می شود. جریان آهسته تر به معنای فشار استاتیک بالاتر است و فشار کل درست در خروجی کمپرسور در حال حاضر بالاترین میزان در کل موتور است. فشار روی دیوارهای پخش کننده در حال گشاد شدن، موتور را در واقع به دلیل شیب رو به جلو بردار فشار (که عمود بر دیواره های دیفیوزور عمل می کند) به جلو می راند. صفحه جت پالس پیوند شده شما این را به خوبی توضیح می دهد.
البته اگر جریان گرم نمی شد و در نتیجه در پایین دست شتاب بیشتری می گرفت، هیچ نیروی رانشی حاصل نمی شد. بنابراین دیفیوزر به تنهایی نیروی رانش ایجاد نمی کند. این تنها زمانی اتفاق می افتد که در داخل یک موتور جت در حال کار قرار گیرد.
و همچنین چرا نازل نیروی رانش به عقب را فراهم می کند؟
همیشه اینطور نیست، اما در اینجا نازل شکل همگرا دارد که به تسریع جریان مادون صوت کمک می کند و فشار باقیمانده را به سرعت تبدیل می کند. اکنون دیوارها دارای شیب رو به عقب هستند، بنابراین بردار فشار روی آنها یک جزء رو به عقب را ایجاد می کند. علاوه بر این، سرعت جریان بالا در امتداد دیواره های نازل بزرگ باعث ایجاد اصطکاک می شود که باید در نظر گرفته شود.
برای مقایسه، به مخروط پشت چرخ های توربین نگاه کنید. سهم رانش آن فقط از فشار رو به جلو که بر روی آن وارد می شود ناشی می شود.و آیا یک دیفیوزر نباید نیروی رانش به عقب را فراهم کند، زیرا سرعت خروجی کمتر از سرعت ورودی است و بنابراین$\dot{m}\times(v - u)$ منفی است؟
قوانین حفاظت در فیزیک ابزار بسیار خوبی هستند. آنها به شما این امکان را می دهند که بدون نگاه کردن به جزئیات جزئی فرآیند واقعی، مقدار زیادی محاسبه کنید. و این یک مثال عالی است: شما می توانید نیروی رانش کل موتور را از تغییر تکانه سیال کار محاسبه کنید. اما این به شما نمی گوید که نیرو در واقع چگونه اعمال می شود، فقط مجموع نیروهای وارد بر کل موتور است.
تفکیک رانش جزییات جزئی فرآیند است. و در آن سطح، تنها راه ایجاد نیرو، فشار سیال است و از آنجایی که فشار همیشه عمود بر سطح عمل می کند، تنها سطوح رو به عقب می توانند بر روی آنها رانش به جلو اعمال کنند، در حالی که هر سطح رو به جلو، رانش منفی بر آنها اثر می گذارد.
و در اسپرینکلر هم فرقی نمی کند. فشار داخل بر روی تمام دیوارها تأثیر می گذارد، اما مقداری در نازل جایی که آب به بیرون می ریزد وجود ندارد، بنابراین نیروی وارد بر دیوار مقابل غالب است.
تفاوت بین دیفیوزر و داکت در توربین ها چیست؟
من این مقاله را خوانده ام که به مزایای دیفیوزرها در توربین های جریان متقاطع می پردازد.
(تاکید از من است):
بهبود خارقالعاده یک CP زمانی حاصل شد که انحراف تا 22.5 درجه برای هیدروفویل شکل و تا 30 درجه برای دیفیوزر متقارن افزایش یافت. رفتار مشابهی در جریانهای انحرافی در مورد یک روتور منفرد مجرای نیز رخ داده است که نشان می دهد که این یک ویژگی CFT است.
من در مورد تفاوت بین داکت و دیفیوزر از نظر توربین گیج شدم.
یک توربین بادی اصلاح شده با یک پخش کننده باد مخروطی شکل که برای افزایش راندمان تبدیل نیروی باد به برق استفاده می شود. افزایش راندمان به دلیل افزایش سرعت باد که دیفیوزر می تواند ارائه دهد امکان پذیر است.
سوال من این است که تفاوت این دو چیست؟ آیا عملکردهای متفاوتی دارند؟
من می پرسم زیرا به نظر می رسد نویسنده به طور ضمنی اشاره می کند که این دو با هم متفاوت هستند.
تعریف دیفیوزر عبارت است از:
دیفیوزر (واگرا) مجرای شکلی است که سیالی که در آن جریان دارد کندتر می شود و فشار از ورودی به خروجی افزایش می یابد
.جزء رانش فشار دقیقاً چیست و چرا وجود دارد؟یشتر نوشته ها، اصطلاح «تراست فشاری» را - در مقابل « رانش حرکتی» - با توضیح اینکه در شرایط رانش زیاد در یک اگزوز خفه شده، گاز خروجی به سرعت صوت میرسد و نمیتوان آن را بیشتر شتاب داد و در نتیجه فشار استاتیک را افزایش داد. گاز فراتر از فشار اتمسفر افزایش می یابد، این رانش فشار به رانش تکانه اضافه می شود تا کل رانش را تشکیل دهد.
اولاً - به خوبی شناخته شده است که سرعت گازهای خروجی هواپیما به راحتی می تواند مافوق صوت شود، مثلاً با یک جت جنگنده ... چرا این محدودیت در موتورهای توربوفن است؟
ثانیاً - اغلب در مطالب آموزشی تأکید می شود که باید از فکر کردن به نیروی رانش به عنوان عمل / فشار دادن به هوای محیط پشت موتور، بر خلاف تفکر قانون 3 نیوتن اجتناب کنید... اما آیا این دقیقاً همان فشار نیست. رانش است؟ با فشار × ناحیه ای که روی آن عمل می کند تعریف می شود...در واقع، گازهای خروجی را می توان فراتر از 1 ماخ منبسط کرد و انجام این کار منجر به رانش بیشتر ناشی از راندمان بیشتر پیشرانه می شود. مشکل این است که گاز تحت فشار با انبساط سطح مقطع زمانی که کمتر از M1 است، و در زمانی که بالاتر از M1 است، منبسط می شود.
بنابراین برای دستیابی به انبساط کامل تا فشار محیط p0 در سرعت اگزوز مافوق صوت، ما به مقطعی نیاز داریم که برای همه شرایط پرواز باریک و سپس منبسط شود. شکل زیر نحوه انجام این کار در جت های جنگنده مافوق صوت را نشان می دهد: با اگزوز جت اجکتور.
از توربین های گاز هواپیما نوشته سی جی هاتمن، تی یو دلفت
اگزوز اولیه در داخل یک لوله نصب می شود و گاز خروجی در حال انبساط جریان ثانویه را می مکد که انبساط جریان اولیه را کم می کند تا به تدریج انجام شود. جریان ثانویه را می توان به عنوان بخش واگرای اگزوز در نظر گرفت و از اگزوز فلزی واقعی از گرمای پس سوز محافظت می کند. در جت های جنگنده مافوق صوت، هر دو اگزوز اولیه و ثانویه قابل تنظیم هستند: عکس سمت چپ برای سرعت مافوق صوت، سمت راست برای سرعت مافوق صوت.
بنابراین انبساط کامل امکان پذیر است و در عین حال پیچیده است، با نیاز به تغییر مداوم نازل های اگزوز.
اولاً - به خوبی شناخته شده است که سرعت گازهای خروجی هواپیما به راحتی می تواند مافوق صوت شود، مثلاً با یک جت جنگنده ... چرا این محدودیت در موتورهای توربوفن است؟
از آنجایی که جریان اصلی توربوفن از طریق فن است که فقط یک کمپرسور است، در این جریان احتراق صورت نمی گیرد. در بیشتر شرایط، جریان بای پس در سرعتهای زیر صوت به طور کامل گسترش مییابد - اگر اینطور نباشد، ساخت چهار نازل اگزوز تنظیمشده متحدالمرکز مانند تصویر بالا پیچیده و سنگین خواهد بود، برای بهره بسیار محدود. تنها بالاتر از M1.5، افزایش نیروی رانش قابل توجهی از انبساط کامل مافوق صوت وجود خواهد داشت.
ثانیاً - اغلب در مطالب آموزشی تأکید می شود که باید از فکر کردن به نیروی رانش به عنوان عمل / فشار دادن به هوای محیط پشت موتور، بر خلاف تفکر قانون 3 نیوتن اجتناب کنید... اما آیا این دقیقاً همان فشار نیست. رانش است؟ با فشار × ناحیه ای که روی آن عمل می کند تعریف می شود...نازل خفه شده
پرواز مافوق صوت یا مافوق صوت، ورودی، کمپرسور و دیفیوزر موتور جت، همگی سرعت هوا را کاهش می دهند تا سرعت مافوق صوت را کاهش دهند تا احتراق انجام شود. هنگامی که دما به شدت افزایش می یابد، بخشی از این انرژی به سرعت تبدیل می شود.
به دلیل دمای احتراق بالا، سرعت صوت بسیار بالاتر است، بنابراین جریان جرمی در مسیر خود به سمت نازل مادون صوت است. باحال درسته؟ در جریان مادون صوت، با فشرده شدن هوا، سرعت آن افزایش می یابد و فشار آن کاهش می یابد.
افت فشار طراحی شده در نازل منجر به عبور جریان جرمی مشخص به دلیل اختلاف فشار می شود.
آن را بیشتر رها کنید و در باریک ترین قسمت نازل، گلو، سرعت به 1 ماخ می رسد. اکنون جریان خفه شده است.
آن را بیشتر رها کنید، و دیگر شتاب مادون صوت از طریق فشردن آن گلوی ثابت از نظر فیزیکی امکان پذیر نیست. سرعت جریان جرمی به حداکثر خود رسیده است (حتی برای موشک).
نازلهای توربوفن در جتلاینرها (همحلقهای) حتی به دلایل کارایی به طور هدفمند این کار را انجام نمیدهند - هر چه سرعت اگزوز به جریان آزاد نزدیکتر باشد، پیشرانه کارآمدتر است. همچنین، نگاه کنید به: ویکی پدیا: راندمان پیشرانه § موتورهای جت
جنگنده ها و جت های با کارایی بالا
مبارزان دو ترفند دارند:
اگزوز داغتر و حتی اگزوز داغتر با استفاده از پس سوز. هرچه هوا گرمتر باشد، سرعت صوت بیشتر است و به اگزوز اجازه می دهد که 1 ماخ سریعتر از جریان آزاد 1 ماخ باشد. دوباره باحاله درسته؟
دمای خروجی سرعت خروج صوت را تعیین می کند که سرعت خروج را تعیین می کند.
نازل های هندسی متغیر: یک گلوگاه در حال انبساط اجازه می دهد تا جریان جرم بیشتری در گلوی خفه شده جریان یابد. در اعداد ماخ پرواز بالاتر، ورودی فشرده سازی بیشتری را فراهم می کند و بنابراین سرعت جریان جرم بیشتری ممکن می شود. به همین دلیل است که وقتی هواپیما سریعتر است و/یا از نیروی رانش بالاتر استفاده میکند، گلوها باز میشوند.
رانش فشار
به دلیل شرایط کاری متفاوت در نازلهای ثابت در موشکها، "راست فشاری" برای معادله رانش، همراه با تغییر در تکانه مورد نیاز است - این یکی یا دیگری نیست، فقط این است که رانش فشار برای موتورهای توربین ناچیز است:
نازل یک موتور توربین معمولاً طوری طراحی می شود که فشار خروجی را برابر جریان آزاد قرار دهد. در آن صورت، عبارت ناحیه فشار در معادله کلی برابر با صفر است.
من قسمت اول پاراگراف را میدانم که کمپرسور نیروی رانش به جلو را فراهم میکند، زیرا هوا را به عقب فشار میدهد. اما چرا دیفیوزر نیروی رانش به جلو را نیز فراهم می کند؟ و همچنین چرا نازل نیروی رانش به عقب را فراهم می کند؟
با توجه به درک من از مکانیک سیالات اساسی، آیا یک نازل نباید مانند آبپاش در باغ یا شلنگ آتش نشانی، نیروی رانش به جلو را فراهم کند؟ و آیا یک دیفیوزر نباید نیروی رانش به عقب را فراهم کند، زیرا سرعت خروجی کمتر از سرعت ورودی است و بنابراین m نقطه X (v - u) منفی است؟درک من چه اشکالی دارد؟اما چرا دیفیوزر نیروی رانش به جلو را نیز فراهم می کند؟
دیفیوزر جریان را کاهش می دهد تا ترکیب سوخت و هوا و احتراق کمی دیرتر آسان شود. اگر فقط روی سرعت های ورود و خروج تمرکز کنید، هیچ نیروی رانشی وجود نخواهد داشت.
با این حال، اگر به فشار روی دیواره های پخش کننده نگاه کنید، نتیجه متفاوتی ظاهر می شود. جریان آهسته تر به معنای فشار استاتیک بالاتر است و فشار کل درست در خروجی کمپرسور در حال حاضر بالاترین میزان در کل موتور است. فشار روی دیوارهای پخش کننده در حال گشاد شدن، موتور را در واقع به دلیل شیب رو به جلو بردار فشار (که عمود بر دیواره های دیفیوزور عمل می کند) به جلو می راند. صفحه جت پالس پیوند شده شما این را به خوبی توضیح می دهد.
البته اگر جریان گرم نمی شد و در نتیجه در پایین دست شتاب بیشتری می گرفت، هیچ نیروی رانشی حاصل نمی شد. بنابراین دیفیوزر به تنهایی نیروی رانش ایجاد نمی کند. این تنها زمانی اتفاق می افتد که در داخل یک موتور جت در حال کار قرار گیرد.
و همچنین چرا نازل نیروی رانش به عقب را فراهم می کند؟
همیشه اینطور نیست، اما در اینجا نازل شکل همگرا دارد که به تسریع جریان مادون صوت کمک می کند و فشار باقیمانده را به سرعت تبدیل می کند. اکنون دیوارها دارای شیب رو به عقب هستند، بنابراین بردار فشار روی آنها یک جزء رو به عقب را ایجاد می کند. علاوه بر این، سرعت جریان بالا در امتداد دیواره های نازل بزرگ باعث ایجاد اصطکاک می شود که باید در نظر گرفته شود.
برای مقایسه، به مخروط پشت چرخ های توربین نگاه کنید. سهم رانش آن فقط از فشار رو به جلو که بر روی آن وارد می شود ناشی می شود.و آیا یک دیفیوزر نباید نیروی رانش به عقب را فراهم کند، زیرا سرعت خروجی کمتر از سرعت ورودی است و بنابراین$\dot{m}\times(v - u)$ منفی است؟
قوانین حفاظت در فیزیک ابزار بسیار خوبی هستند. آنها به شما این امکان را می دهند که بدون نگاه کردن به جزئیات جزئی فرآیند واقعی، مقدار زیادی محاسبه کنید. و این یک مثال عالی است: شما می توانید نیروی رانش کل موتور را از تغییر تکانه سیال کار محاسبه کنید. اما این به شما نمی گوید که نیرو در واقع چگونه اعمال می شود، فقط مجموع نیروهای وارد بر کل موتور است.
تفکیک رانش جزییات جزئی فرآیند است. و در آن سطح، تنها راه ایجاد نیرو، فشار سیال است و از آنجایی که فشار همیشه عمود بر سطح عمل می کند، تنها سطوح رو به عقب می توانند بر روی آنها رانش به جلو اعمال کنند، در حالی که هر سطح رو به جلو، رانش منفی بر آنها اثر می گذارد.
و در اسپرینکلر هم فرقی نمی کند. فشار داخل بر روی تمام دیوارها تأثیر می گذارد، اما مقداری در نازل جایی که آب به بیرون می ریزد وجود ندارد، بنابراین نیروی وارد بر دیوار مقابل غالب است.
تفاوت بین دیفیوزر و داکت در توربین ها چیست؟
من این مقاله را خوانده ام که به مزایای دیفیوزرها در توربین های جریان متقاطع می پردازد.
(تاکید از من است):
بهبود خارقالعاده یک CP زمانی حاصل شد که انحراف تا 22.5 درجه برای هیدروفویل شکل و تا 30 درجه برای دیفیوزر متقارن افزایش یافت. رفتار مشابهی در جریانهای انحرافی در مورد یک روتور منفرد مجرای نیز رخ داده است که نشان می دهد که این یک ویژگی CFT است.
من در مورد تفاوت بین داکت و دیفیوزر از نظر توربین گیج شدم.
یک توربین بادی اصلاح شده با یک پخش کننده باد مخروطی شکل که برای افزایش راندمان تبدیل نیروی باد به برق استفاده می شود. افزایش راندمان به دلیل افزایش سرعت باد که دیفیوزر می تواند ارائه دهد امکان پذیر است.
سوال من این است که تفاوت این دو چیست؟ آیا عملکردهای متفاوتی دارند؟
من می پرسم زیرا به نظر می رسد نویسنده به طور ضمنی اشاره می کند که این دو با هم متفاوت هستند.
تعریف دیفیوزر عبارت است از:
دیفیوزر (واگرا) مجرای شکلی است که سیالی که در آن جریان دارد کندتر می شود و فشار از ورودی به خروجی افزایش می یابد
.جزء رانش فشار دقیقاً چیست و چرا وجود دارد؟یشتر نوشته ها، اصطلاح «تراست فشاری» را - در مقابل « رانش حرکتی» - با توضیح اینکه در شرایط رانش زیاد در یک اگزوز خفه شده، گاز خروجی به سرعت صوت میرسد و نمیتوان آن را بیشتر شتاب داد و در نتیجه فشار استاتیک را افزایش داد. گاز فراتر از فشار اتمسفر افزایش می یابد، این رانش فشار به رانش تکانه اضافه می شود تا کل رانش را تشکیل دهد.
اولاً - به خوبی شناخته شده است که سرعت گازهای خروجی هواپیما به راحتی می تواند مافوق صوت شود، مثلاً با یک جت جنگنده ... چرا این محدودیت در موتورهای توربوفن است؟
ثانیاً - اغلب در مطالب آموزشی تأکید می شود که باید از فکر کردن به نیروی رانش به عنوان عمل / فشار دادن به هوای محیط پشت موتور، بر خلاف تفکر قانون 3 نیوتن اجتناب کنید... اما آیا این دقیقاً همان فشار نیست. رانش است؟ با فشار × ناحیه ای که روی آن عمل می کند تعریف می شود...در واقع، گازهای خروجی را می توان فراتر از 1 ماخ منبسط کرد و انجام این کار منجر به رانش بیشتر ناشی از راندمان بیشتر پیشرانه می شود. مشکل این است که گاز تحت فشار با انبساط سطح مقطع زمانی که کمتر از M1 است، و در زمانی که بالاتر از M1 است، منبسط می شود.
بنابراین برای دستیابی به انبساط کامل تا فشار محیط p0 در سرعت اگزوز مافوق صوت، ما به مقطعی نیاز داریم که برای همه شرایط پرواز باریک و سپس منبسط شود. شکل زیر نحوه انجام این کار در جت های جنگنده مافوق صوت را نشان می دهد: با اگزوز جت اجکتور.
از توربین های گاز هواپیما نوشته سی جی هاتمن، تی یو دلفت
اگزوز اولیه در داخل یک لوله نصب می شود و گاز خروجی در حال انبساط جریان ثانویه را می مکد که انبساط جریان اولیه را کم می کند تا به تدریج انجام شود. جریان ثانویه را می توان به عنوان بخش واگرای اگزوز در نظر گرفت و از اگزوز فلزی واقعی از گرمای پس سوز محافظت می کند. در جت های جنگنده مافوق صوت، هر دو اگزوز اولیه و ثانویه قابل تنظیم هستند: عکس سمت چپ برای سرعت مافوق صوت، سمت راست برای سرعت مافوق صوت.
بنابراین انبساط کامل امکان پذیر است و در عین حال پیچیده است، با نیاز به تغییر مداوم نازل های اگزوز.
اولاً - به خوبی شناخته شده است که سرعت گازهای خروجی هواپیما به راحتی می تواند مافوق صوت شود، مثلاً با یک جت جنگنده ... چرا این محدودیت در موتورهای توربوفن است؟
از آنجایی که جریان اصلی توربوفن از طریق فن است که فقط یک کمپرسور است، در این جریان احتراق صورت نمی گیرد. در بیشتر شرایط، جریان بای پس در سرعتهای زیر صوت به طور کامل گسترش مییابد - اگر اینطور نباشد، ساخت چهار نازل اگزوز تنظیمشده متحدالمرکز مانند تصویر بالا پیچیده و سنگین خواهد بود، برای بهره بسیار محدود. تنها بالاتر از M1.5، افزایش نیروی رانش قابل توجهی از انبساط کامل مافوق صوت وجود خواهد داشت.
ثانیاً - اغلب در مطالب آموزشی تأکید می شود که باید از فکر کردن به نیروی رانش به عنوان عمل / فشار دادن به هوای محیط پشت موتور، بر خلاف تفکر قانون 3 نیوتن اجتناب کنید... اما آیا این دقیقاً همان فشار نیست. رانش است؟ با فشار × ناحیه ای که روی آن عمل می کند تعریف می شود...نازل خفه شده
پرواز مافوق صوت یا مافوق صوت، ورودی، کمپرسور و دیفیوزر موتور جت، همگی سرعت هوا را کاهش می دهند تا سرعت مافوق صوت را کاهش دهند تا احتراق انجام شود. هنگامی که دما به شدت افزایش می یابد، بخشی از این انرژی به سرعت تبدیل می شود.
به دلیل دمای احتراق بالا، سرعت صوت بسیار بالاتر است، بنابراین جریان جرمی در مسیر خود به سمت نازل مادون صوت است. باحال درسته؟ در جریان مادون صوت، با فشرده شدن هوا، سرعت آن افزایش می یابد و فشار آن کاهش می یابد.
افت فشار طراحی شده در نازل منجر به عبور جریان جرمی مشخص به دلیل اختلاف فشار می شود.
آن را بیشتر رها کنید و در باریک ترین قسمت نازل، گلو، سرعت به 1 ماخ می رسد. اکنون جریان خفه شده است.
آن را بیشتر رها کنید، و دیگر شتاب مادون صوت از طریق فشردن آن گلوی ثابت از نظر فیزیکی امکان پذیر نیست. سرعت جریان جرمی به حداکثر خود رسیده است (حتی برای موشک).
نازلهای توربوفن در جتلاینرها (همحلقهای) حتی به دلایل کارایی به طور هدفمند این کار را انجام نمیدهند - هر چه سرعت اگزوز به جریان آزاد نزدیکتر باشد، پیشرانه کارآمدتر است. همچنین، نگاه کنید به: ویکی پدیا: راندمان پیشرانه § موتورهای جت
جنگنده ها و جت های با کارایی بالا
مبارزان دو ترفند دارند:
اگزوز داغتر و حتی اگزوز داغتر با استفاده از پس سوز. هرچه هوا گرمتر باشد، سرعت صوت بیشتر است و به اگزوز اجازه می دهد که 1 ماخ سریعتر از جریان آزاد 1 ماخ باشد. دوباره باحاله درسته؟
دمای خروجی سرعت خروج صوت را تعیین می کند که سرعت خروج را تعیین می کند.
نازل های هندسی متغیر: یک گلوگاه در حال انبساط اجازه می دهد تا جریان جرم بیشتری در گلوی خفه شده جریان یابد. در اعداد ماخ پرواز بالاتر، ورودی فشرده سازی بیشتری را فراهم می کند و بنابراین سرعت جریان جرم بیشتری ممکن می شود. به همین دلیل است که وقتی هواپیما سریعتر است و/یا از نیروی رانش بالاتر استفاده میکند، گلوها باز میشوند.
رانش فشار
به دلیل شرایط کاری متفاوت در نازلهای ثابت در موشکها، "راست فشاری" برای معادله رانش، همراه با تغییر در تکانه مورد نیاز است - این یکی یا دیگری نیست، فقط این است که رانش فشار برای موتورهای توربین ناچیز است:
نازل یک موتور توربین معمولاً طوری طراحی می شود که فشار خروجی را برابر جریان آزاد قرار دهد. در آن صورت، عبارت ناحیه فشار در معادله کلی برابر با صفر است.

- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: هوافضا
خلبانان اتوماتیک و هواپیمایی
خلبانان اتوماتیک یا خلبانان اتوماتیک وسیله ای برای کنترل فضاپیماها ، هواپیماها ، کشتی های آبی ، موشک ها و وسایل نقلیه بدون دخالت مداوم انسان هستند.
در دنیای هواپیماها ، خلبان اتوماتیک با دقت بیشتری به عنوان سیستم کنترل پرواز خودکار (AFCS) توصیف می شود. AFCS بخشی از یک هواپیما است اویونیک - به الکترونیکی سیستم، تجهیزات و دستگاه های مورد استفاده برای کنترل سیستم های کلیدی از هواپیما و پرواز آن است. علاوه بر سیستم های کنترل پرواز ، اویونیک شامل وسایل الکترونیکی برای ارتباطات ، ناوبری ، جلوگیری از برخورد و آب و هوا است. استفاده اصلی از AFCS تأمین خلبان در مراحل خسته کننده پرواز ، مانند سفرهای دریایی با ارتفاع زیاد بود. خلبانان اتوماتیک پیشرفته می توانند کارهای بسیار بیشتری انجام دهند ، حتی مانورهای بسیار دقیق مانند فرود هواپیما در شرایط دید صفر را انجام دهند.
اگرچه تنوع زیادی در سیستم های خلبان اتوماتیک وجود دارد ، اما بیشتر آنها را می توان با توجه به تعداد قطعات یا سطوح طبقه بندی شده ، طبقه بندی كرد. برای درک این بحث ، کمک می کند تا با سه سطح کنترل اساسی که بر نگرش هواپیما تأثیر می گذارند آشنا شوید. اولین بالابرها ، دستگاههایی هستند که در دم هواپیما کنترل می شوند (نوسان هواپیما در اطراف یک محور افقی عمود بر جهت حرکت). سکان نیز بر روی دم هواپیما واقع شده است. وقتی سکان به سمت تخته سمت راست متمایل می شود (راست) ، هواپیما خمیازه می کشد - در یک محور عمودی می پیچد - در آن جهت. وقتی سکان به پورت (سمت چپ) متمایل می شود ، صنعت در جهت مخالف خمیازه می کشد. سرانجام ، ailerons در لبه عقب هر بال هواپیما را از یک طرف به طرف دیگر بچرخانید.
خلبانان اتوماتیک می توانند همه یا همه این سطح را کنترل کنند. خلبان اتوماتیک تک محور مدیریت فقط یک مجموعه ای از کنترل، معمولا ailerons. این نوع ساده از خلبان اتوماتیک به عنوان "تسطیح بال" شناخته می شود زیرا با کنترل رول ، بال های هواپیما را روی یک پیچ صاف نگه می دارد. یک خلبان اتوماتیک دو محوره آسانسورها و هواپیماها را مدیریت می کند. سرانجام ، یک خلبان اتوماتیک سه محوره هر سه سیستم کنترل اساسی را کنترل می کند: آیلرون ،بالابرو سکان.
کامپیوتری با چندین پردازنده پرسرعت است. برای جمع آوری اطلاعات لازم برای کنترل هواپیما ، پردازنده ها با سنسورهای واقع در سطوح اصلی کنترل ارتباط برقرار می کنند. آنها همچنین می توانند داده ها را از سایر سیستم ها و تجهیزات هواپیما از جمله ژیروسکوپ ، شتاب سنج ، ارتفاع سنج ، قطب نما و شاخص های سرعت هوا جمع آوری کنند .
سپس پردازنده ها در AFCS داده های ورودی را گرفته و با استفاده از محاسبات پیچیده ، آنها را با مجموعه ای از حالت های کنترل مقایسه می کنند. حالت کنترل ، تنظیماتی است که توسط خلبان وارد می شود و جزئیات خاصی از پرواز را تعریف می کند. نمونه ، یک حالت کنترل وجود دارد که نحوه حفظ ارتفاع هواپیما را تعیین می کند. حالت های کنترلی نیز وجود دارد که سرعت هوا ، هدینگ و مسیر پرواز را حفظ می کند.
این محاسبات مشخص می کند که هواپیما از دستورات تنظیم شده در حالت های کنترل اطاعت می کند یا خیر. سپس پردازنده ها سیگنال هایی را به واحدهای مختلف مکانیسم مکانیکی ارسال می کنند. سرو مکانیسم یا به طور خلاصه سروو وسیله ای است که کنترل مکانیکی را از راه دور فراهم می کند. یک سروو برای هر سطح کنترل موجود در سیستم خلبان اتوماتیک وجود دارد. سرووها از دستورالعمل های رایانه استفاده می کنند و از موتور یا هیدرولیک برای جابجایی سطوح کنترل کاردستی استفاده می کنند و مطمئن می شوند هواپیما مسیر و نگرش مناسب خود را حفظ می کند.
. توجه داشته باشید که شماتیک اولیه یک خلبان اتوماتیک مانند یک حلقه به نظر می رسد ، سنسورها داده ها را به کامپیوتر خلبان خودکار می فرستند ، که اطلاعات را پردازش می کند و سیگنال ها را به سروو منتقل می کند ، که سطح کنترل را حرکت می دهد ، که باعث تغییر وضعیت هواپیما می شود ، مجموعه داده های جدید در سنسورها ، که دوباره کل روند را شروع می کند. این نوع حلقه بازخورد در عملکرد سیستم های خلبان اتوماتیک نقشی اساسی دارد.توجه کنید بر اساس کنترل تطبیقی Adaptive Systems عمل میکند
«تطبیق یافتن» معادل “to adapt” و به معنی «تغییر دادن به گونهای که رفتار موجود با شرایط جدید مطابقت داشته باشد» است. کنترل تطبیقی نیز بر همین مطابقت با تغییر اشاره دارد. همانطور که گفتیم، طراحی خلبانهای خودکار برای هواپیماها یکی از انگیزههای اولیه برای تحقیقات در زمینه کنترل تطبیقی بود. هواپیماها در سرعتها و ارتفاعهای مختلفی کار میکنند و دینامیک آنها غیرخطی و متغیر با زمان است. برای یک نقطه کار مشخص (سرعت و ارتفاع)، دینامیک پیچیده هواپیما را میتوان با با یک مدل خطی تقریب زد. برای مثال، در نقطه کار i، مدل خطی هواپیما به فرم زیر است:$ \large \begin {align*}
\dot {x} & = A _ i x + B _ i u, \;\; x ( 0 ) = x _ 0 \\
y & = C _ i ^ \top x + D _ i u
\end {align*} \;\;\;\;\; (1)$
که در آن، AiوBi، Ci و Di تابع شرایط نقطه کار i هستند. وقتی هواپیما در شرایط مختلف پرواز قرار گیرد، نقاط کار تغییر کرده و منجر به مقادیر مختلف $A_i $و$B_i $و$ C_i$و$ D_ i$ خواهد شد. از آنجایی که پاسخ خروجی $ y(t)$ اطلاعاتی درباره حالت x و همچنین پارامترها دارد، انتظار میرود یک کنترلکننده فیدبک پیشرفته این توانایی را داشته باشد که تغییرات پارامتر را با پردازش$y(t) $
یاد گرفته و از بهرههای مناسب برای سازگاری با آنها استفاده کند. این گفته منجر به یک ساختار کنترل فیدبک میشود که کنترل تطبیقی بر آن بنا شده است. ساختار این کنترلکننده از یک حلقه فیدبک و یک کنترلکننده با بهرههای قابل تنظیم تشکیل شده است کنترل مقاوم و کنترل تطبیقی برای غلبه بر تغییرات پارامتر که در محدودههای کراندار قرار دارد، میتوان یک کنترلکننده فیدبک با بهره ثابت طراحی کرد. کنترلکنندهای که در آن، $G (s) $ تابع تبدیل دستگاه و $C( s) $ تابع تبدیل کنترلکننده است.
رایانه خلبان اتوماتیک سیگنالی را به سرویسهای کنترل کننده هواپیماهای هواپیما می فرستد . سیگنال یک دستور بسیار خاص است که به سروو می گوید یک تنظیم دقیق را انجام دهد.
هر سروو دارای یک موتور الکتریکی کوچک است که مجهز به کلاچ لغزنده است و از طریق کابل لبه ، کابل aileron را می گیرد. وقتی کابل حرکت می کند ، سطوح کنترل نیز مطابق آن حرکت می کنند.
همانطور که آیلرون ها بر اساس داده های ورودی تنظیم می شوند ، بال ها به سمت عقب حرکت می کنند.
کامپیوتر خلبان اتوماتیک هنگامی که سنسور موقعیت در بال تشخیص می دهد که بالها دوباره یکنواخت هستند ، فرمان را حذف می کند.
سرووها فشار خود را بر روی کابل های aileron متوقف می کنند.
، به طور مداوم ، چندین بار در ثانیه ، بسیار سریعتر و روانتر از آنچه یک خلبان انسانی می تواند کار کند ، کار می کند. خلبانان اتوماتیک دو و سه محوره با استفاده از چندین پردازنده که چندین سطح را کنترل می کنند ، از اصول یکسانی پیروی می کنند. بعضی از هواپیماها حتی کامپیوترهایی برای کنترل رانش موتور دارند. سیستم های خلبان خودکار و اتو تراست می توانند با هم کار کنند تا مانورهای بسیار پیچیده ای را انجام دهند.
خلبانان خودکار می توانند هواپیما را بسیار روانتر از خلبانان انسانی کنترل کنند.
خلبانان اتوماتیک می توانند خراب شود . یک مشکل معمول نوعی خرابی سروو است ، یا به دلیل موتور بد یا اتصال نامناسب. یک حسگر موقعیت نیز می تواند از کار بیفتد ، در نتیجه اطلاعات ورودی به رایانه خلبان خودکار از بین می رود. خوشبختانه ، خلبانان اتوماتیک برای هواپیماهای سرنشین دار به عنوان یک خطای ایمنی طراحی شده اند - یعنی هیچ نقصی در خلبان اتوماتیک نمی تواند از به کارگیری موثر لغو دستی جلوگیری کند. برای لغو کردن خلبان خودکار ، یکی از اعضای خدمه به سادگی باید سیستم را جدا کند ، یا با چرخاندن یک سوئیچ برق یا اگر این کار نمی کند ، با کشیدن قطع کننده مدار خلبان خودکار .
برخی از سقوط های هواپیما را مسئول شرایطی می دانند که خلبانان نتوانسته اند از سیستم کنترل پرواز خودکار جدا شوند. در پایان خلبانان با تنظیماتی که خلبان خودکار انجام می دهد مبارزه می کنند و نمی توانند بفهمند که چرا هواپیما همان کاری را که از آن خواسته اند انجام نمی دهد. به همین دلیل است که برنامه های آموزش پرواز فقط برای چنین سناریویی تمرین می کنند. خلبانان باید بدانند که چگونه از هر ویژگی AFCS استفاده کنند ، اما همچنین باید نحوه خاموش کردن و پرواز بدون آن را بدانند. آنها همچنین باید از یک برنامه دقیق نگهداری و تعمیرات پیروی کنند تا اطمینان حاصل کنند که همه سنسورها و سرووها از عملکرد خوبی برخوردار هستند. برای هرگونه تنظیم یا اصلاح در سیستم های کلیدی ممکن است نیاز به دستکاری خلبان اتوماتیک باشد. به عنوان مثال ، تغییری که در ابزارهای ژیروسکوپی ایجاد شده نیاز به تنظیم مجدد تنظیمات در خلبان اتوماتیک داردکامپیوتر .
نکته برای دانستن خلبان خودکار ، باید بدانید که هنگام پرواز ، یک هواپیما حدود سه محور را حرکت می دهد که X ، Y و Z یا محور جانبی ، محور طولی و محور عمودی است یا به عنوان Roll axis ، Pitch axis و Yaw شناخته می شود. سه سطح کنترل اساسی وجود دارد که می توان از خلبان توسط خلبان برای انتقال هواپیما به این محورها استفاده کرد. رول با حرکت Aileron کنترل می شود ، Pitch با حرکت آسانسور و Yaw با حرکت Rudder کنترل می شود. Pilot دارای یک میله کنترل یا یک چرخ کنترل برای کنترل هواپیماها و آسانسورها است در حالی که سکان با استفاده از پدال های سکان کنترل می شود. .
با دیدن اصول کنترل هواپیما ، به شما بگویم که در سیستم خلبان اتوماتیک ، این سطوح کنترل نیز می توانند توسط محرک های الکتریکی به صورت مکانیکی به میله های کنترل متصل شوند که ورودی خلبان را به سطح کنترل متصل می کنند. در حالی که در هوا هستید ، اگر یک خلبان هواپیما را به مسیر و ارتفاع دلخواه برساند و کنترل خود را ترک کند ، هواپیما به طور مداوم در همان حالت پرواز نمی کند بلکه به دلیل تلاطم ، رانش نامتقارن و غیره به آرامی از سر یا ارتفاع مورد نظر خود منحرف می شود. او باید به طور مداوم کنترل های خود را انجام دهد و هواپیما را در وضعیت مطلوب خود نگه دارد. اما با خلبان اتوماتیک ، اوضاع متفاوت است. این سیستم دارای سنسورهای مختلفی (به طور کلی ژیروسکوپ) است که برای ایجاد هرگونه اختلال در سه محور تعبیه شده است. آنها این ورودی ها را به صورت سیگنال های الکتریکی به کامپیوتر می دهند. رایانه تصمیم می گیرد كه كدام سطح كنترل شود تا چه اندازه این اختلال اصلاح شود و سیگنال را به محرك الكتریكی مناسب می فرستد همانطور كه قبلاً اشاره كردم. سطح کنترل حرکت می کند و هواپیما به حالت اولیه خود باز می گردد. باز هم سنسورهایی نصب شده اند که این حرکت اصلاحی هواپیما را گرفته و سیگنال های الکتریکی را به کامپیوتر می فرستند (گاهی اوقات محرک خود سیگنال بازخورد را می فرستد). سپس رایانه سیگنال اصلاح اصلی را قطع می کند. بنابراین محرک ها حرکت بیشتر کنترل ها را متوقف می کنند. این نمودار ساده را بررسی کنید.
به غیر از ورودی های سنسورها ، خلبان همچنین می تواند ورودی خود را از طریق واحد کنترل خلبان خودکار به کامپیوتر خلبان خودکار وارد کند. در این حالت خلبان خودکار هواپیما را مطابق ورودی های خلبان حرکت می دهد. در هر زمان خاص یا در مواقع اضطراری ، خلبان همیشه گزینه ای برای قطع خلبان اتوماتیک و گرفتن کنترل دارد.
خلبانان اتوماتیک یا خلبانان اتوماتیک وسیله ای برای کنترل فضاپیماها ، هواپیماها ، کشتی های آبی ، موشک ها و وسایل نقلیه بدون دخالت مداوم انسان هستند.
در دنیای هواپیماها ، خلبان اتوماتیک با دقت بیشتری به عنوان سیستم کنترل پرواز خودکار (AFCS) توصیف می شود. AFCS بخشی از یک هواپیما است اویونیک - به الکترونیکی سیستم، تجهیزات و دستگاه های مورد استفاده برای کنترل سیستم های کلیدی از هواپیما و پرواز آن است. علاوه بر سیستم های کنترل پرواز ، اویونیک شامل وسایل الکترونیکی برای ارتباطات ، ناوبری ، جلوگیری از برخورد و آب و هوا است. استفاده اصلی از AFCS تأمین خلبان در مراحل خسته کننده پرواز ، مانند سفرهای دریایی با ارتفاع زیاد بود. خلبانان اتوماتیک پیشرفته می توانند کارهای بسیار بیشتری انجام دهند ، حتی مانورهای بسیار دقیق مانند فرود هواپیما در شرایط دید صفر را انجام دهند.
اگرچه تنوع زیادی در سیستم های خلبان اتوماتیک وجود دارد ، اما بیشتر آنها را می توان با توجه به تعداد قطعات یا سطوح طبقه بندی شده ، طبقه بندی كرد. برای درک این بحث ، کمک می کند تا با سه سطح کنترل اساسی که بر نگرش هواپیما تأثیر می گذارند آشنا شوید. اولین بالابرها ، دستگاههایی هستند که در دم هواپیما کنترل می شوند (نوسان هواپیما در اطراف یک محور افقی عمود بر جهت حرکت). سکان نیز بر روی دم هواپیما واقع شده است. وقتی سکان به سمت تخته سمت راست متمایل می شود (راست) ، هواپیما خمیازه می کشد - در یک محور عمودی می پیچد - در آن جهت. وقتی سکان به پورت (سمت چپ) متمایل می شود ، صنعت در جهت مخالف خمیازه می کشد. سرانجام ، ailerons در لبه عقب هر بال هواپیما را از یک طرف به طرف دیگر بچرخانید.
خلبانان اتوماتیک می توانند همه یا همه این سطح را کنترل کنند. خلبان اتوماتیک تک محور مدیریت فقط یک مجموعه ای از کنترل، معمولا ailerons. این نوع ساده از خلبان اتوماتیک به عنوان "تسطیح بال" شناخته می شود زیرا با کنترل رول ، بال های هواپیما را روی یک پیچ صاف نگه می دارد. یک خلبان اتوماتیک دو محوره آسانسورها و هواپیماها را مدیریت می کند. سرانجام ، یک خلبان اتوماتیک سه محوره هر سه سیستم کنترل اساسی را کنترل می کند: آیلرون ،بالابرو سکان.
کامپیوتری با چندین پردازنده پرسرعت است. برای جمع آوری اطلاعات لازم برای کنترل هواپیما ، پردازنده ها با سنسورهای واقع در سطوح اصلی کنترل ارتباط برقرار می کنند. آنها همچنین می توانند داده ها را از سایر سیستم ها و تجهیزات هواپیما از جمله ژیروسکوپ ، شتاب سنج ، ارتفاع سنج ، قطب نما و شاخص های سرعت هوا جمع آوری کنند .
سپس پردازنده ها در AFCS داده های ورودی را گرفته و با استفاده از محاسبات پیچیده ، آنها را با مجموعه ای از حالت های کنترل مقایسه می کنند. حالت کنترل ، تنظیماتی است که توسط خلبان وارد می شود و جزئیات خاصی از پرواز را تعریف می کند. نمونه ، یک حالت کنترل وجود دارد که نحوه حفظ ارتفاع هواپیما را تعیین می کند. حالت های کنترلی نیز وجود دارد که سرعت هوا ، هدینگ و مسیر پرواز را حفظ می کند.
این محاسبات مشخص می کند که هواپیما از دستورات تنظیم شده در حالت های کنترل اطاعت می کند یا خیر. سپس پردازنده ها سیگنال هایی را به واحدهای مختلف مکانیسم مکانیکی ارسال می کنند. سرو مکانیسم یا به طور خلاصه سروو وسیله ای است که کنترل مکانیکی را از راه دور فراهم می کند. یک سروو برای هر سطح کنترل موجود در سیستم خلبان اتوماتیک وجود دارد. سرووها از دستورالعمل های رایانه استفاده می کنند و از موتور یا هیدرولیک برای جابجایی سطوح کنترل کاردستی استفاده می کنند و مطمئن می شوند هواپیما مسیر و نگرش مناسب خود را حفظ می کند.
. توجه داشته باشید که شماتیک اولیه یک خلبان اتوماتیک مانند یک حلقه به نظر می رسد ، سنسورها داده ها را به کامپیوتر خلبان خودکار می فرستند ، که اطلاعات را پردازش می کند و سیگنال ها را به سروو منتقل می کند ، که سطح کنترل را حرکت می دهد ، که باعث تغییر وضعیت هواپیما می شود ، مجموعه داده های جدید در سنسورها ، که دوباره کل روند را شروع می کند. این نوع حلقه بازخورد در عملکرد سیستم های خلبان اتوماتیک نقشی اساسی دارد.توجه کنید بر اساس کنترل تطبیقی Adaptive Systems عمل میکند
«تطبیق یافتن» معادل “to adapt” و به معنی «تغییر دادن به گونهای که رفتار موجود با شرایط جدید مطابقت داشته باشد» است. کنترل تطبیقی نیز بر همین مطابقت با تغییر اشاره دارد. همانطور که گفتیم، طراحی خلبانهای خودکار برای هواپیماها یکی از انگیزههای اولیه برای تحقیقات در زمینه کنترل تطبیقی بود. هواپیماها در سرعتها و ارتفاعهای مختلفی کار میکنند و دینامیک آنها غیرخطی و متغیر با زمان است. برای یک نقطه کار مشخص (سرعت و ارتفاع)، دینامیک پیچیده هواپیما را میتوان با با یک مدل خطی تقریب زد. برای مثال، در نقطه کار i، مدل خطی هواپیما به فرم زیر است:$ \large \begin {align*}
\dot {x} & = A _ i x + B _ i u, \;\; x ( 0 ) = x _ 0 \\
y & = C _ i ^ \top x + D _ i u
\end {align*} \;\;\;\;\; (1)$
که در آن، AiوBi، Ci و Di تابع شرایط نقطه کار i هستند. وقتی هواپیما در شرایط مختلف پرواز قرار گیرد، نقاط کار تغییر کرده و منجر به مقادیر مختلف $A_i $و$B_i $و$ C_i$و$ D_ i$ خواهد شد. از آنجایی که پاسخ خروجی $ y(t)$ اطلاعاتی درباره حالت x و همچنین پارامترها دارد، انتظار میرود یک کنترلکننده فیدبک پیشرفته این توانایی را داشته باشد که تغییرات پارامتر را با پردازش$y(t) $
یاد گرفته و از بهرههای مناسب برای سازگاری با آنها استفاده کند. این گفته منجر به یک ساختار کنترل فیدبک میشود که کنترل تطبیقی بر آن بنا شده است. ساختار این کنترلکننده از یک حلقه فیدبک و یک کنترلکننده با بهرههای قابل تنظیم تشکیل شده است کنترل مقاوم و کنترل تطبیقی برای غلبه بر تغییرات پارامتر که در محدودههای کراندار قرار دارد، میتوان یک کنترلکننده فیدبک با بهره ثابت طراحی کرد. کنترلکنندهای که در آن، $G (s) $ تابع تبدیل دستگاه و $C( s) $ تابع تبدیل کنترلکننده است.
رایانه خلبان اتوماتیک سیگنالی را به سرویسهای کنترل کننده هواپیماهای هواپیما می فرستد . سیگنال یک دستور بسیار خاص است که به سروو می گوید یک تنظیم دقیق را انجام دهد.
هر سروو دارای یک موتور الکتریکی کوچک است که مجهز به کلاچ لغزنده است و از طریق کابل لبه ، کابل aileron را می گیرد. وقتی کابل حرکت می کند ، سطوح کنترل نیز مطابق آن حرکت می کنند.
همانطور که آیلرون ها بر اساس داده های ورودی تنظیم می شوند ، بال ها به سمت عقب حرکت می کنند.
کامپیوتر خلبان اتوماتیک هنگامی که سنسور موقعیت در بال تشخیص می دهد که بالها دوباره یکنواخت هستند ، فرمان را حذف می کند.
سرووها فشار خود را بر روی کابل های aileron متوقف می کنند.
، به طور مداوم ، چندین بار در ثانیه ، بسیار سریعتر و روانتر از آنچه یک خلبان انسانی می تواند کار کند ، کار می کند. خلبانان اتوماتیک دو و سه محوره با استفاده از چندین پردازنده که چندین سطح را کنترل می کنند ، از اصول یکسانی پیروی می کنند. بعضی از هواپیماها حتی کامپیوترهایی برای کنترل رانش موتور دارند. سیستم های خلبان خودکار و اتو تراست می توانند با هم کار کنند تا مانورهای بسیار پیچیده ای را انجام دهند.
خلبانان خودکار می توانند هواپیما را بسیار روانتر از خلبانان انسانی کنترل کنند.
خلبانان اتوماتیک می توانند خراب شود . یک مشکل معمول نوعی خرابی سروو است ، یا به دلیل موتور بد یا اتصال نامناسب. یک حسگر موقعیت نیز می تواند از کار بیفتد ، در نتیجه اطلاعات ورودی به رایانه خلبان خودکار از بین می رود. خوشبختانه ، خلبانان اتوماتیک برای هواپیماهای سرنشین دار به عنوان یک خطای ایمنی طراحی شده اند - یعنی هیچ نقصی در خلبان اتوماتیک نمی تواند از به کارگیری موثر لغو دستی جلوگیری کند. برای لغو کردن خلبان خودکار ، یکی از اعضای خدمه به سادگی باید سیستم را جدا کند ، یا با چرخاندن یک سوئیچ برق یا اگر این کار نمی کند ، با کشیدن قطع کننده مدار خلبان خودکار .
برخی از سقوط های هواپیما را مسئول شرایطی می دانند که خلبانان نتوانسته اند از سیستم کنترل پرواز خودکار جدا شوند. در پایان خلبانان با تنظیماتی که خلبان خودکار انجام می دهد مبارزه می کنند و نمی توانند بفهمند که چرا هواپیما همان کاری را که از آن خواسته اند انجام نمی دهد. به همین دلیل است که برنامه های آموزش پرواز فقط برای چنین سناریویی تمرین می کنند. خلبانان باید بدانند که چگونه از هر ویژگی AFCS استفاده کنند ، اما همچنین باید نحوه خاموش کردن و پرواز بدون آن را بدانند. آنها همچنین باید از یک برنامه دقیق نگهداری و تعمیرات پیروی کنند تا اطمینان حاصل کنند که همه سنسورها و سرووها از عملکرد خوبی برخوردار هستند. برای هرگونه تنظیم یا اصلاح در سیستم های کلیدی ممکن است نیاز به دستکاری خلبان اتوماتیک باشد. به عنوان مثال ، تغییری که در ابزارهای ژیروسکوپی ایجاد شده نیاز به تنظیم مجدد تنظیمات در خلبان اتوماتیک داردکامپیوتر .
نکته برای دانستن خلبان خودکار ، باید بدانید که هنگام پرواز ، یک هواپیما حدود سه محور را حرکت می دهد که X ، Y و Z یا محور جانبی ، محور طولی و محور عمودی است یا به عنوان Roll axis ، Pitch axis و Yaw شناخته می شود. سه سطح کنترل اساسی وجود دارد که می توان از خلبان توسط خلبان برای انتقال هواپیما به این محورها استفاده کرد. رول با حرکت Aileron کنترل می شود ، Pitch با حرکت آسانسور و Yaw با حرکت Rudder کنترل می شود. Pilot دارای یک میله کنترل یا یک چرخ کنترل برای کنترل هواپیماها و آسانسورها است در حالی که سکان با استفاده از پدال های سکان کنترل می شود. .
با دیدن اصول کنترل هواپیما ، به شما بگویم که در سیستم خلبان اتوماتیک ، این سطوح کنترل نیز می توانند توسط محرک های الکتریکی به صورت مکانیکی به میله های کنترل متصل شوند که ورودی خلبان را به سطح کنترل متصل می کنند. در حالی که در هوا هستید ، اگر یک خلبان هواپیما را به مسیر و ارتفاع دلخواه برساند و کنترل خود را ترک کند ، هواپیما به طور مداوم در همان حالت پرواز نمی کند بلکه به دلیل تلاطم ، رانش نامتقارن و غیره به آرامی از سر یا ارتفاع مورد نظر خود منحرف می شود. او باید به طور مداوم کنترل های خود را انجام دهد و هواپیما را در وضعیت مطلوب خود نگه دارد. اما با خلبان اتوماتیک ، اوضاع متفاوت است. این سیستم دارای سنسورهای مختلفی (به طور کلی ژیروسکوپ) است که برای ایجاد هرگونه اختلال در سه محور تعبیه شده است. آنها این ورودی ها را به صورت سیگنال های الکتریکی به کامپیوتر می دهند. رایانه تصمیم می گیرد كه كدام سطح كنترل شود تا چه اندازه این اختلال اصلاح شود و سیگنال را به محرك الكتریكی مناسب می فرستد همانطور كه قبلاً اشاره كردم. سطح کنترل حرکت می کند و هواپیما به حالت اولیه خود باز می گردد. باز هم سنسورهایی نصب شده اند که این حرکت اصلاحی هواپیما را گرفته و سیگنال های الکتریکی را به کامپیوتر می فرستند (گاهی اوقات محرک خود سیگنال بازخورد را می فرستد). سپس رایانه سیگنال اصلاح اصلی را قطع می کند. بنابراین محرک ها حرکت بیشتر کنترل ها را متوقف می کنند. این نمودار ساده را بررسی کنید.
به غیر از ورودی های سنسورها ، خلبان همچنین می تواند ورودی خود را از طریق واحد کنترل خلبان خودکار به کامپیوتر خلبان خودکار وارد کند. در این حالت خلبان خودکار هواپیما را مطابق ورودی های خلبان حرکت می دهد. در هر زمان خاص یا در مواقع اضطراری ، خلبان همیشه گزینه ای برای قطع خلبان اتوماتیک و گرفتن کنترل دارد.

- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: هوافضا
چگونه می توانیم تعیین کنیم که جریان در یک تونل باد به حالت پایدار می رسد؟من در حال بررسی جریان و انتقال حرارت روی یک سیلندر در یک تونل باد هستم. من میخواهم دادههایی را که برای محاسبه ویژگیهای جریان نیاز دارم، ثبت کنم، اما چگونه میتوانم مطمئن شوم که شرایط حالت پایدار به دست آمده است؟ تغییرات بسیار کمی در پارامترهای اندازه گیری شده مانند سرعت وجود دارد و ما می دانیم که در شرایط پایدار هیچ تغییری با زمان وجود ندارد.مشکل اصلی شما جریان هوای تونل باد نیست بلکه انتقال حرارت است.
به طور کلی جریان هوا در یک تونل باد می تواند خیلی سریع به حالت ثابت برسد (هم برای تونل های باد باز و هم برای تونل های بسته). با این حال، من معتقدم مشکل انتقال حرارت در سیلندر است.
بسته به اینکه آزمایش خود را چگونه تنظیم کنید، بستگی دارد.
به عنوان مثال، اگر از یک تونل باد باز استفاده می کنید، دمای هوا در طول روز در نوسان خواهد بود. این شیب انتقال حرارت را تغییر میدهد و شما (واقعاً) حالت ثابتی نخواهید داشت.
پارامتر دیگری که تأثیر میگذارد این است که سیلندر در داخل تا دمایی گرم شود یا اینکه بهطور بیحرکتی در آنجا قرار دارد. در حالت اول (حرارت داخلی) زمانی که دمای خارجی سیلندر برای تغییر دما متوقف می شود، حالت ثابتی خواهید داشت. از طرف دیگر (سیلندر گرم نشده) شما یک حالت ثابت خواهید داشت، زمانی که سیلندر در داخل دارای دمای یکسانی با هوای جاری در اطراف آن باشد.
همانطور که می بینید، تغییرات زیادی وجود دارد
تقریب حالت پایدار برای جریان سیال قابل تراکم (منیفولدها و سایر مخازن تحت فشار)
قبل از اینکه به تجزیه و تحلیل CFD روی بیاورم، در مورد یک سؤال / کلاس سؤالاتی که می خواهم از طریق تخمین تقریبی حل کنم، گیج شده ام.
بگو من یک مخزن فشار دارم با یک ورودی و یک خروجی. مخزن تحت فشار در مقداری فشار اولیه P0 قرار دارد. خروجی در مقداری فشار ثابت است. ورودی مقداری دبی جرمی دارد، m˙ (فرض کنید به یک مخزن بی نهایت بالادست و یک کنترل کننده جریان جرم متصل است).
با یک سیال قابل تراکم، سرعت جریان جرم مشخص، و حجم تنظیم شده در ظرف، از چه مکانیزمی برای تقریب فشار حالت پایدار نهایی (متوسط حجم، می گوییم) در ظرف استفاده می کنید؟ فرض کنید فشار خروجی به حدی باشد که جریان خفه شود. فرض کنید هیچ انتقال حرارتی به دیوارها وجود ندارد و گاز ایده آل است.
یکی از راه حل هایی که من به آن فکر کرده ام اجرای یک راه حل تکراری گنگ است:
یک مرحله زمانی را انتخاب کنید، dt
جرم m˙∗dt را به مخزن اضافه کنید
فشار جدید در مخزن را از طریق قانون گاز ایده آل محاسبه کنید
از معادله جریان لوله خفه شده برای تعیین m˙ در خروجی (دانستن منطقه خروجی) استفاده کنید.
جرم $\dot{m}_{exit} * dt$ را از مخزن کم کنید
تکرار تا "همگرایی"
احتمالاً میتوانید تحلیلی به سبک برنولی انجام دهید، اما من میخواهم این نوع تقریب را برای یک مسئله چند ورودی/چند خروجی نیز اعمال کنم. به نظر می رسد که نوعی از روش هاردی کراس نیز ممکن است قابل اجرا باشد. علاقه مند به پیشنهادات هر کسی.
نمودارهایی از آنچه تکنیک بالا برای سرعت جریان 1 کیلوگرم بر ثانیه به یک ظرف حجمی 5 متر 3، شرایط اولیه T = 290K و P = 1 Pa در ظرف به من می دهد:
همگرایی نرخ جریان جرمی
همگرایی فشار
ما سیستم را به سادگی برای دبی جرمی کوچک در مقایسه با اندازه به سادگی مدل می کنیم:
در نقطه 1، فشار می تواند نزدیک به بی نهایت باشد، یا چگالی می تواند نزدیک به بی نهایت باشد، یا به سادگی ظرفیت ممکن است نزدیک به بی نهایت باشد تا جایی که می توانیم بگوییم. در این مرحله، یک چیز به طور قطع مشخص است - مهم نیست که تنظیم کننده جریان جرمی به چه چیزی نیاز دارد، این سیستم انرژی کافی برای احساس نیاز دارد. با این حال، مخزن آن را در مقایسه با سایر نقاط، $h_1 \approx \infty$ تامین می کند. با این حال، از آنجایی که سرعت جریان جرمی نسبت به بقیه نسبتاً کوچک است، هر حذف جرم دمای مخزن را نسبتاً ثابت نگه میدارد. منصفانه است که بیان کنیم که T1=T، زیرا V1≈0. به هر حال، مخزن در مقایسه با مقدار کمی که از آن خارج میشود، آنقدر حجیم است که مخزن در مقایسه با مقداری که باقی مانده است، سیال را گرم یا خنک میکند، بنابراین بیرون h1 را ثابت نگه میدارد.
با دینامیک تنظیم کننده جریان جرمی، می دانیم که جرم m˙ از مخزن خارج می شود. ما چیز زیادی در مورد نقطه 2 نمی دانیم، اما کاملاً واضح است که $h_2 \lll h_1$اگر اینطور نبود، مخزن مورد نظر نمی توانست از طریق خط مورد نظر منبع انرژی و تامین انبوه ثابتی را تامین کند. فشار هنوز کاملاً ناشناخته است، اما $P_1 \ggg P_2 > P_3 \ggg P_4$، یا سیال اصلاً از سیستم خارج نمیشود. با این حال، در سراسر رگولاتور، حرکت جرم کوچک سیال در مقایسه با اندازه لولهکشی، عدد استانتون سیال را زیر سوال میبرد. در یک عدد استانتون بالا، میتوان نشان داد که گرمای زیادی از لوله به سیال برمیگردد و T2=T را دوباره برقرار میکند و h2 را بالا میآورد، اما کمتر از h1 از P2<P1
همانطور که در بالا مشخص شد، دمای T2 باید به دمای اتاق بازگردد. در حالی که انرژی ناشناخته است، ما در تلاش برای یافتن P3 هستیم. از آنجایی که وارد یک مخزن می شویم، V3≈0، و سیال راکد می شود. دیواره های مخزن ممکن است مایع داخل را گرم کنند. از آنجایی که دبی جرمی در مقایسه با جرم سیال داخل مخزن در حالت پایدار کم است، مشاهده می شود که مخزن باید سیال را تا زمانی که به T برسد گرم کند. بنابراین دمای راکد $T_{0_3} = T$است. با شناخته شدن این دما، معادله جریان خفه شده را می توان تغییر داد تا $P_{3_{final}}$ نهایی را نشان دهد، زیرا سیال راکد شده است:$\dot m = \dot m_{choked} = A_e(P_0 = P_3)\sqrt{\frac{k}{R(T_0 = T_3 = T)}}\left(\frac{2}{k+1}\right)^{\frac{k+1}{2(k-1)}}$
$P_{3_{final}} = \frac{\dot m}{A_e\sqrt{\frac{k}{RT}}\left(\frac{2}{k+1}\right)^{\frac{k+1}{2(k-1)}}}$
در واقع، با این مفروضات، شما عملاً مخزن را در نقطه 3 به تنظیم کننده جریان جرم خود تبدیل کرده اید، به قیمت ثابت نگه داشتن فشار و دمای داخل مخزن 3.
سوال جالبی است، اما ارزش بحث در مورد سردرگمی معادلات جریان تراکم پذیر را دارد. در حالت پایدار، ما همیشه سرعت جریان جرمی را ثابت خواهیم داشت، حتی با جریان خفه شده. سرعت جریان در خروجی باید با سرعت ورودی یکسان باشد. به نظر می رسد این غیر شهودی است - جریان خفه نشان می دهد که حداکثر سرعت جریانی وجود دارد که یک نازل می تواند تولید کند، و نه بیشتر. با این حال، حالات جریان خفه این مورد برای واریانس شرایط خروجی است، نرخ جریان افزایش نخواهد یافت. چیزی در مورد واریانس شرایط ورودی بیان نمی کند. در واقع، ایده اصلی پشت جریان خفه شده این است که به یک تکینگی در معادله دیفرانسیل (که بر اساس فرض نرخ جریان جرمی ثابت مشتق شده است) بستگی دارد:
$\frac{\partial V}{V} = -\frac{\partial A}{A}\frac{1}{1-M^2}$
اگر عدد ماخ دقیقاً 1 باشد، تغییر دیفرانسیل در مساحت باید 0 باشد، در غیر این صورت تغییر دیفرانسیل در سرعت بی نهایت خواهد بود! این باید در نازل خروجی کشتی شما باشد. با این حال، سناریوی پیشنهادی عمداً تلاش میکند تا جرم اضافی کشتی را از یک مخزن تحت فشار بینهایت بدون نازل همگرا/واگرا تغذیه کند.
اگر اطلاعات بیشتری در مورد جریان ورودی (مانند دما یا فشار) شناخته شده بود، میتوان این وضعیت را حل کرد. ما نمیتوانیم از ویژگیهای مخزن استفاده کنیم، زیرا مشخص نیست که دبیسنج جرمی چگونه بر جریان تأثیر میگذارد.
به طور کلی جریان هوا در یک تونل باد می تواند خیلی سریع به حالت ثابت برسد (هم برای تونل های باد باز و هم برای تونل های بسته). با این حال، من معتقدم مشکل انتقال حرارت در سیلندر است.
بسته به اینکه آزمایش خود را چگونه تنظیم کنید، بستگی دارد.
به عنوان مثال، اگر از یک تونل باد باز استفاده می کنید، دمای هوا در طول روز در نوسان خواهد بود. این شیب انتقال حرارت را تغییر میدهد و شما (واقعاً) حالت ثابتی نخواهید داشت.
پارامتر دیگری که تأثیر میگذارد این است که سیلندر در داخل تا دمایی گرم شود یا اینکه بهطور بیحرکتی در آنجا قرار دارد. در حالت اول (حرارت داخلی) زمانی که دمای خارجی سیلندر برای تغییر دما متوقف می شود، حالت ثابتی خواهید داشت. از طرف دیگر (سیلندر گرم نشده) شما یک حالت ثابت خواهید داشت، زمانی که سیلندر در داخل دارای دمای یکسانی با هوای جاری در اطراف آن باشد.
همانطور که می بینید، تغییرات زیادی وجود دارد
تقریب حالت پایدار برای جریان سیال قابل تراکم (منیفولدها و سایر مخازن تحت فشار)
قبل از اینکه به تجزیه و تحلیل CFD روی بیاورم، در مورد یک سؤال / کلاس سؤالاتی که می خواهم از طریق تخمین تقریبی حل کنم، گیج شده ام.
بگو من یک مخزن فشار دارم با یک ورودی و یک خروجی. مخزن تحت فشار در مقداری فشار اولیه P0 قرار دارد. خروجی در مقداری فشار ثابت است. ورودی مقداری دبی جرمی دارد، m˙ (فرض کنید به یک مخزن بی نهایت بالادست و یک کنترل کننده جریان جرم متصل است).
با یک سیال قابل تراکم، سرعت جریان جرم مشخص، و حجم تنظیم شده در ظرف، از چه مکانیزمی برای تقریب فشار حالت پایدار نهایی (متوسط حجم، می گوییم) در ظرف استفاده می کنید؟ فرض کنید فشار خروجی به حدی باشد که جریان خفه شود. فرض کنید هیچ انتقال حرارتی به دیوارها وجود ندارد و گاز ایده آل است.
یکی از راه حل هایی که من به آن فکر کرده ام اجرای یک راه حل تکراری گنگ است:
یک مرحله زمانی را انتخاب کنید، dt
جرم m˙∗dt را به مخزن اضافه کنید
فشار جدید در مخزن را از طریق قانون گاز ایده آل محاسبه کنید
از معادله جریان لوله خفه شده برای تعیین m˙ در خروجی (دانستن منطقه خروجی) استفاده کنید.
جرم $\dot{m}_{exit} * dt$ را از مخزن کم کنید
تکرار تا "همگرایی"
احتمالاً میتوانید تحلیلی به سبک برنولی انجام دهید، اما من میخواهم این نوع تقریب را برای یک مسئله چند ورودی/چند خروجی نیز اعمال کنم. به نظر می رسد که نوعی از روش هاردی کراس نیز ممکن است قابل اجرا باشد. علاقه مند به پیشنهادات هر کسی.
نمودارهایی از آنچه تکنیک بالا برای سرعت جریان 1 کیلوگرم بر ثانیه به یک ظرف حجمی 5 متر 3، شرایط اولیه T = 290K و P = 1 Pa در ظرف به من می دهد:
همگرایی نرخ جریان جرمی
همگرایی فشار
ما سیستم را به سادگی برای دبی جرمی کوچک در مقایسه با اندازه به سادگی مدل می کنیم:
در نقطه 1، فشار می تواند نزدیک به بی نهایت باشد، یا چگالی می تواند نزدیک به بی نهایت باشد، یا به سادگی ظرفیت ممکن است نزدیک به بی نهایت باشد تا جایی که می توانیم بگوییم. در این مرحله، یک چیز به طور قطع مشخص است - مهم نیست که تنظیم کننده جریان جرمی به چه چیزی نیاز دارد، این سیستم انرژی کافی برای احساس نیاز دارد. با این حال، مخزن آن را در مقایسه با سایر نقاط، $h_1 \approx \infty$ تامین می کند. با این حال، از آنجایی که سرعت جریان جرمی نسبت به بقیه نسبتاً کوچک است، هر حذف جرم دمای مخزن را نسبتاً ثابت نگه میدارد. منصفانه است که بیان کنیم که T1=T، زیرا V1≈0. به هر حال، مخزن در مقایسه با مقدار کمی که از آن خارج میشود، آنقدر حجیم است که مخزن در مقایسه با مقداری که باقی مانده است، سیال را گرم یا خنک میکند، بنابراین بیرون h1 را ثابت نگه میدارد.
با دینامیک تنظیم کننده جریان جرمی، می دانیم که جرم m˙ از مخزن خارج می شود. ما چیز زیادی در مورد نقطه 2 نمی دانیم، اما کاملاً واضح است که $h_2 \lll h_1$اگر اینطور نبود، مخزن مورد نظر نمی توانست از طریق خط مورد نظر منبع انرژی و تامین انبوه ثابتی را تامین کند. فشار هنوز کاملاً ناشناخته است، اما $P_1 \ggg P_2 > P_3 \ggg P_4$، یا سیال اصلاً از سیستم خارج نمیشود. با این حال، در سراسر رگولاتور، حرکت جرم کوچک سیال در مقایسه با اندازه لولهکشی، عدد استانتون سیال را زیر سوال میبرد. در یک عدد استانتون بالا، میتوان نشان داد که گرمای زیادی از لوله به سیال برمیگردد و T2=T را دوباره برقرار میکند و h2 را بالا میآورد، اما کمتر از h1 از P2<P1
همانطور که در بالا مشخص شد، دمای T2 باید به دمای اتاق بازگردد. در حالی که انرژی ناشناخته است، ما در تلاش برای یافتن P3 هستیم. از آنجایی که وارد یک مخزن می شویم، V3≈0، و سیال راکد می شود. دیواره های مخزن ممکن است مایع داخل را گرم کنند. از آنجایی که دبی جرمی در مقایسه با جرم سیال داخل مخزن در حالت پایدار کم است، مشاهده می شود که مخزن باید سیال را تا زمانی که به T برسد گرم کند. بنابراین دمای راکد $T_{0_3} = T$است. با شناخته شدن این دما، معادله جریان خفه شده را می توان تغییر داد تا $P_{3_{final}}$ نهایی را نشان دهد، زیرا سیال راکد شده است:$\dot m = \dot m_{choked} = A_e(P_0 = P_3)\sqrt{\frac{k}{R(T_0 = T_3 = T)}}\left(\frac{2}{k+1}\right)^{\frac{k+1}{2(k-1)}}$
$P_{3_{final}} = \frac{\dot m}{A_e\sqrt{\frac{k}{RT}}\left(\frac{2}{k+1}\right)^{\frac{k+1}{2(k-1)}}}$
در واقع، با این مفروضات، شما عملاً مخزن را در نقطه 3 به تنظیم کننده جریان جرم خود تبدیل کرده اید، به قیمت ثابت نگه داشتن فشار و دمای داخل مخزن 3.
سوال جالبی است، اما ارزش بحث در مورد سردرگمی معادلات جریان تراکم پذیر را دارد. در حالت پایدار، ما همیشه سرعت جریان جرمی را ثابت خواهیم داشت، حتی با جریان خفه شده. سرعت جریان در خروجی باید با سرعت ورودی یکسان باشد. به نظر می رسد این غیر شهودی است - جریان خفه نشان می دهد که حداکثر سرعت جریانی وجود دارد که یک نازل می تواند تولید کند، و نه بیشتر. با این حال، حالات جریان خفه این مورد برای واریانس شرایط خروجی است، نرخ جریان افزایش نخواهد یافت. چیزی در مورد واریانس شرایط ورودی بیان نمی کند. در واقع، ایده اصلی پشت جریان خفه شده این است که به یک تکینگی در معادله دیفرانسیل (که بر اساس فرض نرخ جریان جرمی ثابت مشتق شده است) بستگی دارد:
$\frac{\partial V}{V} = -\frac{\partial A}{A}\frac{1}{1-M^2}$
اگر عدد ماخ دقیقاً 1 باشد، تغییر دیفرانسیل در مساحت باید 0 باشد، در غیر این صورت تغییر دیفرانسیل در سرعت بی نهایت خواهد بود! این باید در نازل خروجی کشتی شما باشد. با این حال، سناریوی پیشنهادی عمداً تلاش میکند تا جرم اضافی کشتی را از یک مخزن تحت فشار بینهایت بدون نازل همگرا/واگرا تغذیه کند.
اگر اطلاعات بیشتری در مورد جریان ورودی (مانند دما یا فشار) شناخته شده بود، میتوان این وضعیت را حل کرد. ما نمیتوانیم از ویژگیهای مخزن استفاده کنیم، زیرا مشخص نیست که دبیسنج جرمی چگونه بر جریان تأثیر میگذارد.

- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: هوافضا
چرخه Brayton یک چرخه ترمودینامیکی است که نحوه عملکرد توربین های گازی را توصیف می کند. ایده موجود در چرخه Brayton استخراج انرژی از جریان هوا و سوخت برای تولید کار قابل استفاده است که می تواند با استفاده از رانش آنها برای تأمین انرژی بسیاری از وسایل نقلیه مورد استفاده قرار گیرد. اساسی ترین مراحل در استخراج انرژی ، فشرده سازی هوای جاری ، احتراق و سپس انبساط آن هوا برای ایجاد کار و همچنین تأمین فشار همزمان است. مفید بودن چرخه Brayton به دلیل اینکه ستون فقرات در رانندگی بسیاری از وسایل نقلیه مانند جت ها ، هلی کوپترها و حتی زیردریایی ها محسوب می شود ، فوق العاده است.
سیکل برایتون است چرخه ترمودینامیکی مورد استفاده در برخی موتورهای حرارتی . قابل ذکر است که برای موتورهای توربین گازی و برخی موتورهای جت استفاده می شود. این چرخه شامل فشرده سازی هوای محیط ، مخلوط کردن هوا با سوخت و سپس احتراق مخلوط است که منبسط می شود و کار می کند. سپس در بسیاری از موتورهای چرمی برایتون می توان هوای گرم را بازیافت کرد و هوای تازه را از طریق آن گرم کرد. این کارایی را افزایش می دهد ، زیرا برای گرم کردن هوای تازه به سوخت کمتری نیاز است. از نظر فیزیک، این دوره از آدیاباتیک فشرده سازی و گسترش زوج با هم فشار گرمایش و سرمایش، و اجازه می دهد تا برای افزایش بهره وری بیش از برخی از چرخه های دیگر است.
اولین توربین گازی که چرخه Brayton را اجرا کرد (البته با اطلاع نیست ، زیرا قبل از تاسیس چرخه Brayton ایجاد شده بود) توربین گازی جان باربر بود که در سال 179 ثبت اختراع شد. ایده ماشین فشرده سازی هوای جو در یک محفظه و سوخت بود در یک اتاق دیگر و هر دو اتاق به یک ظرف احتراق متصل می شوند. هنگامی که هوا با سوخت مخلوط شده و واکنش نشان داد ، انرژی حاصل از احتراق برای چرخاندن توربین برای انجام کار مفید استفاده می شود. با این حال ، از آنجا که در اواخر قرن هجدهم پیشرفتهای فنی وجود نداشت ، توربین گاز انرژی کافی برای فشار دادن گازها و انجام کارهای مفید در همان زمان را نداشت ، بنابراین از آن استفاده نشد.
جورج برایتون مهندسی بود که اولین موتور احتراق مداوم با احتراق را طراحی کرد که یک موتور دو زمانه بود و با نام "Brayton's Ready Motors" فروخته شد. این طرح از فرآیندهای ترمودینامیکی استفاده می کند که اکنون "چرخه برایتون" در نظر گرفته می شود ، اما همچنین چرخه ژول نیز ساخته شده است. این توربین گازی در سال 1872 ثبت اختراع شد. این طراحی یک موتور متصل به مخزن هوای جو تحت فشار و گاز بود که فقط در صورت روشن شدن سوپاپ روشن می شود. این می تواند گاز تحت فشار را به یک ظرف احتراق آزاد کند ، که پیستون ها را برای ایجاد کار مکانیکی و فشرده سازی مجدد گاز در مخزن تبدیل می کند.
(1) هوای محیطی در جو که در حال حاضر آشفته نیست.
(1 -> 2) هوای محیط با کمپرسور توربین گاز تماس پیدا می کند و فشار و دما بطور چشمگیری افزایش می یابد. افزایش فشار ناشی از کار هوا توسط کمپرسور است که هوا را به داخل میکسر / محفظه احتراق بسته بندی می کند و افزایش فشار باعث افزایش دما در مولکول های گاز می شود زیرا حجم مخزن ثابت می ماند (PV = nRT ) از آنجا که این یک فرایند ایده آل است ، اعتقاد بر این است که آنتروپی ثابت می ماند ، بنابراین این یک روند ایزنتروپیک است (در حقیقت ، آنتروپی به دلیل جریان و حرکت مولکول های گاز افزایش می یابد).
(3 -> 5) هوای جوی در محفظه احتراق فشرده شده است و در آن سوخت گاز با هوا مخلوط می شود. هنگامی که این مخلوط مشتعل شد ، شاهد افزایش شدید دما و آنتروپی هستیم (نه فشار ، زیرا منحنی ها مقدار خاصی از فشار را نشان می دهند ، بنابراین این یک فرآیند ایزوباریک است ) به دلیل واکنش احتراق سوخت و هوا . انرژی حاصل از پیوندهای شیمیایی موجود در سوخت به دلیل اشتعال شکسته می شود و یک واکنش بسیار گرمازا رخ می دهد که باعث افزایش آنتروپی به دلیل شکستن زنجیره های هیدروکربن به آب و هوا (مولکول های بیشتر) و افزایش دما به دلیل افزایش انرژی محیط از واکنش گرمازا.
(5 -> در نقطه 5 ، سوخت و هوا تحت فشار محفظه احتراق را به محفظه انبساط ترک می کند ، جایی که به دلیل حجم بیشتر و قرار گرفتن در معرض محیط شاهد افت سریع فشار هستیم. انرژی حاصل از محفظه احتراق به دو منظور مورد استفاده قرار می گیرد: چرخاندن توربینی که به کمپرسور متصل است (که چرخه Brayton را به طور مداوم روشن نگه می دارد) و به عنوان رانش. این دو هدف نشان دهنده نقطه 6 است و در حالت ایده آل یک فرایند ایزنتروپیک است. افت سریع فشار نشان می دهد که چگونه انرژی موجود در هوا در احتراق به صورت مکانیکی برای چرخاندن توربی که فرایند کمپرسور را اجرا می کند استفاده می شود زیرا انرژی لازم برای فشرده سازی انرژی اتمسفر کمتر از انرژی تولید شده توسط احتراق است. سوخت انرژی باقیمانده از چرخش توربین به عنوان رانش برای انجام کار استفاده می شود (مانند پرواز با جت). هوای دفع شده سپس به هوای محیطی تبدیل می شود که دارای سطح انرژی بالاتری نسبت به هوای نقطه 1 است ، اما در نهایت انرژی خود را به اطراف از دست می دهد (
در نقطه 5 ، سوخت و هوا تحت فشار محفظه احتراق را به محفظه انبساط ترک می کند ، جایی که به دلیل حجم بیشتر و قرار گرفتن در معرض محیط شاهد افت سریع فشار هستیم. انرژی حاصل از محفظه احتراق به دو منظور مورد استفاده قرار می گیرد: چرخاندن توربینی که به کمپرسور متصل است (که چرخه Brayton را به طور مداوم روشن نگه می دارد) و به عنوان رانش. این دو هدف نشان دهنده نقطه 6 است و در حالت ایده آل یک فرایند ایزنتروپیک است. افت سریع فشار نشان می دهد که چگونه انرژی موجود در هوا در احتراق به صورت مکانیکی برای چرخاندن توربی که فرایند کمپرسور را اجرا می کند استفاده می شود زیرا انرژی لازم برای فشرده سازی انرژی اتمسفر کمتر از انرژی تولید شده توسط احتراق است. سوخت انرژی باقیمانده از چرخش توربین به عنوان رانش برای انجام کار استفاده می شود (مانند پرواز با جت). هوای دفع شده سپس به هوای محیطی تبدیل می شود که دارای سطح انرژی بالاتری نسبت به هوای نقطه 1 است ، اما در نهایت انرژی خود را به اطراف از دست می دهد (
IBC = چرخه برایتون معکوس
در روند توربین گاز میکرو معکوس ، جریان اجزای منفرد در توالی متفاوتی از چرخه MGT معمولی (چرخه Brayton) رخ می دهد. شکل 2 را ببینید. در یک IBC-MGT ، هوای فرآیند مستقیماً وارد رکابیتور (2) می شود ، گرم می شود و به محفظه احتراق منتقل می شود ، جایی که با سوخت مخلوط می شود و می سوزد (3). پس از خروج از محفظه احتراق ، گاز خروجی از طریق توربین هدایت می شود و در آنجا زیر فشار محیط منبسط می شود (4). متعاقباً ، ابتدا گاز خروجی قبل از اینکه در فشار اتمسفر در کمپرسور فشرده شود ، در رکابیتور (2) و سپس در مبدل حرارتی آب پایین دست (5) خنک می شود. در این چرخه معکوس - مانند یک چرخه معمولی ، توربین دوباره انرژی بیشتری از آنچه برای فرایند فشرده سازی مورد نیاز است ، تولید می کند ، بنابراین می توان یک ژنراتور (6) را کار کرد.در نتیجه فشرده سازی ، گاز خروجی گرم می شود و بنابراین می تواند در مبدل حرارتی آب دوم (7) دوباره خنک شود تا از انرژی آزاد شده تا حد امکان بهره برداری شود.
1برای یافتن کارایی چرخه Brayton ، باید بدانیم که هر فرآیند چقدر به کل انرژی داخلی کمک می کند. ما برای انجام این کار نمودار PV بالا را تجزیه و تحلیل خواهیم کرد.$ U = q_1 + q_2 - w = 0$
s برابر با صفر است زیرا قانون اول ترمودینامیک بیان می کند که انرژی از بین نمی رود یا ایجاد نمی شود و زیرا در چرخه برایتون عملکرد نهایی گاز اولیه است ، U = 0.
این یعنی$w = q_1 + q_2 $که در آن q1 گرمای دریافت شده توسط احتراق است (بنابراین منفی است) و q2 گرمای آزاد شده پس از انبساط است.
اگر شما گاز را به عنوان یک گاز کامل با گرماهای خاص ثابت در نظر بگیرید ، می توانیم مقدار گرمایی حاصل از احتراق را ببینیم$q_1 = c_p(T_I - T_F) $, و $q_2 = c_p(T_F - T_I) $
جایی که TF دمای نهایی احتراق یا قسمت "گرمای از دست رفته در اتمسفر" است و دومی اولیه است. (بنابراین در منحنی PV ، فرایند احتراق$ q_1 = c_p(T_4 - T_3)$ خواهد داشت
بنابراین اکنون مقدار گرمای از دست رفته و به دست آمده را از نظر دما بیان کردیم ، می توانیم معادله را دوباره پیدا کنیم تا eta (بازده حرارتی) را پیدا کنیم
$\eta = \dfrac{\textrm{Net work}}{\textrm{Heat in}} = \dfrac{c_p[(T_c -T_c) - (T_d - T_a)]}{c_p(T_[T_c = T_b]} = 1 - \frac{(T_d-T_a)}{(T_c-T_b)} = 1 - \frac{T_a(T_d/T_a-1)}{T_b(T_c/T_b-1)}. $
من یک چرخه برایتون دارم و می خواهم بازده و نسبت کار برگشت را محاسبه کنم. در کتاب درسی من آمده است که گرمای اضافه شده در فرآیند 3-4 در فشار ثابت اتفاق می افتد (ایزوباریک) و بنابراین می توانیم . همچنین گفته شده است که این نتیجه از طریق اولین قانون ترمودینامیک با استفاده از معادله جریان پایدار محاسبه می شود: سپس آنها توجه دارند که می توانیم فرض کنیم و . حال س theال این است که من هیچ سرنخی ندارم که چگونه آنها نتیجه این معادله را پیدا می کنند. فکر می کنم بتوانیم بنویسیم:سیک ددE د=
$\dot{m}(h_3+\frac{C_3^2}{2} + Z_3g)+\dot{Q}+\dot{W}=\dot{m}(h_4+\frac{C_4^2}{2} + Z_4g) $و $\dot{Q}+\dot{W}=\dot{m}(h_4-h_3) $ همچنین $ q+w=h_4-h_3$ پس مینوان نوشت $w=-\int_{V_3}^{V_4}p dv = -p\int_{V_3}^{V_4}dv=-p[V_4-V_3] $ و $ q=h_4+pV_4-[h_3+pV_3]$
0آیا می دانید W در نسخه سیستم باز قانون اول ترمودینامیک همه کارها را شامل نمی شود ، بلکه فقط شافت را کار می کند؟ این کار انجام شده برای فشار دادن مایع به داخل و خارج از حجم کنترل نیست. دومی به طور جداگانه در ساعت ها گنجانده شده است. در مبادله حرارتی که شما آنالیز می کنید ، کار شافت صفر است. بنابراین گرمای اضافه شده در واحد جرم فقط با تغییر آنتالپی خاص بین ورودی و خروجی مبدل برابر است.
آیا وقتی آنها در مورد نسخه سیستم باز قانون 1 به شما آموختند ، این اطلاعات مهم پوشش داده نشد؟همه چیزهایی که می گویید درست است تا زمانی که جایگزین شوید w = ∫Pdv. این فرمول نشان دهنده کار مرزی برای سیستم های بسته است. هر یک از دستگاه های موجود در چرخه Brayton (کمپرسور ، توربین ، دو مبدل حرارتی) یک سیستم باز است.
روش استاندارد برای چرخه Brayton این است كه فرض كنید q = 0 در كمپرسور و توربین (به دلیل عایق بودن خوب و / یا انبساط / فشرده سازی نسبت به انتقال گرما سریع است) و w = 0 در مبدل های حرارتی ( زیرا هیچ محور چرخان ، پیستون یا سایر دستگاه هایی وجود ندارد که بتواند روی مواد جریان یافته در دستگاه کار کند).
ایجاد تعویض w = 0 نتیجه مطلوبی را به شما می دهد.
کارایی سیکل برایتون $\eta = \frac{C_p(T_3-T_4) - C_p(T_2-T_1)}{C_p(T_3-T_2)} $ چون $dQ_roham = C_p dT + pdV $و $Q_roham = C_p(T_3-T_2) + p_{max}(V_3-V_2) $
چرخه Brayton (یا چرخه ژول) نشان دهنده عملکرد یک موتور توربین گاز است.
برای عملکرد توربین گاز ، روند ثابت افزودن حرارت فشار ثابت ایده آل سازی فرآیند احتراق است. هیچ کار حجم فشار درگیر نیست
روند استخراج گرما با فشار ثابت به راحتی هوا را به حالت اولیه خود خنک می کند. در واقع یک خازن است. باز هم هیچ کاری در زمینه فشار وجود ندارد.
در انتها ، فرآیندهای فشار ثابت اساساً فرآیندهای تبادل گرما هستند$Q=C_{p}\Delta T$
بیان بازده حرارتی برای یک چرخه بسته Brayton از نظر آنتالپی های ساکن
که در آن c دمای نهایی فرآیند احتراق و b دمای اولیه قبل از احتراق و a دمای اولیه گاز بدون مزاحمت و d دمای گاز پس از دفع آن است. اعداد مربوط به حروف از نمودار PV a = 2 است. b = 3 ؛ c = 4 ؛ d = 6
هرچه نسبت دما کوچکتر باشد ، بازده چرخه Braytons بالاتر است. بنابراین ، هرچه گرمای بیشتری به سیستم وارد شود و مقدار کمتری از گرمای اتمسفر از بین برود ، نسبت دما را به میزان قابل توجهی کاهش داده و درصد کارایی بالاتری خواهد داشت.
من یک چرخه Brayton دارم که از کمپرسور (مرحله 2 تا 3) ، مبدل حرارتی (مرحله 3 تا 4) و توربین (مرحله 4 تا 5) ساخته شده است. توربین و کمپرسور از طریق یک شافت متصل می شوند. چرخه از طریق مبدل حرارتی بسته می شود ، جایی که هوای چرخشی داغ خنک می شود. در اینجا یک تصویر وجود دارد:
$\eta_{th}=\dfrac{\dot{W}_{net}}{\dot{Q}_{in}} $ و $\eta_{th}=1-\dfrac{h^{\prime}_5-h_2}{h_4-h^{\prime}_3} $سعی کردم از عبارت عمومی برای صرفه جویی در انرژی برای یک حجم کنترل (ثابت) (CV) استفاده کنم:$ 0=\dot{Q}_\text{CV}-\dot{W}_\text{CV}+\dot{m}_\text{in}\left(h_\text{in}+\frac{v_\text{in}^2}{2}\right)-\dot{m}_\text{out}\left(h_\text{out}+\frac{v_\text{out}^2}{2}\right)$
Q˙CV سرعت انتقال حرارت بیش از مرز CV است.
W˙cv انتقال انرژی توسط کار در آن سوی مرز حجم کنترل است.
به عنوان مثال می توانم این فرمول را روی کمپرسور اعمال کنم و موارد زیر را دریافت می کنم:
شما باید قانون اول را در مورد مبدل حرارتی کمپرسور ، توربین و دمای بالا بررسی کنید.
اگر کمپرسور و توربین ایده آل هستند ، ما باید موارد زیر را داشته باشیم:
قانون اول برای کمپرسور: wc=h2−h′3
قانون اول مبدل حرارتی با درجه حرارت بالا: $ q_{in}=h_4-h'_3$
قانون اول توربین: $w_t=h_4-h'_5$
خوب با توجه $ \large{\eta_{th}}=\large{\frac{w_{net}}{q_{in}}}$ دارم $w_{net}=w_t+w_c=h_4-h'_5+h_2-h'_3=(h_4-h'_3)-(h'_5-h_2) $ پس کحاسبه میشه $ \Longrightarrow\;\large{\eta_{th}}=\large{\frac{(h_4-h'_3)-(h'_5-h_2)}{h_4-h'_3}}=1-\large{\frac{h'_5-h_2}{h_4-h'_3}}$

توربین های گازی با استفاده از چرخه Brayton مدل سازی می شوند که در ساده ترین حالت از موارد زیر تشکیل می شود:
فشرده سازی ایزنتروپیک (در کمپرسور)
اضافه شدن گرما با فشار ثابت (محفظه احتراق)
انبساط ایزنتروپیک (در یک توربین)
و از آنجا که بهره وری به عنوان خروجی خالص / ورودی گرما تعریف می شود ، می توان به راحتی به عنوان زیر مربوط به دمای حالت های چرخه شد:
فرایندهای 1-2 و 3-4 ایزنتروپیک هستند و P2 = P3 و P4 = P1. بدین ترتیب:
و سرانجام بازده می تواند به نسبت فشرده سازی مربوط باشد به شرح زیر:
با این وجود بیشتر توربین های گازی در این شرایط ایده آل ساده نظیر فشرده سازی و انبساط ایزنتروپیک ، افزودن حرارت فشار ثابت ، فشرده سازی تک مرحله ای و انبساط تک مرحله ای کار نمی کنند. و در چنین مواردی مدل سازی و تجزیه و تحلیل کارایی بسیار پیچیده تر از چرخه ایده آل است.
سیکل برایتون است چرخه ترمودینامیکی مورد استفاده در برخی موتورهای حرارتی . قابل ذکر است که برای موتورهای توربین گازی و برخی موتورهای جت استفاده می شود. این چرخه شامل فشرده سازی هوای محیط ، مخلوط کردن هوا با سوخت و سپس احتراق مخلوط است که منبسط می شود و کار می کند. سپس در بسیاری از موتورهای چرمی برایتون می توان هوای گرم را بازیافت کرد و هوای تازه را از طریق آن گرم کرد. این کارایی را افزایش می دهد ، زیرا برای گرم کردن هوای تازه به سوخت کمتری نیاز است. از نظر فیزیک، این دوره از آدیاباتیک فشرده سازی و گسترش زوج با هم فشار گرمایش و سرمایش، و اجازه می دهد تا برای افزایش بهره وری بیش از برخی از چرخه های دیگر است.
اولین توربین گازی که چرخه Brayton را اجرا کرد (البته با اطلاع نیست ، زیرا قبل از تاسیس چرخه Brayton ایجاد شده بود) توربین گازی جان باربر بود که در سال 179 ثبت اختراع شد. ایده ماشین فشرده سازی هوای جو در یک محفظه و سوخت بود در یک اتاق دیگر و هر دو اتاق به یک ظرف احتراق متصل می شوند. هنگامی که هوا با سوخت مخلوط شده و واکنش نشان داد ، انرژی حاصل از احتراق برای چرخاندن توربین برای انجام کار مفید استفاده می شود. با این حال ، از آنجا که در اواخر قرن هجدهم پیشرفتهای فنی وجود نداشت ، توربین گاز انرژی کافی برای فشار دادن گازها و انجام کارهای مفید در همان زمان را نداشت ، بنابراین از آن استفاده نشد.
جورج برایتون مهندسی بود که اولین موتور احتراق مداوم با احتراق را طراحی کرد که یک موتور دو زمانه بود و با نام "Brayton's Ready Motors" فروخته شد. این طرح از فرآیندهای ترمودینامیکی استفاده می کند که اکنون "چرخه برایتون" در نظر گرفته می شود ، اما همچنین چرخه ژول نیز ساخته شده است. این توربین گازی در سال 1872 ثبت اختراع شد. این طراحی یک موتور متصل به مخزن هوای جو تحت فشار و گاز بود که فقط در صورت روشن شدن سوپاپ روشن می شود. این می تواند گاز تحت فشار را به یک ظرف احتراق آزاد کند ، که پیستون ها را برای ایجاد کار مکانیکی و فشرده سازی مجدد گاز در مخزن تبدیل می کند.
(1) هوای محیطی در جو که در حال حاضر آشفته نیست.
(1 -> 2) هوای محیط با کمپرسور توربین گاز تماس پیدا می کند و فشار و دما بطور چشمگیری افزایش می یابد. افزایش فشار ناشی از کار هوا توسط کمپرسور است که هوا را به داخل میکسر / محفظه احتراق بسته بندی می کند و افزایش فشار باعث افزایش دما در مولکول های گاز می شود زیرا حجم مخزن ثابت می ماند (PV = nRT ) از آنجا که این یک فرایند ایده آل است ، اعتقاد بر این است که آنتروپی ثابت می ماند ، بنابراین این یک روند ایزنتروپیک است (در حقیقت ، آنتروپی به دلیل جریان و حرکت مولکول های گاز افزایش می یابد).
(3 -> 5) هوای جوی در محفظه احتراق فشرده شده است و در آن سوخت گاز با هوا مخلوط می شود. هنگامی که این مخلوط مشتعل شد ، شاهد افزایش شدید دما و آنتروپی هستیم (نه فشار ، زیرا منحنی ها مقدار خاصی از فشار را نشان می دهند ، بنابراین این یک فرآیند ایزوباریک است ) به دلیل واکنش احتراق سوخت و هوا . انرژی حاصل از پیوندهای شیمیایی موجود در سوخت به دلیل اشتعال شکسته می شود و یک واکنش بسیار گرمازا رخ می دهد که باعث افزایش آنتروپی به دلیل شکستن زنجیره های هیدروکربن به آب و هوا (مولکول های بیشتر) و افزایش دما به دلیل افزایش انرژی محیط از واکنش گرمازا.
(5 ->
IBC = چرخه برایتون معکوس
در روند توربین گاز میکرو معکوس ، جریان اجزای منفرد در توالی متفاوتی از چرخه MGT معمولی (چرخه Brayton) رخ می دهد. شکل 2 را ببینید. در یک IBC-MGT ، هوای فرآیند مستقیماً وارد رکابیتور (2) می شود ، گرم می شود و به محفظه احتراق منتقل می شود ، جایی که با سوخت مخلوط می شود و می سوزد (3). پس از خروج از محفظه احتراق ، گاز خروجی از طریق توربین هدایت می شود و در آنجا زیر فشار محیط منبسط می شود (4). متعاقباً ، ابتدا گاز خروجی قبل از اینکه در فشار اتمسفر در کمپرسور فشرده شود ، در رکابیتور (2) و سپس در مبدل حرارتی آب پایین دست (5) خنک می شود. در این چرخه معکوس - مانند یک چرخه معمولی ، توربین دوباره انرژی بیشتری از آنچه برای فرایند فشرده سازی مورد نیاز است ، تولید می کند ، بنابراین می توان یک ژنراتور (6) را کار کرد.در نتیجه فشرده سازی ، گاز خروجی گرم می شود و بنابراین می تواند در مبدل حرارتی آب دوم (7) دوباره خنک شود تا از انرژی آزاد شده تا حد امکان بهره برداری شود.
1برای یافتن کارایی چرخه Brayton ، باید بدانیم که هر فرآیند چقدر به کل انرژی داخلی کمک می کند. ما برای انجام این کار نمودار PV بالا را تجزیه و تحلیل خواهیم کرد.$ U = q_1 + q_2 - w = 0$
s برابر با صفر است زیرا قانون اول ترمودینامیک بیان می کند که انرژی از بین نمی رود یا ایجاد نمی شود و زیرا در چرخه برایتون عملکرد نهایی گاز اولیه است ، U = 0.
این یعنی$w = q_1 + q_2 $که در آن q1 گرمای دریافت شده توسط احتراق است (بنابراین منفی است) و q2 گرمای آزاد شده پس از انبساط است.
اگر شما گاز را به عنوان یک گاز کامل با گرماهای خاص ثابت در نظر بگیرید ، می توانیم مقدار گرمایی حاصل از احتراق را ببینیم$q_1 = c_p(T_I - T_F) $, و $q_2 = c_p(T_F - T_I) $
جایی که TF دمای نهایی احتراق یا قسمت "گرمای از دست رفته در اتمسفر" است و دومی اولیه است. (بنابراین در منحنی PV ، فرایند احتراق$ q_1 = c_p(T_4 - T_3)$ خواهد داشت
بنابراین اکنون مقدار گرمای از دست رفته و به دست آمده را از نظر دما بیان کردیم ، می توانیم معادله را دوباره پیدا کنیم تا eta (بازده حرارتی) را پیدا کنیم
$\eta = \dfrac{\textrm{Net work}}{\textrm{Heat in}} = \dfrac{c_p[(T_c -T_c) - (T_d - T_a)]}{c_p(T_[T_c = T_b]} = 1 - \frac{(T_d-T_a)}{(T_c-T_b)} = 1 - \frac{T_a(T_d/T_a-1)}{T_b(T_c/T_b-1)}. $
من یک چرخه برایتون دارم و می خواهم بازده و نسبت کار برگشت را محاسبه کنم. در کتاب درسی من آمده است که گرمای اضافه شده در فرآیند 3-4 در فشار ثابت اتفاق می افتد (ایزوباریک) و بنابراین می توانیم . همچنین گفته شده است که این نتیجه از طریق اولین قانون ترمودینامیک با استفاده از معادله جریان پایدار محاسبه می شود: سپس آنها توجه دارند که می توانیم فرض کنیم و . حال س theال این است که من هیچ سرنخی ندارم که چگونه آنها نتیجه این معادله را پیدا می کنند. فکر می کنم بتوانیم بنویسیم:سیک ددE د=
$\dot{m}(h_3+\frac{C_3^2}{2} + Z_3g)+\dot{Q}+\dot{W}=\dot{m}(h_4+\frac{C_4^2}{2} + Z_4g) $و $\dot{Q}+\dot{W}=\dot{m}(h_4-h_3) $ همچنین $ q+w=h_4-h_3$ پس مینوان نوشت $w=-\int_{V_3}^{V_4}p dv = -p\int_{V_3}^{V_4}dv=-p[V_4-V_3] $ و $ q=h_4+pV_4-[h_3+pV_3]$
0آیا می دانید W در نسخه سیستم باز قانون اول ترمودینامیک همه کارها را شامل نمی شود ، بلکه فقط شافت را کار می کند؟ این کار انجام شده برای فشار دادن مایع به داخل و خارج از حجم کنترل نیست. دومی به طور جداگانه در ساعت ها گنجانده شده است. در مبادله حرارتی که شما آنالیز می کنید ، کار شافت صفر است. بنابراین گرمای اضافه شده در واحد جرم فقط با تغییر آنتالپی خاص بین ورودی و خروجی مبدل برابر است.
آیا وقتی آنها در مورد نسخه سیستم باز قانون 1 به شما آموختند ، این اطلاعات مهم پوشش داده نشد؟همه چیزهایی که می گویید درست است تا زمانی که جایگزین شوید w = ∫Pdv. این فرمول نشان دهنده کار مرزی برای سیستم های بسته است. هر یک از دستگاه های موجود در چرخه Brayton (کمپرسور ، توربین ، دو مبدل حرارتی) یک سیستم باز است.
روش استاندارد برای چرخه Brayton این است كه فرض كنید q = 0 در كمپرسور و توربین (به دلیل عایق بودن خوب و / یا انبساط / فشرده سازی نسبت به انتقال گرما سریع است) و w = 0 در مبدل های حرارتی ( زیرا هیچ محور چرخان ، پیستون یا سایر دستگاه هایی وجود ندارد که بتواند روی مواد جریان یافته در دستگاه کار کند).
ایجاد تعویض w = 0 نتیجه مطلوبی را به شما می دهد.
کارایی سیکل برایتون $\eta = \frac{C_p(T_3-T_4) - C_p(T_2-T_1)}{C_p(T_3-T_2)} $ چون $dQ_roham = C_p dT + pdV $و $Q_roham = C_p(T_3-T_2) + p_{max}(V_3-V_2) $
چرخه Brayton (یا چرخه ژول) نشان دهنده عملکرد یک موتور توربین گاز است.
برای عملکرد توربین گاز ، روند ثابت افزودن حرارت فشار ثابت ایده آل سازی فرآیند احتراق است. هیچ کار حجم فشار درگیر نیست
روند استخراج گرما با فشار ثابت به راحتی هوا را به حالت اولیه خود خنک می کند. در واقع یک خازن است. باز هم هیچ کاری در زمینه فشار وجود ندارد.
در انتها ، فرآیندهای فشار ثابت اساساً فرآیندهای تبادل گرما هستند$Q=C_{p}\Delta T$
بیان بازده حرارتی برای یک چرخه بسته Brayton از نظر آنتالپی های ساکن
که در آن c دمای نهایی فرآیند احتراق و b دمای اولیه قبل از احتراق و a دمای اولیه گاز بدون مزاحمت و d دمای گاز پس از دفع آن است. اعداد مربوط به حروف از نمودار PV a = 2 است. b = 3 ؛ c = 4 ؛ d = 6
هرچه نسبت دما کوچکتر باشد ، بازده چرخه Braytons بالاتر است. بنابراین ، هرچه گرمای بیشتری به سیستم وارد شود و مقدار کمتری از گرمای اتمسفر از بین برود ، نسبت دما را به میزان قابل توجهی کاهش داده و درصد کارایی بالاتری خواهد داشت.
من یک چرخه Brayton دارم که از کمپرسور (مرحله 2 تا 3) ، مبدل حرارتی (مرحله 3 تا 4) و توربین (مرحله 4 تا 5) ساخته شده است. توربین و کمپرسور از طریق یک شافت متصل می شوند. چرخه از طریق مبدل حرارتی بسته می شود ، جایی که هوای چرخشی داغ خنک می شود. در اینجا یک تصویر وجود دارد:
$\eta_{th}=\dfrac{\dot{W}_{net}}{\dot{Q}_{in}} $ و $\eta_{th}=1-\dfrac{h^{\prime}_5-h_2}{h_4-h^{\prime}_3} $سعی کردم از عبارت عمومی برای صرفه جویی در انرژی برای یک حجم کنترل (ثابت) (CV) استفاده کنم:$ 0=\dot{Q}_\text{CV}-\dot{W}_\text{CV}+\dot{m}_\text{in}\left(h_\text{in}+\frac{v_\text{in}^2}{2}\right)-\dot{m}_\text{out}\left(h_\text{out}+\frac{v_\text{out}^2}{2}\right)$
Q˙CV سرعت انتقال حرارت بیش از مرز CV است.
W˙cv انتقال انرژی توسط کار در آن سوی مرز حجم کنترل است.
به عنوان مثال می توانم این فرمول را روی کمپرسور اعمال کنم و موارد زیر را دریافت می کنم:
شما باید قانون اول را در مورد مبدل حرارتی کمپرسور ، توربین و دمای بالا بررسی کنید.
اگر کمپرسور و توربین ایده آل هستند ، ما باید موارد زیر را داشته باشیم:
قانون اول برای کمپرسور: wc=h2−h′3
قانون اول مبدل حرارتی با درجه حرارت بالا: $ q_{in}=h_4-h'_3$
قانون اول توربین: $w_t=h_4-h'_5$
خوب با توجه $ \large{\eta_{th}}=\large{\frac{w_{net}}{q_{in}}}$ دارم $w_{net}=w_t+w_c=h_4-h'_5+h_2-h'_3=(h_4-h'_3)-(h'_5-h_2) $ پس کحاسبه میشه $ \Longrightarrow\;\large{\eta_{th}}=\large{\frac{(h_4-h'_3)-(h'_5-h_2)}{h_4-h'_3}}=1-\large{\frac{h'_5-h_2}{h_4-h'_3}}$

توربین های گازی با استفاده از چرخه Brayton مدل سازی می شوند که در ساده ترین حالت از موارد زیر تشکیل می شود:
فشرده سازی ایزنتروپیک (در کمپرسور)
اضافه شدن گرما با فشار ثابت (محفظه احتراق)
انبساط ایزنتروپیک (در یک توربین)
و از آنجا که بهره وری به عنوان خروجی خالص / ورودی گرما تعریف می شود ، می توان به راحتی به عنوان زیر مربوط به دمای حالت های چرخه شد:
فرایندهای 1-2 و 3-4 ایزنتروپیک هستند و P2 = P3 و P4 = P1. بدین ترتیب:
و سرانجام بازده می تواند به نسبت فشرده سازی مربوط باشد به شرح زیر:
با این وجود بیشتر توربین های گازی در این شرایط ایده آل ساده نظیر فشرده سازی و انبساط ایزنتروپیک ، افزودن حرارت فشار ثابت ، فشرده سازی تک مرحله ای و انبساط تک مرحله ای کار نمی کنند. و در چنین مواردی مدل سازی و تجزیه و تحلیل کارایی بسیار پیچیده تر از چرخه ایده آل است.

- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: هوافضا
پیشرانه موشکی
پیشرانه است که به وسیله آن نیرویی برای تغییر سرعت یک وسیله نقلیه اعمال می شود و هم سرعت آن و هم جهت آن را تحت تأثیر قرار می ده. رانش وارد شده به یک موشک به دلیل واکنش ناشی از حرکت یک جت پرسرعت است که در خلاف جهت شتاب گیری و البته.توجه کنید رانش متناسب با محصول دبی جریان جرم است ،، و سرعت ، V جت (یعنی) این نیروهای پیشرانه برای غلبه بر جاذبه و کشیدن و هدایت وسیله نقلیه استفاده می شود.و در ضمن ببینید هر دو موتور موشک و جت از پیشرانه جت برای توسعه رانش استفاده می کنند. پیشرانه موشکی با هواپیمای جت متفاوت است که تنفس هوا هست زیرا موشک ها دارای پیشرانه های خودگردان هستند. اساس منبع انرژی طبقه بندی می شوند که برای تسریع سیال کار استفاده می شود. .
پیشرانه گاز سرد شامل یک منبع کنترل شده گاز تحت فشار و یک نازل ساده ترین شکل موتور موشک است.
تکانه ویژه به عنوان معیار سنجش عملکرد پیشرانه ها استفاده می شود. بر اساس قانون سوم نیوتن $\Large { { p _ 1 } } = { \left ( { m – d m } \right ) \left ( { v + d v } \right ) } $ومومنتوم گاز خارج شده $ \Large { p _ 2 } = d m \left ( { v – u } \right )$ قانون پایستگی مومنتوم و اینکه جرم موشک نسبت به زمان متغییر هست $ \Large { p = { p _ 1 } + { p _ 2 }\;\;}\Rightarrow { m v = \left( { m – d m } \right) \left( { v + d v } \right ) }+{ d m \left ( { v – u } \right)}$ به صورت $\Large m \frac { { d v } }{ { d t } } = u \frac { { d m } } {{ d t } } $که u برابر با سرعت گاز خروجی نسبت به موشک حالا شد حل معادله دیفرانسیل $\Large {dv = u\frac{{dm}}{m} \;\;}\Rightarrow { \int \limits _ { { v _ 0 } } ^ { {v _ 1 } } { d v } = \int \limits _ { { m _ 0 } } ^ { { m _ 1 } } { u \frac { { d m } } { m} } } $که بدست میاد $\Large \boxed {{{ v = u \ln \frac { { { m _ 0 } } } { m } } }} $ اگه من بگم جرم موشک با گذشت زمان به طور خطی تغییر میکند.$\Large m \left ( t \right ) = { m _ 0 } – \mu t $میشه بگم $ \Large { v \left ( t \right ) } = { u\ln \frac { { {m _0 } } }{ { { m _ 0 } – \mu t} } }$ حالا شتاب اون هم $\Large \require{cancel} {\frac{{dv}}{{dt}} = a\left( t \right) }
= {{u\frac{1}{{\frac{{{m_0}}}{{{m_0} – \mu t}}}} \cdot}\kern0pt { \frac { { \left( { – {m_0}} \right)\left( { – \mu } \right)}}{{{{\left( {{m_0} – \mu t} \right ) } ^ 2 } }} }} = { \frac { { u \mu } } { { { m _0 } – \mu t}}} $
توضیح نازل هایی که با کاهش سرعت جریان کار می کنند غلط و اشتباه انگیز هست . نازل ها همیشه جریان عبوری از آنها را تسریع می کنند. ابتدا باید درک کرد که چه نوع جریانی از نازل عبور می کند. . . اما .معادله کارایی یک راکت $ \eta_p= \frac {2\, (\frac {v} {v_e})} {1 + ( \frac {v} {v_e} )^2 }$که در آن v سرعت موشک است و ve سرعت خروجی است.
من هنوز عمیقاً متحیر هستم ، چگونه می تواند باشد که کارآیی موشک به سرعت بستگی دارد؟ همانطور که در مورد موشک ها می فهمم ، انتظار دارم همان مقدار سوخت بدون توجه به سرعت فعلی ، به همان افزایش سرعت تبدیل شود. .
پاسخ این است که سوخت در یک موشک در حال حرکت مقداری انرژی جنبشی دارد . بالاخره با سرعت زیادی نسبتاً به سمت زمین در حرکت است. مقدار این انرژی به سرعت حرکت موشک بستگی دارد و تا حدودی جای تعجب دارد که موتور موشک می تواند این انرژی را استخراج کرده و به کار مفید تبدیل کند. ممکن است مشاهده کنید که فرمولی که نشان داده اید درصورتی که سرعت موشک برابر با سرعت خروجی موشک (v = ve) باشد ، به بازدهی 100٪ می رسد. این بدان دلیل است که در صورت v = سرعت خروجی نسبتاً به زمین صفر خواهد بود و تمام انرژی جنبشی ذخیره شده در سوخت به طور کامل توسط موتور موشک استخراج می شود و برای تسریع موشک استفاده می شود.
در ارتفاع کم ، نازل موتور بیش از حد گسترش می یابد. فشار داخل لبه نازل کمتر از فشار محیط است ، بنابراین یک فشار فشاری روی نازل وجود دارد.
در ارتفاعات ، فشار محیط به جایی کاهش می یابد که از فشار داخل لبه نازل کمتر باشد: نازل در حال حاضر گسترش نیافته است و نیروی لبه به سمت خارج است.
تعریف جریان ایزنتروپیک این است که جریان هم آدیاباتیک است (هیچ گرمی به داخل یا خارج از آن منتقل نمی شود) و هم برگشت پذیر است (انرژی در آن صرفه جویی می شود). من تعجب می کنم که چرا جریان از طریق یک نازل موشک ایزنتروپیک است. آیا نباید انتقال گرما بین جریان و نازل و نیروی مقاومتی نازل را که هنگام عبور جریان تجربه می شود ، در نظر گرفت؟
علاوه بر این ، كتابی كه می خوانم می گوید كه سرعت جریان جرم ثابت است زیرا جریان ایزنتروپیك است ، كه كاملاً نمی فهمم: با عبور جریان از نازل ، منبسط و شتاب ، انرژی از فشار به سرعت می رسد. اما چگونه می توان از این نتیجه گرفت که سرعت جریان جرم ثابت است؟
نکته آخر اینکه مهم است که سرعت جریان جرم اگزوز هنگام عبور از نازل ثابت باشد. با این حال ، اگر ما در مورد توده اگزوز است که موشک را در یک واحد زمان ترک می کند ، آیا هنوز هم با تغییرات کمی بیشتر ثابت است؟ اگر چنین باشد ، آیا سرعت سرعت خروج اگزوز از موشک و رانش نیز با گذشت زمان ثابت است؟
جریان ایزنتروپیک
اول از همه: جریان در یک نازل موشک واقعی ایزنتروپیک نیست. این یک فرض ساده است که منطقی به مشاهدات اندازه گیری واقعی نزدیک هست خوب البته متغییر های زیادی هستند و من . همانطور که در مورد نظریه ایده آل موشک وجود دارد ، برسی میکنم
بنابراین کاملاً درست می گویید ، در اثر جاری شدن گرما به محیط اطراف و تلفات اصطکاک در دیواره نازل تلفاتی وجود دارد. با این حال ، اینها به اندازه کافی کوچک هستند که وانمود می کنند که در آنجا نیستند ، تقریب های خوبی در دنیای واقعی ارائه می دهد. صرفه نظر کردم دیدید
توجه داشته باشید که این تنها در صورتی است که جریان به تدریج گسترش یافته و فشرده شود. هنگامی که امواج شوک به دلیل انبساط بیش از حد یا کم در جریان وجود داشته باشند ، فرضیات ایزنتروپیک جریان دیگر کار نمی کند.
جریان انبوه ثابت
معادله ای که سپس به این جریان جرم می دهد:
$ \dot{m}=\frac{A_t p_c}{\sqrt{R\cdot T_c}} \sqrt{\gamma}\bigg(\frac{\gamma+1}{2}\bigg)^{-\frac{\gamma+1}{2(\gamma-1)}}$
با At ناحیه گلو ، pc فشار محفظه ، R ثابت گاز ، Tc دمای اتاق و γ نسبت گرمای خاص.
آنها را با عملکرد vandenkerckhove جایگزین کنیم
با At ناحیه گلو ، pc فشار محفظه ، R ثابت گاز ، Tc دمای محیط و γ نسبت گرمای خاص.
حالا، بنابراین اجازه دهید آنها را با عملکرد vandenkerckhove جایگزین کنیم Γ، فقط برای اینکه بهتر به نظر برسد
$ \dot{m}=\frac{\Gamma A_t p_c}{\sqrt{R\cdot T_c}}$
اکنون Γ و R ثابت هستند ، At باید ثابت باشد (مگر اینکه در اثر حرارت گلوی نازل شما ذوب شود: P) و pc و Tcباید ثابت باشد هنگامی که موتور شما در حالت ثابت کار می کند ، بنابراین جریان جرم شما ثابت خواهد بود. و معادله جریان جرمی داده شده . بنابراین به همین دلیل برای جریان ایزنتروپی جریان جرم ثابت است.
شرایط اگزوز
با حفظ ساده جرم ، هنگامی که جریان توده در گلو ثابت شد ، باید جریان در خروج نازل نیز جریان داشته باشد. در غیر این صورت توده بین حلق نازل و خروج جمع می شود. در زندگی واقعی مطمئناً نوساناتی وجود دارد و جریان جرم ممکن است توسط طراحی به دلیل فشار گاز تغییر کند ، اما تحت ایده آل نظریه موشک ثابت است.
با فرض اینکه فشار و دما محفظه ای که قبلاً گفتم ، تغییر نکرده اند ، سرعت معادل آن نیز ثابت است و بنابراین رانش می کند. از آنجا که رانش برابر است با جریان جرم برابر سرعت مشخصه $ F=\dot{m}\cdot v_{eq}$
* (تا زمانی که فشار محیط تغییر نکند ، بنابراین برای موشکی که به آرامی در جو بالا می رود سرعت برابر و رانش نیز تغییر می کند)
جریان جرم مستقیماً به وزن مولکولی از طریق ثابت گاز منفرد وابسته است که ثابت جهانی گاز بر وزن مولکولی آن تقسیم می شود
$R = \frac{R_u}{M_gas} $
غیرمستقیم: تغییر پیشران / احتراق برای بدست آوردن وزن مولکولی متفاوت ، همه پارامترهای دیگر را نیز تغییر می دهد به جز به احتمال زیاد.
بله و خیر. $ F=\dot{m}v_e$را اغلب مشاهده خواهید کرد ، اما این فقط در صورتی درست است که نازل به طور مطلوب منبسط شود ، بنابراین فشار خروجی برابر با فشار محیط است. بنابراین بهتر است از سرعت معادل داده شده توسط فرمول زیر استفاده کنید: $veq = ve + pe − pam˙⋅Ae$
با veq و ve به ترتیب و سرعت خروجی ، به ترتیب فشار خروج نازل ، فشار محیط ، متر مکعب سرعت جریان جرم و Ae منطقه خروج نازل همانطور که می بینید ve و veq برابر هستند اگر pe = pa ، اگر شتاب مداومی برای موشک خود داشته باشید ، این بدان معناست که شما باید دائماً گاز را پایین بکشید ، زیرا موشک شما با بیرون راندن همه پیشرانه سبک و سبک می شود. یا شاید شما بخواهید با سرعت کمتری از جو پایین عبور کنید تا کشش آنچنانی نداشته باشد بلکه از دست دادن نیروی جاذبه بیشتری داشته باشید. اما چگونگی و چرا گاز دادن بیشتر مربوط به موضوع Rocket Motion است که به خودی خوداندازه یک کتاب است. و بحث سنگینی هست من فقط مطلب ساده را میگم
بگویید موشک من می تواند F نیوتون رانش تولید کند در حالی که M1 کیلوگرم سوخت در ثانیه مصرف می کند. جرم آن در آغاز M0 است و تا زمانی که به سرعت V نرسد ، می سوزد.
چگونه می توانم زمان سوختن لازم برای رسیدن موشک به سرعت V را دریابم؟$\Delta T = \frac {M_L E_V} {F} (1 - e ^ {-\frac {\Delta V } {E_V}}) $ΔT: طول سوختگی در چند ثانیه
ML: جرم کل موشک در ابتدای سوختگی (که اغلب m0 نوشته می شود)
EV = سرعت اگزوز بر حسب متر / ثانیه (اغلب به صورت ve نوشته می شود).
F: رانش موشک در نیوتون.
ΔV = Delta-V سوختگی در متر بر ثانیه.
M0 شما این معادله ML است. سرعت اگزوز EV برابر با رانش تقسیم بر سرعت جریان جرم است (این F و M1 شما است).
سرعت اگزوز یکی از دو فرم استاندارد برای نشان دادن تکانه خاص جرم است. اما توجه کنید در محاسبات واقعی از نیروی ثانیه در هر پوند از جرم است استفاده میشود.
برای یک راکت من ، چگونه نیروی محرکه را محاسبه کنم
$F = \dot{m} V_e + (p_e - p_0) A_e $
محاسبه شتاب و فشار دینامیکی توجه کنید $q = \frac{1}{2} \rho v^2 $ و نیروی درگ $F_D = -\frac{1}{2} \rho C_D A v^2 $ خوی شتاب گرانشی هم $ a_{Grav} = -GM_E/(R_E+x)^2$حالا شتاب میدونید که $ a = \frac{F_{tot}}{m(t)} = \frac{F_{Thrust} + F_{Drag}}{m(t)} + a_{Grav}$
حالا در ضمن جرم متغییر داریم $m(t) = m_0 - \dot{m}t $
و نیروی تراست $F_{Thrust}=\dot{m} v_{ex} $بگذارید اینطور بگم $a = \frac{\dot{m} v_{ex} + F_{Drag}}{m_0 - \dot{m}t} + a_{Grav} $ که $a = \frac{\dot{m} v_{ex} - \frac{1}{2} \rho C_D A v^2}{m_0 - \dot{m}t} - \frac{GM_E}{(R_E+x)^2} $ نوشته میشه حالامن هنوز باید تراکم را برای تعریف q بدانم ، و ما می توانیم از یک تقریب ارتفاع مقیاس ساده استفاده کنیم که کمی شبیه نمودارهای فشار شما در برابر ارتفاع باشد. با فرض ثابت بودن دمای جو (که اینطور نیست) می توان گفت چگالی و فشار همیشه متناسب هستند. سپس$ \rho(x) = \rho_0 \exp(-x/h_{scale})$ خوب در معاددله بگذارم $ a(t) = \frac{\dot{m} v_{ex} - \frac{1}{2} \rho_0 \exp(-x(t)/h_{scale}) C_D A v^2(t)}{m_0 - \dot{m}t} - \frac{GM_E}{(R_E+x(t))^2}$این یک معادله است که هر سه این موارد را دارد: ارتفاع ، سرعت و شتاب (x ، v و a) و بنابراین حل کردن برای v (t) و x (t) برای بدست آوردن $q(t)=\frac{1}{2} \rho(t) v^2(t) = \frac{1}{2} \rho_0 \exp(-x(t)/h_{scale}) v^2(t) $
پیشرانه است که به وسیله آن نیرویی برای تغییر سرعت یک وسیله نقلیه اعمال می شود و هم سرعت آن و هم جهت آن را تحت تأثیر قرار می ده. رانش وارد شده به یک موشک به دلیل واکنش ناشی از حرکت یک جت پرسرعت است که در خلاف جهت شتاب گیری و البته.توجه کنید رانش متناسب با محصول دبی جریان جرم است ،، و سرعت ، V جت (یعنی) این نیروهای پیشرانه برای غلبه بر جاذبه و کشیدن و هدایت وسیله نقلیه استفاده می شود.و در ضمن ببینید هر دو موتور موشک و جت از پیشرانه جت برای توسعه رانش استفاده می کنند. پیشرانه موشکی با هواپیمای جت متفاوت است که تنفس هوا هست زیرا موشک ها دارای پیشرانه های خودگردان هستند. اساس منبع انرژی طبقه بندی می شوند که برای تسریع سیال کار استفاده می شود. .
پیشرانه گاز سرد شامل یک منبع کنترل شده گاز تحت فشار و یک نازل ساده ترین شکل موتور موشک است.
تکانه ویژه به عنوان معیار سنجش عملکرد پیشرانه ها استفاده می شود. بر اساس قانون سوم نیوتن $\Large { { p _ 1 } } = { \left ( { m – d m } \right ) \left ( { v + d v } \right ) } $ومومنتوم گاز خارج شده $ \Large { p _ 2 } = d m \left ( { v – u } \right )$ قانون پایستگی مومنتوم و اینکه جرم موشک نسبت به زمان متغییر هست $ \Large { p = { p _ 1 } + { p _ 2 }\;\;}\Rightarrow { m v = \left( { m – d m } \right) \left( { v + d v } \right ) }+{ d m \left ( { v – u } \right)}$ به صورت $\Large m \frac { { d v } }{ { d t } } = u \frac { { d m } } {{ d t } } $که u برابر با سرعت گاز خروجی نسبت به موشک حالا شد حل معادله دیفرانسیل $\Large {dv = u\frac{{dm}}{m} \;\;}\Rightarrow { \int \limits _ { { v _ 0 } } ^ { {v _ 1 } } { d v } = \int \limits _ { { m _ 0 } } ^ { { m _ 1 } } { u \frac { { d m } } { m} } } $که بدست میاد $\Large \boxed {{{ v = u \ln \frac { { { m _ 0 } } } { m } } }} $ اگه من بگم جرم موشک با گذشت زمان به طور خطی تغییر میکند.$\Large m \left ( t \right ) = { m _ 0 } – \mu t $میشه بگم $ \Large { v \left ( t \right ) } = { u\ln \frac { { {m _0 } } }{ { { m _ 0 } – \mu t} } }$ حالا شتاب اون هم $\Large \require{cancel} {\frac{{dv}}{{dt}} = a\left( t \right) }
= {{u\frac{1}{{\frac{{{m_0}}}{{{m_0} – \mu t}}}} \cdot}\kern0pt { \frac { { \left( { – {m_0}} \right)\left( { – \mu } \right)}}{{{{\left( {{m_0} – \mu t} \right ) } ^ 2 } }} }} = { \frac { { u \mu } } { { { m _0 } – \mu t}}} $
توضیح نازل هایی که با کاهش سرعت جریان کار می کنند غلط و اشتباه انگیز هست . نازل ها همیشه جریان عبوری از آنها را تسریع می کنند. ابتدا باید درک کرد که چه نوع جریانی از نازل عبور می کند. . . اما .معادله کارایی یک راکت $ \eta_p= \frac {2\, (\frac {v} {v_e})} {1 + ( \frac {v} {v_e} )^2 }$که در آن v سرعت موشک است و ve سرعت خروجی است.
من هنوز عمیقاً متحیر هستم ، چگونه می تواند باشد که کارآیی موشک به سرعت بستگی دارد؟ همانطور که در مورد موشک ها می فهمم ، انتظار دارم همان مقدار سوخت بدون توجه به سرعت فعلی ، به همان افزایش سرعت تبدیل شود. .
پاسخ این است که سوخت در یک موشک در حال حرکت مقداری انرژی جنبشی دارد . بالاخره با سرعت زیادی نسبتاً به سمت زمین در حرکت است. مقدار این انرژی به سرعت حرکت موشک بستگی دارد و تا حدودی جای تعجب دارد که موتور موشک می تواند این انرژی را استخراج کرده و به کار مفید تبدیل کند. ممکن است مشاهده کنید که فرمولی که نشان داده اید درصورتی که سرعت موشک برابر با سرعت خروجی موشک (v = ve) باشد ، به بازدهی 100٪ می رسد. این بدان دلیل است که در صورت v = سرعت خروجی نسبتاً به زمین صفر خواهد بود و تمام انرژی جنبشی ذخیره شده در سوخت به طور کامل توسط موتور موشک استخراج می شود و برای تسریع موشک استفاده می شود.
در ارتفاع کم ، نازل موتور بیش از حد گسترش می یابد. فشار داخل لبه نازل کمتر از فشار محیط است ، بنابراین یک فشار فشاری روی نازل وجود دارد.
در ارتفاعات ، فشار محیط به جایی کاهش می یابد که از فشار داخل لبه نازل کمتر باشد: نازل در حال حاضر گسترش نیافته است و نیروی لبه به سمت خارج است.
تعریف جریان ایزنتروپیک این است که جریان هم آدیاباتیک است (هیچ گرمی به داخل یا خارج از آن منتقل نمی شود) و هم برگشت پذیر است (انرژی در آن صرفه جویی می شود). من تعجب می کنم که چرا جریان از طریق یک نازل موشک ایزنتروپیک است. آیا نباید انتقال گرما بین جریان و نازل و نیروی مقاومتی نازل را که هنگام عبور جریان تجربه می شود ، در نظر گرفت؟
علاوه بر این ، كتابی كه می خوانم می گوید كه سرعت جریان جرم ثابت است زیرا جریان ایزنتروپیك است ، كه كاملاً نمی فهمم: با عبور جریان از نازل ، منبسط و شتاب ، انرژی از فشار به سرعت می رسد. اما چگونه می توان از این نتیجه گرفت که سرعت جریان جرم ثابت است؟
نکته آخر اینکه مهم است که سرعت جریان جرم اگزوز هنگام عبور از نازل ثابت باشد. با این حال ، اگر ما در مورد توده اگزوز است که موشک را در یک واحد زمان ترک می کند ، آیا هنوز هم با تغییرات کمی بیشتر ثابت است؟ اگر چنین باشد ، آیا سرعت سرعت خروج اگزوز از موشک و رانش نیز با گذشت زمان ثابت است؟
جریان ایزنتروپیک
اول از همه: جریان در یک نازل موشک واقعی ایزنتروپیک نیست. این یک فرض ساده است که منطقی به مشاهدات اندازه گیری واقعی نزدیک هست خوب البته متغییر های زیادی هستند و من . همانطور که در مورد نظریه ایده آل موشک وجود دارد ، برسی میکنم
بنابراین کاملاً درست می گویید ، در اثر جاری شدن گرما به محیط اطراف و تلفات اصطکاک در دیواره نازل تلفاتی وجود دارد. با این حال ، اینها به اندازه کافی کوچک هستند که وانمود می کنند که در آنجا نیستند ، تقریب های خوبی در دنیای واقعی ارائه می دهد. صرفه نظر کردم دیدید
توجه داشته باشید که این تنها در صورتی است که جریان به تدریج گسترش یافته و فشرده شود. هنگامی که امواج شوک به دلیل انبساط بیش از حد یا کم در جریان وجود داشته باشند ، فرضیات ایزنتروپیک جریان دیگر کار نمی کند.
جریان انبوه ثابت
معادله ای که سپس به این جریان جرم می دهد:
$ \dot{m}=\frac{A_t p_c}{\sqrt{R\cdot T_c}} \sqrt{\gamma}\bigg(\frac{\gamma+1}{2}\bigg)^{-\frac{\gamma+1}{2(\gamma-1)}}$
با At ناحیه گلو ، pc فشار محفظه ، R ثابت گاز ، Tc دمای اتاق و γ نسبت گرمای خاص.
آنها را با عملکرد vandenkerckhove جایگزین کنیم
با At ناحیه گلو ، pc فشار محفظه ، R ثابت گاز ، Tc دمای محیط و γ نسبت گرمای خاص.
حالا، بنابراین اجازه دهید آنها را با عملکرد vandenkerckhove جایگزین کنیم Γ، فقط برای اینکه بهتر به نظر برسد
$ \dot{m}=\frac{\Gamma A_t p_c}{\sqrt{R\cdot T_c}}$
اکنون Γ و R ثابت هستند ، At باید ثابت باشد (مگر اینکه در اثر حرارت گلوی نازل شما ذوب شود: P) و pc و Tcباید ثابت باشد هنگامی که موتور شما در حالت ثابت کار می کند ، بنابراین جریان جرم شما ثابت خواهد بود. و معادله جریان جرمی داده شده . بنابراین به همین دلیل برای جریان ایزنتروپی جریان جرم ثابت است.
شرایط اگزوز
با حفظ ساده جرم ، هنگامی که جریان توده در گلو ثابت شد ، باید جریان در خروج نازل نیز جریان داشته باشد. در غیر این صورت توده بین حلق نازل و خروج جمع می شود. در زندگی واقعی مطمئناً نوساناتی وجود دارد و جریان جرم ممکن است توسط طراحی به دلیل فشار گاز تغییر کند ، اما تحت ایده آل نظریه موشک ثابت است.
با فرض اینکه فشار و دما محفظه ای که قبلاً گفتم ، تغییر نکرده اند ، سرعت معادل آن نیز ثابت است و بنابراین رانش می کند. از آنجا که رانش برابر است با جریان جرم برابر سرعت مشخصه $ F=\dot{m}\cdot v_{eq}$
* (تا زمانی که فشار محیط تغییر نکند ، بنابراین برای موشکی که به آرامی در جو بالا می رود سرعت برابر و رانش نیز تغییر می کند)
جریان جرم مستقیماً به وزن مولکولی از طریق ثابت گاز منفرد وابسته است که ثابت جهانی گاز بر وزن مولکولی آن تقسیم می شود
$R = \frac{R_u}{M_gas} $
غیرمستقیم: تغییر پیشران / احتراق برای بدست آوردن وزن مولکولی متفاوت ، همه پارامترهای دیگر را نیز تغییر می دهد به جز به احتمال زیاد.
بله و خیر. $ F=\dot{m}v_e$را اغلب مشاهده خواهید کرد ، اما این فقط در صورتی درست است که نازل به طور مطلوب منبسط شود ، بنابراین فشار خروجی برابر با فشار محیط است. بنابراین بهتر است از سرعت معادل داده شده توسط فرمول زیر استفاده کنید: $veq = ve + pe − pam˙⋅Ae$
با veq و ve به ترتیب و سرعت خروجی ، به ترتیب فشار خروج نازل ، فشار محیط ، متر مکعب سرعت جریان جرم و Ae منطقه خروج نازل همانطور که می بینید ve و veq برابر هستند اگر pe = pa ، اگر شتاب مداومی برای موشک خود داشته باشید ، این بدان معناست که شما باید دائماً گاز را پایین بکشید ، زیرا موشک شما با بیرون راندن همه پیشرانه سبک و سبک می شود. یا شاید شما بخواهید با سرعت کمتری از جو پایین عبور کنید تا کشش آنچنانی نداشته باشد بلکه از دست دادن نیروی جاذبه بیشتری داشته باشید. اما چگونگی و چرا گاز دادن بیشتر مربوط به موضوع Rocket Motion است که به خودی خوداندازه یک کتاب است. و بحث سنگینی هست من فقط مطلب ساده را میگم
بگویید موشک من می تواند F نیوتون رانش تولید کند در حالی که M1 کیلوگرم سوخت در ثانیه مصرف می کند. جرم آن در آغاز M0 است و تا زمانی که به سرعت V نرسد ، می سوزد.
چگونه می توانم زمان سوختن لازم برای رسیدن موشک به سرعت V را دریابم؟$\Delta T = \frac {M_L E_V} {F} (1 - e ^ {-\frac {\Delta V } {E_V}}) $ΔT: طول سوختگی در چند ثانیه
ML: جرم کل موشک در ابتدای سوختگی (که اغلب m0 نوشته می شود)
EV = سرعت اگزوز بر حسب متر / ثانیه (اغلب به صورت ve نوشته می شود).
F: رانش موشک در نیوتون.
ΔV = Delta-V سوختگی در متر بر ثانیه.
M0 شما این معادله ML است. سرعت اگزوز EV برابر با رانش تقسیم بر سرعت جریان جرم است (این F و M1 شما است).
سرعت اگزوز یکی از دو فرم استاندارد برای نشان دادن تکانه خاص جرم است. اما توجه کنید در محاسبات واقعی از نیروی ثانیه در هر پوند از جرم است استفاده میشود.
برای یک راکت من ، چگونه نیروی محرکه را محاسبه کنم
$F = \dot{m} V_e + (p_e - p_0) A_e $
محاسبه شتاب و فشار دینامیکی توجه کنید $q = \frac{1}{2} \rho v^2 $ و نیروی درگ $F_D = -\frac{1}{2} \rho C_D A v^2 $ خوی شتاب گرانشی هم $ a_{Grav} = -GM_E/(R_E+x)^2$حالا شتاب میدونید که $ a = \frac{F_{tot}}{m(t)} = \frac{F_{Thrust} + F_{Drag}}{m(t)} + a_{Grav}$
حالا در ضمن جرم متغییر داریم $m(t) = m_0 - \dot{m}t $
و نیروی تراست $F_{Thrust}=\dot{m} v_{ex} $بگذارید اینطور بگم $a = \frac{\dot{m} v_{ex} + F_{Drag}}{m_0 - \dot{m}t} + a_{Grav} $ که $a = \frac{\dot{m} v_{ex} - \frac{1}{2} \rho C_D A v^2}{m_0 - \dot{m}t} - \frac{GM_E}{(R_E+x)^2} $ نوشته میشه حالامن هنوز باید تراکم را برای تعریف q بدانم ، و ما می توانیم از یک تقریب ارتفاع مقیاس ساده استفاده کنیم که کمی شبیه نمودارهای فشار شما در برابر ارتفاع باشد. با فرض ثابت بودن دمای جو (که اینطور نیست) می توان گفت چگالی و فشار همیشه متناسب هستند. سپس$ \rho(x) = \rho_0 \exp(-x/h_{scale})$ خوب در معاددله بگذارم $ a(t) = \frac{\dot{m} v_{ex} - \frac{1}{2} \rho_0 \exp(-x(t)/h_{scale}) C_D A v^2(t)}{m_0 - \dot{m}t} - \frac{GM_E}{(R_E+x(t))^2}$این یک معادله است که هر سه این موارد را دارد: ارتفاع ، سرعت و شتاب (x ، v و a) و بنابراین حل کردن برای v (t) و x (t) برای بدست آوردن $q(t)=\frac{1}{2} \rho(t) v^2(t) = \frac{1}{2} \rho_0 \exp(-x(t)/h_{scale}) v^2(t) $

- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: هوافضا
خوب ابتدا با اصول دینامیک پرواز و سازه ها و محاسبات ایرودینامیک و ایرفویل ها اشنا بشین بعد ساخت اون واقعیت: گلایدر دارای مخازن بالاست است که می تواند با آب پر شود. اضافه شدن بالاست باعث افزایش وزن می شود و این باعث می شود که هواپیمای گلایدر در سرعت هوایی سریعتر پرواز کند و در همان حالت نسبت سر خوردن را حفظ کند. این بدان معناست که اگر دو گلایدر P1 و P2 هر دو از یک مدل باشند ، در نقطه A شروع می شوند و وزن P2 بیشتر از P1 است ، هر دو در نقطه B پایان می یابند ، اما P2 قبل از P1 می رسد. حرکت بصورت خطی است و در طول پرواز ، هر هواپیما می تواند سرعت هوای ثابت و عمودی را حفظ کند ، سرعت P2 بیشتر از P1 است. زاویه حمله نیز ممکن است متفاوت باشد.:برای ساده کردن موارد ، بیایید در نظر بگیریم که حرکت در داخل هوای یکنواخت انجام می شود ، بدون تغییر چگالی با ارتفاع ، و باد آرام است. من برخی از کتاب های راهنمای هواپیمایی را خوانده ام و بیشترین توضیحات ارائه شده در مورد این است که گلایدر همان نسبت Lift / Drag (L / D) را حفظ می کند ،. من با مهارت های بسیار محدود خود سعی در رسیدن به عبارتی دارم که مربوط به سرعت با وزن باشد ، اما تقریباً همیشه در این روند دچار اشتباه میشم
. از آنجایی که گلایدرها (معمولاً) موتور ندارند ، رانش دیگری وجود ندارد و تنها نیروهای موجود Lift (L) ، Drag (D) و Weight (W) هستند. همانطور که حرکت یکنواخت است ، شتاب صفر است. سپس ، قانون دوم نیوتن به ما می گوید:${\vec F = m·\vec a} $از آنجا که جرم نمی تواند تهی باشد ، بنابراین نیروی حاصل از آن باید صفر باشد. بنابراین ما:$ {\vec F = \vec F_x + \vec F_y}$و${\vec F_x = \vec L_x + \vec D_x = \vec 0} $و${\vec F_y = \vec L_y + \vec D_y + \vec W_y= \vec 0} $لیفت ${L = \frac{C_L(\alpha)V^2 \rho S}{2} } $در حالی که$ {C_L(\alpha)}$ ضریب بالابر است که متناسب با زاویه حمله زیر اصطبل است.V سرعت است. ρ تراکم هوا استS سطح بال است.فرمول کشیدن عبارت است از:${D = C_D(\alpha) q S } $ و$ {C_D(\alpha)}$ ضریب درگ است که تابعی از زاویه حمله است ، تقریباً درجه دوم است.q فشار دینامیکی است در اینجا تلاش من برای بیان سرعت به عنوان تابعی از جرم است:${\vec F_y = \vec L_y + \vec D_y + \vec W_y= \vec 0} $
و${|\vec L|\cos(\varphi) = -|\vec D|\sin(\varphi) -gm} $و${\frac{C_L(\alpha)V^2 \rho S}{2}\cos(\varphi) = -C_D(\alpha) q S \sin(\varphi) -gm} $
از آنجا که ضرایب بالابر و کشیدن برای یک زاویه مشخص از حمله ثابت هستند ، ρ و q ثابت هستند زیرا هوا یکنواخت است و S ثابت است زیرا گلایدر بدون تغییر ناحیه بال پرواز می کند (بدون افزودن فلپ) ، می توانیم ثابت ها را گروه بندی کنیم و این چیزی است که ما بدست می آوریم:${k V^2 = -g m + k'} $ همانطور که نشان داده شده ، AB بال هواپیمای گلایدر است. پیکان زرد جهت سرعت V گلایدر است. G وزن گلایدر است. G دو components دارد ، یکی component $G_t $ موازی جهت سرعت و دیگری component $ G_n$ عمود بر جهت سرعت است. همچنین دو جز components نیروی هوایی اعمال شده به بال وجود دارد ، یکی جز component D به موازات جهت سرعت و دیگری جز L عمود بر جهت سرعت است.
اگر سرعت V گلایدر کم باشد ، $G_t $> D و$G_n> L $ است. بنابراین ، تحت رانش$G_t $ ، سرعت V گلایدر افزایش می یابد. با افزایش سرعت V ، D افزایش می یابد و L افزایش می یابد. سرانجام ، $G_t $ = D ، L = $G_n $ ، و گلایدر با سرعت یکنواخت در امتداد خط زرد سر می خورد.اگر آن را کنار بگذاریم و فرض کنیم سرعت v ثابت است ، من می توانم کشش را ببینم ، $ D = Av^{-2}$ میزان اتلاف انرژی است (با یک کوچک در مقابل به طوری که $v \approx \frac {dx} {dt} $ در جایی که x قرار دارد) زیرا$ Power, P = \frac{d} {dt} \int{D dx} = \frac{d} {dt} \int{Av^{-2} dx} = Av^{-2} \frac {dx} {dt} \approx Av^{-1}$ تقریب $ \Rightarrow mgv_s \approx Av^{-1} \Rightarrow v_s \approx \frac {Av^{-1}} {mg}$ توان تولید شده توسط وزن جسم
از این تحلیل گلایدر ، می توان دریافت که پرواز گلایدر یک پرواز رانش است. بدون نیروی جاذبه به عنوان رانش ، گلایدر نمی تواند پرواز کند و نمی تواند بالابر تولید کند.
با افزایش وزن G گلگیر ، $ G_t$ بزرگتری بدست می آید ، بنابراین گلایدر می تواند بیشتر پرواز کندنیروهایی که روی گلایدر عمل می کنند
، برای غلبه بر کشیدن ، به برخی از اجزای افقی بالابر نیاز دارید. و کشش شما بیش از فقط جز مولفه القا شده است - تلفات اصطکاک از همان اندازه هستند.
توجه داشته باشید که من بردارها را طوری جابجا کردم که بتوان نشان داد مثلث نیرو بسته است و نیروها در تعادل هستند. v∞ سرعت هوا نسبت به گلایدر است که در اثر حرکت گلایدر ایجاد می شود. شیب لازم است تا بردار بالابر (که در هر تعریف نسبت به بردار سرعت هوا متعامد است) به سمت جلو متمایل شود ، در نتیجه یک مولفه افقی برابر با کشش است.$\frac{dE_{pot}}{dt} = m\cdot g \cdot\frac{dh}{dt} \approx W\cdot v $با تعادل نیروها (L = بلند کردن ، D = کشیدن)$L = -m\cdot g\cdot cos\gamma \;\text{and}\; D = -L\cdot tan\gamma $و$ m\cdot g \cdot\frac{dh}{dt} = m\cdot g \cdot cos\gamma\cdot v\cdot tan\gamma \;\text{and}\; tan\gamma = -\frac{D}{L} = -\frac{c_D}{c_L}$و$v_z = -v\cdot sin\gamma = v\cdot\frac{c_D}{\sqrt{c_L^2+c_D^2}} \approx v\cdot\frac{c_D}{c_L} $و$c_D = c_{D0}+\frac{c_L^2}{\pi\cdot AR\cdot\epsilon} $و$v_z \approx v\cdot\left(\frac{c_{D0}}{c_L}+\frac{c_L}{\pi\cdot AR \cdot \epsilon} \right) $که من g شتاب گرانشی
v سرعت پرواز
ضریب $c_{D}\;\;\;\; $
$c_{D0}\;\;\; $ ضریب درگ آسانسور
ضریب $c_{L}\;\;\;\; $
$\gamma\;\;\;\;\;\; $ زاویه مسیر پرواز ، هنگام اشاره به سمت بالا از حالت افقی ، مثبت است
π3.14159
نسبت ابعاد بال (مساحت مربع در مساحت$AR$
$\epsilon\;\;\;\;\;\;\, $ ، به طور معمول بین 0.7 تا 1. برای گلایدرها 0.98 معمولی است
به هر حال ، در یک سرعت معین ، کشش D ناشی از آن فقط کسری از نیروی بالابرنده است ، بنابراین کسری مشخص از میلی گرم است. اکثر گلایدرهای خوب نسبت سر خوردن در حدود 30: 1 دارند ، بنابراین کشیدن باید در حدود mg / 30 باشد ، و این شامل انگلی و همچنین ناشی از آن است.،
. از آنجایی که گلایدرها (معمولاً) موتور ندارند ، رانش دیگری وجود ندارد و تنها نیروهای موجود Lift (L) ، Drag (D) و Weight (W) هستند. همانطور که حرکت یکنواخت است ، شتاب صفر است. سپس ، قانون دوم نیوتن به ما می گوید:${\vec F = m·\vec a} $از آنجا که جرم نمی تواند تهی باشد ، بنابراین نیروی حاصل از آن باید صفر باشد. بنابراین ما:$ {\vec F = \vec F_x + \vec F_y}$و${\vec F_x = \vec L_x + \vec D_x = \vec 0} $و${\vec F_y = \vec L_y + \vec D_y + \vec W_y= \vec 0} $لیفت ${L = \frac{C_L(\alpha)V^2 \rho S}{2} } $در حالی که$ {C_L(\alpha)}$ ضریب بالابر است که متناسب با زاویه حمله زیر اصطبل است.V سرعت است. ρ تراکم هوا استS سطح بال است.فرمول کشیدن عبارت است از:${D = C_D(\alpha) q S } $ و$ {C_D(\alpha)}$ ضریب درگ است که تابعی از زاویه حمله است ، تقریباً درجه دوم است.q فشار دینامیکی است در اینجا تلاش من برای بیان سرعت به عنوان تابعی از جرم است:${\vec F_y = \vec L_y + \vec D_y + \vec W_y= \vec 0} $
و${|\vec L|\cos(\varphi) = -|\vec D|\sin(\varphi) -gm} $و${\frac{C_L(\alpha)V^2 \rho S}{2}\cos(\varphi) = -C_D(\alpha) q S \sin(\varphi) -gm} $
از آنجا که ضرایب بالابر و کشیدن برای یک زاویه مشخص از حمله ثابت هستند ، ρ و q ثابت هستند زیرا هوا یکنواخت است و S ثابت است زیرا گلایدر بدون تغییر ناحیه بال پرواز می کند (بدون افزودن فلپ) ، می توانیم ثابت ها را گروه بندی کنیم و این چیزی است که ما بدست می آوریم:${k V^2 = -g m + k'} $ همانطور که نشان داده شده ، AB بال هواپیمای گلایدر است. پیکان زرد جهت سرعت V گلایدر است. G وزن گلایدر است. G دو components دارد ، یکی component $G_t $ موازی جهت سرعت و دیگری component $ G_n$ عمود بر جهت سرعت است. همچنین دو جز components نیروی هوایی اعمال شده به بال وجود دارد ، یکی جز component D به موازات جهت سرعت و دیگری جز L عمود بر جهت سرعت است.
اگر سرعت V گلایدر کم باشد ، $G_t $> D و$G_n> L $ است. بنابراین ، تحت رانش$G_t $ ، سرعت V گلایدر افزایش می یابد. با افزایش سرعت V ، D افزایش می یابد و L افزایش می یابد. سرانجام ، $G_t $ = D ، L = $G_n $ ، و گلایدر با سرعت یکنواخت در امتداد خط زرد سر می خورد.اگر آن را کنار بگذاریم و فرض کنیم سرعت v ثابت است ، من می توانم کشش را ببینم ، $ D = Av^{-2}$ میزان اتلاف انرژی است (با یک کوچک در مقابل به طوری که $v \approx \frac {dx} {dt} $ در جایی که x قرار دارد) زیرا$ Power, P = \frac{d} {dt} \int{D dx} = \frac{d} {dt} \int{Av^{-2} dx} = Av^{-2} \frac {dx} {dt} \approx Av^{-1}$ تقریب $ \Rightarrow mgv_s \approx Av^{-1} \Rightarrow v_s \approx \frac {Av^{-1}} {mg}$ توان تولید شده توسط وزن جسم
از این تحلیل گلایدر ، می توان دریافت که پرواز گلایدر یک پرواز رانش است. بدون نیروی جاذبه به عنوان رانش ، گلایدر نمی تواند پرواز کند و نمی تواند بالابر تولید کند.
با افزایش وزن G گلگیر ، $ G_t$ بزرگتری بدست می آید ، بنابراین گلایدر می تواند بیشتر پرواز کندنیروهایی که روی گلایدر عمل می کنند
، برای غلبه بر کشیدن ، به برخی از اجزای افقی بالابر نیاز دارید. و کشش شما بیش از فقط جز مولفه القا شده است - تلفات اصطکاک از همان اندازه هستند.
توجه داشته باشید که من بردارها را طوری جابجا کردم که بتوان نشان داد مثلث نیرو بسته است و نیروها در تعادل هستند. v∞ سرعت هوا نسبت به گلایدر است که در اثر حرکت گلایدر ایجاد می شود. شیب لازم است تا بردار بالابر (که در هر تعریف نسبت به بردار سرعت هوا متعامد است) به سمت جلو متمایل شود ، در نتیجه یک مولفه افقی برابر با کشش است.$\frac{dE_{pot}}{dt} = m\cdot g \cdot\frac{dh}{dt} \approx W\cdot v $با تعادل نیروها (L = بلند کردن ، D = کشیدن)$L = -m\cdot g\cdot cos\gamma \;\text{and}\; D = -L\cdot tan\gamma $و$ m\cdot g \cdot\frac{dh}{dt} = m\cdot g \cdot cos\gamma\cdot v\cdot tan\gamma \;\text{and}\; tan\gamma = -\frac{D}{L} = -\frac{c_D}{c_L}$و$v_z = -v\cdot sin\gamma = v\cdot\frac{c_D}{\sqrt{c_L^2+c_D^2}} \approx v\cdot\frac{c_D}{c_L} $و$c_D = c_{D0}+\frac{c_L^2}{\pi\cdot AR\cdot\epsilon} $و$v_z \approx v\cdot\left(\frac{c_{D0}}{c_L}+\frac{c_L}{\pi\cdot AR \cdot \epsilon} \right) $که من g شتاب گرانشی
v سرعت پرواز
ضریب $c_{D}\;\;\;\; $
$c_{D0}\;\;\; $ ضریب درگ آسانسور
ضریب $c_{L}\;\;\;\; $
$\gamma\;\;\;\;\;\; $ زاویه مسیر پرواز ، هنگام اشاره به سمت بالا از حالت افقی ، مثبت است
π3.14159
نسبت ابعاد بال (مساحت مربع در مساحت$AR$
$\epsilon\;\;\;\;\;\;\, $ ، به طور معمول بین 0.7 تا 1. برای گلایدرها 0.98 معمولی است
به هر حال ، در یک سرعت معین ، کشش D ناشی از آن فقط کسری از نیروی بالابرنده است ، بنابراین کسری مشخص از میلی گرم است. اکثر گلایدرهای خوب نسبت سر خوردن در حدود 30: 1 دارند ، بنابراین کشیدن باید در حدود mg / 30 باشد ، و این شامل انگلی و همچنین ناشی از آن است.،

- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: هوافضا
آیا موتور جت برقی امکان پذیر است؟
شما نمی توانید یک هواپیمای جت برقی داشته باشید. یک هواپیمای جت دارای یک موتور توربین است و کل اصل موتور توربین شامل یک محفظه احتراق است که به این معنی است که از سوخت جت برای ایجاد احتراق استفاده می شود.موتور جت برقی چگونه کار می کند؟
تیغه ها با سرعت زیاد می چرخند و هوا را فشرده یا فشرده می کنند. سپس هوای فشرده با سوخت پاشیده می شود و یک جرقه الکتریکی مخلوط را روشن می کند. گازهای سوزاننده منبسط می شوند و از طریق نازل، در پشت موتور، منفجر می شوند. همانطور که جت های گاز به سمت عقب شلیک می کنند، موتور و هواپیما به جلو رانده می شوند.آیا موتور جت می تواند برقی باشد؟
من علاقه مند به درک چگونگی تولید برق در موتورهای جت هستم. اگر یک خلبان به طور مداوم دریچه گاز را مطابق با نیازهای پرواز تغییر دهد، موتور جت چگونه گشتاور ثابتی را برای ژنراتورها حفظ می کند، با توجه به اینکه بار روی ژنراتورها نسبتاً پایدار است؟ من به سه راه حل خوب فکر کردم
مجموعه ای از چرخ دنده ها را در امتداد شفت اصلی برای کنترل دیفرانسیل گشتاور نصب کنید.
خروجی چند محفظه احتراق به یک توربین کوچک جداگانه متصل به یک ژنراتور. این ترتیب به کنترل کننده اجازه می دهد تا به طور مستقل سوخت را در این محفظه های احتراق کنترل کند و اطمینان حاصل کند که خروجی برای تغذیه ژنراتورها بهینه است.از هوای خروجی موتورها استفاده کنید و مقداری توربین بادی را به حرکت درآورید. من این گزینه را بسیار بعید می دانم.همه جت ها و توربوفن ها گیربکسی را اجرا می کنند که از شفت قرقره بیرونی خارج می شود. گیربکس دارای لنت های محرک برای تمام لوازم جانبی برق مانند پمپ های هیدرولیک، پمپ های سوخت و ژنراتور و یک پد محرک ورودی برای استارت است. موتور با هر سرعتی که میخواهد بهصورتی که خلبان تعیین کرده است کار میکند، و نیازهای خدماتی که از گیربکس خارج میشود فقط به باری که باید با آن بپردازد میافزاید. در پایان، اگر بار الکتریکی بالا برود، فقط به این معنی است که کنترل کننده سوخت باید سوخت بیشتری را در مشعل بریزد تا سرعتی را که به آن گفته می شود حفظ کند.
ژنراتورها در اکثر جت های مدرن معمولاً جریان متناوب 3 فاز 110 ولتی با فرکانس ثابت 400 هرتز دارند. آنها از یک درایو دنده ورودی متغیر استفاده می کنند که ژنراتور را در دور در دقیقه نگه می دارد که یک فرکانس خروجی ثابت 400 هرتز را بدون توجه به سرعت ورودی موتور، که مورد نیاز تمام لوازم الکترونیکی است، می دهد. به اینها مولد درایوهای مجتمع می گویند.
همچنین ممکن است ژنراتورهای AC فرکانس متغیر را مشاهده کنید که با هر سرعتی که موتور با آن کار می کند و فرکانس متناوب با سرعت تغییر می کند، کار می کنند. شما نمی توانید از فرکانس متناوب AC برای سیستم های اویونیک استفاده کنید، بنابراین این نوع ژنراتورها ممکن است فقط چیزهایی مانند بخاری ها و سایر خدمات حساس به فرکانس را تغذیه کنند، و فرکانس AC ثابت توسط اینورترهای ساکن که برق DC را قطع می کنند، ارائه می شود که توسط یک DC جداگانه ارائه می شود.در واقع حداقل از سه روش مختلف استفاده می شود (من می گویم چون من 3 مورد را می شناسم و می تواند بیشتر باشد). بنابراین گفتن "همه هواپیماها" کاملاً درست نیست. اجازه دهید با آنچه به نظر من مهمترین معادله است، قانون فارادی (ساده شده) شروع کنیم:
$\mathcal{E}=-N\frac{\mathrm{d}{BAcos{\omega t}}}{\mathrm{d}t}\$
این به ما می گوید که راه های مختلفی برای تولید یک خروجی EMF (E) وجود دارد. دو مورد مربوط به این بحث B و ω هستند. توجه داشته باشید ω فرکانس زاویه ای است که می توان آن را به RPM تغییر داد.
هواپیماهای GA، از جمله جتهای بیز، احتمالاً از ژنراتور DC یا دینام DC استفاده خواهند کرد. در یک سیستم DC، با توجه به اینکه این هواپیماهای سبک کوچک هستند، ما در واقع B را در قانون فارادی کنترل می کنیم. یعنی اگر RPM افزایش یابد، آنگاه قدرت میدان مغناطیسی داخل ژنراتور را کاهش می دهیم. این منجر به یک خروجی متعادل می شود. واحد کنترل ژنراتور (GCU) وظیفه انجام این کار را بر عهده دارد. به طور موثر، به طور مداوم خروجی ژنراتور (یا دینام DC) را اندازه گیری می کند و با کاهش ولتاژ خروجی، جریان ارائه شده به سیم پیچ های میدان (کویل ها یا سیم هایی که میدان مغناطیسی را تولید می کنند، که یک آهنربای الکتریکی است) افزایش می یابد. به طور مشابه، اگر خروجی زیاد شود، جریان به سیم پیچ های میدان کاهش می یابد. مدار در زیر نشان داده شده است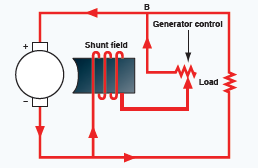
تنظیم ولتاژ ژنراتور توسط رئوستات میدانی
برای هواپیماهای دسته حمل و نقل بزرگ، دو گزینه وجود دارد. اینها سیستم های قدیمی و راه حل مدرن تر هواپیماهای برقی هستند که در B787 و A350 استفاده می شوند (و مطمئن هستم در انواع مدرن بدنه هواپیماهای قدیمی تر). همانطور که قبلا ذکر شد، برای هواپیماهای رده حمل و نقل بزرگ قدیمی، بخشی از قانون فارادی که کنترل می شود RPM است. این را نمی توان در داخل دینام AC انجام داد، بنابراین باید قبل از آن انجام شود. همانطور که گفته شد، واحد درایو سرعت ثابت (CDU) با دینام AC ترکیب می شود تا یک ژنراتور درایو یکپارچه (IDG) ایجاد کند. CDU یک سیستم انتقال هیدرواستاتیک است. در این حالت چرخش ورودی یک سیال هیدرولیکی را پمپاژ می کند که بسته به RPM ورودی فشار آن افزایش و کاهش می یابد. GCU اکنون یک صفحه تلوتلو را در سیستم های انتقال به کار می اندازد که از ثابت بودن فشار سیال هیدرولیک خروجی اطمینان می دهد. این سیال فشار ثابت سپس به "توربین" خروجی یا درایو هیدرولیک داده می شود که خروجی را با سرعت ثابتی می چرخاند. این یک RPM ثابت برای دینام می دهد. یک شکل در زیر نشان داده شده است، اگرچه فوق العاده مفید نیست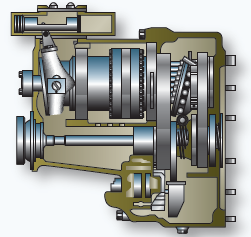
یک درایو با سرعت ثابت هیدرولیک برای دینام AC
برای هواپیماهای حمل و نقل بزرگ مدرن، هیچ یک از موارد فوق اتفاق نمی افتد. اینها سیستمهای ACFW نامیده میشوند، یعنی سیستمهای وحشی با فرکانس AC (جریان جایگزین). در اینجا، اجازه می دهیم ژنراتور استارت (که هنوز دارای GCU است، بنابراین یک باند عملیاتی وجود دارد که باید حفظ شود) چرخش با تغییر RPM موتور تغییر کند. این فرکانس های متناوب AC بسیار متفاوتی را در زمان های مختلف تولید می کند (دور در دقیقه موتور). سپس بلافاصله به DC تبدیل می شود. برای استفاده از این امر در سیستم هایی که نیاز به جریان متناوب دارند، معمولاً از سیگنال 3 فاز 115 ولت/120 ولت 400 هرتز استفاده می شود، سپس از اینورترهای استاتیک برای تبدیل سیگنال DC به سیگنال AC مورد نیاز استفاده می شود. در اینها، ما به طور موثر یک سیگنال DC را روشن و خاموش می کنیم، آن را به یک ترانسفورماتور (و سایر مدارهای تهویه مطبوع) می دهیم تا سیگنال AC مورد نیاز را ایجاد کند. به عنوان مثال، از همین نوع سیستم قدرت در F-22 و F-35 استفاده می شود.
موتور جت الکتریکی چیست؟ موتور جت برقی از همان اصل موتور توربوجت پیروی می کند، با این تفاوت که به جای چرخاندن توربین دوم برای افزودن نیرو به کمپرسور، از نیروی الکتریکی استفاده می کند.چرخش این تیغهها همچنین یک شفت مرکزی را میچرخاند که - جدا از اینکه بخش مرکزی در کارکردن موتور است - میتواند برای چرخاندن یک ژنراتور الکتریکی نیز استفاده شود. در 787 Dreamliner، دو استارت/ژنراتور موتور فرکانس متغیر در هر موتور وجود داردآیا موتور جت می تواند برق تولید کند؟
هر موتور حداقل یک ژنراتور بزرگ دارد، واحد برق کمکی یک ژنراتور دارد و اکثر جت های خطوط هوایی دارای یک توربین هوای رم هستند که می تواند برق تولید کند. باتری هم هست ژنراتورهای موتور باعث می شوند موتور سوخت بیشتری بسوزاند، اما این مقدار زیاد نیست.ژنراتورها در هواپیماهای جت بیشتر رایج هستند. ژنراتورها را می توان به عنوان شروع کننده نیز استفاده کرد. از نیروی باتری برای چرخاندن ژنراتور استفاده می شود که موتور را برای راه اندازی به بالا می چرخاند. هنگامی که موتور روشن می شود، موتور ژنراتور را می چرخاند تا برق تولید کند.
APU ها
هواپیماهای مسافربری و هواپیماهای توربین بزرگ به نیروی زیادی نیاز دارند. همچنین، قدرت باتری به تنهایی برای چرخاندن یک موتور جت بزرگ برای راه اندازی آن کافی نیست.
APU واحد برق کمکی هانیول
واحد برق کمکی (APU)
برای رفع این مشکلات، جت ها معمولاً به یک واحد قدرت کمکی (APU) مجهز می شوند. اینها موتورهای توربین کوچکی هستند که در قسمت دم نصب شده اند که ژنراتورهای برق را راه اندازی می کنند و هوای خونی ایجاد می کنند. اینها برای راه اندازی به انرژی بسیار کمتری نیاز دارند، بنابراین می توان آنها را با باتری راه اندازی کرد.
اما آنها به اندازهای بزرگ هستند که میتوانند برق تولید کنند تا در هواپیما استفاده شود و آن باتریها را شارژ کنند. آنها همچنین درست مانند موتورهای اصلی هوای خونی ایجاد می کنند که می تواند به راه اندازی موتورهای اصلی کمک کند. آنها همچنین از هوای خونی خود برای سیستم های محیطی استفاده می کنند.
پردازنده های گرافیکی
واحدهای برق زمینی (GPU) روی آسفالت برای کمک به پرواز هواپیماها در صورت تمام شدن باتریهایشان استفاده میشوند. در برخی موارد، آنها مانند کابل های جامپر برای هواپیما استفاده می شوند.
DmitryPilots میتواند هنگام تنظیم تجهیزات الکترونیکی کابین خلبان قبل از پرواز از قدرت GPU استفاده کند
اما از آنها برای تامین برق هواپیما بدون روشن کردن موتورها نیز استفاده می شود. راه اندازی موتورها گران است و سوخت را می سوزاند. اگر هواپیما برای مدتی نشسته باشد، می توان از پردازنده گرافیکی برای تامین برق ارزان قیمت استفاده کرد. اگر خلبانها تجهیزات ناوبری را برنامهریزی میکنند یا مسافران به تهویه مطبوع یا گرمایش روشن نیاز دارند، عالی است.
پردازندههای گرافیکی معمولاً «کارتهای زمینی» نامیده میشوند.
تدابیر ضروری
مهم ترین چیزی که باید به خاطر داشته باشید این است که اکثر هواپیماها به گونه ای طراحی شده اند که یک خرابی مشکل مهمی نخواهد بود. در هواپیماهایی که تنها یک دینام دارند، هیچ تجهیزات حیاتی برای پرواز نباید از کار بیفتد.
برخلاف خودروها که از دینام و باتری برای تولید جرقه موتور استفاده می کنند، هواپیماها از آهنرباهای جداگانه برای انجام این کار استفاده می کنند. در اکثر خودروها، اگر دینام از کار بیفتد، موتور پس از تخلیه باتری از بین می رود. اما خلبانان حتی می توانند برق خود را در حین پرواز بدون خطر توقف موتور خاموش کنند. موتور برای کار کردن نیازی به برق ندارد.
مصرف کنندگان متصل به سیستم الکتریکی یا برای پرواز حیاتی نیستند (مانند فلپ ها و لوازم الکترونیکی)، یا دارای باتری پشتیبان هستند.
بسیاری از هواپیماهای جدید دارای موتورهای کنترل شده توسط کامپیوتر به نام FADEC (کنترل موتور دیجیتال با اختیار کامل) هستند. این سیستم ها از رایانه های الکتریکی اضافی برای کنترل پارامترهای موتور استفاده می کنند. از آنجایی که خرابی سیستم الکتریکی به معنای خرابی موتور است، این کامپیوترها باتری های مخصوص به خود را دارند.
سیستم الکتریکی یکی از بخشهای هواپیما است که خلبانان باید به خوبی در آن مهارت داشته باشند. اگر توانایی تولید برق خود را از دست بدهند، پس از خالی شدن باتریها چه چیزی خراب میشود؟ چه مدت می توانند با خیال راحت روی باتری به تنهایی بمانند؟ اگر هواپیما دارای موتورهای FADEC باشد، موتورها تا چه مدت با باتری های پشتیبان خود کار می کنند؟
شما نمی توانید یک هواپیمای جت برقی داشته باشید. یک هواپیمای جت دارای یک موتور توربین است و کل اصل موتور توربین شامل یک محفظه احتراق است که به این معنی است که از سوخت جت برای ایجاد احتراق استفاده می شود.موتور جت برقی چگونه کار می کند؟
تیغه ها با سرعت زیاد می چرخند و هوا را فشرده یا فشرده می کنند. سپس هوای فشرده با سوخت پاشیده می شود و یک جرقه الکتریکی مخلوط را روشن می کند. گازهای سوزاننده منبسط می شوند و از طریق نازل، در پشت موتور، منفجر می شوند. همانطور که جت های گاز به سمت عقب شلیک می کنند، موتور و هواپیما به جلو رانده می شوند.آیا موتور جت می تواند برقی باشد؟
من علاقه مند به درک چگونگی تولید برق در موتورهای جت هستم. اگر یک خلبان به طور مداوم دریچه گاز را مطابق با نیازهای پرواز تغییر دهد، موتور جت چگونه گشتاور ثابتی را برای ژنراتورها حفظ می کند، با توجه به اینکه بار روی ژنراتورها نسبتاً پایدار است؟ من به سه راه حل خوب فکر کردم
مجموعه ای از چرخ دنده ها را در امتداد شفت اصلی برای کنترل دیفرانسیل گشتاور نصب کنید.
خروجی چند محفظه احتراق به یک توربین کوچک جداگانه متصل به یک ژنراتور. این ترتیب به کنترل کننده اجازه می دهد تا به طور مستقل سوخت را در این محفظه های احتراق کنترل کند و اطمینان حاصل کند که خروجی برای تغذیه ژنراتورها بهینه است.از هوای خروجی موتورها استفاده کنید و مقداری توربین بادی را به حرکت درآورید. من این گزینه را بسیار بعید می دانم.همه جت ها و توربوفن ها گیربکسی را اجرا می کنند که از شفت قرقره بیرونی خارج می شود. گیربکس دارای لنت های محرک برای تمام لوازم جانبی برق مانند پمپ های هیدرولیک، پمپ های سوخت و ژنراتور و یک پد محرک ورودی برای استارت است. موتور با هر سرعتی که میخواهد بهصورتی که خلبان تعیین کرده است کار میکند، و نیازهای خدماتی که از گیربکس خارج میشود فقط به باری که باید با آن بپردازد میافزاید. در پایان، اگر بار الکتریکی بالا برود، فقط به این معنی است که کنترل کننده سوخت باید سوخت بیشتری را در مشعل بریزد تا سرعتی را که به آن گفته می شود حفظ کند.
ژنراتورها در اکثر جت های مدرن معمولاً جریان متناوب 3 فاز 110 ولتی با فرکانس ثابت 400 هرتز دارند. آنها از یک درایو دنده ورودی متغیر استفاده می کنند که ژنراتور را در دور در دقیقه نگه می دارد که یک فرکانس خروجی ثابت 400 هرتز را بدون توجه به سرعت ورودی موتور، که مورد نیاز تمام لوازم الکترونیکی است، می دهد. به اینها مولد درایوهای مجتمع می گویند.
همچنین ممکن است ژنراتورهای AC فرکانس متغیر را مشاهده کنید که با هر سرعتی که موتور با آن کار می کند و فرکانس متناوب با سرعت تغییر می کند، کار می کنند. شما نمی توانید از فرکانس متناوب AC برای سیستم های اویونیک استفاده کنید، بنابراین این نوع ژنراتورها ممکن است فقط چیزهایی مانند بخاری ها و سایر خدمات حساس به فرکانس را تغذیه کنند، و فرکانس AC ثابت توسط اینورترهای ساکن که برق DC را قطع می کنند، ارائه می شود که توسط یک DC جداگانه ارائه می شود.در واقع حداقل از سه روش مختلف استفاده می شود (من می گویم چون من 3 مورد را می شناسم و می تواند بیشتر باشد). بنابراین گفتن "همه هواپیماها" کاملاً درست نیست. اجازه دهید با آنچه به نظر من مهمترین معادله است، قانون فارادی (ساده شده) شروع کنیم:
$\mathcal{E}=-N\frac{\mathrm{d}{BAcos{\omega t}}}{\mathrm{d}t}\$
این به ما می گوید که راه های مختلفی برای تولید یک خروجی EMF (E) وجود دارد. دو مورد مربوط به این بحث B و ω هستند. توجه داشته باشید ω فرکانس زاویه ای است که می توان آن را به RPM تغییر داد.
هواپیماهای GA، از جمله جتهای بیز، احتمالاً از ژنراتور DC یا دینام DC استفاده خواهند کرد. در یک سیستم DC، با توجه به اینکه این هواپیماهای سبک کوچک هستند، ما در واقع B را در قانون فارادی کنترل می کنیم. یعنی اگر RPM افزایش یابد، آنگاه قدرت میدان مغناطیسی داخل ژنراتور را کاهش می دهیم. این منجر به یک خروجی متعادل می شود. واحد کنترل ژنراتور (GCU) وظیفه انجام این کار را بر عهده دارد. به طور موثر، به طور مداوم خروجی ژنراتور (یا دینام DC) را اندازه گیری می کند و با کاهش ولتاژ خروجی، جریان ارائه شده به سیم پیچ های میدان (کویل ها یا سیم هایی که میدان مغناطیسی را تولید می کنند، که یک آهنربای الکتریکی است) افزایش می یابد. به طور مشابه، اگر خروجی زیاد شود، جریان به سیم پیچ های میدان کاهش می یابد. مدار در زیر نشان داده شده است

تنظیم ولتاژ ژنراتور توسط رئوستات میدانی
برای هواپیماهای دسته حمل و نقل بزرگ، دو گزینه وجود دارد. اینها سیستم های قدیمی و راه حل مدرن تر هواپیماهای برقی هستند که در B787 و A350 استفاده می شوند (و مطمئن هستم در انواع مدرن بدنه هواپیماهای قدیمی تر). همانطور که قبلا ذکر شد، برای هواپیماهای رده حمل و نقل بزرگ قدیمی، بخشی از قانون فارادی که کنترل می شود RPM است. این را نمی توان در داخل دینام AC انجام داد، بنابراین باید قبل از آن انجام شود. همانطور که گفته شد، واحد درایو سرعت ثابت (CDU) با دینام AC ترکیب می شود تا یک ژنراتور درایو یکپارچه (IDG) ایجاد کند. CDU یک سیستم انتقال هیدرواستاتیک است. در این حالت چرخش ورودی یک سیال هیدرولیکی را پمپاژ می کند که بسته به RPM ورودی فشار آن افزایش و کاهش می یابد. GCU اکنون یک صفحه تلوتلو را در سیستم های انتقال به کار می اندازد که از ثابت بودن فشار سیال هیدرولیک خروجی اطمینان می دهد. این سیال فشار ثابت سپس به "توربین" خروجی یا درایو هیدرولیک داده می شود که خروجی را با سرعت ثابتی می چرخاند. این یک RPM ثابت برای دینام می دهد. یک شکل در زیر نشان داده شده است، اگرچه فوق العاده مفید نیست

یک درایو با سرعت ثابت هیدرولیک برای دینام AC
برای هواپیماهای حمل و نقل بزرگ مدرن، هیچ یک از موارد فوق اتفاق نمی افتد. اینها سیستمهای ACFW نامیده میشوند، یعنی سیستمهای وحشی با فرکانس AC (جریان جایگزین). در اینجا، اجازه می دهیم ژنراتور استارت (که هنوز دارای GCU است، بنابراین یک باند عملیاتی وجود دارد که باید حفظ شود) چرخش با تغییر RPM موتور تغییر کند. این فرکانس های متناوب AC بسیار متفاوتی را در زمان های مختلف تولید می کند (دور در دقیقه موتور). سپس بلافاصله به DC تبدیل می شود. برای استفاده از این امر در سیستم هایی که نیاز به جریان متناوب دارند، معمولاً از سیگنال 3 فاز 115 ولت/120 ولت 400 هرتز استفاده می شود، سپس از اینورترهای استاتیک برای تبدیل سیگنال DC به سیگنال AC مورد نیاز استفاده می شود. در اینها، ما به طور موثر یک سیگنال DC را روشن و خاموش می کنیم، آن را به یک ترانسفورماتور (و سایر مدارهای تهویه مطبوع) می دهیم تا سیگنال AC مورد نیاز را ایجاد کند. به عنوان مثال، از همین نوع سیستم قدرت در F-22 و F-35 استفاده می شود.
موتور جت الکتریکی چیست؟ موتور جت برقی از همان اصل موتور توربوجت پیروی می کند، با این تفاوت که به جای چرخاندن توربین دوم برای افزودن نیرو به کمپرسور، از نیروی الکتریکی استفاده می کند.چرخش این تیغهها همچنین یک شفت مرکزی را میچرخاند که - جدا از اینکه بخش مرکزی در کارکردن موتور است - میتواند برای چرخاندن یک ژنراتور الکتریکی نیز استفاده شود. در 787 Dreamliner، دو استارت/ژنراتور موتور فرکانس متغیر در هر موتور وجود داردآیا موتور جت می تواند برق تولید کند؟
هر موتور حداقل یک ژنراتور بزرگ دارد، واحد برق کمکی یک ژنراتور دارد و اکثر جت های خطوط هوایی دارای یک توربین هوای رم هستند که می تواند برق تولید کند. باتری هم هست ژنراتورهای موتور باعث می شوند موتور سوخت بیشتری بسوزاند، اما این مقدار زیاد نیست.ژنراتورها در هواپیماهای جت بیشتر رایج هستند. ژنراتورها را می توان به عنوان شروع کننده نیز استفاده کرد. از نیروی باتری برای چرخاندن ژنراتور استفاده می شود که موتور را برای راه اندازی به بالا می چرخاند. هنگامی که موتور روشن می شود، موتور ژنراتور را می چرخاند تا برق تولید کند.
APU ها
هواپیماهای مسافربری و هواپیماهای توربین بزرگ به نیروی زیادی نیاز دارند. همچنین، قدرت باتری به تنهایی برای چرخاندن یک موتور جت بزرگ برای راه اندازی آن کافی نیست.
APU واحد برق کمکی هانیول
واحد برق کمکی (APU)
برای رفع این مشکلات، جت ها معمولاً به یک واحد قدرت کمکی (APU) مجهز می شوند. اینها موتورهای توربین کوچکی هستند که در قسمت دم نصب شده اند که ژنراتورهای برق را راه اندازی می کنند و هوای خونی ایجاد می کنند. اینها برای راه اندازی به انرژی بسیار کمتری نیاز دارند، بنابراین می توان آنها را با باتری راه اندازی کرد.
اما آنها به اندازهای بزرگ هستند که میتوانند برق تولید کنند تا در هواپیما استفاده شود و آن باتریها را شارژ کنند. آنها همچنین درست مانند موتورهای اصلی هوای خونی ایجاد می کنند که می تواند به راه اندازی موتورهای اصلی کمک کند. آنها همچنین از هوای خونی خود برای سیستم های محیطی استفاده می کنند.
پردازنده های گرافیکی
واحدهای برق زمینی (GPU) روی آسفالت برای کمک به پرواز هواپیماها در صورت تمام شدن باتریهایشان استفاده میشوند. در برخی موارد، آنها مانند کابل های جامپر برای هواپیما استفاده می شوند.
DmitryPilots میتواند هنگام تنظیم تجهیزات الکترونیکی کابین خلبان قبل از پرواز از قدرت GPU استفاده کند
اما از آنها برای تامین برق هواپیما بدون روشن کردن موتورها نیز استفاده می شود. راه اندازی موتورها گران است و سوخت را می سوزاند. اگر هواپیما برای مدتی نشسته باشد، می توان از پردازنده گرافیکی برای تامین برق ارزان قیمت استفاده کرد. اگر خلبانها تجهیزات ناوبری را برنامهریزی میکنند یا مسافران به تهویه مطبوع یا گرمایش روشن نیاز دارند، عالی است.
پردازندههای گرافیکی معمولاً «کارتهای زمینی» نامیده میشوند.
تدابیر ضروری
مهم ترین چیزی که باید به خاطر داشته باشید این است که اکثر هواپیماها به گونه ای طراحی شده اند که یک خرابی مشکل مهمی نخواهد بود. در هواپیماهایی که تنها یک دینام دارند، هیچ تجهیزات حیاتی برای پرواز نباید از کار بیفتد.
برخلاف خودروها که از دینام و باتری برای تولید جرقه موتور استفاده می کنند، هواپیماها از آهنرباهای جداگانه برای انجام این کار استفاده می کنند. در اکثر خودروها، اگر دینام از کار بیفتد، موتور پس از تخلیه باتری از بین می رود. اما خلبانان حتی می توانند برق خود را در حین پرواز بدون خطر توقف موتور خاموش کنند. موتور برای کار کردن نیازی به برق ندارد.
مصرف کنندگان متصل به سیستم الکتریکی یا برای پرواز حیاتی نیستند (مانند فلپ ها و لوازم الکترونیکی)، یا دارای باتری پشتیبان هستند.
بسیاری از هواپیماهای جدید دارای موتورهای کنترل شده توسط کامپیوتر به نام FADEC (کنترل موتور دیجیتال با اختیار کامل) هستند. این سیستم ها از رایانه های الکتریکی اضافی برای کنترل پارامترهای موتور استفاده می کنند. از آنجایی که خرابی سیستم الکتریکی به معنای خرابی موتور است، این کامپیوترها باتری های مخصوص به خود را دارند.
سیستم الکتریکی یکی از بخشهای هواپیما است که خلبانان باید به خوبی در آن مهارت داشته باشند. اگر توانایی تولید برق خود را از دست بدهند، پس از خالی شدن باتریها چه چیزی خراب میشود؟ چه مدت می توانند با خیال راحت روی باتری به تنهایی بمانند؟ اگر هواپیما دارای موتورهای FADEC باشد، موتورها تا چه مدت با باتری های پشتیبان خود کار می کنند؟

- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: هوافضا
roham ، برای یک چرخه کامل از یک موتور گرما ،$e \leqslant 1 - \frac{T_c}{T_h}, $و $\frac{Q_c}{T_c} - \frac{Q_h}{T_h} = \Delta S \geqslant 0. $که این کل تغییر در آنتروپی است زیرا وی هیچ آنتروپی ایجاد شده به دلیل کار توسط موتور را به حساب نمی آورد. من فرض می کنم مشکلی با استدلال من اشتباه است ، اما چه؟
: به عنوان مثال ، یک موتور حرارتی را در نظر بگیرید که یک توپ را بلند می کند و آن را رها می کند و در نتیجه انرژی داخلی را افزایش می دهد و بنابراین آنتروپی کف زمین که توپ روی آن قرار می گیرد افزایش می یابد. گرما از مخزن گرم و به مخزن سرد می رود.
* نمی دانم چرا نباید جمله ای را با حرف اضافه تمام کنم2
اگر Th دمای مخزن گرم است و Tc دمای مخزن سرد است ، پس معادله صحیح برای تعادل آنتروپی روی مایع در حال کار است
$ \Delta S=\frac{Q_h}{T_h}-\frac{Q_c}{T_c}+S_{\text{gen}}$
جایی که $ S_{\text{gen}}$ آنتروپی برگشت ناپذیر تولید شده در طول چرخه است. اما ، از آنجا که موتور در یک چرخه کار می کند و آنتروپی تابعی از حالت است ، ΔS = 0. بنابراین،
$ \frac{Q_h}{T_h}-\frac{Q_c}{T_c}+S_{\text{gen}}=0\tag{1}$
همچنین ، از آنجا که$S_{\text{gen}} $ همیشه بزرگتر یا برابر با صفر است ، این نتایج نیز با نابرابری Clausius مطابقت دارند ، که برای این وضعیت ، به موارد زیر تبدیل می شود:
$\Delta S=0\gt\frac{Q_h}{T_h}-\frac{Q_c}{T_c} $
از آنجا که $ W=Q_h-Q_c$ ، از Eqn پیروی می کند. 1 که:
$\frac{Q_h}{T_h}-\frac{Q_h-W}{T_c}+S_{\text{gen}}=0 $یا معادل آن ،
$\eta=\frac{W}{Q_h}=\left(1-\frac{T_c}{T_h}\right)-\frac{S_{\text{gen}}T_c}{Q_h}\lt \left(1-\frac{T_c}{T_h}\right) $
بنابراین بازدهی کمتر از موتور برگشت پذیر کارنو است.
این معادله تغییر کل آنتروپی (سیستم + محیط اطراف) است و احتمال ایجاد آنتروپی در موتور را به حساب می آورد.
تغییر آنتروپی سیستم برای هر چرخه کامل همیشه صفر است (برگشت پذیر یا غیر قابل برگشت) زیرا آنتروپی عملکرد تابعی سیستم است و به مسیر بستگی ندارد. در نتیجه ، هر آنتروپی ایجاد شده توسط سیستم به محیط اطراف منتقل می شود. اگر یک موتور گرمایی آنتروپی ایجاد کند ، چرخه برگشت پذیر نیست ، و
$ \Delta S_{tot}>0$از طرف دیگر ، اگر یک موتور گرمایی بین دو مخزن حرارتی در یک چرخه برگشت پذیر کار کند (چرخه کارنو) موتور گرما آنتروپی ایجاد نمی کند و$\Delta S_{tot}=0 $
بهره وری-برای هر موتور حرارتی که بین دو مخزن حرارتی کار می کند ، بازده چرخه کار خالص انجام شده بر گرمای ناخالص اضافه شده است ، یا$e=\frac {Q_{h}-Q_{c}}{Q_h} $
اگر چرخه برگشت پذیر باشد (چرخه کارنو)$ \Delta S_{tot}=\frac{Q_c}{T_c}-\frac{Q_h}{T_h}=0$
و بنابراین$ e=1-\frac{T_c}{T_h}$که کارایی کارنو است.اگر چرخه غیرقابل برگشت باشد ،$ \Delta S_{tot}=\frac{Q_c}{T_c}-\frac{Q_h}{T_h}>0$و $ \frac {Q_c}{T_c}>\frac {Q_h}{T_h}$و $\frac {Q_c}{Q_h}>\frac {T_c}{T_h} $و $ e=1-\frac{Q_c}{Q_h}<1-\frac{T_c}{T_h}$
هر آنتروپی ایجاد شده در سیستم (به دلیل کار برگشت ناپذیر یا در غیر این صورت) در یک چرخه برای صفر تغییر در آنتروپی سیستم نیاز به انتقال به اطراف دارد. برای انتقال آنتروپی بین سیستم و محیط اطراف دو روش وجود دارد. جریان گرما و جرم. جریان انبوه به دلیل آنتروپی خاصیت ماده است بنابراین اگر ماده از سیستم خارج شود ، آنتروپی خود را با خود می برد. برای یک سیستم بسته (به عنوان سیستمی تعریف شده است که انتقال جرم را مجاز نمی داند) که فقط گرما باقی می گذارد.
بنابراین برای مثال ما ، هر آنتروپی تولید شده در سیستم میزان گرمای رد شده را افزایش می دهد و کارایی چرخه را کاهش می دهد.
یک نمونه کلاسیک از یک فرآیند برگشت ناپذیر که شامل انتقال گرما نیست ، انبساط آدیاباتیک آزاد یک گاز ایده آل است.
یک محفظه عایق صلب به دو قسمت مساوی تقسیم می شود. نیمی از محفظه حاوی گاز ایده آل است. نیمه دیگر خلا است. روزنه ای در پارتیشن ایجاد می شود که به گاز اجازه می دهد آزادانه به نیمه تخلیه گسترش یابد. از آنجا که محفظه عایق بندی شده است ، هیچ انتقال حرارتی وجود ندارد (0 = Q). از آنجا که انبساط گاز مرزهای محفظه را گسترش نمی دهد ، هیچ کار مرزی وجود ندارد (0 = W). در نتیجه ، طبق قانون اول ، تغییر در انرژی داخلی صفر است (ΔU = 0). به عنوان یک گاز ایده آل ، جایی که تغییر در انرژی داخلی فقط به تغییر دما بستگی دارد ، بنابراین تغییری در دما ایجاد نمی شود.
نتیجه نهایی این است که حجم دو برابر شده و فشار به نصف کاهش یافته و دما تغییر نکرده است.
اگرچه هیچ انتقال حرارتی رخ نداده است ، اما پروسه بدیهی است که برگشت پذیر نیست (انتظار ندارید که گاز به طور خود به خود به نیمه اصلی محفظه برگردد). اما ما می توانیم با انجام هر فرآیند برگشت پذیر مناسب برای بازگرداندن گاز به شرایط اولیه ، آنتروپی تولید شده را تعیین کنیم. انتخاب واضح در اینجا حذف عایق و انجام فشرده سازی همدما برگشت پذیر است. برای انجام این کار نیاز به انتقال گرما به محیط اطراف است. این مقدار گرما نشان دهنده "کار از دست رفته" است ، یعنی کاری که می توانست انجام شود اگر انبساط آزاد گاز با انبساط آدیاباتیک برگشت پذیر جایگزین شود.
مثال بعدی توجه کنید
ما یک سیلندر عایق بندی شده داریم که دارای یک گاز ایده آل با یک پیستون وزنه نشسته در بالا است ، به طوری که فشار اولیه روی گاز P1 = 10atm است. به منحنی 1 در زیر مراجعه کنید. ما به طور ناگهانی وزن را از بین می بریم تا فشار خارجی نصف شود ، یا P2a = 5atm. این امر منجر به انبساط آدیاباتیک غیر شبه ایستا (غیر قابل برگشت) در برابر فشار خارجی ثابت می شود. با استفاده از قوانین ایده آل گاز ، می توان حجم و دمای نهایی (نقطه 2a) را هنگام رسیدن به تعادل تعیین کرد ، با این فرض که حجم و دمای اولیه همانطور که برای نقطه 1 نشان داده شده است. کار انجام شده صرفاً فشار خارجی چند برابر تغییر حجم است.
ما می توانیم فرآیند برگشت ناپذیر را با انبساط آدیاباتیک برگشت پذیر مقایسه کنیم که در آن فشار نهایی همان فشار نهایی انبساط برگشت ناپذیر باشد. منحنی 2 را در زیر مشاهده کنید. آنچه خواهیم فهمید ، حجم نهایی و دمای نهایی انبساط آدیاباتیک برگشت پذیر (نقطه 2 منحنی) کمتر از انبساط برگشت ناپذیر است و کار انجام شده (منطقه زیر نمودار P-V) بیشتر از انبساط برگشت ناپذیر است.
حال می خواهیم سیستمی را که تحت انبساط برگشت ناپذیر (منحنی 1) قرار داشته است ، به حالت اولیه خود برگردانیم تا یک چرخه کامل به ما ارائه دهد. برای این کار می توان یک فشرده سازی ایزوباریک (فشار ثابت) گاز را از نقطه 2a به نقطه 2 انجام داد تا حجم و دمای آن کاهش یابد تا با حجم نهایی در انتهای انبساط برگشت پذیر مطابقت داشته باشد. این ما را به منحنی آدیاباتیک برگشت پذیر بازمی گرداند. اما همچنین نیاز به انتقال گرما از گاز به محیط اطراف دارد. بار دیگر ، این انتقال گرما معادل "کار از دست رفته" فرآیند برگشت ناپذیر خواهد بود. ما با انجام یک فشرده سازی آدیاباتیک برگشت پذیر از نقطه 2 به 1 فرآیند را کامل می کنیم تا سیستم را به حالت اولیه برگردانیم.
برای هر دو مورد نتیجه نهایی تولید آنتروپی انتقال گرما به محیط اطراف است
: به عنوان مثال ، یک موتور حرارتی را در نظر بگیرید که یک توپ را بلند می کند و آن را رها می کند و در نتیجه انرژی داخلی را افزایش می دهد و بنابراین آنتروپی کف زمین که توپ روی آن قرار می گیرد افزایش می یابد. گرما از مخزن گرم و به مخزن سرد می رود.
* نمی دانم چرا نباید جمله ای را با حرف اضافه تمام کنم2
اگر Th دمای مخزن گرم است و Tc دمای مخزن سرد است ، پس معادله صحیح برای تعادل آنتروپی روی مایع در حال کار است
$ \Delta S=\frac{Q_h}{T_h}-\frac{Q_c}{T_c}+S_{\text{gen}}$
جایی که $ S_{\text{gen}}$ آنتروپی برگشت ناپذیر تولید شده در طول چرخه است. اما ، از آنجا که موتور در یک چرخه کار می کند و آنتروپی تابعی از حالت است ، ΔS = 0. بنابراین،
$ \frac{Q_h}{T_h}-\frac{Q_c}{T_c}+S_{\text{gen}}=0\tag{1}$
همچنین ، از آنجا که$S_{\text{gen}} $ همیشه بزرگتر یا برابر با صفر است ، این نتایج نیز با نابرابری Clausius مطابقت دارند ، که برای این وضعیت ، به موارد زیر تبدیل می شود:
$\Delta S=0\gt\frac{Q_h}{T_h}-\frac{Q_c}{T_c} $
از آنجا که $ W=Q_h-Q_c$ ، از Eqn پیروی می کند. 1 که:
$\frac{Q_h}{T_h}-\frac{Q_h-W}{T_c}+S_{\text{gen}}=0 $یا معادل آن ،
$\eta=\frac{W}{Q_h}=\left(1-\frac{T_c}{T_h}\right)-\frac{S_{\text{gen}}T_c}{Q_h}\lt \left(1-\frac{T_c}{T_h}\right) $
بنابراین بازدهی کمتر از موتور برگشت پذیر کارنو است.
این معادله تغییر کل آنتروپی (سیستم + محیط اطراف) است و احتمال ایجاد آنتروپی در موتور را به حساب می آورد.
تغییر آنتروپی سیستم برای هر چرخه کامل همیشه صفر است (برگشت پذیر یا غیر قابل برگشت) زیرا آنتروپی عملکرد تابعی سیستم است و به مسیر بستگی ندارد. در نتیجه ، هر آنتروپی ایجاد شده توسط سیستم به محیط اطراف منتقل می شود. اگر یک موتور گرمایی آنتروپی ایجاد کند ، چرخه برگشت پذیر نیست ، و
$ \Delta S_{tot}>0$از طرف دیگر ، اگر یک موتور گرمایی بین دو مخزن حرارتی در یک چرخه برگشت پذیر کار کند (چرخه کارنو) موتور گرما آنتروپی ایجاد نمی کند و$\Delta S_{tot}=0 $
بهره وری-برای هر موتور حرارتی که بین دو مخزن حرارتی کار می کند ، بازده چرخه کار خالص انجام شده بر گرمای ناخالص اضافه شده است ، یا$e=\frac {Q_{h}-Q_{c}}{Q_h} $
اگر چرخه برگشت پذیر باشد (چرخه کارنو)$ \Delta S_{tot}=\frac{Q_c}{T_c}-\frac{Q_h}{T_h}=0$
و بنابراین$ e=1-\frac{T_c}{T_h}$که کارایی کارنو است.اگر چرخه غیرقابل برگشت باشد ،$ \Delta S_{tot}=\frac{Q_c}{T_c}-\frac{Q_h}{T_h}>0$و $ \frac {Q_c}{T_c}>\frac {Q_h}{T_h}$و $\frac {Q_c}{Q_h}>\frac {T_c}{T_h} $و $ e=1-\frac{Q_c}{Q_h}<1-\frac{T_c}{T_h}$
هر آنتروپی ایجاد شده در سیستم (به دلیل کار برگشت ناپذیر یا در غیر این صورت) در یک چرخه برای صفر تغییر در آنتروپی سیستم نیاز به انتقال به اطراف دارد. برای انتقال آنتروپی بین سیستم و محیط اطراف دو روش وجود دارد. جریان گرما و جرم. جریان انبوه به دلیل آنتروپی خاصیت ماده است بنابراین اگر ماده از سیستم خارج شود ، آنتروپی خود را با خود می برد. برای یک سیستم بسته (به عنوان سیستمی تعریف شده است که انتقال جرم را مجاز نمی داند) که فقط گرما باقی می گذارد.
بنابراین برای مثال ما ، هر آنتروپی تولید شده در سیستم میزان گرمای رد شده را افزایش می دهد و کارایی چرخه را کاهش می دهد.
یک نمونه کلاسیک از یک فرآیند برگشت ناپذیر که شامل انتقال گرما نیست ، انبساط آدیاباتیک آزاد یک گاز ایده آل است.
یک محفظه عایق صلب به دو قسمت مساوی تقسیم می شود. نیمی از محفظه حاوی گاز ایده آل است. نیمه دیگر خلا است. روزنه ای در پارتیشن ایجاد می شود که به گاز اجازه می دهد آزادانه به نیمه تخلیه گسترش یابد. از آنجا که محفظه عایق بندی شده است ، هیچ انتقال حرارتی وجود ندارد (0 = Q). از آنجا که انبساط گاز مرزهای محفظه را گسترش نمی دهد ، هیچ کار مرزی وجود ندارد (0 = W). در نتیجه ، طبق قانون اول ، تغییر در انرژی داخلی صفر است (ΔU = 0). به عنوان یک گاز ایده آل ، جایی که تغییر در انرژی داخلی فقط به تغییر دما بستگی دارد ، بنابراین تغییری در دما ایجاد نمی شود.
نتیجه نهایی این است که حجم دو برابر شده و فشار به نصف کاهش یافته و دما تغییر نکرده است.
اگرچه هیچ انتقال حرارتی رخ نداده است ، اما پروسه بدیهی است که برگشت پذیر نیست (انتظار ندارید که گاز به طور خود به خود به نیمه اصلی محفظه برگردد). اما ما می توانیم با انجام هر فرآیند برگشت پذیر مناسب برای بازگرداندن گاز به شرایط اولیه ، آنتروپی تولید شده را تعیین کنیم. انتخاب واضح در اینجا حذف عایق و انجام فشرده سازی همدما برگشت پذیر است. برای انجام این کار نیاز به انتقال گرما به محیط اطراف است. این مقدار گرما نشان دهنده "کار از دست رفته" است ، یعنی کاری که می توانست انجام شود اگر انبساط آزاد گاز با انبساط آدیاباتیک برگشت پذیر جایگزین شود.
مثال بعدی توجه کنید
ما یک سیلندر عایق بندی شده داریم که دارای یک گاز ایده آل با یک پیستون وزنه نشسته در بالا است ، به طوری که فشار اولیه روی گاز P1 = 10atm است. به منحنی 1 در زیر مراجعه کنید. ما به طور ناگهانی وزن را از بین می بریم تا فشار خارجی نصف شود ، یا P2a = 5atm. این امر منجر به انبساط آدیاباتیک غیر شبه ایستا (غیر قابل برگشت) در برابر فشار خارجی ثابت می شود. با استفاده از قوانین ایده آل گاز ، می توان حجم و دمای نهایی (نقطه 2a) را هنگام رسیدن به تعادل تعیین کرد ، با این فرض که حجم و دمای اولیه همانطور که برای نقطه 1 نشان داده شده است. کار انجام شده صرفاً فشار خارجی چند برابر تغییر حجم است.
ما می توانیم فرآیند برگشت ناپذیر را با انبساط آدیاباتیک برگشت پذیر مقایسه کنیم که در آن فشار نهایی همان فشار نهایی انبساط برگشت ناپذیر باشد. منحنی 2 را در زیر مشاهده کنید. آنچه خواهیم فهمید ، حجم نهایی و دمای نهایی انبساط آدیاباتیک برگشت پذیر (نقطه 2 منحنی) کمتر از انبساط برگشت ناپذیر است و کار انجام شده (منطقه زیر نمودار P-V) بیشتر از انبساط برگشت ناپذیر است.
حال می خواهیم سیستمی را که تحت انبساط برگشت ناپذیر (منحنی 1) قرار داشته است ، به حالت اولیه خود برگردانیم تا یک چرخه کامل به ما ارائه دهد. برای این کار می توان یک فشرده سازی ایزوباریک (فشار ثابت) گاز را از نقطه 2a به نقطه 2 انجام داد تا حجم و دمای آن کاهش یابد تا با حجم نهایی در انتهای انبساط برگشت پذیر مطابقت داشته باشد. این ما را به منحنی آدیاباتیک برگشت پذیر بازمی گرداند. اما همچنین نیاز به انتقال گرما از گاز به محیط اطراف دارد. بار دیگر ، این انتقال گرما معادل "کار از دست رفته" فرآیند برگشت ناپذیر خواهد بود. ما با انجام یک فشرده سازی آدیاباتیک برگشت پذیر از نقطه 2 به 1 فرآیند را کامل می کنیم تا سیستم را به حالت اولیه برگردانیم.
برای هر دو مورد نتیجه نهایی تولید آنتروپی انتقال گرما به محیط اطراف است

- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: هوافضا
ژیروسکوپ
اجازه دهید در بالا z^ جهت از پایه سازه به کره قرمز باشد ، و ایکس^ بردار واحد که از کره قرمز به سمت ژیروسکوپ می رود.
پیکانهای قرمز نشان دهنده سرعت قسمتهای مختلف ژیروسکوپ چرخان است. پیکانهای سبز نشان دهنده عملکرد موثر گرانش بر روی مرکز جرم میله است و نیروی متقابل مربوطه لولا را ارائه می دهد.
عملکرد ترکیبی دو فلش سبز باعث ایجاد گشتاور روی میله + سیستم ژیروسکوپ می شود و می خواهد آن را به پایین فشار دهد. اما تنها راه برای این اتفاق ، چرخش ژیروسکوپ در داخل استایکس^z^ سطح:
فلشهای فیروزه ای نیروهای مربوطه را نشان می دهد که این چرخش در نقاط بالا و پایین ژیروسکوپ ایجاد می کند. اکنون ، به یاد داشته باشید که فلشهای فیروزه ای نیروها را نشان می دهند ، در حالی که سرعت قرمزها. فلشهای فیروزه ای باعث تسریع در نقاط مختلف ژیروسکوپ می شوند. به طور خاص ، آنها فلش های قرمز را وادار به تغییر جهت می کنند. در مدل این برای نقاط بالا و پایین نشان داده شده است ، در حالی که فلشهای نارنجی بردارهای سرعت اصلاح شده را در آن نقاط بازنشانی می کنند.
همانطور که از آنجا مشاهده می کنید ، بردارهای جدید سرعت با مواردی که در هنگام تغییر جهت حرکت ژیروسکوپ به دنبال حرکت شتاب دادن ، مطابقت دارید. اساساً ، عملکرد نیروهای فیروزه ای روی سرعتهای قرمز همان چیزی است که باعث حرکت پیش دستی می شود.
اکنون برای تغذیه ، باید توجه داشته باشیم که فلش های فیروزه ای بالا در واقع به درستی ترسیم نشده اند. حرکت جیروسکوپ که به طرز صحیح تری سقوط می کند مطابقت دارد که فلشهای فیروزه ای کمی به سمت زمین متمایل شده اند. این البته قابل انتظار است: پس از همه ، اگر ژیروسکوپ چرخش نداشت ، فقط سقوط می کرد. به همین دلیل است حتی اگر حرکت تقدیمی وجود دارد، ژیروسکوپ کند به پایین کمی.
این شتاب به سمت زمین ، به دلیل همان مکانیزم توضیح داده شده در بالا ، نیز یک پیش دستی سریعتر را القا می کند. اما یک ترجیح شتاب آور اکنون به دلایلی شبیه به دلایل خود ترجیح ، موجب واکنش متقابل می شود.
یک حرکت شتاب دهنده به این معنی است که بردارهای نیرویی وجود دارد که ژیروسکوپ را به چرخش در داخل فشار می دهد ایکس^y^سطح. باز هم ، این مربوط به فشار دادن نقاط مختلف ژیروسکوپ به جهات مختلف است. در ادامه ، پیکان فیروزه ای نیروهایی را نشان می دهد که در دو نقطه عمل می کنند:انرژی جنبشی ان $ T=\frac{1}{2}I_1\omega_1^2+\frac{1}{2}I_2\omega_2^2+\frac{1}{2}I_3\omega_3^2$ با توجه به تنسور $I_{ij}=\sum m\left(r^2\delta_{ij}-r_ir_j\right) $ با توجه بردار$\vec{v}=\vec{\omega}\times\vec{r} $
باز هم ، این نیروهای فیروزه ای تغییر جهت جهت های قرمز متناظر را القا می کنند و فلش های نارنجی نشان می دهند که سرعت به زودی چه خواهد بود. همانطور که می بینید ، سرعتهای جدید مربوط به جهت حرکت ژیروسکوپ به سمت بالا است ، بنابراین پدیده "مقابله با سقوط" را ایجاد می کند که در این مورد ، تغذیه است.
یخوب مید.ونید ژیروسکوپ وسیله ای جهت حفظ جهت در راستای حفظ تعادل میباشد که از اصل بقای تکانه زاویهای استفاده میکند.یک ژیروسکوپ مکانیکی همیشه یک چرخ یا دیسک چرخنده با محور آزاد دارد که میتواند در هر جهتی بایستد. اما بهترین روش تحلیل ریاضی ان هست .محورهای مختصات XYZ را به صورت شکل زیر برای ژیروسکوپ رسم میکنیم تو این شکل g شتاب گرانش است. نقطه G مرکز جرم دیسک را نشان میدهد. محل تکیهگاه نیز با P نمایش داده میشود. مبدأ مختصات XYZ، نقطه P است. بردارهای J ،I و K بردارهای یکه هستند و به ترتیب جهت مثبت محورهای Y ،X و Z رابه ما نشون میدند.ابتدا من سرعت زاویه ای دیسک محاسبه کنم $\large\overrightarrow{\omega_w}=(\omega_s\sin\theta)\hat{J}+(\omega_s\cos\theta+\omega_p)\hat{K} $ از رابطه مشتق بگیرم $ \large\overrightarrow{a_w}=\frac{d[(\omega_s\sin\theta)\hat{J}]}{dt}+\frac{d[(\omega_s\cos\theta\:+\omega_p)\hat{K}]}{dt}$ خوب $\omega_s $ معلوم هست که صفر هست لذا رابطه ساده میشه$\large\overrightarrow{a}_w=-\omega_s\omega_p\sin\theta\:\hat{I} $ خوب سرعت زاویه ای میله $\large\overrightarrow{\omega}_r=\omega_p\:\hat{K} $ وچون سرعت زاویهای میله ثابت است و جهت آن هم تغییر نمیکند، شتاب زاویهای آن صفر هست حالا نیروها و گشتاورهای وارد به دیسک را برسی کنیم گشتاور در نقطه G و در راستای محور x را با Mx نشان دادهایم. گشتاورهای My و Mz نیز به طریقی مشابه تعریف میشه با قانون دوم نیوتن اشنا هستید همون رابطه معروف $\large\sum_{}F_X=F_{GX}=m_wa_{GX}\\~\\
\large\sum_{}F_Y=F_{GY}=m_wa_{GY}\\~\\
\large\sum_{}F_Z=F_{GZ}-m_wg=m_wa_{GZ} $جرم دیسک با mw نمایش داده شده است. aGX شتاب را در نقطه G و در راستای X نشان میدهم. شتابهای aGY و aGZ نیز به طوری مشابه و به ترتیب در جهتهای Y و Z تعریف میشه/$\large F_{GY}=m_wa_{GY} $خوب نقطه G روی یک مسیر افقی به شکل دایره و با سرعت ثابت حرکت میکند پس شتاب مماسی برابر صفر است.خوب شتاب گرا در جهت y $ \large a_{GY}=-{\omega_p}^2(L\sin\theta)$ هستش.لذا نیرو $ \large F_{GY}=-m_w{\omega_p}^2(L\sin\theta)$ خوب نقطه G با سرعت ثابت روی یک دایره افقی حرکت میکند، شتاب در راستای Z برابر با صفر است پس $\large F_{GZ}-m_wg=m_wa_{GZ}=0 $ و $ \large F_{GZ}=-m_w\:g$ حرکت اویلر را در جهت x برای جسم صلب به کاربرده و . این معادلات در دو جهت دیگر مساوی صفر هستند.$ \large \sum M_{Gx}=I_{Gx}\alpha_x-(I_{Gy}-I_{Gz})\omega_y\omega_z$ ببینید که نیروهای FGX ،FGY وFGZ حول نقطه G هیچ گشتاوری ایجاد نمیکنند. زیرا هر سه نیرو از نقطه G عبور کرده و طول بازوی گشتاور در آنها صفر است. در رابطه بالا، IGx ،IGy و IGz، به ترتیب ممانهای اینرسی را حول نقطه G در جهتهای y ،x و z نشان میدهد $ \large I_{Gx}=I_{Gz}=\frac{1}{4}m_wr^2$ لذا $ \large I_{Gy}=\frac{1}{2}m_wr^2$معادله حرکت اویلر در جهت x به دست خواهد آمد $ \large M_x=-\frac{1}{4}m_wr^2\omega_s\omega_p\sin\theta-\frac{1}{4}m_wr^2(\omega_s+\omega_p\cos\theta)\omega_p\sin\theta$ در این بخش گشتاورهای وارد شده به میله را حول نقطه P بررسی کنم $ \large \sum M_{Px}=I_{Px}a_x-(I_{Py}-I_{Pz})\omega_y\omega_z$سرعت و شتاب زاویهای میله در دستگاه xyz را میتوان به صورت زیر نوشت $ \large \omega_x=0\:\:,\:\:\omega_y=\omega_p\cos\theta\:\:,\:\:\omega_z=\omega_p\sin\theta\\~\\
\large a_x=a_y=a_z=0$ ،که IPy و IPz، به ترتیب ممانهای اینرسی میله را حول نقطه P در جهتهای y ،x و z نشان میدهند$\large I_{Px}=I_{Pz}=\frac{1}{3}m_rL^2\\~\\
\large I_{Py}=0 $ من معادله اویلر در جهت محور x مینویسم $ \large -m_rg\frac{L}{2}\sin\theta-F_{GZ}L\sin\theta+F_{GY}L\cos\theta-M_x\\
\large=\frac{1}{3}m_rL^2{\omega_p}^2\cos\theta\sin\theta$ ساده شده عبارت $\large {\omega_p}^2\cos\theta(\frac{1}{3}m_rL^2-\frac{1}{4}m_wr^2+m_wL^2)\\
\large=\frac{1}{2}m_wr^2\omega_s\omega_p-m_rg\frac{L}{2}-m_wgL $ هست پایداری ژیروسکوپ تکانه زاویهای تغییرات بردار تکانه زاویهای جسم صلب در بازه زمانی ti تاtf به صورت زیر محاسبه میشود. پارامتر Hf بردار تکانه زاویهای را در لحظه نهایی tf نشان میدهد. بردار تکانه زاویهای در لحظه اولیه ti نیز برابر با Hi است. بردار M همکه بیانگر گشتاورهای خارجی وارد به جسم صلب است.$ \large \sum \int_{ti}^{tf}\overrightarrow{M}dt={\overrightarrow{H}}_f-{\overrightarrow{H}}_i$
تکانه زاویهای بین زمانهای ti و tf با ΔH نشان داده شده است. خوب تحلیل اسپین میخواهم رابطهای برای ارتباط بین زاویه θ و بردارهای HG و ωs پیدا کنم. با استفاده از ضرب داخلی، رابطه زیر به راحتی به دستمیاد$ \large \cos\theta=\frac{{\overrightarrow{H}}_G.\hat{J}}{|{\overrightarrow{H}}_G|}$ خوب مشتق بگیرم $ \large\frac{\text{d}\theta}{\text{d}t}=-\frac{{\overrightarrow{H}}_G}{\sin\theta\:|{\overrightarrow{H}}_G|}(\frac{\text{d}\hat{j}}{\text{d}t})$ عبارت زیر جایگذاری کنم $(\frac{\text{d}\hat{j}}{\text{d}t})=\overrightarrow{\omega}\times\hat{j} $ از مفهوم ضرب خارجی $ \large\frac{\text{d}\theta}{\text{d}t}=-\frac{(I_z-I_x)\omega_z\omega_x}{\sin\theta\:|{\overrightarrow{H}}_G|}$ هنگامی که مقادیر Ix وIz با یکدیگر برابر باشند $\frac{\text{d}\theta}{\text{d}t} $ نیز صفر هست $\omega_x=\frac{\text{d}\theta}{\text{d}t}=0 $ و ωp را برحسب یکدیگر محاسبه کنیم. از آنجایی که زاویه θ همیشه ثابت است، تکانه زاویهای را میتوان به صورت زیر و در دستگاه مختصات xyz بیان کرد.$ \large {\overrightarrow{H}}_G=(|{\overrightarrow{H}_G}|\cos\theta)\hat{j}+(|{\overrightarrow{H}_G}|\sin\theta)\hat{k}$ لذا خوب دارم $\large\omega_s=\omega_p\cos\theta\frac{I_w-I_{Gy}}{I_{Gy}} $/vln0_6-حالا چرا هنگام چرخاندن یک فرفره به حالت ایستاده برمی گردد
جای این که مانند برخی از بالای صفحه ها به یک نقطه تیز در پایین برسد ، یک پایین گرد دارد. این اثر در تاپ هایی که شعاع انحنای بیشتری در پایین دارند ، بارزتر و چشمگیرتر است ، مانند حالت فوقانی بالای تیپ ، که دارای شعاع انحنای آنقدر بزرگ است که امکان دارد مرکز جرم بالای آن باشد در ارتفاعی کوچکتر از شعاع انحنا. در واقع ، مقاله هایی که من دیده ام نشان می دهد که چگونه اصطکاک کشویی باعث بالا آمدن مرکز جرم یک تاپ می شود ، به طور خاص آنالیز بالای تاپ را انجام می دهند.
تجزیه و تحلیل یک بالا به طور کلی ، از جمله اثرات اصطکاک ، کاملاً پیچیده است. برای ساده کردن تجزیه و تحلیل بسیار زیاد ، من فقط در یک لحظه به بالا نگاه می کنم که در آن بالا هیچ حرکت خطی ندارد ، و یک حرکت زاویه ای بسیار بزرگ دارد که دقیقاً در امتداد محور تقارن بالا قرار دارد.
همچنین گرانش را در این توضیح ساده قابل اغماض می دانم. گرانش باعث ایجاد یک گشتاور کاملاً افقی در قسمت بالایی می شود ، اما ما فقط به گشتاور علاقه مند هستیم که دارای یک مولفه عمودی باشد ، که باعث می شود تا بالا به طور قائم تر شود. در حقیقت ، اگر جاذبه سطح و میز را به هم نمی چسباند ، هیچ اصطکاک لغزشی در نقطه تماس بین این دو وجود نخواهد داشت ، اما ما به راحتی تصور خواهیم کرد که اصطکاک کشویی وجود دارد ، بدون در نظر گرفتن چگونگی اصطکاک کشویی مربوط به گرانش است.
از آنجا که بالای آن به جای پایین نوک تیز ، یک گرد دارد ، نقطه تماس بالای آن در P نیست ، بلکه در بعضی از نقاط C است. از فرضیات گفته شده در بالا ، در لحظه مورد علاقه P ثابت است. در مقابل ، از جهت$ \vec{L}$ ، در C سطح بالا به سمت بیننده در حال حرکت است ، مستقیم از صفحه نمودار به سمت بالا. اصطکاک کشویی یک نیروی$ \vec{F}_k$ (نشان داده نشده) در بالا در C ، در جهت مخالف حرکت بالا در آن نقطه است ، یعنی مستقیماً به سمت پایین
بردار موقعیت C از$\vec{X}_C $ است. نیروی $\vec{F}_k $ در بالا یک گشتاور در قسمت بالای مرکز جرم بالای آن تولید می کند ،
$\vec{\tau} = \vec{X}_C \times \vec{F}_k \,\, . $
گشتاور $\vec{\tau} $ را می توان به صورت زیر نوشت$ \vec{\tau}=\vec{\tau}_{\parallel}+\vec{\tau}_{\perp} \,\, ,$
جایی که$ \vec{\tau}_{\parallel}$ موازی$\vec{L} $ است و$ \vec{\tau}_{\perp}$ عمود بر $\vec{L} $ است.
گشتاور $ \vec{\tau}$ این است که حرکت زاویه ای $\vec{L} $ با زمان تغییر می کند ،$\frac{d\vec{L}}{dt} = \vec{\tau}=\vec{\tau}_{\parallel}+\vec{\tau}_{\perp} \,\, . $
اگه$\vec{\tau}_{\parallel} $در جهت مخالف $ \vec{L}$ قرار دارد ، بنابراین اثر$\vec{\tau}_{\parallel} $ کاهش بزرگی $ \vec{L}$ است ، به عنوان مثال ، کاهش سرعت بالا.
اگر قسمت بالای آن در فضای خالی باشد ، اثر $ \vec{\tau}_{\perp}$ چرخاندن قسمت بالای آن در جهت O در جهت ساعت در نمودار خواهد بود. با این وجود ، به دلیل محدودیتی که قسمت بالای صفحه با جدول در تماس است ، اثر $\vec{\tau}_{\perp} $ این است که O را از جدول بلند کرده و O را به بالاتر از C نزدیک کند.
بالا یک بدنه متقارن سفت و سخت است. معادلات حرکت یک جسم صلب در اطراف مرکز جرم آن توسط: .
$I_1\dot\Omega_1=(I_2-I_3)\Omega_2\Omega_3 $
$ I_2\dot\Omega_2=(I_3-I_1)\Omega_3\Omega_1$
$ I_3\dot\Omega_3=(I_1-I_2)\Omega_1\Omega_2$
فرض کنید که بالای سفت و سخت در مورد یک محور متقارن است (بگذارید بگوییم محور سوم) ، بنابراین ما داریم:
$I_1=I_2 $
و همچنین اینکه محور سوم باریک است:$I_3<I_1(or I_2) $
در این حالت معادله سوم حرکت دلالت دارد$ \Omega_3=\Omega = const.$
و به جای دو معادله دیگر ، بدست می آوریم:
$I_1\dot\Omega_1=(I_2-I_3)\Omega\Omega_2 $
$I_2\dot\Omega_2=(I_3-I_1)\Omega\Omega_1 $
با استفاده از مشتق اول معادله دوم با توجه به زمان و جایگزینی معادله دوم ، به دست می آوریم:$I_1I_2\ddot\Omega_2= \Omega^2 (I_3-I_1)(I_2-I_3)\Omega_2 $
این یک معادله یک نوسان ساز هارمونیک است:$ \ddot\Omega_2+k^2 \Omega_2 = 0$با$ k^2= - \frac{\Omega^2 (I_3-I_1)(I_2-I_3)}{I_1I_2}$
اکنون ، مشاهده کنید که k ^ 2> 0$ $از آنجا که $I_3-I_1<0 $ و$I_2-I_3>0 $ ، بنابراین ثابت فنر واقعی است و نوسان ساز هارمونیک پایدار است.
این اثر ژیروسکوپی نامیده می شود و بیان می کند که شیئی که در حال چرخش است دارای یک حرکت زاویه ای است $ \vec{L}$ بنابراین تمایل دارد که محور چرخش خود باقی بماند ،$\vec{L}=I\omega $ سریعتر می چرخد (ω بیشتر) بیشتر تمایل دارد که محور چرخش خود باقی بماند.
یک تصویر زیر را در نظر بگیرید ، یک چرخش با سرعت زاویه ای ω می چرخد ، بنابراین دارای یک حرکت زاویه ای$\vec{L} $ است ، سریعتر$ \vec{L}$ بیشتر می چرخد و بیشتر تمایل دارد که حرکت چرخشی خود را در مورد یک محور خاص حفظ کند ، توجه داشته باشید که وقتی سرعت آن کاهش می یابد (به دلیل نیروهای اصطکاک)$ \vec{L}$ کمتری دارد بنابراین ترجیح آن به دلیل سنگین شدن آن به سمت پایین افزایش می یابد.
توجه داشته باشید که نیروی گرانش باعث چرخش بالای چرخش ماشینی (پیش از چرخش چرخشی آن می شود) بنابراین می توانیم از این مشاهده نتیجه بگیریم که برای تغییر محور چرخش چرخش باید نیرویی اعمال شود ، بیشترین نیرویی که بیشتر از قبل از آن استفاده خواهد کرد محور چرخش (با فرض ثابت بودن L⃗). وقتی این نیرو برداشته شود ، به دلیل داشتن شتاب زاویه ای ، به طور طبیعی و بدون هیچ گونه مقدماتی به حالت اولیه برمی گردد.
به عنوان قانون اول نیوتون فکر کنید ، اما به جای حرکت ترجمه در حرکت چرخشی است.قانون اول نیوتون اظهار داشت:جسمی که در حال حرکت است تمایل دارد که در حرکت بماند و در یک خط مستقیم حرکت کند ، مگر اینکه توسط یک نیروی نامتعادل عمل کند.ما می توانیم این قانون را برای حرکت چرخشی دوباره ایجاد کنیم:جسمی که در حال چرخش است تمایل دارد که حرکات چرخشی در مورد یک محور خاص باقی بماند مگر اینکه توسط یک نیروی نامتعادل عمل کند.
جسمی که دارای یک حرکت انتقالی با سرعت v باشد به نیروی $ \vec{F}$ نیاز دارد تا جهت حرکت خود را به طور مشابه تغییر دهد شیئی که دارای سرعت زاویه ای ω است برای تغییر محور چرخشی خود به نیرو احتیاج دارد.گشتاور به عنوان گرایش نیرو برای چرخش یک جسم در مورد یک محور و از نظر ریاضی به عنوان یک محصول بردار (ضربدری) از فاصله و نیرو تعریف می شود:$ \vec{\tau}=\vec{r}\times\vec{F}$جایی که r فاصله ای از نقطه چرخش است و$\vec{F} $ به آن نیرو وارد می شود.
توجه داشته باشید که گشتاور یک بردار است و این بردار در تصویر زیر نشان داده شده است:
چرخش بالا تقریباً عمودی می شود زیرا دارای حرکت زاویه ای است و این بدان معناست که اگر جسمی بچرخد در مقابل محور چرخش خود مقدمه گرفته و سریعتر بچرخد در مقابل این مقدمه مقاومت می کند تا اتفاق بیفتد ، بنابراین اگر هنوز آن را برعکس کردم می چرخد با همان سرعت زاویه ای به سرعت صفر باز می گردد ، سریعتر می چرخد سریعتر به حالت اولیه خود باز می گردد.
برای توضیح این موضوع از نظر ریاضی ، یک در حال چرخش روی زمین با سرعت زاویه ای ω در نظر گرفته شده است و دارای سرعت زاویه ای شیب ω پی و زاویه شیب دار
حرکت زاویه ای آن به صورت زیر تعریف می شود:$\vec{L}= \vec{\omega} I $
بگویید چرخش بالای Δθ چرخانده و تغییر آن در حرکت زاویه ای ΔL است.
سپس می توانیم Δθ را به صورت زیر بیان کنیم:$ \Delta \theta \approx \frac{\Delta L}{L sin(\phi)}$
سرعت زاویه ای حق تقدم را می توان به شرح زیر بیان کرد:$\omega_p = \frac{\Delta \theta}{\Delta t} $
اکنون می توانیم معادله اول را در این معادله جایگزین کنیم.$\omega_p = \frac{\Delta L}{\Delta t L sin(\phi)} $
گشتاور به عنوان تغییر در حرکت زاویه ای تعریف می شود:
$\frac{\Delta L}{\Delta t}= I \vec{\alpha} = \tau $
حالا این را در معادله قبلی جایگزین می کنیم:$\omega_p = \frac{\tau}{L sin(\phi)} $
و فرمول زیر را دریافت می کنیم:$\omega_p = \frac{\vec{F}r}{L sin(\phi)} $
از این معادله می توان دریافت که اگر نیرویی را روی جسمی در حال چرخش وارد کنیم ، ωp آن افزایش می یابد زیرا با نیروی اعمال شده متناسب است. اگر نیروی اعمال شده صفر باشد ، ωp نیز صفر می شود ، بنابراین دیگر سرعت زاویه ای فوق العاده ای نخواهد داشت بنابراین دوباره به صورت ایستاده ایستاده است.
اجازه دهید در بالا z^ جهت از پایه سازه به کره قرمز باشد ، و ایکس^ بردار واحد که از کره قرمز به سمت ژیروسکوپ می رود.
پیکانهای قرمز نشان دهنده سرعت قسمتهای مختلف ژیروسکوپ چرخان است. پیکانهای سبز نشان دهنده عملکرد موثر گرانش بر روی مرکز جرم میله است و نیروی متقابل مربوطه لولا را ارائه می دهد.
عملکرد ترکیبی دو فلش سبز باعث ایجاد گشتاور روی میله + سیستم ژیروسکوپ می شود و می خواهد آن را به پایین فشار دهد. اما تنها راه برای این اتفاق ، چرخش ژیروسکوپ در داخل استایکس^z^ سطح:
فلشهای فیروزه ای نیروهای مربوطه را نشان می دهد که این چرخش در نقاط بالا و پایین ژیروسکوپ ایجاد می کند. اکنون ، به یاد داشته باشید که فلشهای فیروزه ای نیروها را نشان می دهند ، در حالی که سرعت قرمزها. فلشهای فیروزه ای باعث تسریع در نقاط مختلف ژیروسکوپ می شوند. به طور خاص ، آنها فلش های قرمز را وادار به تغییر جهت می کنند. در مدل این برای نقاط بالا و پایین نشان داده شده است ، در حالی که فلشهای نارنجی بردارهای سرعت اصلاح شده را در آن نقاط بازنشانی می کنند.
همانطور که از آنجا مشاهده می کنید ، بردارهای جدید سرعت با مواردی که در هنگام تغییر جهت حرکت ژیروسکوپ به دنبال حرکت شتاب دادن ، مطابقت دارید. اساساً ، عملکرد نیروهای فیروزه ای روی سرعتهای قرمز همان چیزی است که باعث حرکت پیش دستی می شود.
اکنون برای تغذیه ، باید توجه داشته باشیم که فلش های فیروزه ای بالا در واقع به درستی ترسیم نشده اند. حرکت جیروسکوپ که به طرز صحیح تری سقوط می کند مطابقت دارد که فلشهای فیروزه ای کمی به سمت زمین متمایل شده اند. این البته قابل انتظار است: پس از همه ، اگر ژیروسکوپ چرخش نداشت ، فقط سقوط می کرد. به همین دلیل است حتی اگر حرکت تقدیمی وجود دارد، ژیروسکوپ کند به پایین کمی.
این شتاب به سمت زمین ، به دلیل همان مکانیزم توضیح داده شده در بالا ، نیز یک پیش دستی سریعتر را القا می کند. اما یک ترجیح شتاب آور اکنون به دلایلی شبیه به دلایل خود ترجیح ، موجب واکنش متقابل می شود.
یک حرکت شتاب دهنده به این معنی است که بردارهای نیرویی وجود دارد که ژیروسکوپ را به چرخش در داخل فشار می دهد ایکس^y^سطح. باز هم ، این مربوط به فشار دادن نقاط مختلف ژیروسکوپ به جهات مختلف است. در ادامه ، پیکان فیروزه ای نیروهایی را نشان می دهد که در دو نقطه عمل می کنند:انرژی جنبشی ان $ T=\frac{1}{2}I_1\omega_1^2+\frac{1}{2}I_2\omega_2^2+\frac{1}{2}I_3\omega_3^2$ با توجه به تنسور $I_{ij}=\sum m\left(r^2\delta_{ij}-r_ir_j\right) $ با توجه بردار$\vec{v}=\vec{\omega}\times\vec{r} $
باز هم ، این نیروهای فیروزه ای تغییر جهت جهت های قرمز متناظر را القا می کنند و فلش های نارنجی نشان می دهند که سرعت به زودی چه خواهد بود. همانطور که می بینید ، سرعتهای جدید مربوط به جهت حرکت ژیروسکوپ به سمت بالا است ، بنابراین پدیده "مقابله با سقوط" را ایجاد می کند که در این مورد ، تغذیه است.
یخوب مید.ونید ژیروسکوپ وسیله ای جهت حفظ جهت در راستای حفظ تعادل میباشد که از اصل بقای تکانه زاویهای استفاده میکند.یک ژیروسکوپ مکانیکی همیشه یک چرخ یا دیسک چرخنده با محور آزاد دارد که میتواند در هر جهتی بایستد. اما بهترین روش تحلیل ریاضی ان هست .محورهای مختصات XYZ را به صورت شکل زیر برای ژیروسکوپ رسم میکنیم تو این شکل g شتاب گرانش است. نقطه G مرکز جرم دیسک را نشان میدهد. محل تکیهگاه نیز با P نمایش داده میشود. مبدأ مختصات XYZ، نقطه P است. بردارهای J ،I و K بردارهای یکه هستند و به ترتیب جهت مثبت محورهای Y ،X و Z رابه ما نشون میدند.ابتدا من سرعت زاویه ای دیسک محاسبه کنم $\large\overrightarrow{\omega_w}=(\omega_s\sin\theta)\hat{J}+(\omega_s\cos\theta+\omega_p)\hat{K} $ از رابطه مشتق بگیرم $ \large\overrightarrow{a_w}=\frac{d[(\omega_s\sin\theta)\hat{J}]}{dt}+\frac{d[(\omega_s\cos\theta\:+\omega_p)\hat{K}]}{dt}$ خوب $\omega_s $ معلوم هست که صفر هست لذا رابطه ساده میشه$\large\overrightarrow{a}_w=-\omega_s\omega_p\sin\theta\:\hat{I} $ خوب سرعت زاویه ای میله $\large\overrightarrow{\omega}_r=\omega_p\:\hat{K} $ وچون سرعت زاویهای میله ثابت است و جهت آن هم تغییر نمیکند، شتاب زاویهای آن صفر هست حالا نیروها و گشتاورهای وارد به دیسک را برسی کنیم گشتاور در نقطه G و در راستای محور x را با Mx نشان دادهایم. گشتاورهای My و Mz نیز به طریقی مشابه تعریف میشه با قانون دوم نیوتن اشنا هستید همون رابطه معروف $\large\sum_{}F_X=F_{GX}=m_wa_{GX}\\~\\
\large\sum_{}F_Y=F_{GY}=m_wa_{GY}\\~\\
\large\sum_{}F_Z=F_{GZ}-m_wg=m_wa_{GZ} $جرم دیسک با mw نمایش داده شده است. aGX شتاب را در نقطه G و در راستای X نشان میدهم. شتابهای aGY و aGZ نیز به طوری مشابه و به ترتیب در جهتهای Y و Z تعریف میشه/$\large F_{GY}=m_wa_{GY} $خوب نقطه G روی یک مسیر افقی به شکل دایره و با سرعت ثابت حرکت میکند پس شتاب مماسی برابر صفر است.خوب شتاب گرا در جهت y $ \large a_{GY}=-{\omega_p}^2(L\sin\theta)$ هستش.لذا نیرو $ \large F_{GY}=-m_w{\omega_p}^2(L\sin\theta)$ خوب نقطه G با سرعت ثابت روی یک دایره افقی حرکت میکند، شتاب در راستای Z برابر با صفر است پس $\large F_{GZ}-m_wg=m_wa_{GZ}=0 $ و $ \large F_{GZ}=-m_w\:g$ حرکت اویلر را در جهت x برای جسم صلب به کاربرده و . این معادلات در دو جهت دیگر مساوی صفر هستند.$ \large \sum M_{Gx}=I_{Gx}\alpha_x-(I_{Gy}-I_{Gz})\omega_y\omega_z$ ببینید که نیروهای FGX ،FGY وFGZ حول نقطه G هیچ گشتاوری ایجاد نمیکنند. زیرا هر سه نیرو از نقطه G عبور کرده و طول بازوی گشتاور در آنها صفر است. در رابطه بالا، IGx ،IGy و IGz، به ترتیب ممانهای اینرسی را حول نقطه G در جهتهای y ،x و z نشان میدهد $ \large I_{Gx}=I_{Gz}=\frac{1}{4}m_wr^2$ لذا $ \large I_{Gy}=\frac{1}{2}m_wr^2$معادله حرکت اویلر در جهت x به دست خواهد آمد $ \large M_x=-\frac{1}{4}m_wr^2\omega_s\omega_p\sin\theta-\frac{1}{4}m_wr^2(\omega_s+\omega_p\cos\theta)\omega_p\sin\theta$ در این بخش گشتاورهای وارد شده به میله را حول نقطه P بررسی کنم $ \large \sum M_{Px}=I_{Px}a_x-(I_{Py}-I_{Pz})\omega_y\omega_z$سرعت و شتاب زاویهای میله در دستگاه xyz را میتوان به صورت زیر نوشت $ \large \omega_x=0\:\:,\:\:\omega_y=\omega_p\cos\theta\:\:,\:\:\omega_z=\omega_p\sin\theta\\~\\
\large a_x=a_y=a_z=0$ ،که IPy و IPz، به ترتیب ممانهای اینرسی میله را حول نقطه P در جهتهای y ،x و z نشان میدهند$\large I_{Px}=I_{Pz}=\frac{1}{3}m_rL^2\\~\\
\large I_{Py}=0 $ من معادله اویلر در جهت محور x مینویسم $ \large -m_rg\frac{L}{2}\sin\theta-F_{GZ}L\sin\theta+F_{GY}L\cos\theta-M_x\\
\large=\frac{1}{3}m_rL^2{\omega_p}^2\cos\theta\sin\theta$ ساده شده عبارت $\large {\omega_p}^2\cos\theta(\frac{1}{3}m_rL^2-\frac{1}{4}m_wr^2+m_wL^2)\\
\large=\frac{1}{2}m_wr^2\omega_s\omega_p-m_rg\frac{L}{2}-m_wgL $ هست پایداری ژیروسکوپ تکانه زاویهای تغییرات بردار تکانه زاویهای جسم صلب در بازه زمانی ti تاtf به صورت زیر محاسبه میشود. پارامتر Hf بردار تکانه زاویهای را در لحظه نهایی tf نشان میدهد. بردار تکانه زاویهای در لحظه اولیه ti نیز برابر با Hi است. بردار M همکه بیانگر گشتاورهای خارجی وارد به جسم صلب است.$ \large \sum \int_{ti}^{tf}\overrightarrow{M}dt={\overrightarrow{H}}_f-{\overrightarrow{H}}_i$
تکانه زاویهای بین زمانهای ti و tf با ΔH نشان داده شده است. خوب تحلیل اسپین میخواهم رابطهای برای ارتباط بین زاویه θ و بردارهای HG و ωs پیدا کنم. با استفاده از ضرب داخلی، رابطه زیر به راحتی به دستمیاد$ \large \cos\theta=\frac{{\overrightarrow{H}}_G.\hat{J}}{|{\overrightarrow{H}}_G|}$ خوب مشتق بگیرم $ \large\frac{\text{d}\theta}{\text{d}t}=-\frac{{\overrightarrow{H}}_G}{\sin\theta\:|{\overrightarrow{H}}_G|}(\frac{\text{d}\hat{j}}{\text{d}t})$ عبارت زیر جایگذاری کنم $(\frac{\text{d}\hat{j}}{\text{d}t})=\overrightarrow{\omega}\times\hat{j} $ از مفهوم ضرب خارجی $ \large\frac{\text{d}\theta}{\text{d}t}=-\frac{(I_z-I_x)\omega_z\omega_x}{\sin\theta\:|{\overrightarrow{H}}_G|}$ هنگامی که مقادیر Ix وIz با یکدیگر برابر باشند $\frac{\text{d}\theta}{\text{d}t} $ نیز صفر هست $\omega_x=\frac{\text{d}\theta}{\text{d}t}=0 $ و ωp را برحسب یکدیگر محاسبه کنیم. از آنجایی که زاویه θ همیشه ثابت است، تکانه زاویهای را میتوان به صورت زیر و در دستگاه مختصات xyz بیان کرد.$ \large {\overrightarrow{H}}_G=(|{\overrightarrow{H}_G}|\cos\theta)\hat{j}+(|{\overrightarrow{H}_G}|\sin\theta)\hat{k}$ لذا خوب دارم $\large\omega_s=\omega_p\cos\theta\frac{I_w-I_{Gy}}{I_{Gy}} $/vln0_6-حالا چرا هنگام چرخاندن یک فرفره به حالت ایستاده برمی گردد
جای این که مانند برخی از بالای صفحه ها به یک نقطه تیز در پایین برسد ، یک پایین گرد دارد. این اثر در تاپ هایی که شعاع انحنای بیشتری در پایین دارند ، بارزتر و چشمگیرتر است ، مانند حالت فوقانی بالای تیپ ، که دارای شعاع انحنای آنقدر بزرگ است که امکان دارد مرکز جرم بالای آن باشد در ارتفاعی کوچکتر از شعاع انحنا. در واقع ، مقاله هایی که من دیده ام نشان می دهد که چگونه اصطکاک کشویی باعث بالا آمدن مرکز جرم یک تاپ می شود ، به طور خاص آنالیز بالای تاپ را انجام می دهند.
تجزیه و تحلیل یک بالا به طور کلی ، از جمله اثرات اصطکاک ، کاملاً پیچیده است. برای ساده کردن تجزیه و تحلیل بسیار زیاد ، من فقط در یک لحظه به بالا نگاه می کنم که در آن بالا هیچ حرکت خطی ندارد ، و یک حرکت زاویه ای بسیار بزرگ دارد که دقیقاً در امتداد محور تقارن بالا قرار دارد.
همچنین گرانش را در این توضیح ساده قابل اغماض می دانم. گرانش باعث ایجاد یک گشتاور کاملاً افقی در قسمت بالایی می شود ، اما ما فقط به گشتاور علاقه مند هستیم که دارای یک مولفه عمودی باشد ، که باعث می شود تا بالا به طور قائم تر شود. در حقیقت ، اگر جاذبه سطح و میز را به هم نمی چسباند ، هیچ اصطکاک لغزشی در نقطه تماس بین این دو وجود نخواهد داشت ، اما ما به راحتی تصور خواهیم کرد که اصطکاک کشویی وجود دارد ، بدون در نظر گرفتن چگونگی اصطکاک کشویی مربوط به گرانش است.
از آنجا که بالای آن به جای پایین نوک تیز ، یک گرد دارد ، نقطه تماس بالای آن در P نیست ، بلکه در بعضی از نقاط C است. از فرضیات گفته شده در بالا ، در لحظه مورد علاقه P ثابت است. در مقابل ، از جهت$ \vec{L}$ ، در C سطح بالا به سمت بیننده در حال حرکت است ، مستقیم از صفحه نمودار به سمت بالا. اصطکاک کشویی یک نیروی$ \vec{F}_k$ (نشان داده نشده) در بالا در C ، در جهت مخالف حرکت بالا در آن نقطه است ، یعنی مستقیماً به سمت پایین
بردار موقعیت C از$\vec{X}_C $ است. نیروی $\vec{F}_k $ در بالا یک گشتاور در قسمت بالای مرکز جرم بالای آن تولید می کند ،
$\vec{\tau} = \vec{X}_C \times \vec{F}_k \,\, . $
گشتاور $\vec{\tau} $ را می توان به صورت زیر نوشت$ \vec{\tau}=\vec{\tau}_{\parallel}+\vec{\tau}_{\perp} \,\, ,$
جایی که$ \vec{\tau}_{\parallel}$ موازی$\vec{L} $ است و$ \vec{\tau}_{\perp}$ عمود بر $\vec{L} $ است.
گشتاور $ \vec{\tau}$ این است که حرکت زاویه ای $\vec{L} $ با زمان تغییر می کند ،$\frac{d\vec{L}}{dt} = \vec{\tau}=\vec{\tau}_{\parallel}+\vec{\tau}_{\perp} \,\, . $
اگه$\vec{\tau}_{\parallel} $در جهت مخالف $ \vec{L}$ قرار دارد ، بنابراین اثر$\vec{\tau}_{\parallel} $ کاهش بزرگی $ \vec{L}$ است ، به عنوان مثال ، کاهش سرعت بالا.
اگر قسمت بالای آن در فضای خالی باشد ، اثر $ \vec{\tau}_{\perp}$ چرخاندن قسمت بالای آن در جهت O در جهت ساعت در نمودار خواهد بود. با این وجود ، به دلیل محدودیتی که قسمت بالای صفحه با جدول در تماس است ، اثر $\vec{\tau}_{\perp} $ این است که O را از جدول بلند کرده و O را به بالاتر از C نزدیک کند.
بالا یک بدنه متقارن سفت و سخت است. معادلات حرکت یک جسم صلب در اطراف مرکز جرم آن توسط: .
$I_1\dot\Omega_1=(I_2-I_3)\Omega_2\Omega_3 $
$ I_2\dot\Omega_2=(I_3-I_1)\Omega_3\Omega_1$
$ I_3\dot\Omega_3=(I_1-I_2)\Omega_1\Omega_2$
فرض کنید که بالای سفت و سخت در مورد یک محور متقارن است (بگذارید بگوییم محور سوم) ، بنابراین ما داریم:
$I_1=I_2 $
و همچنین اینکه محور سوم باریک است:$I_3<I_1(or I_2) $
در این حالت معادله سوم حرکت دلالت دارد$ \Omega_3=\Omega = const.$
و به جای دو معادله دیگر ، بدست می آوریم:
$I_1\dot\Omega_1=(I_2-I_3)\Omega\Omega_2 $
$I_2\dot\Omega_2=(I_3-I_1)\Omega\Omega_1 $
با استفاده از مشتق اول معادله دوم با توجه به زمان و جایگزینی معادله دوم ، به دست می آوریم:$I_1I_2\ddot\Omega_2= \Omega^2 (I_3-I_1)(I_2-I_3)\Omega_2 $
این یک معادله یک نوسان ساز هارمونیک است:$ \ddot\Omega_2+k^2 \Omega_2 = 0$با$ k^2= - \frac{\Omega^2 (I_3-I_1)(I_2-I_3)}{I_1I_2}$
اکنون ، مشاهده کنید که k ^ 2> 0$ $از آنجا که $I_3-I_1<0 $ و$I_2-I_3>0 $ ، بنابراین ثابت فنر واقعی است و نوسان ساز هارمونیک پایدار است.
این اثر ژیروسکوپی نامیده می شود و بیان می کند که شیئی که در حال چرخش است دارای یک حرکت زاویه ای است $ \vec{L}$ بنابراین تمایل دارد که محور چرخش خود باقی بماند ،$\vec{L}=I\omega $ سریعتر می چرخد (ω بیشتر) بیشتر تمایل دارد که محور چرخش خود باقی بماند.
یک تصویر زیر را در نظر بگیرید ، یک چرخش با سرعت زاویه ای ω می چرخد ، بنابراین دارای یک حرکت زاویه ای$\vec{L} $ است ، سریعتر$ \vec{L}$ بیشتر می چرخد و بیشتر تمایل دارد که حرکت چرخشی خود را در مورد یک محور خاص حفظ کند ، توجه داشته باشید که وقتی سرعت آن کاهش می یابد (به دلیل نیروهای اصطکاک)$ \vec{L}$ کمتری دارد بنابراین ترجیح آن به دلیل سنگین شدن آن به سمت پایین افزایش می یابد.
توجه داشته باشید که نیروی گرانش باعث چرخش بالای چرخش ماشینی (پیش از چرخش چرخشی آن می شود) بنابراین می توانیم از این مشاهده نتیجه بگیریم که برای تغییر محور چرخش چرخش باید نیرویی اعمال شود ، بیشترین نیرویی که بیشتر از قبل از آن استفاده خواهد کرد محور چرخش (با فرض ثابت بودن L⃗). وقتی این نیرو برداشته شود ، به دلیل داشتن شتاب زاویه ای ، به طور طبیعی و بدون هیچ گونه مقدماتی به حالت اولیه برمی گردد.
به عنوان قانون اول نیوتون فکر کنید ، اما به جای حرکت ترجمه در حرکت چرخشی است.قانون اول نیوتون اظهار داشت:جسمی که در حال حرکت است تمایل دارد که در حرکت بماند و در یک خط مستقیم حرکت کند ، مگر اینکه توسط یک نیروی نامتعادل عمل کند.ما می توانیم این قانون را برای حرکت چرخشی دوباره ایجاد کنیم:جسمی که در حال چرخش است تمایل دارد که حرکات چرخشی در مورد یک محور خاص باقی بماند مگر اینکه توسط یک نیروی نامتعادل عمل کند.
جسمی که دارای یک حرکت انتقالی با سرعت v باشد به نیروی $ \vec{F}$ نیاز دارد تا جهت حرکت خود را به طور مشابه تغییر دهد شیئی که دارای سرعت زاویه ای ω است برای تغییر محور چرخشی خود به نیرو احتیاج دارد.گشتاور به عنوان گرایش نیرو برای چرخش یک جسم در مورد یک محور و از نظر ریاضی به عنوان یک محصول بردار (ضربدری) از فاصله و نیرو تعریف می شود:$ \vec{\tau}=\vec{r}\times\vec{F}$جایی که r فاصله ای از نقطه چرخش است و$\vec{F} $ به آن نیرو وارد می شود.
توجه داشته باشید که گشتاور یک بردار است و این بردار در تصویر زیر نشان داده شده است:
چرخش بالا تقریباً عمودی می شود زیرا دارای حرکت زاویه ای است و این بدان معناست که اگر جسمی بچرخد در مقابل محور چرخش خود مقدمه گرفته و سریعتر بچرخد در مقابل این مقدمه مقاومت می کند تا اتفاق بیفتد ، بنابراین اگر هنوز آن را برعکس کردم می چرخد با همان سرعت زاویه ای به سرعت صفر باز می گردد ، سریعتر می چرخد سریعتر به حالت اولیه خود باز می گردد.
برای توضیح این موضوع از نظر ریاضی ، یک در حال چرخش روی زمین با سرعت زاویه ای ω در نظر گرفته شده است و دارای سرعت زاویه ای شیب ω پی و زاویه شیب دار
حرکت زاویه ای آن به صورت زیر تعریف می شود:$\vec{L}= \vec{\omega} I $
بگویید چرخش بالای Δθ چرخانده و تغییر آن در حرکت زاویه ای ΔL است.
سپس می توانیم Δθ را به صورت زیر بیان کنیم:$ \Delta \theta \approx \frac{\Delta L}{L sin(\phi)}$
سرعت زاویه ای حق تقدم را می توان به شرح زیر بیان کرد:$\omega_p = \frac{\Delta \theta}{\Delta t} $
اکنون می توانیم معادله اول را در این معادله جایگزین کنیم.$\omega_p = \frac{\Delta L}{\Delta t L sin(\phi)} $
گشتاور به عنوان تغییر در حرکت زاویه ای تعریف می شود:
$\frac{\Delta L}{\Delta t}= I \vec{\alpha} = \tau $
حالا این را در معادله قبلی جایگزین می کنیم:$\omega_p = \frac{\tau}{L sin(\phi)} $
و فرمول زیر را دریافت می کنیم:$\omega_p = \frac{\vec{F}r}{L sin(\phi)} $
از این معادله می توان دریافت که اگر نیرویی را روی جسمی در حال چرخش وارد کنیم ، ωp آن افزایش می یابد زیرا با نیروی اعمال شده متناسب است. اگر نیروی اعمال شده صفر باشد ، ωp نیز صفر می شود ، بنابراین دیگر سرعت زاویه ای فوق العاده ای نخواهد داشت بنابراین دوباره به صورت ایستاده ایستاده است.

- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: هوافضا
اگر به یک جسم جامد به اندازه کافی نیرو وارد شود، مقداری تغییر شکل در آن رخ خواهد داد. در صورت «الاستیک» (Elastic) یا اصطلاحاً کشسان بودن ماده، شکل و اندازه جسم پس از حذف نیرو به حالت اولیه خود بازمیگردد. دلایل فیزیکی رفتار الاستیک در مواد مختلف تقریباً متفاوت است. هنگام اعمال نیرو بر روی فلزات، اندازه و شکل ماده از طریق شبکه اتمی آنها تغییر میکند (افزایش سطح انرژی). با حذف نیرو، شبکه به سطح انرژی پایینتر بازمیگردد. برای مواد لاستیکی و دیگر پلیمرها، کشش زنجیرههای پلیمری در هنگام اعمال نیرو باعث ایجاد خاصیت الاستیسیته میشود.«الاستیسیته کامل» (Perfect Elasticity)، معیاری برای تخمین الاستیسیته مواد در دنیای واقعی است. فیبر کوارتز، بیشترین خاصیت الاستیک در میان مواد مختلف را دارد. با این وجود، حتی این ماده یک جسم الاستیک کامل نیست. از اینرو، ماده کاملاً الاستیک تنها یک تعریف ایدئال در نظر گرفته میشود. اکثر مواد دارای الاستیسیته، تنها در صورت ایجاد تغییر شکلهای بسیار کوچک رفتار کاملاً الاستیک را از خود بروز میدهند.
هنگامی که یک ماده کاملاً الاستیک تغییر شکل می یابد ، انرژی مرتبط با فشار به عنوان انرژی پتانسیل الاستیک در بدن ذخیره می شود ، به آن انرژی کرنش گفته می شود. با از بین بردن نیروهای تغییر شکل دهنده ، بدن کاملاً شکل ، اندازه و پیکربندی اصلی خود را از دست می دهد و دیگر از بین رفتن گرما نیست. با این حال ، هیچ چیز کاملاً الاستیک نیست! هنگامی که یک ماده جزئی الاستیک (به عنوان مثال ، یک نوار لاستیکی) تغییر شکل می یابد ، حتی در صورت خارج شدن نیروهای تغییر شکل دهنده ، همیشه یک تغییر شکل باقی مانده وجود دارد. پسماند و بخشی از انرژی تبدیل شده به گرما را نشان می دهد. در اینجا یک مرجع سریع است.این تغییر شکل باقیمانده چگونه مسئول گرم شدن مواد است؟$dT=\frac{T}{C_V}\Big[dS-\Big(\frac{\partial P}{\partial T}\Big)_V dV\Big], $
ما توجه داریم که تغییر دما به دلیل تغییر در حجم V یا تغییر در آنتروپی S یا هر دو ایجاد می شود. آیا می توانیم با استفاده از این موضوع بفهمیم چه خبر است؟
حدس من این است که برای تغییر شکل الاستیک یک ماده کاملاً الاستیک ، در طول فرآیند بارگیری dT منفی است زیرا dV> 0 و در هنگام تخلیه dT مثبت است زیرا dV <0. در کل چرخه ، وقتی سیستم به حالت اولیه خود می رسد ، گرم نمی شودیک ماده الاستیک تا حدودی (به عنوان مثال ، ماده ویسکوالاستیک) ترکیبی از رفتار الاستیک و چسبناک را نشان می دهد ، و این قسمت چسبناک است که مسئول افزایش انرژی داخلی (مورد آدیاباتیک) یا انتشار گرما است (مورد همدما).
یک فنر و یک دمپر (داشپات) را بصورت سریالی تصور کنید. هنگامی که ترکیب کشیده می شود ، فنر و دمپر هر دو گسترش می یابند ، اما امتداد دمپر مسئول اتلاف انرژی مکانیکی به هر دو انرژی داخلی گرما است. بنابراین ، هنگامی که نیروی گسترش دهنده ترکیب آزاد می شود ، فنر می تواند به طول اصلی خود بازگردد ، اما طول جدید دمپر قفل می شود. بنابراین ترکیب کلی برخی از پسوندهای باقیمانده را حفظ می کند ، و مقداری از انرژی مکانیکی توسط دمپر
و ما P را به عنوان فشار و ... را به عنوان انرژی درونی یک ماده جامد تعریف می کنیم. اینها را می توان به دو قسمت تقسیم کرد: یک قسمت الاستیک و یک قسمت حرارتی. $P_{c} $ و $ \epsilon_{c}$ فقط به چگالی ماده ، ρ یا حجم خاص ، $V = 1 / ρ$ بستگی دارد. اینها برابر با فشار کل و انرژی داخلی خاص در صفر مطلق یا T = 0 K هستند. فرض کنیم که حجم ویژه در T = 0 و P = 0 توسط Voc داده شود ، که فقط ~ 1-2٪ کوچکتر از حجم ویژه در STP ، Vo ، برای بیشتر فلزات.
منحنی انرژی پتانسیل یا منحنی تعریف کننده ϵc ، از نظر کیفی شبیه منحنی انرژی پتانسیل است که تعامل بین دو اتم را به عنوان تابعی از فاصله هسته ای ، Δxn توصیف می کند. وقتی V> Voc ، نیروهای جذاب غالب می شوند اما با افزایش فواصل درون هسته ای به سرعت سقوط می کنند (به عنوان مثال ، با افزایش T). به عبارت دیگر ، وقتی اتمها از هم دورتر شوند ، asc به طور مجانبی تا مقداری مقدار U افزایش می یابد ، که تقریباً انرژی اتصال اتمها در بدن است. بنابراین ، U انرژی مورد نیاز برای حذف همه اتمها از جسم تا بی نهایت را نشان می دهد ، که تقریباً برابر با گرمای تبخیر ماده است ... بنابراین ، ϵc (V) → U به عنوان $ \Delta x_{n} \rightarrow \sim 2$.
برعکس ، اگر نیروهای V <Voc باشد نیروهای دافعه مسلط می شوند. با در نظر گرفتن این که کار انجام شده با فشرده سازی مواد برابر با افزایش در خواهد بود ، می توانیم این مقدار را کمی تعریف کنیم$P_{c} = - \left( \frac{ d \epsilon_{c} }{ d V } \right)_{T = 0} $
اگر از اولین هویت ترمودینامیکی بالا استفاده کنیم ، دو نتیجه خواهیم یافت ، یکی برای پارامترهای الاستیک و دیگری برای حرارتی:
$\begin{align}
\left( \frac{ \partial \epsilon_{c} }{ \partial V } \right)_{T} & = \frac{ d \epsilon_{c} }{ d V } = - P_{c}\left( V \right) \tag{2a} \\
\left( \frac{ \partial \epsilon_{T} }{ \partial V } \right)_{T} & = 0 = T \left( \frac{ \partial P_{T} }{ \partial T } \right)_{V} - P_{T} \tag{2b}
\end{align} $
من شکل خطی اونو که ساده هست بیان میکنم ترمودینامیک یک فنر منفرد در پتانسیل جاذبه
من سعی می کنم این مشکل ترمودینامیک را حل کنم. یک چشمه ثابت k الاستیک وجود دارد که در موقعیت تعادل آن به جرم m متصل است $\begin{equation}
x_{0}=\frac{mg}{k}
\end{equation} $
ناگهان در انتهای فنر جرم جدید M اضافه می کنیم بنابراین فنر برای مدتی نوسان می کند تا اینکه در موقعیت تعادل جدیدی قرار بگیرد. این در دمای ثابت T و در تماس با دمای هوا اتفاق می افتد$\begin{equation}
x_f=\frac{(m+M)g}{k}
\end{equation} $سوال من این است: در طی آن فرایند چقدر گرما آزاد یا جذب فنر می شود و میزان آنتروپی جهان چقدر افزایش می یابد؟
مشکل من این است که من دو روش جایگزین برای این کار دارم و آنها دو نتیجه می دهند. علاوه بر این ، ظرایف خاصی از ترمودینامیک وجود دارد که مرا گیج می کند. بگذارید دو روش را توضیح دهم:انرژی که سیستم از دست داده است برابر است با:$\begin{equation}
\begin{aligned}
\Delta E &= E_f-E_i \\ &= -\frac{g^2(m+M)^2}{k}+\frac{g^2m^2}{k}
\end{aligned}
\end{equation} $
از آنجا که می دانیم این انرژی به دلیل اصطکاک از بین رفته است ، بنابراین باید به صورت گرما آزاد شود$ \begin{equation}
Q_{out}=-\Delta E >0
\end{equation}$
اگر اولین قانون ترمودینامیک را برای این سیستم بنویسیم و از این واقعیت استفاده کنیم که انرژی داخلی یک نوسان ساز هارمونیک $U=Nk_bT $ است ، به دست می آوریم$\begin{equation}
\begin{aligned}
dU&=\delta Q- \delta W \\ 0 &= \delta Q - F dx \\ \rightarrow \delta Q &=kx dx
\end{aligned}
\end{equation} $
جایی که من استفاده می کنم کار انجام شده توسط سیستم$\delta W = kxdx $ است. ادغام این ما$\begin{equation}
\begin{aligned}
Q&=k \int_{x_i}^{x_f}xdx \\ &=-\Delta E
\end{aligned}
\end{equation} $که با این پیش بینی موافق است که گرما باید برابر با تغییر انرژی باشد.روش دوم:
به جای استفاده از انرژی یک اسیلاتور هارمونیک حرارتی ، بیایید از انرژی مکانیکی بعلاوه چیزی که ممکن است به دما بستگی داشته باشد استفاده کنیم (که از آنجا که دما ثابت نیست مهم نیست):$\begin{equation}
dU=kx dx+CdT
\end{equation} $
و بیایید فکر کنیم که توده ها عوامل خارجی هستند که به فنر نیرویی وارد می کنند. سپس قانون اول شکل می گیرد$ \begin{equation}
\begin{aligned}
dU&=\delta Q - \delta W \\kx dx &= \delta Q + (m+M)g dx
\end{aligned}
\end{equation}$
در اینجا یک شک مهم مطرح می شود: اگر سیستم و محیط آن نیروهای نابرابری را انجام می دهند ، کدام یک را باید هنگام نوشتن اثر در نظر بگیریم؟ در روش اول من از نیرویی استفاده کردم که فنر انجام می دهد ، در اینجا من از نیرویی که توده ها انجام می دهند استفاده می کنم. اکنون می توانیم گرما را به دست بیاوریم$\begin{equation}
\begin{aligned}
Q&=\int \Big[kx-(m+M)g\Big] dx \\ &= -\frac{g^2M^2}{2k}
\end{aligned}
\end{equation} $
از یک طرف این معادله را دوست دارم زیرا وقتی حد M → 0 را می گیریم گرما مستقیم به صفر می رسد. همچنین ، من این روش را دوست دارم ، زیرا در قانون اول روشن است که اگر ما انبساط را به صورت تصادفی انجام دهیم (به این معنی که نیروی خارجی همیشه برابر با نیروی هوک است) ، هیچ تبادل گرمی وجود ندارد. با این حال ، من هنوز نمی بینم که چرا گرما باید کمتر از انرژی از دست رفته در انبساط باشد.خوب باید بگم به نظر من ، هر دو روش نادرست هستند . شکل قانون اول که باید برای جهان استفاده کنید (توده ها به علاوه محیط اطراف) شکل کلی تر است:
$\Delta E=\Delta U+\Delta(PE)+\Delta(EE)+\Delta(KE)=Q-W $جایی که ΔU تغییر در انرژی داخلی است (جرم ها به علاوه محیط اطراف) ، $\Delta (PE) $ تغییر در انرژی پتانسیل جرم ها است $ \Delta (EE)$تغییر در انرژی الاستیک ذخیره شده فنر و $ \Delta (KE)$ تغییر در انرژی جنبشی توده ها است. (جرم ها به علاوه محیط اطراف) منزوی است ، بنابراین این سیستم ترکیبی کار W نمی کند و هیچ گرمای Q دریافت نمی کند. و تغییر در انرژی جنبشی جرم ها صفر است. بنابراین معادله فوق به موارد زیر کاهش می یابد:
$\Delta U+\Delta(PE)+\Delta(EE)=0 $
تغییر در انرژی الاستیک ذخیره شده چشمه است
$ \Delta (EE)=\frac{1}{2}k(x_f^2-x_i^2)=\frac{g^2}{k}\left(mM+\frac{M^2}{2}\right)$تغییر در انرژی پتانسیل توده ها توسط$\Delta (PE)=-(M+m)g(x_f-x_i)=-\frac{g^2}{k}(M^2+Mm) $
بنابراین تغییر در انرژی درونی جهان بین حالتهای اولیه و نهایی آن توسط:$\Delta U=\frac{M^2g^2}{2k} $
اگر برای ایجاد همین تغییر در انرژی درونی جهان ، یک فرایند برگشت پذیر جایگزین می کردیم ، مجبور بودیم مقداری گرما (از برخی منبع نامشخص) برابر با ΔU به جهان منتقل کنیم. از آنجا که دما تقریباً بدون تغییر خواهد بود ، تغییر آنتروپی جهان نیز صورت می گیرد$ \Delta E=\frac{\Delta U}{T}=\frac{M^2g^2}{2kT}$ من یک روش جایگزین میدم $(M+m)g-kx-F_D=(M+m)\frac{d^2x}{dt^2} $
که در آن FD نیروی کشش هوا (میرایی) است که توسط محیط اطراف روی سیستم اعمال می شود. توجه داشته باشید که FD همیشه علامت مشابه سرعت رو به پایین توده ها دارد. اگر این معادله را در سرعت dx / dt ضرب کنیم ، و بین زمان برابر با صفر و زمان نامحدود ادغام شویم (وقتی جرم ها متوقف می شوند) ، به دست می آوریم$ -\Delta (PE)-\Delta (EE)-W_D=0$
بنابراین کارهایی که توسط محیط اطراف روی سیستم انجام می شود تا حرکت توده ها را کاهش دهد$ W_D=-\Delta (PE)-\Delta (EE)=-\frac{M^2g^2}{2k}$
بنابراین ، کار کشیدن هوا توسط سیستم در اطراف آن منهای این است:
$W=-W_D=\Delta (PE)+\Delta (EE)=\frac{M^2g^2}{2k}\tag{1} $اگر اکنون اولین قانون ترمودینامیک را در سیستم جرم فنر اعمال کنیم ، به دست می آوریم:$ \Delta U_{syst}+\Delta (PE)+\Delta (EE)=Q-W\tag{2}$
جایی که در اینجا $\Delta U_{syst} $ نشان دهنده تغییر در انرژی داخلی سیستم جرم فنر است (مانند توسعه قبلی که نشان دهنده تغییر انرژی داخلی. اگر Eqns را ترکیب کنیم. 1 و 2 ، اکنون به دست می آوریم:$\Delta U_{syst}=Q $
جایی که Q نشان دهنده مقدار ناچیزی از جریان گرما از محیط اطراف به سیستم است. این جریان گرما به طور معمول کم است زیرا هم سیستم و هم محیط پیرامون آن تغییر دمای تعادلی یکسان را تجربه می کنند ، و جرم چند برابر ظرفیت گرمایی سیستم معمولاً بسیار کوچکتر از جرم برابر ظرفیت گرمایی محیط است.اگر اکنون اولین قانون ترمودینامیک را در محیط پیرامون خود اعمال کنیم ، به دست می آوریم:
$\Delta U_{surr}=-Q-W_D=-Q+\frac{M^2g^2}{2k} $بنابراین تغییر انرژی درونی کل است $\Delta U=\Delta U_{syst}+\Delta U_{surr}=\frac{M^2g^2}{2k} $
ΔU = ΔUsyst + ΔUsurr = M2g22k
هنگامی که یک ماده کاملاً الاستیک تغییر شکل می یابد ، انرژی مرتبط با فشار به عنوان انرژی پتانسیل الاستیک در بدن ذخیره می شود ، به آن انرژی کرنش گفته می شود. با از بین بردن نیروهای تغییر شکل دهنده ، بدن کاملاً شکل ، اندازه و پیکربندی اصلی خود را از دست می دهد و دیگر از بین رفتن گرما نیست. با این حال ، هیچ چیز کاملاً الاستیک نیست! هنگامی که یک ماده جزئی الاستیک (به عنوان مثال ، یک نوار لاستیکی) تغییر شکل می یابد ، حتی در صورت خارج شدن نیروهای تغییر شکل دهنده ، همیشه یک تغییر شکل باقی مانده وجود دارد. پسماند و بخشی از انرژی تبدیل شده به گرما را نشان می دهد. در اینجا یک مرجع سریع است.این تغییر شکل باقیمانده چگونه مسئول گرم شدن مواد است؟$dT=\frac{T}{C_V}\Big[dS-\Big(\frac{\partial P}{\partial T}\Big)_V dV\Big], $
ما توجه داریم که تغییر دما به دلیل تغییر در حجم V یا تغییر در آنتروپی S یا هر دو ایجاد می شود. آیا می توانیم با استفاده از این موضوع بفهمیم چه خبر است؟
حدس من این است که برای تغییر شکل الاستیک یک ماده کاملاً الاستیک ، در طول فرآیند بارگیری dT منفی است زیرا dV> 0 و در هنگام تخلیه dT مثبت است زیرا dV <0. در کل چرخه ، وقتی سیستم به حالت اولیه خود می رسد ، گرم نمی شودیک ماده الاستیک تا حدودی (به عنوان مثال ، ماده ویسکوالاستیک) ترکیبی از رفتار الاستیک و چسبناک را نشان می دهد ، و این قسمت چسبناک است که مسئول افزایش انرژی داخلی (مورد آدیاباتیک) یا انتشار گرما است (مورد همدما).
یک فنر و یک دمپر (داشپات) را بصورت سریالی تصور کنید. هنگامی که ترکیب کشیده می شود ، فنر و دمپر هر دو گسترش می یابند ، اما امتداد دمپر مسئول اتلاف انرژی مکانیکی به هر دو انرژی داخلی گرما است. بنابراین ، هنگامی که نیروی گسترش دهنده ترکیب آزاد می شود ، فنر می تواند به طول اصلی خود بازگردد ، اما طول جدید دمپر قفل می شود. بنابراین ترکیب کلی برخی از پسوندهای باقیمانده را حفظ می کند ، و مقداری از انرژی مکانیکی توسط دمپر
و ما P را به عنوان فشار و ... را به عنوان انرژی درونی یک ماده جامد تعریف می کنیم. اینها را می توان به دو قسمت تقسیم کرد: یک قسمت الاستیک و یک قسمت حرارتی. $P_{c} $ و $ \epsilon_{c}$ فقط به چگالی ماده ، ρ یا حجم خاص ، $V = 1 / ρ$ بستگی دارد. اینها برابر با فشار کل و انرژی داخلی خاص در صفر مطلق یا T = 0 K هستند. فرض کنیم که حجم ویژه در T = 0 و P = 0 توسط Voc داده شود ، که فقط ~ 1-2٪ کوچکتر از حجم ویژه در STP ، Vo ، برای بیشتر فلزات.
منحنی انرژی پتانسیل یا منحنی تعریف کننده ϵc ، از نظر کیفی شبیه منحنی انرژی پتانسیل است که تعامل بین دو اتم را به عنوان تابعی از فاصله هسته ای ، Δxn توصیف می کند. وقتی V> Voc ، نیروهای جذاب غالب می شوند اما با افزایش فواصل درون هسته ای به سرعت سقوط می کنند (به عنوان مثال ، با افزایش T). به عبارت دیگر ، وقتی اتمها از هم دورتر شوند ، asc به طور مجانبی تا مقداری مقدار U افزایش می یابد ، که تقریباً انرژی اتصال اتمها در بدن است. بنابراین ، U انرژی مورد نیاز برای حذف همه اتمها از جسم تا بی نهایت را نشان می دهد ، که تقریباً برابر با گرمای تبخیر ماده است ... بنابراین ، ϵc (V) → U به عنوان $ \Delta x_{n} \rightarrow \sim 2$.
برعکس ، اگر نیروهای V <Voc باشد نیروهای دافعه مسلط می شوند. با در نظر گرفتن این که کار انجام شده با فشرده سازی مواد برابر با افزایش در خواهد بود ، می توانیم این مقدار را کمی تعریف کنیم$P_{c} = - \left( \frac{ d \epsilon_{c} }{ d V } \right)_{T = 0} $
اگر از اولین هویت ترمودینامیکی بالا استفاده کنیم ، دو نتیجه خواهیم یافت ، یکی برای پارامترهای الاستیک و دیگری برای حرارتی:
$\begin{align}
\left( \frac{ \partial \epsilon_{c} }{ \partial V } \right)_{T} & = \frac{ d \epsilon_{c} }{ d V } = - P_{c}\left( V \right) \tag{2a} \\
\left( \frac{ \partial \epsilon_{T} }{ \partial V } \right)_{T} & = 0 = T \left( \frac{ \partial P_{T} }{ \partial T } \right)_{V} - P_{T} \tag{2b}
\end{align} $
من شکل خطی اونو که ساده هست بیان میکنم ترمودینامیک یک فنر منفرد در پتانسیل جاذبه
من سعی می کنم این مشکل ترمودینامیک را حل کنم. یک چشمه ثابت k الاستیک وجود دارد که در موقعیت تعادل آن به جرم m متصل است $\begin{equation}
x_{0}=\frac{mg}{k}
\end{equation} $
ناگهان در انتهای فنر جرم جدید M اضافه می کنیم بنابراین فنر برای مدتی نوسان می کند تا اینکه در موقعیت تعادل جدیدی قرار بگیرد. این در دمای ثابت T و در تماس با دمای هوا اتفاق می افتد$\begin{equation}
x_f=\frac{(m+M)g}{k}
\end{equation} $سوال من این است: در طی آن فرایند چقدر گرما آزاد یا جذب فنر می شود و میزان آنتروپی جهان چقدر افزایش می یابد؟
مشکل من این است که من دو روش جایگزین برای این کار دارم و آنها دو نتیجه می دهند. علاوه بر این ، ظرایف خاصی از ترمودینامیک وجود دارد که مرا گیج می کند. بگذارید دو روش را توضیح دهم:انرژی که سیستم از دست داده است برابر است با:$\begin{equation}
\begin{aligned}
\Delta E &= E_f-E_i \\ &= -\frac{g^2(m+M)^2}{k}+\frac{g^2m^2}{k}
\end{aligned}
\end{equation} $
از آنجا که می دانیم این انرژی به دلیل اصطکاک از بین رفته است ، بنابراین باید به صورت گرما آزاد شود$ \begin{equation}
Q_{out}=-\Delta E >0
\end{equation}$
اگر اولین قانون ترمودینامیک را برای این سیستم بنویسیم و از این واقعیت استفاده کنیم که انرژی داخلی یک نوسان ساز هارمونیک $U=Nk_bT $ است ، به دست می آوریم$\begin{equation}
\begin{aligned}
dU&=\delta Q- \delta W \\ 0 &= \delta Q - F dx \\ \rightarrow \delta Q &=kx dx
\end{aligned}
\end{equation} $
جایی که من استفاده می کنم کار انجام شده توسط سیستم$\delta W = kxdx $ است. ادغام این ما$\begin{equation}
\begin{aligned}
Q&=k \int_{x_i}^{x_f}xdx \\ &=-\Delta E
\end{aligned}
\end{equation} $که با این پیش بینی موافق است که گرما باید برابر با تغییر انرژی باشد.روش دوم:
به جای استفاده از انرژی یک اسیلاتور هارمونیک حرارتی ، بیایید از انرژی مکانیکی بعلاوه چیزی که ممکن است به دما بستگی داشته باشد استفاده کنیم (که از آنجا که دما ثابت نیست مهم نیست):$\begin{equation}
dU=kx dx+CdT
\end{equation} $
و بیایید فکر کنیم که توده ها عوامل خارجی هستند که به فنر نیرویی وارد می کنند. سپس قانون اول شکل می گیرد$ \begin{equation}
\begin{aligned}
dU&=\delta Q - \delta W \\kx dx &= \delta Q + (m+M)g dx
\end{aligned}
\end{equation}$
در اینجا یک شک مهم مطرح می شود: اگر سیستم و محیط آن نیروهای نابرابری را انجام می دهند ، کدام یک را باید هنگام نوشتن اثر در نظر بگیریم؟ در روش اول من از نیرویی استفاده کردم که فنر انجام می دهد ، در اینجا من از نیرویی که توده ها انجام می دهند استفاده می کنم. اکنون می توانیم گرما را به دست بیاوریم$\begin{equation}
\begin{aligned}
Q&=\int \Big[kx-(m+M)g\Big] dx \\ &= -\frac{g^2M^2}{2k}
\end{aligned}
\end{equation} $
از یک طرف این معادله را دوست دارم زیرا وقتی حد M → 0 را می گیریم گرما مستقیم به صفر می رسد. همچنین ، من این روش را دوست دارم ، زیرا در قانون اول روشن است که اگر ما انبساط را به صورت تصادفی انجام دهیم (به این معنی که نیروی خارجی همیشه برابر با نیروی هوک است) ، هیچ تبادل گرمی وجود ندارد. با این حال ، من هنوز نمی بینم که چرا گرما باید کمتر از انرژی از دست رفته در انبساط باشد.خوب باید بگم به نظر من ، هر دو روش نادرست هستند . شکل قانون اول که باید برای جهان استفاده کنید (توده ها به علاوه محیط اطراف) شکل کلی تر است:
$\Delta E=\Delta U+\Delta(PE)+\Delta(EE)+\Delta(KE)=Q-W $جایی که ΔU تغییر در انرژی داخلی است (جرم ها به علاوه محیط اطراف) ، $\Delta (PE) $ تغییر در انرژی پتانسیل جرم ها است $ \Delta (EE)$تغییر در انرژی الاستیک ذخیره شده فنر و $ \Delta (KE)$ تغییر در انرژی جنبشی توده ها است. (جرم ها به علاوه محیط اطراف) منزوی است ، بنابراین این سیستم ترکیبی کار W نمی کند و هیچ گرمای Q دریافت نمی کند. و تغییر در انرژی جنبشی جرم ها صفر است. بنابراین معادله فوق به موارد زیر کاهش می یابد:
$\Delta U+\Delta(PE)+\Delta(EE)=0 $
تغییر در انرژی الاستیک ذخیره شده چشمه است
$ \Delta (EE)=\frac{1}{2}k(x_f^2-x_i^2)=\frac{g^2}{k}\left(mM+\frac{M^2}{2}\right)$تغییر در انرژی پتانسیل توده ها توسط$\Delta (PE)=-(M+m)g(x_f-x_i)=-\frac{g^2}{k}(M^2+Mm) $
بنابراین تغییر در انرژی درونی جهان بین حالتهای اولیه و نهایی آن توسط:$\Delta U=\frac{M^2g^2}{2k} $
اگر برای ایجاد همین تغییر در انرژی درونی جهان ، یک فرایند برگشت پذیر جایگزین می کردیم ، مجبور بودیم مقداری گرما (از برخی منبع نامشخص) برابر با ΔU به جهان منتقل کنیم. از آنجا که دما تقریباً بدون تغییر خواهد بود ، تغییر آنتروپی جهان نیز صورت می گیرد$ \Delta E=\frac{\Delta U}{T}=\frac{M^2g^2}{2kT}$ من یک روش جایگزین میدم $(M+m)g-kx-F_D=(M+m)\frac{d^2x}{dt^2} $
که در آن FD نیروی کشش هوا (میرایی) است که توسط محیط اطراف روی سیستم اعمال می شود. توجه داشته باشید که FD همیشه علامت مشابه سرعت رو به پایین توده ها دارد. اگر این معادله را در سرعت dx / dt ضرب کنیم ، و بین زمان برابر با صفر و زمان نامحدود ادغام شویم (وقتی جرم ها متوقف می شوند) ، به دست می آوریم$ -\Delta (PE)-\Delta (EE)-W_D=0$
بنابراین کارهایی که توسط محیط اطراف روی سیستم انجام می شود تا حرکت توده ها را کاهش دهد$ W_D=-\Delta (PE)-\Delta (EE)=-\frac{M^2g^2}{2k}$
بنابراین ، کار کشیدن هوا توسط سیستم در اطراف آن منهای این است:
$W=-W_D=\Delta (PE)+\Delta (EE)=\frac{M^2g^2}{2k}\tag{1} $اگر اکنون اولین قانون ترمودینامیک را در سیستم جرم فنر اعمال کنیم ، به دست می آوریم:$ \Delta U_{syst}+\Delta (PE)+\Delta (EE)=Q-W\tag{2}$
جایی که در اینجا $\Delta U_{syst} $ نشان دهنده تغییر در انرژی داخلی سیستم جرم فنر است (مانند توسعه قبلی که نشان دهنده تغییر انرژی داخلی. اگر Eqns را ترکیب کنیم. 1 و 2 ، اکنون به دست می آوریم:$\Delta U_{syst}=Q $
جایی که Q نشان دهنده مقدار ناچیزی از جریان گرما از محیط اطراف به سیستم است. این جریان گرما به طور معمول کم است زیرا هم سیستم و هم محیط پیرامون آن تغییر دمای تعادلی یکسان را تجربه می کنند ، و جرم چند برابر ظرفیت گرمایی سیستم معمولاً بسیار کوچکتر از جرم برابر ظرفیت گرمایی محیط است.اگر اکنون اولین قانون ترمودینامیک را در محیط پیرامون خود اعمال کنیم ، به دست می آوریم:
$\Delta U_{surr}=-Q-W_D=-Q+\frac{M^2g^2}{2k} $بنابراین تغییر انرژی درونی کل است $\Delta U=\Delta U_{syst}+\Delta U_{surr}=\frac{M^2g^2}{2k} $
ΔU = ΔUsyst + ΔUsurr = M2g22k

- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: هوافضا
چرا برخی از پنجرههای کابین خلبان قابل باز شدن هستند؟چرا هواپیما اجازه می دهد پنجره های کشویی در کابین خلبان باز شود؟ چه هدفی را دنبال می کند و چرا نمی توان همین کار را برای پنجره های سرنشین نیز انجام داد؟پنجرههای باز شدن کابین خلبان برخی از اهداف را انجام میدهند، مانند فراهم کردن وسیله اضافی برای تخلیه در مواقع اضطراری.
اهداف دیگری مانند کمک به بازرسی خدمه، سیگنال دادن به خدمه زمینی، تهویه اضافی، خروج دود و غیره وجود دارد (همچنین می توان از آن برای پرتاب اشیا به بیرون استفاده کرد، اگرچه به طور کلی توصیه نمی شود). به نظر می رسد یکی از دلایل اصلی (حداقل در گذشته) بهبود دید خلبان در مواردی که شیشه جلو مات می شود، باشد.
پنجره ها در همه هواپیماها یافت نمی شوند (مثلاً 787 آن را ندارد) و باز کردن آن خیلی آسان نیست (توجه داشته باشید که به سمت داخل باز می شود).
ابتدا یک مکانیسم قفل وجود دارد، سپس یک میل لنگ که کل مجموعه پنجره از جمله قاب را حرکت می دهد، یا یک اهرم برای حرکت مجموعه پنجره. هنگامی که پنجره بسته و قفل است، بسته می شود. وقتی باز است، مانند پنجره ماشین شما از قاب جدا نمی شود.
(ب) شرایط بارندگی. برای شرایط بارندگی موارد زیر اعمال می شود:
(1) هواپیما باید وسیله ای برای حفظ قسمتی از شیشه جلو در شرایط بارندگی داشته باشد، به طوری که هر دو خلبان بتوانند دید وسیعی در طول مسیر پرواز در حالت پرواز عادی هواپیما داشته باشند.
(3) اولین خلبان باید پنجره ای داشته باشد که-
(i) در شرایطی که کابین تحت فشار نباشد تحت شرایط مقرر در بند (ب) (1) این بخش قابل باز شدن است.
(4) پنجره قابل باز شدن مشخص شده در بند (ب) (3) این بخش نیازی به ارائه ندارد اگر نشان داده شود که سطحی از سطح شفاف به اندازه کافی برای حداقل یک خلبان برای فرود ایمن هواپیما در این صورت شفاف باقی می ماند. از-
(ii) برخورد با تگرگ شدید، پرندگان یا حشرات.
در یک کابین تحت فشار، تهیه پنجره ایده خوبی نیست. (علاوه بر افزایش وزن)، اگر کسی بتواند پنجره را باز کند، دستوری برای فاجعه خواهد بود (کاهش فشار -> ماسک های اکسیژن -> زمین).
*بسیاری از هواپیماها دارای طناب های فرار هستند که در یک محفظه بالای پنجره در هر طرف کابین خلبان نصب شده اند، مانند کابین خلبان A320
آیا استفاده از انرژی باد در هواپیما معقول است؟در واقع ایده ساخت یک هواپیمای الکتریکی است که انرژی آن از خورشید و باد در هنگام فرود هواپیما تامین شود. به جای استفاده از اسپویلر به عنوان ترمز هوا، این توربینهای بادی که به طور جداگانه نصب میشوند، میتوانند انرژی دراگ و مهار را به طور همزمان اضافه کنند. به عبارت دیگر ترمز احیا کننده.به طور معمول خیر: استخراج انرژی از جریان هوا باعث ایجاد نیروی پسا می شود که باید با رانش اضافه بر آن غلبه کرد. از آنجایی که هر شکلی از تبدیل انرژی باعث تلفات می شود، باید انرژی رانش بیشتری نسبت به جریان هوا اضافه شود.
تنها زمانی که موتورها از کار بیفتند و ژنراتورها از کار بیفتند، استخراج انرژی از جریان هوا منطقی است. در هواپیما دو کاربرد وجود دارد که توسط "انرژی باد" هدایت می شود:
هواپیماهای قدیمیتر از ژیروسها برای افق مصنوعی استفاده میکنند که توسط هوای قوچ تغذیه میشوند. به این ترتیب ژیروسکوپ ها حتی پس از خرابی موتور نیز کار می کنند.
جتها از توربینهای هوایی Ram (RAT) استفاده میکنند، ژنراتورهای پروانهای که در زمانی که سایر ابزارهای تولید برق و نیروی هیدرولیک از کار افتاده باشند، به جریان هوا منتقل میشوند. توجه داشته باشید که این کار در پرواز بدون نیرو انجام می شود و میزان فرورفتگی را افزایش می دهد. با تمرکز جدید سوال شما بر نیروی محرکه الکتریکی، پاسخ متفاوت خواهد بود. اکنون به احتمال زیاد ملخ هایی خواهید داشت که با موتورهای الکتریکی کار می کنند. در هنگام فرود، آنها می توانند معکوس عمل کنند و باتری را شارژ کنند، که به احتمال زیاد تا زمان فرود هواپیما خالی می شود. این را می توان در طول نزدیک شدن نهایی تا پایان ران اوت پس از تاچ داون انجام داد. می توان انتظار داشت که هر هواپیمای برقی دارای L/D بالایی باشد، بنابراین استفاده از ترمزهای سرعت برای ایجاد یک رویکرد تندتر منطقی است.
با این حال، اگر یک دستگاه اضافی مقرون به صرفه باشد، تعجب می کنم. این شارژ مجدد باید توسط سیستم پیشرانه معمولی انجام شود، در غیر این صورت در بیشتر طول پرواز به وزن مرده اضافه می شود.
شما فرمولها را درخواست کردید، اما تنها چیزی که میتوانم در اینجا ارائه کنم، محاسبات پشت پاکت است. ابتدا باید گفت که ملخهای گام متغیر مانند آسیابهای بادی سست خواهند بود، زیرا پیچ و خم آنها برای حالت آسیاب بادی اشتباه است. من انتظار دارم که راندمان آنها حدود 30٪ باشد، به این معنی که تنها 30٪ از انرژی استخراج شده توسط درگ به انرژی مکانیکی تبدیل می شود که موتور الکتریکی را به حرکت در می آورد.
در مرحله بعد، راه اندازی یک موتور الکتریکی به عنوان یک ژنراتور مجدداً مستلزم مصالحه است. موتورهای خوب ژنراتورهای ضعیفی را ایجاد می کنند و سیم کشی مجدد موتور برای عملکرد بهتر ژنراتور باعث کاهش کارایی آن در استفاده معمولی می شود. وقتی موتور معکوس منطقی به نظر می رسد، به سرعت بیش از آنچه در مرحله پرواز کوتاه به دست می آورید، ضرر خواهید کرد.حال بیایید فرض کنیم که شما سیستم پیشرانه خود را در بالاترین بازده (مثلاً 90%) نگه دارید و بپذیرید که تنها 10٪ از انرژی دراگ را به انرژی الکتریکی تبدیل می کند. اجازه دهید همچنین فرض کنیم که هواپیمای خورشیدی آینده شما دارای L/D 30 است که برای یک رویکرد عملی باید به 10 کاهش یابد. شما این کار را از 1000 فوت به پایین انجام میدهید و از پروانه آسیاب بادی نیز در هنگام خروج استفاده میکنید. سرعت تقریب v، جرم m و انرژی اولیه هواپیما$305\cdot m\cdot 9.81 + \frac{m}{2} \cdot v^2$ است. دو سوم انرژی پتانسیل وارد کشش پروانه می شود، و برای اینکه سخاوتمندانه باشیم، فرض می کنیم که 100٪ انرژی جنبشی نیز به کشش پروانه می رود، حتی اگر نیروی ترمز پروانه ها در سرعت پایین واقعا ضعیف است و نیاز به پشتیبانی از چرخ دارد. ترمزها
اکنون مهم است که هواپیمای شما با چه سرعتی پرواز می کند، زیرا این امر باعث تغییر نسبت بین انرژی پتانسیل و انرژی جنبشی می شود. برای ساده نگه داشتن همه چیز، من هر دو را با انرژی مورد نیاز برای پرواز بعدی مرتبط خواهم کرد. 10٪ از انرژی جنبشی کامل هواپیما را به کمتر از یک سوم سرعت پرواز شتاب می دهد - پس از این، 91٪ انرژی باقی مانده برای رسیدن به v باید با شارژ باتری ها در بین پروازها اضافه شود.
انرژی الکتریکی گرفته شده از انرژی پتانسیل به شما کمک می کند تا ارتفاع 60 فوتی بالا بروید یا پرواز در سطح v را برای مسافت 1800 فوت حفظ کنید. در L/D 30 هواپیما مسافت 30000 فوتی را بدون رانش پرواز می کند و با ترمز کردن شما انرژی را برای پوشش 20000 فوت استخراج می کنید که با راندمان تبدیل 10% (و 90% راندمان نیروی محرکه!) شما را با خود می برد. فقط 1800 فوت
اجازه دهید ابتدا روی فرود از ارتفاع کروز تا نزدیک شدن نهایی تمرکز کنیم. در حالت ایدهآل، این فرود با موتورهایی انجام میشود که در پایینترین حالت رانش (بیکار پروازی) قرار دارند، به این معنی که موتورها نیرو را برای سیستمهای مختلف الکتریکی و هیدرولیک، و فشار، و کمی رانش فراهم میکنند، زیرا واقعاً نمیتوانید از آن اجتناب کنید. روی یک جت از نظر تئوری، این می تواند توسط یک توربین هوایی Ram انجام شود (حالا فرض کنیم که هواپیمای فرضی ما مجهز به نسخه نسبتاً بزرگی است که به راحتی تمام سیستم های فوق الذکر را تغذیه می کند، زیرا یک RAT معمولی فقط می تواند قدرت اضطراری محدودی را ارائه دهد). با این حال، این کشش را تا حد زیادی افزایش می دهد و برای حفظ سرعت، مشخصات فرود تندتر خواهد بود. این به نوبه خود به این معنی است که هواپیما باید زمان بیشتری را در ارتفاع کروز بگذراند، که برای نگهداری آن نیاز به انرژی دارد.
راه دیگری برای بررسی این موضوع، یک تراز انرژی ساده است: مقدار محدودی از انرژی پتانسیل وجود دارد، و واقعاً مهم نیست که از آن فقط برای حفظ سرعت استفاده میکنید یا از آن برای حفظ سرعت و ترمز احیاکننده استفاده میکنید. ، زیرا مقدار کل انرژی که می توانید از آن استخراج کنید همیشه یکسان است.
البته یک لحظه وجود دارد که هواپیماها باید ترمز کنند و آن بعد از تاچ داون است. بیایید فعلاً فرض کنیم که از محیط زیست بسیار آگاه هستیم و از هیچ وسیله دیگری برای ترمز به جز سیستم ترمز احیا کننده استفاده نمی کنیم. هواپیما هنوز با سرعتی در حدود 130 کیلو در ساعت، 240 کیلومتر در ساعت یا 150 مایل در ساعت حرکت می کند، بنابراین مطمئناً این به ما انرژی زیادی می دهد؟ بیایید برای تعدادی از ارقامی که برای یک بوئینگ 737-300 پیدا کردم، یک محاسبه پشت پاکت انجام دهیم.
فرض کنید با وزن 60000 کیلوگرم (نزدیک به MLW) با فلپ های کاهش یافته به 15 فرود می آییم، که سرعت فرود 158kts=81.3m/s را به ما می دهد. مقدار انرژی جنبشی 12mv2≈200MJ است (بله، این مگا ژول است!). این خیلی انرژی است، نه؟! خوب... نه واقعا. نفت سفید (که تقریباً مشابه سوخت جت است) با چگالی انرژی در حدود 46 مگا ژول بر کیلوگرم تولید می شود. ما در مورد چیزی معادل کمی بیش از 4 کیلوگرم نفت سفید صحبت می کنیم، در هواپیمایی که حدود 16000 کیلوگرم از آن را حمل می کند. این بدان معناست که ما حدود 0.025 درصد از ظرفیت سوخت را بازسازی می کنیم.
من آن را به عنوان تمرینی به خواننده می سپارم تا فکر کند که آیا می توان یک سیستم ترمز احیا کننده طراحی کرد، به طوری که سوخت اضافی مورد استفاده به دلیل وزن و اندازه آن کمتر از 0.025٪ باشد.
بیایید محاسبه را روی هواپیمایی انجام دهیم که در واقع بیشتر تجهیزات لازم (باتری ها و موتورهای الکتریکی که احتمالاً می توانند به عنوان دینام یا دینام عمل کنند) را در هواپیما دارد: Solar Impulse 2. ظرفیت باتری فوق العاده 4x41kWh (590MJ) دارد. با فرض یکسان بودن سرعت برخاستن و فرود (20kts=36km/h=10m/s) و با وزن بارگذاری شده 2300 کیلوگرم، انرژی جنبشی هنگام فرود 115 کیلوژول است. این 0.0195 درصد ظرفیت باتری است - تقریباً مشابه نمونه B733 ما! و توجه داشته باشید که این دوباره با فرض بازیابی 100% انرژی جنبشی پروانه ها است... این ایده هرگز عملی نخواهد شد. (برای مقایسه، کمتر از دو ثانیه انرژی تولید شده توسط پنل های خورشیدی در اوج رتبه مربوطه است)توربین های بادی روی زمین می ایستند و توده هوا با سرعتی از آنها عبور می کند، بنابراین انرژی جنبشی دارد. اما هواپیما نسبت به باد در حال حرکت است، بنابراین باد قاب استراحت است و انرژی ندارد. بنابراین وقتی هواپیما از جریان هوا و/یا فشار هوا استفاده می کند، از انرژی خود استفاده می کند نه باد¹.
البته اکنون توربین نصب شده روی هواپیما انرژی تولید می کند. اما این به هزینه انرژی هواپیما خواهد بود. هنگام پرواز در سطح زیر قدرت، نیرو از موتورها می آید، بنابراین استخراج مستقیم آن از طریق ژنراتور نصب شده روی درایو جانبی کارآمدتر است. اما حتی زمانی که هواپیما در حالت بیکار فرود میآید، انرژی بالقوه آن هزینه میشود و این انرژی در ابتدا توسط موتورها در هنگام صعود تامین میشد. خاموش کردن زودتر موتور و استفاده از تمام آن برای جبران درگ در هنگام سر خوردن کارآمدتر است.
این در مورد موتور گلایدر خورشیدی مانند هر هواپیمای دیگری صدق می کند. توقف زودتر موتورها و سر خوردن در حول و حوش بهترین زاویه لغزش کارآمدتر از کارکردن بیشتر موتورها و سپس تولید مجدد انرژی است، زیرا نه تبدیل انرژی الکتریکی به انرژی پتانسیل از طریق موتور و پروانه و نه تبدیل از انرژی پتانسیل به انرژی الکتریکی از طریق توربین و ژنراتور بسیار کارآمد است.
و حتی در هنگام استفاده از مواد حرارتی یا دیگر هوای افزایش دهنده برای به دست آوردن انرژی بالقوه نیز کاربرد دارد. دوباره کارآمدتر است که از تبدیل انرژی اجتناب کنید و به سادگی از حرارت برای به دست آوردن ارتفاع استفاده کنید و در حالی که انرژی الکتریکی را مستقیماً از پانل های خورشیدی دریافت می کنید، لغزش را افزایش دهید.
همچنین وزن عامل محدود کننده مهم برای موتور گلایدر خورشیدی خواهد بود. این بدان معناست که شما نمیتوانید باتریهای زیادی را سوار کنید و به نوبه خود به این معنی است که ترمز احیاکننده چندان مفید نخواهد بود زیرا ظرفیت زیادی برای ذخیره انرژی ندارید. همچنین به این معنی است که ممکن است بخواهید از توربین اختصاصی برای کاهش وزن خودداری کنید. شما همچنان قادر خواهید بود مقداری انرژی را از پروانه های آسیاب بادی با راندمان کمتری دوباره تولید کنید. اما همانطور که توضیح داده شد، آنقدرها هم منطقی نیست.
تنها زمانی که هواپیما از توربین استفاده می کند در شرایط اضطراری است. هنگامی که همه موتورها از کار می افتند، از توربین هوای رم برای تامین انرژی سیستم های الکتریکی و هیدرولیک ضروری استفاده می شود. مسافت سر خوردن را کمی کوتاه می کند، اما اگر منبع تغذیه دیگری در دسترس نباشد ارزشش را دارد.
تا آنجایی که باد پیش می رود، تنها کاربرد عملی باد، انتخاب مسیر است که تا حد امکان باد دنباله دار در طول سفر دریایی وجود داشته باشد. برای مثال مسیرهای اقیانوس اطلس شمالی به طور دوره ای تنظیم می شوند تا به پروازهای شرق اجازه استفاده از جت استریم را بدهد. به یک معنا، این از انرژی باد استفاده می کند، زیرا هواپیما برای رسیدن به مقصد سوخت کمتری می سوزاند.
¹ انرژی کمیت عجیبی است. در تمام قاب های مرجع اینرسی حفظ می شود، اما برخی از اشکال آن در هر یک مقادیر متفاوتی خواهند داشت. شما می توانید یک چارچوب مرجع را انتخاب کنید که در آن باد انرژی داشته باشد، اما منطقی تر خواهد بود.
آیا حداکثر اندازه ممکن برای یک هواپیما وجود دارد؟
تصادفی نیست که بزرگترین پرندگان پرواز نمی کنند. توانایی پرواز با افزایش اندازه کاهش می یابد، بنابراین محدودیت بالایی برای هواپیما نیز وجود دارد. دلیل اصلی این است که با افزایش اندازه، تودهها با افزایش اندازه مکعب بالا میروند در حالی که ساختارهای باربر مانند سطح مقطع بال اسپار تنها با افزایش مربع اندازه رشد میکنند. این قانون قدرت ساده ترین قوانین مقیاس بندی است.
از آنجایی که بارهای روی بال هواپیما نه تنها به اندازه آن، بلکه به بسیاری از پارامترهای دیگر (زاویه حمله، سرعت، نسبت ابعاد ...) بستگی دارد، هیچ مرز مشخصی وجود ندارد و پیشرفت در مواد کمک می کند تا محدودیت اندازه را تغییر دهد. اگر کسی بخواهد بزرگترین هواپیمای دنیا را بسازد، طول بالها به راحتی میتواند دو برابر اندازه بزرگترین هواپیماهای امروزی باشد، اما کاربرد این هواپیما بسیار محدود خواهد بود.
استفاده از این هواپیما برای سفر مسافران محدودیتهای بیشتری مانند تعداد خروجیهای اضطراری و حداکثر فاصله تا نزدیکترین خروجی را اضافه میکند، اما با استفاده از چندین بدنه کوچکتر میتوان بر این مسئله غلبه کرد. یک هواپیمای دو بدنه نیز وزن محموله را پخش می کند، بنابراین بال خمش ریشه کاهش می یابد.
بلافاصله محدودیت اندازه را به میزان قابل توجهی افزایش می دهد. با این حال، برای برخاستن از آن به باندهای جدید و عریضتری نیاز دارد. و افزودن بدنه بیشتر به همان بال به زودی با مشکلات بال زدن مواجه خواهد شد.
نشانه بعدی می تواند طرح هایی باشد که مورد مطالعه قرار گرفته و امکان پذیر بوده است اما در نهایت به دلایل اقتصادی ساخته نشده اند. در اینجا بزرگترین وسایل نقلیه اثر زمینی هستند: پرواز آهسته در هوای متراکم محدودیت اندازه را بالا می برد. بوئینگ پلیکان با طول بال 152 متر برنامه ریزی شده بود و بریف بال را با 2500 تن جرم برخاستن و 125.5 متر طول بال پیشنهاد کرد.
من حدس میزنم که طول بالهای 200 متری هنوز امکانپذیر است، و هنگام پخش وزن حتی 500 متر باید واقعبینانه باشد،
بله، حد بالایی وجود دارد، اما این حد بالا ممکن است با نوآوری های تکنولوژیکی تغییر کند.
یک هواپیما به دلیل ضریب بالابر $L=\frac12\rho v^2 A C_L$ پرواز می کند، با v سرعت هوا، که ترکیبی از سرعت هواپیما و سرعت باد است، ρ≈1kg m-3 در حداقل نظری ارتفاع 5 کیلومتر (به یاد داشته باشید که بیشتر هواپیماها به 10 کیلومتر می رسند، اما من برای نشان دادن حد بالایی)، A مساحت، و CL یک ضریب با مقدار معمولی کمتر از 2، که ممکن است با نوآوری های تکنولوژیکی تغییر کند، کمی افراطی تر در نظر گرفتم.
بنابراین تنها عواملی که میتوانیم بر آنها تأثیر بگذاریم v و A هستند. با این حال، اگر A را افزایش دهیم، جرم m سریعتر از ناحیه A افزایش مییابد زیرا برای جلوگیری از شکستن شکل صفحه تحت نیروهای عظیم، مواد بیشتری مورد نیاز است. افزایش درجه دوم A بیش از یک درجه دوم بر حسب m می دهد و بنابراین در L مورد نیاز.
اگر v را افزایش دهیم به سوخت بیشتری نیاز داریم. مقدار سوخت در واحد مسافت به صورت خطی در v افزایش می یابد، زیرا به صورت درجه دوم در واحد زمان در v افزایش می یابد. بنابراین L به صورت درجه دوم افزایش می یابد که m فقط به صورت خطی افزایش می یابد. این بدان معنی است که ما ممکن است با افزایش v کاری انجام دهیم. این بدان معناست که هواپیماها باید قبل از بلند شدن سریعتر حرکت کنند، که به خطوط بلندتری نیاز دارد. توجه داشته باشید که ما نمی توانیم به افزایش v ادامه دهیم زیرا نمی توانیم کنترل خود را از دست بدهیم.
به طور خلاصه، چیزهایی که ما می توانیم بهبود دهیم عبارتند از v، سرعت، CL، با نوآوری های تکنولوژیکی و ρ با کاهش ارتفاع پرواز. با این حال، عملی نیست.هیچ باندی وجود ندارد که بتواند چنین هواپیمایی را تحمل کند. هواپیماهایی مانند A380 و 747 در حال حاضر به دلیل ظرفیت طول/وزن باند مسیر محدود شدهاند. شما باید باندهای فرودگاه را تغییر دهید تا هر چیزی به طور قابل توجهی بزرگتر انجام شود. البته با این فرض که به روشی مشابه بیشتر هواپیماهای مسافربری فرود می آید (یعنی نه VTOL)
چه مسیری قرار است پرواز کند؟ اندازه هواپیماها به این دلیل نیست که نمیتوانیم آنها را بزرگتر بسازیم، آنها به اندازه آنها هستند زیرا مسیرها به آنها دیکته میکنند که این اندازه باشند. آیا واقعاً نیاز دارید که 1000 نفر را در یک مسیر معین به طور همزمان جابجا کنید؟ چند مسیر اینقدر تراکم سفر دارند؟
بیایید به صورت فرضی به این موضوع نگاه کنیم، Jamiec به نکته بسیار خوبی اشاره میکند که هواپیمای دارای ظرفیت بیش از 7 میلیارد بیفایده است، بنابراین بیایید آن را حداکثر در نظر بگیریم. اگر XKCD در یک سوال مشابه این موضوع را پوشش دهد و تخمین بزند که شانه به شانه همه مردم روی زمین تقریباً اندازه رود آیلند را اشغال می کنند چه می شود. برای بحث، اجازه دهید بگوییم که شما به صندلی و توالت نیاز دارید و چه چیزی برای این تعداد زیاد، بنابراین برای جا دادن همه افراد روی زمین در یک هواپیما به اندازه دو برابر جزیره رود یا کمی بیشتر نیاز دارید. برخلاف این سوال، میتوانیم هواپیمای 4-8 طبقه (یا هر مقدار) را بسازیم. یک فرد FAA به طور متوسط حدود 180 پوند (81.65 کیلوگرم) وزن دارد، بنابراین شما باید بلند کنید
1,260,000,000,000 پوند یا 630,000,000 تن (572,000,000,000 کیلوگرم یا 572,000,000 تن متریک)
برای ارائه یک چارچوب مرجع، A380 دارای حداکثر بار ساختاری 330300 پوند (149822 کیلوگرم) است. به خاطر داشته باشید که این فقط محموله است، همچنین باید وزن بدنه هواپیما، موتورها و سوخت را بلند کنید (اگر واقعاً می خواهید به هر جایی بروید). بنابراین اساساً شما به یک هواپیمای چند سطحی نزدیک به اندازه رود آیلند نیاز دارید که بیشترین نیروی رانش ترکیبی موجود در سیاره را داشته باشد و مشروب کافی برای حفظ آرامش همه برای پرواز داشته باشد.
مسئله ساختاری در برخی موارد به بارگذاری بال خلاصه می شود. یکی از محدودیتهایی که امروزه خود تحمیل میشود این است که بیشتر هواپیماها تک هواپیماهای معمولی با بال پایین هستند، بنابراین ما چیزها را در ارتباط با آن میبینیم. به عبارت دیگر ممکن است بدنه در مورد نقاط نصب بال فشار بیاورد و بالها عموماً بلند و پایین هستند، اما چیزی مانع از استفاده از طرح جایگزین با چند بال یا طراحی بدنه بالابر کامل برای انجام ساختار مورد نیاز ما نمی شود. به این ترتیب می توان بر ایده بال های بزرگ غلبه کرد و از نظر تاریخی این مشکل در هوانوردی اولیه (سه هواپیما و غیره) اینگونه حل شد. . اگر فقط در حال ساختن یک هواپیمای غول پیکر هستیم، می توانیم از جت ها، موشک ها و انواع دستگاه های رانش بالا برای اهداف علمی استفاده کنیم. اگر هواپیمای سیمانی شکل درستی داشت و نیروی رانش کافی داشتید، میتوانید پرواز کنید.
به یاد داشته باشید اگر Thrust > Drag and Lift > Weight شما پرواز خواهید کرد (این را روز اول در مدرسه پرواز یاد گرفتم). انجام این کار به صورت کنترل شده و سازماندهی شده زمان قابل توجهی بیشتری برای یادگیری می برد.
از آنجایی که سؤال برای درگیر کردن تعداد مسافران ویرایش شده است، مسائل دیگری نیز وجود دارد.
شما باید به طور واقع بینانه هواپیما را بارگیری و تخلیه کنید که زمان می برد. هواپیمایی که بارگیری و تخلیه آن بیش از حد طول می کشد، برای کار به صرفه نخواهد بود.
شما به دلیلی نیاز دارید تا تعداد زیادی از افراد را به یکباره به این اندازه دور کنید.
بسته به طول پرواز، باید غذا، آب و دستشویی را در نظر بگیرید تا همه را در خود جای دهد (مخازن زباله بی نهایت بزرگ نیستند).
آیا حتی افراد به اندازه کافی در یک مکان وجود دارند؟ هواپیماها مردم (و اغلب اجسام) را از یک مکان به مکان دیگر جابجا می کنند، اما بیایید برای مثال نیویورک را در نظر بگیریم که جمعیتی حدود 8.5 میلیون نفر دارد، احتمال اینکه همه آنها به یک مکان به یک مکان بروند نزدیک به 0٪ است. بنابراین شما به یک هواپیمای مسافربری 8.5 میلیونی نیاز ندارید، اما می توانید کمی کوچکتر شروع کنید.
از دیدگاه خطوط هوایی (مردمی که در واقع خرید می کنند) هواپیماهایی مانند 747 در حال حاضر به اندازه کافی بزرگ و گران هستند. بوئینگ 747 در آن زمان تقریباً ورشکست شده بود، اما از آن زمان تا کنون عملکرد نسبتاً موفقی داشته است. A380 نسبتا جدید است اما جالب است که ببینیم چگونه بازی را تغییر می دهد.
با توجه به سیاره به اندازه کافی بزرگ با جمعیت کافی، محدودیت نظری وجود ندارد. اما چندین محدودیت عملی وجود دارد.
جرم گیری وزن
مهمترین و بد درک شده توسط چندین پاسخ در اینجا، مسئله وزن است. در جایی که یک پرنده جسمی جامد است و با مکعب دهانه اش فلس می شود، هواپیما یک پوسته توخالی، یک سطح است، و بنابراین در واقع با (اسمایی) مربع دهانه اش فلس می شود. این پیامدهای مهمی دارد.
با نادیده گرفتن عدد رینولدز، یک پروفیل بال فقط می تواند بارگذاری یکسان (وزن در واحد سطح) را در هر مقیاسی تحمل کند. ابعاد دو برابر به معنای چهار برابر مساحت و چهار برابر ظرفیت بالابری است.
با همان بارگذاری بال، پوست تحت فشار نیازی به ضخیم تر شدن ندارد. بنابراین وزن آن تنها چهار برابر بیشتر است.
یک I-spar در عمق دو برابر می شود. استحکام مقدار معینی از مواد با مجذور عمق آن افزایش مییابد، بنابراین میتواند چهار برابر تنش را که وزن هواپیما را به حساب میآورد، برای همان مقدار ماده تحمل کند. به جز، اسپار در حال حاضر دو برابر بیشتر است. استرس نیز متناسب با آن است، بنابراین دو برابر می شود. بنابراین شما به دوبرابر سطح مقطع، دو برابر طول نیاز دارید، که وزن اسپار را در مجموع چهار برابر وزن می کند.
بنابراین از نظر تئوری می توان اندازه را به طور نامحدود افزایش داد، با افزایش تعداد مسافران با مربع طول بال ها. اما در نهایت، محدودیتهای عملی وارد میشوند.
یک مشکل این است که پوست به سفت کننده های بیشتری (دنده ها و اسپارهای فرعی) برای جلوگیری از چروک شدن آن نیاز دارد. اینها خود باید توسط قطعات متقاطع بیشتری مهار شوند. این تکه های متقاطع باید سفت تر باشند تا بتوانند با دوبرابر طولانی تر بودن کنار بیایند. وب یک I-spar (بیت عمودی) یک مثال است. طراحان با دوک نگه داشتن اعضای مختلف و افزودن سفت کننده های فرعی بیشتر برای نگه داشتن قطعات اصلی در موقعیت خود، با این روش مقابله می کنند.
اما عملی بودن ساخت و مواد باعث می شود تا چه اندازه می توانید با این همه پیش بروید و گران است. مگر اینکه خیلی حیله گر نباشید، به زودی به نقطه ای می رسید که اضافه کردن یک سطح دیگر از سفت کننده ها به وزن دیگری نیز اضافه می کند. بنابراین در برخی مواقع طراحی نمی تواند بزرگتر شود، و وزن شروع به خزش با بریدن گوشه ها (یا، بهتر است بگوییم، پر شدن!) برای کاهش ساخت و هزینه ها می کند.
سطوح را کنترل کنید
همچنین مشکلی در اختیار کنترل و پاسخگویی هواپیماهای بزرگ وجود دارد. یک هواپیمای چهار برابر مساحت، چهار برابر نیروی کنترلی اعمال می کند. بال چهار برابر وزن دارد، بنابراین با همان سرعت شتاب می گیرد. اما همچنین برای رسیدن به همان زاویه کرانه دو برابر فاصله دارد، بنابراین رسیدن به آنجا بیشتر طول می کشد. اگر هیچ تغییری در سیستم کنترل ایجاد نشود، هواپیما به آرامی پاسخ می دهد و خلبانان باید زودتر تصمیم بگیرند. اگر نیاز به اصلاح فوری پرواز باشد، این می تواند خطرناک باشد.
بنابراین هواپیماهای بزرگ دارای سطوح کنترل پرواز اضافی هستند، مانند اسپویلر بال، فلاپرون داخلی، سطوح دم بزرگتر و موارد مشابه. واضح است که برای جدا کردن قطعات بیشتر و بزرگتر از یک بال با دهانه بیشتر و در عین حال سفت نگه داشتن آن از نظر ساختاری، محدودیتی وجود دارد. علاوه بر این، سطوح کنترل بزرگتر با زمان پاسخ کند دچار همین مشکل می شوند.
سیستم ها خزش می کنند
همه اینها مسائل بیشتری را در مورد میزان کنترل، نظارت و تجهیزات مربوطه به منظور پرواز هواپیما به همراه دارد. چرخهای فرود به جای بزرگتر شدن، بیشتر میشوند. سطوح کنترلی پیچیده و عظیم و ارابه فرود به سیستمهای کنترلی پیچیده و عظیم نیاز دارند، فضای بار بزرگتر طراح را به تناسب داخلی پیچیدهتر وسوسه میکند، مکعبکردن هوا میتواند تدارک اطفاء حریق، تهویه و تهویه و غیره را فراهم کند. در عمل، مقیاس هواپیماهای بزرگ بیشتر از مربع دهانه است، اگرچه بسیار کمتر از مکعب.
اهداف دیگری مانند کمک به بازرسی خدمه، سیگنال دادن به خدمه زمینی، تهویه اضافی، خروج دود و غیره وجود دارد (همچنین می توان از آن برای پرتاب اشیا به بیرون استفاده کرد، اگرچه به طور کلی توصیه نمی شود). به نظر می رسد یکی از دلایل اصلی (حداقل در گذشته) بهبود دید خلبان در مواردی که شیشه جلو مات می شود، باشد.
پنجره ها در همه هواپیماها یافت نمی شوند (مثلاً 787 آن را ندارد) و باز کردن آن خیلی آسان نیست (توجه داشته باشید که به سمت داخل باز می شود).
ابتدا یک مکانیسم قفل وجود دارد، سپس یک میل لنگ که کل مجموعه پنجره از جمله قاب را حرکت می دهد، یا یک اهرم برای حرکت مجموعه پنجره. هنگامی که پنجره بسته و قفل است، بسته می شود. وقتی باز است، مانند پنجره ماشین شما از قاب جدا نمی شود.
(ب) شرایط بارندگی. برای شرایط بارندگی موارد زیر اعمال می شود:
(1) هواپیما باید وسیله ای برای حفظ قسمتی از شیشه جلو در شرایط بارندگی داشته باشد، به طوری که هر دو خلبان بتوانند دید وسیعی در طول مسیر پرواز در حالت پرواز عادی هواپیما داشته باشند.
(3) اولین خلبان باید پنجره ای داشته باشد که-
(i) در شرایطی که کابین تحت فشار نباشد تحت شرایط مقرر در بند (ب) (1) این بخش قابل باز شدن است.
(4) پنجره قابل باز شدن مشخص شده در بند (ب) (3) این بخش نیازی به ارائه ندارد اگر نشان داده شود که سطحی از سطح شفاف به اندازه کافی برای حداقل یک خلبان برای فرود ایمن هواپیما در این صورت شفاف باقی می ماند. از-
(ii) برخورد با تگرگ شدید، پرندگان یا حشرات.
در یک کابین تحت فشار، تهیه پنجره ایده خوبی نیست. (علاوه بر افزایش وزن)، اگر کسی بتواند پنجره را باز کند، دستوری برای فاجعه خواهد بود (کاهش فشار -> ماسک های اکسیژن -> زمین).
*بسیاری از هواپیماها دارای طناب های فرار هستند که در یک محفظه بالای پنجره در هر طرف کابین خلبان نصب شده اند، مانند کابین خلبان A320
آیا استفاده از انرژی باد در هواپیما معقول است؟در واقع ایده ساخت یک هواپیمای الکتریکی است که انرژی آن از خورشید و باد در هنگام فرود هواپیما تامین شود. به جای استفاده از اسپویلر به عنوان ترمز هوا، این توربینهای بادی که به طور جداگانه نصب میشوند، میتوانند انرژی دراگ و مهار را به طور همزمان اضافه کنند. به عبارت دیگر ترمز احیا کننده.به طور معمول خیر: استخراج انرژی از جریان هوا باعث ایجاد نیروی پسا می شود که باید با رانش اضافه بر آن غلبه کرد. از آنجایی که هر شکلی از تبدیل انرژی باعث تلفات می شود، باید انرژی رانش بیشتری نسبت به جریان هوا اضافه شود.
تنها زمانی که موتورها از کار بیفتند و ژنراتورها از کار بیفتند، استخراج انرژی از جریان هوا منطقی است. در هواپیما دو کاربرد وجود دارد که توسط "انرژی باد" هدایت می شود:
هواپیماهای قدیمیتر از ژیروسها برای افق مصنوعی استفاده میکنند که توسط هوای قوچ تغذیه میشوند. به این ترتیب ژیروسکوپ ها حتی پس از خرابی موتور نیز کار می کنند.
جتها از توربینهای هوایی Ram (RAT) استفاده میکنند، ژنراتورهای پروانهای که در زمانی که سایر ابزارهای تولید برق و نیروی هیدرولیک از کار افتاده باشند، به جریان هوا منتقل میشوند. توجه داشته باشید که این کار در پرواز بدون نیرو انجام می شود و میزان فرورفتگی را افزایش می دهد. با تمرکز جدید سوال شما بر نیروی محرکه الکتریکی، پاسخ متفاوت خواهد بود. اکنون به احتمال زیاد ملخ هایی خواهید داشت که با موتورهای الکتریکی کار می کنند. در هنگام فرود، آنها می توانند معکوس عمل کنند و باتری را شارژ کنند، که به احتمال زیاد تا زمان فرود هواپیما خالی می شود. این را می توان در طول نزدیک شدن نهایی تا پایان ران اوت پس از تاچ داون انجام داد. می توان انتظار داشت که هر هواپیمای برقی دارای L/D بالایی باشد، بنابراین استفاده از ترمزهای سرعت برای ایجاد یک رویکرد تندتر منطقی است.
با این حال، اگر یک دستگاه اضافی مقرون به صرفه باشد، تعجب می کنم. این شارژ مجدد باید توسط سیستم پیشرانه معمولی انجام شود، در غیر این صورت در بیشتر طول پرواز به وزن مرده اضافه می شود.
شما فرمولها را درخواست کردید، اما تنها چیزی که میتوانم در اینجا ارائه کنم، محاسبات پشت پاکت است. ابتدا باید گفت که ملخهای گام متغیر مانند آسیابهای بادی سست خواهند بود، زیرا پیچ و خم آنها برای حالت آسیاب بادی اشتباه است. من انتظار دارم که راندمان آنها حدود 30٪ باشد، به این معنی که تنها 30٪ از انرژی استخراج شده توسط درگ به انرژی مکانیکی تبدیل می شود که موتور الکتریکی را به حرکت در می آورد.
در مرحله بعد، راه اندازی یک موتور الکتریکی به عنوان یک ژنراتور مجدداً مستلزم مصالحه است. موتورهای خوب ژنراتورهای ضعیفی را ایجاد می کنند و سیم کشی مجدد موتور برای عملکرد بهتر ژنراتور باعث کاهش کارایی آن در استفاده معمولی می شود. وقتی موتور معکوس منطقی به نظر می رسد، به سرعت بیش از آنچه در مرحله پرواز کوتاه به دست می آورید، ضرر خواهید کرد.حال بیایید فرض کنیم که شما سیستم پیشرانه خود را در بالاترین بازده (مثلاً 90%) نگه دارید و بپذیرید که تنها 10٪ از انرژی دراگ را به انرژی الکتریکی تبدیل می کند. اجازه دهید همچنین فرض کنیم که هواپیمای خورشیدی آینده شما دارای L/D 30 است که برای یک رویکرد عملی باید به 10 کاهش یابد. شما این کار را از 1000 فوت به پایین انجام میدهید و از پروانه آسیاب بادی نیز در هنگام خروج استفاده میکنید. سرعت تقریب v، جرم m و انرژی اولیه هواپیما$305\cdot m\cdot 9.81 + \frac{m}{2} \cdot v^2$ است. دو سوم انرژی پتانسیل وارد کشش پروانه می شود، و برای اینکه سخاوتمندانه باشیم، فرض می کنیم که 100٪ انرژی جنبشی نیز به کشش پروانه می رود، حتی اگر نیروی ترمز پروانه ها در سرعت پایین واقعا ضعیف است و نیاز به پشتیبانی از چرخ دارد. ترمزها
اکنون مهم است که هواپیمای شما با چه سرعتی پرواز می کند، زیرا این امر باعث تغییر نسبت بین انرژی پتانسیل و انرژی جنبشی می شود. برای ساده نگه داشتن همه چیز، من هر دو را با انرژی مورد نیاز برای پرواز بعدی مرتبط خواهم کرد. 10٪ از انرژی جنبشی کامل هواپیما را به کمتر از یک سوم سرعت پرواز شتاب می دهد - پس از این، 91٪ انرژی باقی مانده برای رسیدن به v باید با شارژ باتری ها در بین پروازها اضافه شود.
انرژی الکتریکی گرفته شده از انرژی پتانسیل به شما کمک می کند تا ارتفاع 60 فوتی بالا بروید یا پرواز در سطح v را برای مسافت 1800 فوت حفظ کنید. در L/D 30 هواپیما مسافت 30000 فوتی را بدون رانش پرواز می کند و با ترمز کردن شما انرژی را برای پوشش 20000 فوت استخراج می کنید که با راندمان تبدیل 10% (و 90% راندمان نیروی محرکه!) شما را با خود می برد. فقط 1800 فوت
اجازه دهید ابتدا روی فرود از ارتفاع کروز تا نزدیک شدن نهایی تمرکز کنیم. در حالت ایدهآل، این فرود با موتورهایی انجام میشود که در پایینترین حالت رانش (بیکار پروازی) قرار دارند، به این معنی که موتورها نیرو را برای سیستمهای مختلف الکتریکی و هیدرولیک، و فشار، و کمی رانش فراهم میکنند، زیرا واقعاً نمیتوانید از آن اجتناب کنید. روی یک جت از نظر تئوری، این می تواند توسط یک توربین هوایی Ram انجام شود (حالا فرض کنیم که هواپیمای فرضی ما مجهز به نسخه نسبتاً بزرگی است که به راحتی تمام سیستم های فوق الذکر را تغذیه می کند، زیرا یک RAT معمولی فقط می تواند قدرت اضطراری محدودی را ارائه دهد). با این حال، این کشش را تا حد زیادی افزایش می دهد و برای حفظ سرعت، مشخصات فرود تندتر خواهد بود. این به نوبه خود به این معنی است که هواپیما باید زمان بیشتری را در ارتفاع کروز بگذراند، که برای نگهداری آن نیاز به انرژی دارد.
راه دیگری برای بررسی این موضوع، یک تراز انرژی ساده است: مقدار محدودی از انرژی پتانسیل وجود دارد، و واقعاً مهم نیست که از آن فقط برای حفظ سرعت استفاده میکنید یا از آن برای حفظ سرعت و ترمز احیاکننده استفاده میکنید. ، زیرا مقدار کل انرژی که می توانید از آن استخراج کنید همیشه یکسان است.
البته یک لحظه وجود دارد که هواپیماها باید ترمز کنند و آن بعد از تاچ داون است. بیایید فعلاً فرض کنیم که از محیط زیست بسیار آگاه هستیم و از هیچ وسیله دیگری برای ترمز به جز سیستم ترمز احیا کننده استفاده نمی کنیم. هواپیما هنوز با سرعتی در حدود 130 کیلو در ساعت، 240 کیلومتر در ساعت یا 150 مایل در ساعت حرکت می کند، بنابراین مطمئناً این به ما انرژی زیادی می دهد؟ بیایید برای تعدادی از ارقامی که برای یک بوئینگ 737-300 پیدا کردم، یک محاسبه پشت پاکت انجام دهیم.
فرض کنید با وزن 60000 کیلوگرم (نزدیک به MLW) با فلپ های کاهش یافته به 15 فرود می آییم، که سرعت فرود 158kts=81.3m/s را به ما می دهد. مقدار انرژی جنبشی 12mv2≈200MJ است (بله، این مگا ژول است!). این خیلی انرژی است، نه؟! خوب... نه واقعا. نفت سفید (که تقریباً مشابه سوخت جت است) با چگالی انرژی در حدود 46 مگا ژول بر کیلوگرم تولید می شود. ما در مورد چیزی معادل کمی بیش از 4 کیلوگرم نفت سفید صحبت می کنیم، در هواپیمایی که حدود 16000 کیلوگرم از آن را حمل می کند. این بدان معناست که ما حدود 0.025 درصد از ظرفیت سوخت را بازسازی می کنیم.
من آن را به عنوان تمرینی به خواننده می سپارم تا فکر کند که آیا می توان یک سیستم ترمز احیا کننده طراحی کرد، به طوری که سوخت اضافی مورد استفاده به دلیل وزن و اندازه آن کمتر از 0.025٪ باشد.
بیایید محاسبه را روی هواپیمایی انجام دهیم که در واقع بیشتر تجهیزات لازم (باتری ها و موتورهای الکتریکی که احتمالاً می توانند به عنوان دینام یا دینام عمل کنند) را در هواپیما دارد: Solar Impulse 2. ظرفیت باتری فوق العاده 4x41kWh (590MJ) دارد. با فرض یکسان بودن سرعت برخاستن و فرود (20kts=36km/h=10m/s) و با وزن بارگذاری شده 2300 کیلوگرم، انرژی جنبشی هنگام فرود 115 کیلوژول است. این 0.0195 درصد ظرفیت باتری است - تقریباً مشابه نمونه B733 ما! و توجه داشته باشید که این دوباره با فرض بازیابی 100% انرژی جنبشی پروانه ها است... این ایده هرگز عملی نخواهد شد. (برای مقایسه، کمتر از دو ثانیه انرژی تولید شده توسط پنل های خورشیدی در اوج رتبه مربوطه است)توربین های بادی روی زمین می ایستند و توده هوا با سرعتی از آنها عبور می کند، بنابراین انرژی جنبشی دارد. اما هواپیما نسبت به باد در حال حرکت است، بنابراین باد قاب استراحت است و انرژی ندارد. بنابراین وقتی هواپیما از جریان هوا و/یا فشار هوا استفاده می کند، از انرژی خود استفاده می کند نه باد¹.
البته اکنون توربین نصب شده روی هواپیما انرژی تولید می کند. اما این به هزینه انرژی هواپیما خواهد بود. هنگام پرواز در سطح زیر قدرت، نیرو از موتورها می آید، بنابراین استخراج مستقیم آن از طریق ژنراتور نصب شده روی درایو جانبی کارآمدتر است. اما حتی زمانی که هواپیما در حالت بیکار فرود میآید، انرژی بالقوه آن هزینه میشود و این انرژی در ابتدا توسط موتورها در هنگام صعود تامین میشد. خاموش کردن زودتر موتور و استفاده از تمام آن برای جبران درگ در هنگام سر خوردن کارآمدتر است.
این در مورد موتور گلایدر خورشیدی مانند هر هواپیمای دیگری صدق می کند. توقف زودتر موتورها و سر خوردن در حول و حوش بهترین زاویه لغزش کارآمدتر از کارکردن بیشتر موتورها و سپس تولید مجدد انرژی است، زیرا نه تبدیل انرژی الکتریکی به انرژی پتانسیل از طریق موتور و پروانه و نه تبدیل از انرژی پتانسیل به انرژی الکتریکی از طریق توربین و ژنراتور بسیار کارآمد است.
و حتی در هنگام استفاده از مواد حرارتی یا دیگر هوای افزایش دهنده برای به دست آوردن انرژی بالقوه نیز کاربرد دارد. دوباره کارآمدتر است که از تبدیل انرژی اجتناب کنید و به سادگی از حرارت برای به دست آوردن ارتفاع استفاده کنید و در حالی که انرژی الکتریکی را مستقیماً از پانل های خورشیدی دریافت می کنید، لغزش را افزایش دهید.
همچنین وزن عامل محدود کننده مهم برای موتور گلایدر خورشیدی خواهد بود. این بدان معناست که شما نمیتوانید باتریهای زیادی را سوار کنید و به نوبه خود به این معنی است که ترمز احیاکننده چندان مفید نخواهد بود زیرا ظرفیت زیادی برای ذخیره انرژی ندارید. همچنین به این معنی است که ممکن است بخواهید از توربین اختصاصی برای کاهش وزن خودداری کنید. شما همچنان قادر خواهید بود مقداری انرژی را از پروانه های آسیاب بادی با راندمان کمتری دوباره تولید کنید. اما همانطور که توضیح داده شد، آنقدرها هم منطقی نیست.
تنها زمانی که هواپیما از توربین استفاده می کند در شرایط اضطراری است. هنگامی که همه موتورها از کار می افتند، از توربین هوای رم برای تامین انرژی سیستم های الکتریکی و هیدرولیک ضروری استفاده می شود. مسافت سر خوردن را کمی کوتاه می کند، اما اگر منبع تغذیه دیگری در دسترس نباشد ارزشش را دارد.
تا آنجایی که باد پیش می رود، تنها کاربرد عملی باد، انتخاب مسیر است که تا حد امکان باد دنباله دار در طول سفر دریایی وجود داشته باشد. برای مثال مسیرهای اقیانوس اطلس شمالی به طور دوره ای تنظیم می شوند تا به پروازهای شرق اجازه استفاده از جت استریم را بدهد. به یک معنا، این از انرژی باد استفاده می کند، زیرا هواپیما برای رسیدن به مقصد سوخت کمتری می سوزاند.
¹ انرژی کمیت عجیبی است. در تمام قاب های مرجع اینرسی حفظ می شود، اما برخی از اشکال آن در هر یک مقادیر متفاوتی خواهند داشت. شما می توانید یک چارچوب مرجع را انتخاب کنید که در آن باد انرژی داشته باشد، اما منطقی تر خواهد بود.
آیا حداکثر اندازه ممکن برای یک هواپیما وجود دارد؟
تصادفی نیست که بزرگترین پرندگان پرواز نمی کنند. توانایی پرواز با افزایش اندازه کاهش می یابد، بنابراین محدودیت بالایی برای هواپیما نیز وجود دارد. دلیل اصلی این است که با افزایش اندازه، تودهها با افزایش اندازه مکعب بالا میروند در حالی که ساختارهای باربر مانند سطح مقطع بال اسپار تنها با افزایش مربع اندازه رشد میکنند. این قانون قدرت ساده ترین قوانین مقیاس بندی است.
از آنجایی که بارهای روی بال هواپیما نه تنها به اندازه آن، بلکه به بسیاری از پارامترهای دیگر (زاویه حمله، سرعت، نسبت ابعاد ...) بستگی دارد، هیچ مرز مشخصی وجود ندارد و پیشرفت در مواد کمک می کند تا محدودیت اندازه را تغییر دهد. اگر کسی بخواهد بزرگترین هواپیمای دنیا را بسازد، طول بالها به راحتی میتواند دو برابر اندازه بزرگترین هواپیماهای امروزی باشد، اما کاربرد این هواپیما بسیار محدود خواهد بود.
استفاده از این هواپیما برای سفر مسافران محدودیتهای بیشتری مانند تعداد خروجیهای اضطراری و حداکثر فاصله تا نزدیکترین خروجی را اضافه میکند، اما با استفاده از چندین بدنه کوچکتر میتوان بر این مسئله غلبه کرد. یک هواپیمای دو بدنه نیز وزن محموله را پخش می کند، بنابراین بال خمش ریشه کاهش می یابد.
بلافاصله محدودیت اندازه را به میزان قابل توجهی افزایش می دهد. با این حال، برای برخاستن از آن به باندهای جدید و عریضتری نیاز دارد. و افزودن بدنه بیشتر به همان بال به زودی با مشکلات بال زدن مواجه خواهد شد.
نشانه بعدی می تواند طرح هایی باشد که مورد مطالعه قرار گرفته و امکان پذیر بوده است اما در نهایت به دلایل اقتصادی ساخته نشده اند. در اینجا بزرگترین وسایل نقلیه اثر زمینی هستند: پرواز آهسته در هوای متراکم محدودیت اندازه را بالا می برد. بوئینگ پلیکان با طول بال 152 متر برنامه ریزی شده بود و بریف بال را با 2500 تن جرم برخاستن و 125.5 متر طول بال پیشنهاد کرد.
من حدس میزنم که طول بالهای 200 متری هنوز امکانپذیر است، و هنگام پخش وزن حتی 500 متر باید واقعبینانه باشد،
بله، حد بالایی وجود دارد، اما این حد بالا ممکن است با نوآوری های تکنولوژیکی تغییر کند.
یک هواپیما به دلیل ضریب بالابر $L=\frac12\rho v^2 A C_L$ پرواز می کند، با v سرعت هوا، که ترکیبی از سرعت هواپیما و سرعت باد است، ρ≈1kg m-3 در حداقل نظری ارتفاع 5 کیلومتر (به یاد داشته باشید که بیشتر هواپیماها به 10 کیلومتر می رسند، اما من برای نشان دادن حد بالایی)، A مساحت، و CL یک ضریب با مقدار معمولی کمتر از 2، که ممکن است با نوآوری های تکنولوژیکی تغییر کند، کمی افراطی تر در نظر گرفتم.
بنابراین تنها عواملی که میتوانیم بر آنها تأثیر بگذاریم v و A هستند. با این حال، اگر A را افزایش دهیم، جرم m سریعتر از ناحیه A افزایش مییابد زیرا برای جلوگیری از شکستن شکل صفحه تحت نیروهای عظیم، مواد بیشتری مورد نیاز است. افزایش درجه دوم A بیش از یک درجه دوم بر حسب m می دهد و بنابراین در L مورد نیاز.
اگر v را افزایش دهیم به سوخت بیشتری نیاز داریم. مقدار سوخت در واحد مسافت به صورت خطی در v افزایش می یابد، زیرا به صورت درجه دوم در واحد زمان در v افزایش می یابد. بنابراین L به صورت درجه دوم افزایش می یابد که m فقط به صورت خطی افزایش می یابد. این بدان معنی است که ما ممکن است با افزایش v کاری انجام دهیم. این بدان معناست که هواپیماها باید قبل از بلند شدن سریعتر حرکت کنند، که به خطوط بلندتری نیاز دارد. توجه داشته باشید که ما نمی توانیم به افزایش v ادامه دهیم زیرا نمی توانیم کنترل خود را از دست بدهیم.
به طور خلاصه، چیزهایی که ما می توانیم بهبود دهیم عبارتند از v، سرعت، CL، با نوآوری های تکنولوژیکی و ρ با کاهش ارتفاع پرواز. با این حال، عملی نیست.هیچ باندی وجود ندارد که بتواند چنین هواپیمایی را تحمل کند. هواپیماهایی مانند A380 و 747 در حال حاضر به دلیل ظرفیت طول/وزن باند مسیر محدود شدهاند. شما باید باندهای فرودگاه را تغییر دهید تا هر چیزی به طور قابل توجهی بزرگتر انجام شود. البته با این فرض که به روشی مشابه بیشتر هواپیماهای مسافربری فرود می آید (یعنی نه VTOL)
چه مسیری قرار است پرواز کند؟ اندازه هواپیماها به این دلیل نیست که نمیتوانیم آنها را بزرگتر بسازیم، آنها به اندازه آنها هستند زیرا مسیرها به آنها دیکته میکنند که این اندازه باشند. آیا واقعاً نیاز دارید که 1000 نفر را در یک مسیر معین به طور همزمان جابجا کنید؟ چند مسیر اینقدر تراکم سفر دارند؟
بیایید به صورت فرضی به این موضوع نگاه کنیم، Jamiec به نکته بسیار خوبی اشاره میکند که هواپیمای دارای ظرفیت بیش از 7 میلیارد بیفایده است، بنابراین بیایید آن را حداکثر در نظر بگیریم. اگر XKCD در یک سوال مشابه این موضوع را پوشش دهد و تخمین بزند که شانه به شانه همه مردم روی زمین تقریباً اندازه رود آیلند را اشغال می کنند چه می شود. برای بحث، اجازه دهید بگوییم که شما به صندلی و توالت نیاز دارید و چه چیزی برای این تعداد زیاد، بنابراین برای جا دادن همه افراد روی زمین در یک هواپیما به اندازه دو برابر جزیره رود یا کمی بیشتر نیاز دارید. برخلاف این سوال، میتوانیم هواپیمای 4-8 طبقه (یا هر مقدار) را بسازیم. یک فرد FAA به طور متوسط حدود 180 پوند (81.65 کیلوگرم) وزن دارد، بنابراین شما باید بلند کنید
1,260,000,000,000 پوند یا 630,000,000 تن (572,000,000,000 کیلوگرم یا 572,000,000 تن متریک)
برای ارائه یک چارچوب مرجع، A380 دارای حداکثر بار ساختاری 330300 پوند (149822 کیلوگرم) است. به خاطر داشته باشید که این فقط محموله است، همچنین باید وزن بدنه هواپیما، موتورها و سوخت را بلند کنید (اگر واقعاً می خواهید به هر جایی بروید). بنابراین اساساً شما به یک هواپیمای چند سطحی نزدیک به اندازه رود آیلند نیاز دارید که بیشترین نیروی رانش ترکیبی موجود در سیاره را داشته باشد و مشروب کافی برای حفظ آرامش همه برای پرواز داشته باشد.
مسئله ساختاری در برخی موارد به بارگذاری بال خلاصه می شود. یکی از محدودیتهایی که امروزه خود تحمیل میشود این است که بیشتر هواپیماها تک هواپیماهای معمولی با بال پایین هستند، بنابراین ما چیزها را در ارتباط با آن میبینیم. به عبارت دیگر ممکن است بدنه در مورد نقاط نصب بال فشار بیاورد و بالها عموماً بلند و پایین هستند، اما چیزی مانع از استفاده از طرح جایگزین با چند بال یا طراحی بدنه بالابر کامل برای انجام ساختار مورد نیاز ما نمی شود. به این ترتیب می توان بر ایده بال های بزرگ غلبه کرد و از نظر تاریخی این مشکل در هوانوردی اولیه (سه هواپیما و غیره) اینگونه حل شد. . اگر فقط در حال ساختن یک هواپیمای غول پیکر هستیم، می توانیم از جت ها، موشک ها و انواع دستگاه های رانش بالا برای اهداف علمی استفاده کنیم. اگر هواپیمای سیمانی شکل درستی داشت و نیروی رانش کافی داشتید، میتوانید پرواز کنید.
به یاد داشته باشید اگر Thrust > Drag and Lift > Weight شما پرواز خواهید کرد (این را روز اول در مدرسه پرواز یاد گرفتم). انجام این کار به صورت کنترل شده و سازماندهی شده زمان قابل توجهی بیشتری برای یادگیری می برد.
از آنجایی که سؤال برای درگیر کردن تعداد مسافران ویرایش شده است، مسائل دیگری نیز وجود دارد.
شما باید به طور واقع بینانه هواپیما را بارگیری و تخلیه کنید که زمان می برد. هواپیمایی که بارگیری و تخلیه آن بیش از حد طول می کشد، برای کار به صرفه نخواهد بود.
شما به دلیلی نیاز دارید تا تعداد زیادی از افراد را به یکباره به این اندازه دور کنید.
بسته به طول پرواز، باید غذا، آب و دستشویی را در نظر بگیرید تا همه را در خود جای دهد (مخازن زباله بی نهایت بزرگ نیستند).
آیا حتی افراد به اندازه کافی در یک مکان وجود دارند؟ هواپیماها مردم (و اغلب اجسام) را از یک مکان به مکان دیگر جابجا می کنند، اما بیایید برای مثال نیویورک را در نظر بگیریم که جمعیتی حدود 8.5 میلیون نفر دارد، احتمال اینکه همه آنها به یک مکان به یک مکان بروند نزدیک به 0٪ است. بنابراین شما به یک هواپیمای مسافربری 8.5 میلیونی نیاز ندارید، اما می توانید کمی کوچکتر شروع کنید.
از دیدگاه خطوط هوایی (مردمی که در واقع خرید می کنند) هواپیماهایی مانند 747 در حال حاضر به اندازه کافی بزرگ و گران هستند. بوئینگ 747 در آن زمان تقریباً ورشکست شده بود، اما از آن زمان تا کنون عملکرد نسبتاً موفقی داشته است. A380 نسبتا جدید است اما جالب است که ببینیم چگونه بازی را تغییر می دهد.
با توجه به سیاره به اندازه کافی بزرگ با جمعیت کافی، محدودیت نظری وجود ندارد. اما چندین محدودیت عملی وجود دارد.
جرم گیری وزن
مهمترین و بد درک شده توسط چندین پاسخ در اینجا، مسئله وزن است. در جایی که یک پرنده جسمی جامد است و با مکعب دهانه اش فلس می شود، هواپیما یک پوسته توخالی، یک سطح است، و بنابراین در واقع با (اسمایی) مربع دهانه اش فلس می شود. این پیامدهای مهمی دارد.
با نادیده گرفتن عدد رینولدز، یک پروفیل بال فقط می تواند بارگذاری یکسان (وزن در واحد سطح) را در هر مقیاسی تحمل کند. ابعاد دو برابر به معنای چهار برابر مساحت و چهار برابر ظرفیت بالابری است.
با همان بارگذاری بال، پوست تحت فشار نیازی به ضخیم تر شدن ندارد. بنابراین وزن آن تنها چهار برابر بیشتر است.
یک I-spar در عمق دو برابر می شود. استحکام مقدار معینی از مواد با مجذور عمق آن افزایش مییابد، بنابراین میتواند چهار برابر تنش را که وزن هواپیما را به حساب میآورد، برای همان مقدار ماده تحمل کند. به جز، اسپار در حال حاضر دو برابر بیشتر است. استرس نیز متناسب با آن است، بنابراین دو برابر می شود. بنابراین شما به دوبرابر سطح مقطع، دو برابر طول نیاز دارید، که وزن اسپار را در مجموع چهار برابر وزن می کند.
بنابراین از نظر تئوری می توان اندازه را به طور نامحدود افزایش داد، با افزایش تعداد مسافران با مربع طول بال ها. اما در نهایت، محدودیتهای عملی وارد میشوند.
یک مشکل این است که پوست به سفت کننده های بیشتری (دنده ها و اسپارهای فرعی) برای جلوگیری از چروک شدن آن نیاز دارد. اینها خود باید توسط قطعات متقاطع بیشتری مهار شوند. این تکه های متقاطع باید سفت تر باشند تا بتوانند با دوبرابر طولانی تر بودن کنار بیایند. وب یک I-spar (بیت عمودی) یک مثال است. طراحان با دوک نگه داشتن اعضای مختلف و افزودن سفت کننده های فرعی بیشتر برای نگه داشتن قطعات اصلی در موقعیت خود، با این روش مقابله می کنند.
اما عملی بودن ساخت و مواد باعث می شود تا چه اندازه می توانید با این همه پیش بروید و گران است. مگر اینکه خیلی حیله گر نباشید، به زودی به نقطه ای می رسید که اضافه کردن یک سطح دیگر از سفت کننده ها به وزن دیگری نیز اضافه می کند. بنابراین در برخی مواقع طراحی نمی تواند بزرگتر شود، و وزن شروع به خزش با بریدن گوشه ها (یا، بهتر است بگوییم، پر شدن!) برای کاهش ساخت و هزینه ها می کند.
سطوح را کنترل کنید
همچنین مشکلی در اختیار کنترل و پاسخگویی هواپیماهای بزرگ وجود دارد. یک هواپیمای چهار برابر مساحت، چهار برابر نیروی کنترلی اعمال می کند. بال چهار برابر وزن دارد، بنابراین با همان سرعت شتاب می گیرد. اما همچنین برای رسیدن به همان زاویه کرانه دو برابر فاصله دارد، بنابراین رسیدن به آنجا بیشتر طول می کشد. اگر هیچ تغییری در سیستم کنترل ایجاد نشود، هواپیما به آرامی پاسخ می دهد و خلبانان باید زودتر تصمیم بگیرند. اگر نیاز به اصلاح فوری پرواز باشد، این می تواند خطرناک باشد.
بنابراین هواپیماهای بزرگ دارای سطوح کنترل پرواز اضافی هستند، مانند اسپویلر بال، فلاپرون داخلی، سطوح دم بزرگتر و موارد مشابه. واضح است که برای جدا کردن قطعات بیشتر و بزرگتر از یک بال با دهانه بیشتر و در عین حال سفت نگه داشتن آن از نظر ساختاری، محدودیتی وجود دارد. علاوه بر این، سطوح کنترل بزرگتر با زمان پاسخ کند دچار همین مشکل می شوند.
سیستم ها خزش می کنند
همه اینها مسائل بیشتری را در مورد میزان کنترل، نظارت و تجهیزات مربوطه به منظور پرواز هواپیما به همراه دارد. چرخهای فرود به جای بزرگتر شدن، بیشتر میشوند. سطوح کنترلی پیچیده و عظیم و ارابه فرود به سیستمهای کنترلی پیچیده و عظیم نیاز دارند، فضای بار بزرگتر طراح را به تناسب داخلی پیچیدهتر وسوسه میکند، مکعبکردن هوا میتواند تدارک اطفاء حریق، تهویه و تهویه و غیره را فراهم کند. در عمل، مقیاس هواپیماهای بزرگ بیشتر از مربع دهانه است، اگرچه بسیار کمتر از مکعب.

- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: هوافضا
وسیله نقلیه پرتاب ماهواره دقیقاً چیست؟
موشکی که برای پرتاب ماهواره استفاده می شود "وسیله پرتاب ماهواره" نامیده می شود. یک وسیله نقلیه پرتاب از چندین بخش یا "مرحله" مختلف تشکیل شده است که هر مرحله نقش متفاوتی را بازی می کند.اولین مرحله از وسیله نقلیه پرتاب شامل سوختی است که برای بلند کردن ماهواره و پرتاب وسیله نقلیه از زمین و آسمان مورد نیاز است. این موشک ها باید بسیار قدرتمند باشند زیرا یک وسیله نقلیه پرتاب در هنگام صعود صدها تن وزن دارد. بعد از تمام شدن سوخت ، مرحله اول دیگر لازم نیست و خراب می شود و به زمین می افتد.
مرحله دوم شامل راکت های کوچکتری است که پس از پایان مرحله اول مشتعل می شوند. موشک های مرحله دوم مخازن سوخت خود را دارند. مرحله دوم برای ارسال ماهواره به فضا استفاده می شود. مانند مرحله اول ، بعد از تمام شدن سوخت و سوختن در جو زمین یا عقب افتادن ، آن خراب می شود.
مرحله بالایی وسیله پرتاب به ماهواره متصل می شود ، که در یک محافظ فلزی محصور شده است ، "فیرینگ" نامیده می شود. این نمایشگاه ماهواره را هنگام پرتاب محافظت می کند و حرکت وسیله پرتاب را از طریق مقاومت در برابر جو زمین آسان می کند. وقتی ماهواره بالاتر از جو زمین قرار گرفت و در جو زمین سوخت ، این نیروگاه از هم جدا می شود. موشک های مرحله فوقانی بعد از قرار گرفتن ماهواره در فضا شلیک می کنند و ماهواره را دقیقاً در مکان مورد نیاز قرار می دهند.
هنگامی که وسیله پرتاب از جو زمین خارج شد ، ماهواره از مرحله بالایی جدا می شود. سپس ماهواره به یک "مدار انتقال" فرستاده می شود که ماهواره را بالاتر به فضا می فرستد. ماهواره هنگامی که به ارتفاع مداری دلخواه خود می رسد ، صفحات خورشیدی و آنتن های ارتباطی خود را که در حین پرواز دور نگه داشته شده بود ، باز می کند. سپس ماهواره در مدار خود با ماهواره های دیگر قرار می گیرد
امروزه ، بسیاری از موشک ها بیش از یک ماهواره در مدار را حمل می کنند. اما چگونه یک موشک چند ماهواره را در مدار خود قرار می دهد؟
یک استراتژی نسبتاً رایج این است که دو یا چند ماهواره را روی هم جمع کنید. ماهواره بالایی مستقیماً در داخل تورینگ محموله قرار دارد . هر ماهواره دیگری که در زیر قرار دارد ، به نوعی یک پرده داخلی نشسته است. سیستم های پرتاب دوگانه نامیده می شوند .
بسته به نیاز ماهواره ها ، مرحله بالایی موشک می تواند چندین بار مشتعل شود با این حال ، 'شمع گذاری' ماهواره ها تنها روش نیست. ماهواره ها دقیقاً در کنار یکدیگر پرتاب می شوند و عملاً از یک آداپتور محموله مشترک استفاده می کنند. اگر ماهواره ها به گونه ای ساخته و طراحی شوند می توان این کار را انجام داد ،
این واقعاً به موشک و مأموریت و غیره بستگی دارد. اما به طور کلی همان موضوع مشترک صحبت می شود. فضاپیماها به طور معمول به موشک بارگیری می شوند و توسط نوعی پیچ و مهره انفجاری (یا گیره های دیگر) از نوع فناوری در جای خود نگه داشته می شوند. هنگامی که موشک آماده رها کردن فضاپیما باشد ، پیچ های انفجاری را فعال می کند و باعث می شود فضاپیما با سرعتی از موشک دور شود.
برای پرتاب یک موشک تک مرحله ای ، اندازه خاصی وجود دارد که انرژی مورد نیاز را به حداقل می رساند. وزن موشک شما (فقط بدنه ، نه سوخت) با اندازه $P_R=g\rho V $ افزایش می یابد. و حداقل مقدار انرژی لازم برای وارد کردن موشک به مدار بدیهی است که با وزن آن افزایش می یابد:$ W_{min} = hP_R + W',$جایی که $W' $ کاری است که شما برای بلند کردن سوخت انجام می دهید. $W' $ در اینجا مهم نیست ، اما برای ثبت ، چیزی شبیه به زیر است:
$ W' = g\int_0^h m_{fuel}(z)dz'.$بنابراین ، اگر موشک خیلی کوچک باشد ، مقدار کمی از سوخت که می توانید در آن جای دهید ، انرژی کافی برای بلند کردن بدنه را ندارد. اگر موشک خیلی بزرگ است ، پس شما فقط انرژی را هدر می دهید زیرا غیرضروری سنگین است. این بدان معنی است که شما یک اندازه بهینه دارید که انرژی یک موشک تک مرحله ای را به حداقل می رساند. هنگامی که آن را پیدا کردید ، میزان سوخت مربوط به آن اندازه حداقل مورد نیاز برای انتقال موشک به مدار است.
اکنون موشکی در همان اندازه ، اما با 2 مرحله در نظر بگیرید. بیایید فرض کنیم که دارای یک موتور اضافی از وزن pe است. بیایید فرض کنیم که ، وقتی موشک شما به ارتفاع h / 2 رسید ، بیش از 1/3 مخزن آن خالی خواهد بود (که درست است). از آنجا که آن قسمت از مخزن من خالی است ، من ممکن است آن را پشت سر بگذارم (همراه با موتور) و وزن مرده را رها کنم (من آن را pt می نامم). اگر آن را در ساعت / 2 رها کنم انرژی لازم برای رسیدن به مدار خواهد بود
$W_{min2} = \frac{h}{2}(P_R + p_e) + \frac{h}{2}(P_R - p_t) + W'_2 = hP_R + W'_2 - \frac{h}{2}(p_t - p_e). $اگر به میزان قابل توجهی میزان سوخت اولیه را کاهش دهیم ، می توانیم $W'_2\leq W' $ تولید کنیم. بنابراین ، $ W_{min2}$ به وضوح کمتر از $W_{min} $ است ، به شرطی که موتوری که باید اضافه کنید سبکتر از مخزنی است که انداخته اید.4
ساده ترین راه برای فكر كردن در مورد آن این است ، تصور كنید تمام توده باقیمانده وقتی یك موشك 85٪ از سوخت خود را سوزانده است. جرم بیشتر مخزن و سازه در حال حاضر بیش از حد و ضایعات است. خوب است که بتوانیم آن جرم اضافی را جتیسون کنیم تا سوخت باقی مانده بتواند فقط محموله را تسریع کند.
این کاری است که یک موشک چند مرحله ای انجام می دهد. این جرم مراحل اولیه را جت می کند تا سوخت و رانش باقیمانده بتواند جرم بسیار کوچکتر را با سرعت بسیار بالاتری از آنچه می توانست اگر تنها یک مرحله وجود داشته باشد ، تسریع کند. به یاد داشته باشید شتاب متناسب با جرم است ، بنابراین اگر می توانید 80٪ از جرم خود را خلاص کنید ، می توانید بار حمل را 5 برابر بیشتر برای همان سوخت باقی مانده شتاب دهید.مزیت دیگر این است که شما می توانید از موتورهای موشکی استفاده کنید که برای سرعت های مختلف تنظیم شده اند. در مرحله اولیه شما به حداکثر رانش نیاز دارید و موشک به سرعت حرکت نمی کند. در مراحل بعدی شما موتورهای با کارایی بالا می خواهید ، نه لزوماً رانش بالا.
راکت می تواند یک موشک ، فضاپیما ، هواپیما یا وسیله نقلیه دیگری باشد که از موتور موشک رانش (یا فشار) می یابد
موشک های شیمیایی متداول ترین نوع موشک هستند و به طور معمول با احتراق پیشرانه موشک ، اگزوز خود را ایجاد می کنند. پیشرانه ها درون موشک حمل می شوند
موتورهای موشکی با عمل و واکنش کار می کنند. موتورهای موشکی موشک ها را به راحتی با پرتاب سریع اگزوز آنها به عقب سوق می دهند
موشک ها برای آتش بازی ، سلاح ، صندلی های پرتاب ، وسایل پرتاب برای ماهواره های مصنوعی ، پرواز فضایی انسان و اکتشافات فضایی استفاده می شوند
موشک ها ، چه به اندازه آتش بازی چه به اندازه وسایل پرتاب بزرگ ، با همان اصل عمل می کنند.
پوشش داده شده با یک سیستم محافظت حرارتی برای جلوگیری از حرارت اصطکاک هوا در هنگام پرواز و نگه داشتن در دمای سرد مورد نیاز برای برخی از سوخت ها و اکسید کننده ها
پره ها به بعضی از موشک های پایین قاب متصل می شوند تا ثبات را در حین پرواز فراهم کنند
-سیستم محموله
به ماموریت موشک بستگی دارد - مواد منفجره ، پرتاب ماهواره ، مسافران انسانی ، سیستم هدایت ممکن است شامل سنسورهای بسیار پیچیده ، کامپیوترهای روی صفحه ، رادارها و تجهیزات ارتباطی برای مانور موشک در پرواز باشد همچنین باید مقداری از ثبات را فراهم کند تا موشک در پرواز سقوط نکند
سیستم پیشرانه پیشرانه = سوخت + اکسید کننده انواع پیشرانه ها ،
سیستم های سوخت مایع ،سوخت و اکسید کننده از مخازن جداگانه به محفظه احتراق پمپ می شود
سیستم های پیشرانه جامد ،اینها سوخت و اکسید کننده را که از قبل با هم مخلوط شده اند ، در حالت جامد حمل می کنند
بخشهای مختلف موشک که در بالا توضیح داده شد بر اساس عملکرد به ساختار ، محموله ، سیستم هدایت و پیشرانه طبقه بندی شده اند. گروه بندی های احتمالی دیگری نیز وجود دارد.
به منظور تعیین وزن و عملکرد پرواز ، مهندسان غالباً محموله ، سازه ، ساختار پیشرانه (نازل ، پمپ ها ، مخازن و غیره) و راهنمایی ها را در یک پارامتر وزن خالی گروه بندی می کنند.
سپس وزن پیشرانه باقیمانده به تنها عاملی تبدیل می شود که با تعیین عملکرد موشک با زمان تغییر می کند.
انواع پیشرانه ها (ادامه) ،سیستم های پیشرانه گازسوز نوعی گاز فشرده را درگیر می کند
سیستم های پیشرانه ترکیبی معمولاً دارای یک سوخت جامد و یک اکسید کننده مایع یا گاز هستند
سیستم های پیشران ژل تحقیقی در مورد ژلینگ شدن پیشرانه های مایع برای دادن یک پیشرانه با فشار بخار کم برای کاهش خطر تصادفات انجام شده است.
سیستم های پیشرانه ژل مانند یک ماده سوخت جامد در ذخیره سازی و مانند یک پیشرانه مایع در حال استفاده رفتار می کند.
بخشهای مختلف موشک که در بالا توضیح داده شد بر اساس عملکرد به ساختار ، محموله ، سیستم هدایت و پیشرانه طبقه بندی شده اند. گروه بندی های احتمالی دیگری نیز وجود دارد.
به منظور تعیین وزن و عملکرد پرواز ، مهندسان غالباً محموله ، سازه ، ساختار پیشرانه (نازل ، پمپ ها ، مخازن و غیره) و راهنمایی ها را در یک پارامتر وزن خالی گروه بندی می کنند.
سپس وزن پیشرانه باقیمانده به تنها عاملی تبدیل می شود که با تعیین عملکرد موشک با زمان تغییر می کند.
یک وسیله نقلیه پرتابگر تصویر خوبی از قانون سوم حرکت نیوتن است ، "برای هر عملی ، یک واکنش برابر و مخالف وجود دارد." در مورد یک وسیله نقلیه پرتاب ، "عمل" عبارت است از جریان خروجی گازهای خروجی از عقب وسیله نقلیه حاصل از احتراق سوخت خودرو در موتور موشک آن ، و "واکنش" فشار است ، رانش نامیده می شود ، به ساختار داخلی وسیله نقلیه پرتاب اعمال می شود که آن را به سمت مخالف جریان خروجی سوق می دهد. برخلاف موتورهای جت ، که با همان اصل واکنش واکنش عمل می کنند اما اکسیژن مورد نیاز برای سوزاندن سوخت خود را از اتمسفر به دست می آورند ، موشک ها عامل اکسیداسیون خود را با خود حمل می کنند. به این ترتیب ، آنها می توانند در خلا فراتر از جو کار کنند.
هدف اصلی طراحان وسیله نقلیه پرتاب به حداکثر رساندن توانایی بلند کردن وسیله نقلیه در عین حال تأمین سطح اطمینان کافی با هزینه قابل قبول است. دستیابی به تعادل در بین این سه عامل چالش برانگیز است. برای اینکه خودروی پرتابگر از زمین بلند شود ، رانش به سمت بالا باید از وزن ترکیبی محموله فضاپیما ، پیشرانه های خودرو و ساختار آن بیشتر باشد. این امر باعث می شود که ساختار مکانیکی ، مخازن سوخت و موتورهای موشکی تا حد ممکن سبک اما به اندازه کافی قوی باشد تا بتواند در برابر نیروها و تنش های مرتبط با شتاب سریع از طریق جو مقاوم ، مقاومت کند. غالباً ، پیشرانه 80 درصد یا بیشتر از وزن كل ترکیب وسیله نقلیه و فضاپیمای پرتاب قبل از پرتاب را تشکیل می دهد.
یک وسیله نقلیه مخصوص پرتاب می تواند بسته به ماموریت و وزن فضاپیمای مورد نظر ، از چند طریق مختلف پیکربندی شود. این تنظیم مجدد را می توان با افزودن تعداد متفاوتی از تقویت کننده های تسمه ای ، معمولاً موتورهای راکتی جامد ، به مرحله اول خودرو یا با استفاده از مراحل مختلف بالایی انجام داد.
محافظت از بار
سفینه ای که وسیله نقلیه پرتابی به فضا حمل می کند تقریباً همیشه به قسمت بالای خودرو متصل است. در حین انتقال اتمسفر ، محموله با نوعی پرینت محافظت می شود که اغلب از مواد کامپوزیتی سبک ساخته می شود . هنگامی که وسیله پرتاب فراتر از متراکم ترین قسمت جو است ، این نمایشگاه از بین می رود. بعد از اینکه فضاپیما به سرعت اولیه مداری رسید، ممکن است برای شروع ماموریت خود ، از مرحله بالایی نهایی خودرو پرتاب جدا شود. متناوباً ، اگر قرار باشد فضاپیما به غیر از مدار کم زمین قرار بگیرد ، موتور موشکی مرحله بالا ممکن است برای مدتی خاموش شود زیرا بار فضاپیما در مدار قرار دارد. سپس موتور مجدداً راه اندازی می شود تا سرعت اضافی مورد نیاز برای انتقال محموله به مدار زمین بالاتر یا تزریق آن به مسیری كه آن را به اعماق فضا می برد ، منتقل شود.
پیمایش ، راهنمایی و کنترل
برای اینکه یک وسیله نقلیه بتواند یک فضاپیما را در مدار مورد نظر قرار دهد ، باید از قابلیت ناوبری ، هدایت و کنترل برخوردار باشد. جهت تعیین موقعیت ، سرعت و جهت گیری وسیله نقلیه در هر نقطه از مسیر حرکت به ناوبری نیاز است. همانطور که این متغیرها اندازه گیری می شوند ، سیستم هدایت وسیله نقلیه تعیین می کند که برای هدایت خودرو به سمت هدف مورد نظر چه اصلاحاتی لازم است. از سیستم های کنترلی برای اجرای دستورات راهنمایی از طریق حرکت موتورهای موشکی خودرو یا تغییر جهت رانش خودرو استفاده می شود. پیمایش ، راهنمایی و کنترل در بیشتر وسایل پرتاب با ترکیبی از نرم افزارهای پیچیده ، رایانه ها و سایر دستگاه های سخت افزاری حاصل می شود.
قابلیت اطمینان
یک وسیله پرتاب بنابراین تشکیل می شودیک یا چند موتور موشک ؛ سوخت برای موتورهایی که در مخازن سوخت حمل می شوند. سیستم های هدایت ، ناوبری و کنترل ؛ یک محموله و سازه ای که همه این عناصر را در خود جای داده است و ممکن است موتورهای اضافی برای افزایش بالابر به آن متصل شوند. همچنین پیوست های مختلفی بین وسیله نقلیه پرتابگر و صفحه پرتاب آن و ساختارهای مرتبط وجود دارد. یک وسیله نقلیه پرتاب مصرفی فقط یک فرصت برای انجام موفقیت آمیز مأموریت خود دارد ، بنابراین تمام عناصر آن باید دقیقاً و برای قابلیت اطمینان عملیاتی بسیار بالا طراحی و تولید شوند. همچنین ، همانطور که در بالا ذکر شد ، وسایل نقلیه پرتاب به گونه ای طراحی شده اند که تا حد ممکن سبک باشند تا بتوانند حداکثر قابلیت بالابری را داشته باشند. در نتیجه ، هر قسمت از یک وسیله نقلیه پرتاب در هنگام پرتاب نزدیک به نقطه شکست خود کار می کند ، زیرا خودرو تحت فشارهای ناشی از شتاب گرفتن از گذشته قرار می گیردسرعت صدا و انتقال جو و موتورهای موشکی آن تحت فشار ، دما ، شوک و لرزش کار می کنند.
نتیجه نهایی این است که پرتاب یک فضاپیما به فضای بیرونی کاری بسیار دشوار است و شکست های پرتاب یک واقعیت زندگی برای کسانی است که به دنبال دسترسی به فضا هستند. بسیاری از پرتاب های فضایی ، به ویژه آنهایی که فضاپیماهای تجاری را حمل می کنند ، در برابر خرابی بیمه می شوند ، زیرا غالباً سرمایه گذاری بیش از صد میلیون دلار است.
وسایل نقلیه پرتابی که مردم را به فضا منتقل می کنند "دارای رتبه انسانی" هستند. این به این معنی است که آنها از اجزای بالاترین قابلیت اطمینان استفاده می کنند ، در سیستم های حیاتی دارای افزونگی هستند ، قبل از پرتاب آزمایش بیشتری نسبت به وسایل نقلیه پرتاب کننده حامل یک فضاپیمای خودکار انجام می دهند و حاوی سیستم هایی هستند که در مورد مشکلات قریب الوقوع هشدار می دهند تا خدمه قادر به فرار از تصادف تنها یک خرابی یک وسیله نقلیه پرتاب در هنگام بلند شدن هواپیما بوده است که منجر به کشته شدن خدمه شده است این انفجار چلنجر در 28 ژانویه 1986 بود که باعث کشته شدن هر هفت فضانورد داخل هواپیما شد.پرتاب به فضا
اگرچه آنها در بسیاری از جزئیات برای وسایل نقلیه مختلف و پایگاههای مختلف پرتاب متفاوت هستند ، اما مراحل لازم برای آماده سازی یک وسیله نقلیه پرتابگر و میزان بار فضاپیمای آن برای پرتاب ، به طور کلی مشابه است.
اغلب اوقات ، مراحل مختلف و سایر عناصر یک وسیله نقلیه پرتاب به طور جداگانه ساخته می شوند و برای مونتاژ به پایگاه پرتاب حمل می شوند. آن مونتاژ می تواند در تاسیساتی دور از صفحه پرتاب یا در صفحه پرتاب واقع شود. مزیت ساختمان مونتاژ جداگانه این است که بسیاری از مراحل لازم برای آماده سازی خودرو برای پرتاب ، از جمله مونتاژ و سپس تسویه حساب یکپارچه ، در یک محیط بسته قابل انجام است . این همچنین بدان معنی است که صفحه پرتاب برای استفاده های دیگر در طول دوره مونتاژ و پرداخت در دسترس است.
مونتاژ وسایل نقلیه پرتاب یا به صورت عمودی یا افقی انجام می شود. مونتاژ عمودی به تاسیساتی به قدری بلند است که بتواند کل وسیله نقلیه و فضاپیما را در خود جای دهد . اجزای مختلف "انباشته" می شوند ، که از مرحله اول شروع می شوند و اغلب با اتصال فضاپیما به وسیله نقلیه پرتاب به پایان می رسند. (گاهی اوقات فضاپیما و وسیله نقلیه پرتابگر فقط در صفحه پرتاب جفت می شوند.) موتورهای راکت جامد تسمه ای ، اگر قرار است مورد استفاده قرار گیرند ، به مرحله اول هسته متصل می شوند. مونتاژ افقی به صورت انتها به انتها انجام می شود و نیازی به یک ساختمان بلند با دسترسی وسیله نقلیه در چند سطح ندارد. پس از مونتاژ ، تا آنجا که ممکن است آزمایش روی وسیله نقلیه یکپارچه انجام شود تا آمادگی آن برای پرتاب قبل از حمل و نقل به صفحه پرتاب بررسی شود.
هنگامی که به صفحه پرتاب رسید ، وسیله نقلیه به برج پرتاب متصل می شود ، که شامل اتصالات مختلف ناف و نقاط دسترسی است که برای تکمیل مراحل پرداخت و نظارت بر آمادگی نهایی خودرو برای پرتاب مورد نیاز است. اگر وسیله نقلیه به صورت افقی مونتاژ شده باشد ، باید با رسیدن به صفحه پرتاب به حالت عمودی درآید. غالباً صفحه پرتاب شامل نوعی سرپناه برای محافظت از وسیله نقلیه پرتابگر و فضاپیما از عناصر تا نزدیک به زمان پرتاب است و به تکنسین ها اجازه می دهد روند پرداخت را ادامه دهند. وسیله نقلیه پرتابی توسط نوعی وسیله اتصال دهنده روی بالشتک نگه داشته می شود.
اگر وسیله پرتاب روی صفحه پرتاب مونتاژ شود ، تمام مراحل فوق در آنجا انجام می شود. مونتاژ و پرداخت ممکن است چندین ماه طول بکشد و در این مدت صفحه پرتاب نمی تواند برای اهداف دیگر استفاده شود.
با نزدیک شدن به زمان پرتاب ، شمارش معکوس آغاز می شود. زمان شمارش معکوس می تواند از ساعاتی تا چند روز باشد. در هنگام شمارش معکوس ، مراحل نهایی مختلفی در زمان های مشخص انجام می شود تا خودرو برای پرتاب آماده شود. اگر وسیله نقلیه از پیشرانه های مایع استفاده کند ، پس از ذخیره شدن در مخازن نزدیک صفحه پرتاب ، آنها ساعاتی قبل از پرتاب بارگیری می شوند. نگهداری پیشرانه های برودتی در حالت مایع دشوار است. آنها تمایل به گاز شدن و "جوشاندن" وسیله نقلیه دارند. بنابراین ، آنها در مخازن سوخت خودرو تا حد امکان نزدیک به زمان پرتاب بارگیری می شوند و باید اطمینان حاصل شود که مخازن سوخت و اکسید کننده پر هستند. ساعاتی قبل از پرتاب برنامه ریزی شده ، سازه ای که از وسیله نقلیه محافظت کرده است از آن و برج پرتاب دور می شود.
پایگاه های راه اندازی باید به اطلاعات به روز آب و هوا دسترسی داشته باشند. معمولاً قوانینی از پیش تعیین شده در مورد شرایط آب و هوایی قابل قبول برای پرتاب فضایی وجود دارد ، از جمله وزش باد در محل پرتاب و از سطح بالا ، دید (برای نظارت بر وسیله نقلیه در چند دقیقه اول پرواز) و دما. این شرایط در سایتهای پرتاب و در وسایل نقلیه مختلف پرتاب متفاوت است. به عنوان مثال ، فضاپیمای خدمه ای از سایتهای روسی در شرایط بسیار جوی بسیار شدیدتر از آنچه برای پرتاب شاتل فضایی ایالات متحده از پایگاه پرتاب خود در فلوریدا قابل قبول است ، به فضا پرتاب می شود.
در چند دقیقه آخر شمارش معکوس ، بررسی نهایی انجام می شود تا اطمینان حاصل شود که وسیله نقلیه و فضاپیما برای پرتاب آماده هستند و سایر شرایط در وضعیت "رفتن" هستند. تمام اتصالات نافی بین برج پرتاب و خودرو جدا است. قبل از اینکه خودرو متعهد به پرتاب شود ، معمولاً موتورهای موشکی با سوخت مایع اجازه دارند چند ثانیه شلیک کنند. یک بررسی سریع رایانه ای انجام می شود و در صورت وجود نشانه هایی از مشکل ، موتورها می توانند خاموش شوند. پس از احتراق موتورهای راکتی جامد ، خودرو متعهد به پرتاب می شود. هنگامی که لحظه پرتاب فرا می رسد ، دستگاه هایی که وسیله نقلیه را به صفحه پرتاب نگه داشته اند ، به طور انفجاری جدا می شوند و وسیله نقلیه حرکت خود را آغاز می کند.
لانچ پد ها دارای ترانشه هایی برای انتقال شعله های خروجی از خودرو هستند و اغلب حجم زیادی از آب به شعله های آتش تزریق می شود. این کار برای به حداقل رساندن آسیب به وسیله نقلیه و صفحه پرتاب از گرما و ارتعاشات صوتی مرتبط با بلند شدن انجام می شه
موشکی که برای پرتاب ماهواره استفاده می شود "وسیله پرتاب ماهواره" نامیده می شود. یک وسیله نقلیه پرتاب از چندین بخش یا "مرحله" مختلف تشکیل شده است که هر مرحله نقش متفاوتی را بازی می کند.اولین مرحله از وسیله نقلیه پرتاب شامل سوختی است که برای بلند کردن ماهواره و پرتاب وسیله نقلیه از زمین و آسمان مورد نیاز است. این موشک ها باید بسیار قدرتمند باشند زیرا یک وسیله نقلیه پرتاب در هنگام صعود صدها تن وزن دارد. بعد از تمام شدن سوخت ، مرحله اول دیگر لازم نیست و خراب می شود و به زمین می افتد.
مرحله دوم شامل راکت های کوچکتری است که پس از پایان مرحله اول مشتعل می شوند. موشک های مرحله دوم مخازن سوخت خود را دارند. مرحله دوم برای ارسال ماهواره به فضا استفاده می شود. مانند مرحله اول ، بعد از تمام شدن سوخت و سوختن در جو زمین یا عقب افتادن ، آن خراب می شود.
مرحله بالایی وسیله پرتاب به ماهواره متصل می شود ، که در یک محافظ فلزی محصور شده است ، "فیرینگ" نامیده می شود. این نمایشگاه ماهواره را هنگام پرتاب محافظت می کند و حرکت وسیله پرتاب را از طریق مقاومت در برابر جو زمین آسان می کند. وقتی ماهواره بالاتر از جو زمین قرار گرفت و در جو زمین سوخت ، این نیروگاه از هم جدا می شود. موشک های مرحله فوقانی بعد از قرار گرفتن ماهواره در فضا شلیک می کنند و ماهواره را دقیقاً در مکان مورد نیاز قرار می دهند.
هنگامی که وسیله پرتاب از جو زمین خارج شد ، ماهواره از مرحله بالایی جدا می شود. سپس ماهواره به یک "مدار انتقال" فرستاده می شود که ماهواره را بالاتر به فضا می فرستد. ماهواره هنگامی که به ارتفاع مداری دلخواه خود می رسد ، صفحات خورشیدی و آنتن های ارتباطی خود را که در حین پرواز دور نگه داشته شده بود ، باز می کند. سپس ماهواره در مدار خود با ماهواره های دیگر قرار می گیرد
امروزه ، بسیاری از موشک ها بیش از یک ماهواره در مدار را حمل می کنند. اما چگونه یک موشک چند ماهواره را در مدار خود قرار می دهد؟
یک استراتژی نسبتاً رایج این است که دو یا چند ماهواره را روی هم جمع کنید. ماهواره بالایی مستقیماً در داخل تورینگ محموله قرار دارد . هر ماهواره دیگری که در زیر قرار دارد ، به نوعی یک پرده داخلی نشسته است. سیستم های پرتاب دوگانه نامیده می شوند .
بسته به نیاز ماهواره ها ، مرحله بالایی موشک می تواند چندین بار مشتعل شود با این حال ، 'شمع گذاری' ماهواره ها تنها روش نیست. ماهواره ها دقیقاً در کنار یکدیگر پرتاب می شوند و عملاً از یک آداپتور محموله مشترک استفاده می کنند. اگر ماهواره ها به گونه ای ساخته و طراحی شوند می توان این کار را انجام داد ،
این واقعاً به موشک و مأموریت و غیره بستگی دارد. اما به طور کلی همان موضوع مشترک صحبت می شود. فضاپیماها به طور معمول به موشک بارگیری می شوند و توسط نوعی پیچ و مهره انفجاری (یا گیره های دیگر) از نوع فناوری در جای خود نگه داشته می شوند. هنگامی که موشک آماده رها کردن فضاپیما باشد ، پیچ های انفجاری را فعال می کند و باعث می شود فضاپیما با سرعتی از موشک دور شود.
برای پرتاب یک موشک تک مرحله ای ، اندازه خاصی وجود دارد که انرژی مورد نیاز را به حداقل می رساند. وزن موشک شما (فقط بدنه ، نه سوخت) با اندازه $P_R=g\rho V $ افزایش می یابد. و حداقل مقدار انرژی لازم برای وارد کردن موشک به مدار بدیهی است که با وزن آن افزایش می یابد:$ W_{min} = hP_R + W',$جایی که $W' $ کاری است که شما برای بلند کردن سوخت انجام می دهید. $W' $ در اینجا مهم نیست ، اما برای ثبت ، چیزی شبیه به زیر است:
$ W' = g\int_0^h m_{fuel}(z)dz'.$بنابراین ، اگر موشک خیلی کوچک باشد ، مقدار کمی از سوخت که می توانید در آن جای دهید ، انرژی کافی برای بلند کردن بدنه را ندارد. اگر موشک خیلی بزرگ است ، پس شما فقط انرژی را هدر می دهید زیرا غیرضروری سنگین است. این بدان معنی است که شما یک اندازه بهینه دارید که انرژی یک موشک تک مرحله ای را به حداقل می رساند. هنگامی که آن را پیدا کردید ، میزان سوخت مربوط به آن اندازه حداقل مورد نیاز برای انتقال موشک به مدار است.
اکنون موشکی در همان اندازه ، اما با 2 مرحله در نظر بگیرید. بیایید فرض کنیم که دارای یک موتور اضافی از وزن pe است. بیایید فرض کنیم که ، وقتی موشک شما به ارتفاع h / 2 رسید ، بیش از 1/3 مخزن آن خالی خواهد بود (که درست است). از آنجا که آن قسمت از مخزن من خالی است ، من ممکن است آن را پشت سر بگذارم (همراه با موتور) و وزن مرده را رها کنم (من آن را pt می نامم). اگر آن را در ساعت / 2 رها کنم انرژی لازم برای رسیدن به مدار خواهد بود
$W_{min2} = \frac{h}{2}(P_R + p_e) + \frac{h}{2}(P_R - p_t) + W'_2 = hP_R + W'_2 - \frac{h}{2}(p_t - p_e). $اگر به میزان قابل توجهی میزان سوخت اولیه را کاهش دهیم ، می توانیم $W'_2\leq W' $ تولید کنیم. بنابراین ، $ W_{min2}$ به وضوح کمتر از $W_{min} $ است ، به شرطی که موتوری که باید اضافه کنید سبکتر از مخزنی است که انداخته اید.4
ساده ترین راه برای فكر كردن در مورد آن این است ، تصور كنید تمام توده باقیمانده وقتی یك موشك 85٪ از سوخت خود را سوزانده است. جرم بیشتر مخزن و سازه در حال حاضر بیش از حد و ضایعات است. خوب است که بتوانیم آن جرم اضافی را جتیسون کنیم تا سوخت باقی مانده بتواند فقط محموله را تسریع کند.
این کاری است که یک موشک چند مرحله ای انجام می دهد. این جرم مراحل اولیه را جت می کند تا سوخت و رانش باقیمانده بتواند جرم بسیار کوچکتر را با سرعت بسیار بالاتری از آنچه می توانست اگر تنها یک مرحله وجود داشته باشد ، تسریع کند. به یاد داشته باشید شتاب متناسب با جرم است ، بنابراین اگر می توانید 80٪ از جرم خود را خلاص کنید ، می توانید بار حمل را 5 برابر بیشتر برای همان سوخت باقی مانده شتاب دهید.مزیت دیگر این است که شما می توانید از موتورهای موشکی استفاده کنید که برای سرعت های مختلف تنظیم شده اند. در مرحله اولیه شما به حداکثر رانش نیاز دارید و موشک به سرعت حرکت نمی کند. در مراحل بعدی شما موتورهای با کارایی بالا می خواهید ، نه لزوماً رانش بالا.
راکت می تواند یک موشک ، فضاپیما ، هواپیما یا وسیله نقلیه دیگری باشد که از موتور موشک رانش (یا فشار) می یابد
موشک های شیمیایی متداول ترین نوع موشک هستند و به طور معمول با احتراق پیشرانه موشک ، اگزوز خود را ایجاد می کنند. پیشرانه ها درون موشک حمل می شوند
موتورهای موشکی با عمل و واکنش کار می کنند. موتورهای موشکی موشک ها را به راحتی با پرتاب سریع اگزوز آنها به عقب سوق می دهند
موشک ها برای آتش بازی ، سلاح ، صندلی های پرتاب ، وسایل پرتاب برای ماهواره های مصنوعی ، پرواز فضایی انسان و اکتشافات فضایی استفاده می شوند
موشک ها ، چه به اندازه آتش بازی چه به اندازه وسایل پرتاب بزرگ ، با همان اصل عمل می کنند.
پوشش داده شده با یک سیستم محافظت حرارتی برای جلوگیری از حرارت اصطکاک هوا در هنگام پرواز و نگه داشتن در دمای سرد مورد نیاز برای برخی از سوخت ها و اکسید کننده ها
پره ها به بعضی از موشک های پایین قاب متصل می شوند تا ثبات را در حین پرواز فراهم کنند
-سیستم محموله
به ماموریت موشک بستگی دارد - مواد منفجره ، پرتاب ماهواره ، مسافران انسانی ، سیستم هدایت ممکن است شامل سنسورهای بسیار پیچیده ، کامپیوترهای روی صفحه ، رادارها و تجهیزات ارتباطی برای مانور موشک در پرواز باشد همچنین باید مقداری از ثبات را فراهم کند تا موشک در پرواز سقوط نکند
سیستم پیشرانه پیشرانه = سوخت + اکسید کننده انواع پیشرانه ها ،
سیستم های سوخت مایع ،سوخت و اکسید کننده از مخازن جداگانه به محفظه احتراق پمپ می شود
سیستم های پیشرانه جامد ،اینها سوخت و اکسید کننده را که از قبل با هم مخلوط شده اند ، در حالت جامد حمل می کنند
بخشهای مختلف موشک که در بالا توضیح داده شد بر اساس عملکرد به ساختار ، محموله ، سیستم هدایت و پیشرانه طبقه بندی شده اند. گروه بندی های احتمالی دیگری نیز وجود دارد.
به منظور تعیین وزن و عملکرد پرواز ، مهندسان غالباً محموله ، سازه ، ساختار پیشرانه (نازل ، پمپ ها ، مخازن و غیره) و راهنمایی ها را در یک پارامتر وزن خالی گروه بندی می کنند.
سپس وزن پیشرانه باقیمانده به تنها عاملی تبدیل می شود که با تعیین عملکرد موشک با زمان تغییر می کند.
انواع پیشرانه ها (ادامه) ،سیستم های پیشرانه گازسوز نوعی گاز فشرده را درگیر می کند
سیستم های پیشرانه ترکیبی معمولاً دارای یک سوخت جامد و یک اکسید کننده مایع یا گاز هستند
سیستم های پیشران ژل تحقیقی در مورد ژلینگ شدن پیشرانه های مایع برای دادن یک پیشرانه با فشار بخار کم برای کاهش خطر تصادفات انجام شده است.
سیستم های پیشرانه ژل مانند یک ماده سوخت جامد در ذخیره سازی و مانند یک پیشرانه مایع در حال استفاده رفتار می کند.
بخشهای مختلف موشک که در بالا توضیح داده شد بر اساس عملکرد به ساختار ، محموله ، سیستم هدایت و پیشرانه طبقه بندی شده اند. گروه بندی های احتمالی دیگری نیز وجود دارد.
به منظور تعیین وزن و عملکرد پرواز ، مهندسان غالباً محموله ، سازه ، ساختار پیشرانه (نازل ، پمپ ها ، مخازن و غیره) و راهنمایی ها را در یک پارامتر وزن خالی گروه بندی می کنند.
سپس وزن پیشرانه باقیمانده به تنها عاملی تبدیل می شود که با تعیین عملکرد موشک با زمان تغییر می کند.
یک وسیله نقلیه پرتابگر تصویر خوبی از قانون سوم حرکت نیوتن است ، "برای هر عملی ، یک واکنش برابر و مخالف وجود دارد." در مورد یک وسیله نقلیه پرتاب ، "عمل" عبارت است از جریان خروجی گازهای خروجی از عقب وسیله نقلیه حاصل از احتراق سوخت خودرو در موتور موشک آن ، و "واکنش" فشار است ، رانش نامیده می شود ، به ساختار داخلی وسیله نقلیه پرتاب اعمال می شود که آن را به سمت مخالف جریان خروجی سوق می دهد. برخلاف موتورهای جت ، که با همان اصل واکنش واکنش عمل می کنند اما اکسیژن مورد نیاز برای سوزاندن سوخت خود را از اتمسفر به دست می آورند ، موشک ها عامل اکسیداسیون خود را با خود حمل می کنند. به این ترتیب ، آنها می توانند در خلا فراتر از جو کار کنند.
هدف اصلی طراحان وسیله نقلیه پرتاب به حداکثر رساندن توانایی بلند کردن وسیله نقلیه در عین حال تأمین سطح اطمینان کافی با هزینه قابل قبول است. دستیابی به تعادل در بین این سه عامل چالش برانگیز است. برای اینکه خودروی پرتابگر از زمین بلند شود ، رانش به سمت بالا باید از وزن ترکیبی محموله فضاپیما ، پیشرانه های خودرو و ساختار آن بیشتر باشد. این امر باعث می شود که ساختار مکانیکی ، مخازن سوخت و موتورهای موشکی تا حد ممکن سبک اما به اندازه کافی قوی باشد تا بتواند در برابر نیروها و تنش های مرتبط با شتاب سریع از طریق جو مقاوم ، مقاومت کند. غالباً ، پیشرانه 80 درصد یا بیشتر از وزن كل ترکیب وسیله نقلیه و فضاپیمای پرتاب قبل از پرتاب را تشکیل می دهد.
یک وسیله نقلیه مخصوص پرتاب می تواند بسته به ماموریت و وزن فضاپیمای مورد نظر ، از چند طریق مختلف پیکربندی شود. این تنظیم مجدد را می توان با افزودن تعداد متفاوتی از تقویت کننده های تسمه ای ، معمولاً موتورهای راکتی جامد ، به مرحله اول خودرو یا با استفاده از مراحل مختلف بالایی انجام داد.
محافظت از بار
سفینه ای که وسیله نقلیه پرتابی به فضا حمل می کند تقریباً همیشه به قسمت بالای خودرو متصل است. در حین انتقال اتمسفر ، محموله با نوعی پرینت محافظت می شود که اغلب از مواد کامپوزیتی سبک ساخته می شود . هنگامی که وسیله پرتاب فراتر از متراکم ترین قسمت جو است ، این نمایشگاه از بین می رود. بعد از اینکه فضاپیما به سرعت اولیه مداری رسید، ممکن است برای شروع ماموریت خود ، از مرحله بالایی نهایی خودرو پرتاب جدا شود. متناوباً ، اگر قرار باشد فضاپیما به غیر از مدار کم زمین قرار بگیرد ، موتور موشکی مرحله بالا ممکن است برای مدتی خاموش شود زیرا بار فضاپیما در مدار قرار دارد. سپس موتور مجدداً راه اندازی می شود تا سرعت اضافی مورد نیاز برای انتقال محموله به مدار زمین بالاتر یا تزریق آن به مسیری كه آن را به اعماق فضا می برد ، منتقل شود.
پیمایش ، راهنمایی و کنترل
برای اینکه یک وسیله نقلیه بتواند یک فضاپیما را در مدار مورد نظر قرار دهد ، باید از قابلیت ناوبری ، هدایت و کنترل برخوردار باشد. جهت تعیین موقعیت ، سرعت و جهت گیری وسیله نقلیه در هر نقطه از مسیر حرکت به ناوبری نیاز است. همانطور که این متغیرها اندازه گیری می شوند ، سیستم هدایت وسیله نقلیه تعیین می کند که برای هدایت خودرو به سمت هدف مورد نظر چه اصلاحاتی لازم است. از سیستم های کنترلی برای اجرای دستورات راهنمایی از طریق حرکت موتورهای موشکی خودرو یا تغییر جهت رانش خودرو استفاده می شود. پیمایش ، راهنمایی و کنترل در بیشتر وسایل پرتاب با ترکیبی از نرم افزارهای پیچیده ، رایانه ها و سایر دستگاه های سخت افزاری حاصل می شود.
قابلیت اطمینان
یک وسیله پرتاب بنابراین تشکیل می شودیک یا چند موتور موشک ؛ سوخت برای موتورهایی که در مخازن سوخت حمل می شوند. سیستم های هدایت ، ناوبری و کنترل ؛ یک محموله و سازه ای که همه این عناصر را در خود جای داده است و ممکن است موتورهای اضافی برای افزایش بالابر به آن متصل شوند. همچنین پیوست های مختلفی بین وسیله نقلیه پرتابگر و صفحه پرتاب آن و ساختارهای مرتبط وجود دارد. یک وسیله نقلیه پرتاب مصرفی فقط یک فرصت برای انجام موفقیت آمیز مأموریت خود دارد ، بنابراین تمام عناصر آن باید دقیقاً و برای قابلیت اطمینان عملیاتی بسیار بالا طراحی و تولید شوند. همچنین ، همانطور که در بالا ذکر شد ، وسایل نقلیه پرتاب به گونه ای طراحی شده اند که تا حد ممکن سبک باشند تا بتوانند حداکثر قابلیت بالابری را داشته باشند. در نتیجه ، هر قسمت از یک وسیله نقلیه پرتاب در هنگام پرتاب نزدیک به نقطه شکست خود کار می کند ، زیرا خودرو تحت فشارهای ناشی از شتاب گرفتن از گذشته قرار می گیردسرعت صدا و انتقال جو و موتورهای موشکی آن تحت فشار ، دما ، شوک و لرزش کار می کنند.
نتیجه نهایی این است که پرتاب یک فضاپیما به فضای بیرونی کاری بسیار دشوار است و شکست های پرتاب یک واقعیت زندگی برای کسانی است که به دنبال دسترسی به فضا هستند. بسیاری از پرتاب های فضایی ، به ویژه آنهایی که فضاپیماهای تجاری را حمل می کنند ، در برابر خرابی بیمه می شوند ، زیرا غالباً سرمایه گذاری بیش از صد میلیون دلار است.
وسایل نقلیه پرتابی که مردم را به فضا منتقل می کنند "دارای رتبه انسانی" هستند. این به این معنی است که آنها از اجزای بالاترین قابلیت اطمینان استفاده می کنند ، در سیستم های حیاتی دارای افزونگی هستند ، قبل از پرتاب آزمایش بیشتری نسبت به وسایل نقلیه پرتاب کننده حامل یک فضاپیمای خودکار انجام می دهند و حاوی سیستم هایی هستند که در مورد مشکلات قریب الوقوع هشدار می دهند تا خدمه قادر به فرار از تصادف تنها یک خرابی یک وسیله نقلیه پرتاب در هنگام بلند شدن هواپیما بوده است که منجر به کشته شدن خدمه شده است این انفجار چلنجر در 28 ژانویه 1986 بود که باعث کشته شدن هر هفت فضانورد داخل هواپیما شد.پرتاب به فضا
اگرچه آنها در بسیاری از جزئیات برای وسایل نقلیه مختلف و پایگاههای مختلف پرتاب متفاوت هستند ، اما مراحل لازم برای آماده سازی یک وسیله نقلیه پرتابگر و میزان بار فضاپیمای آن برای پرتاب ، به طور کلی مشابه است.
اغلب اوقات ، مراحل مختلف و سایر عناصر یک وسیله نقلیه پرتاب به طور جداگانه ساخته می شوند و برای مونتاژ به پایگاه پرتاب حمل می شوند. آن مونتاژ می تواند در تاسیساتی دور از صفحه پرتاب یا در صفحه پرتاب واقع شود. مزیت ساختمان مونتاژ جداگانه این است که بسیاری از مراحل لازم برای آماده سازی خودرو برای پرتاب ، از جمله مونتاژ و سپس تسویه حساب یکپارچه ، در یک محیط بسته قابل انجام است . این همچنین بدان معنی است که صفحه پرتاب برای استفاده های دیگر در طول دوره مونتاژ و پرداخت در دسترس است.
مونتاژ وسایل نقلیه پرتاب یا به صورت عمودی یا افقی انجام می شود. مونتاژ عمودی به تاسیساتی به قدری بلند است که بتواند کل وسیله نقلیه و فضاپیما را در خود جای دهد . اجزای مختلف "انباشته" می شوند ، که از مرحله اول شروع می شوند و اغلب با اتصال فضاپیما به وسیله نقلیه پرتاب به پایان می رسند. (گاهی اوقات فضاپیما و وسیله نقلیه پرتابگر فقط در صفحه پرتاب جفت می شوند.) موتورهای راکت جامد تسمه ای ، اگر قرار است مورد استفاده قرار گیرند ، به مرحله اول هسته متصل می شوند. مونتاژ افقی به صورت انتها به انتها انجام می شود و نیازی به یک ساختمان بلند با دسترسی وسیله نقلیه در چند سطح ندارد. پس از مونتاژ ، تا آنجا که ممکن است آزمایش روی وسیله نقلیه یکپارچه انجام شود تا آمادگی آن برای پرتاب قبل از حمل و نقل به صفحه پرتاب بررسی شود.
هنگامی که به صفحه پرتاب رسید ، وسیله نقلیه به برج پرتاب متصل می شود ، که شامل اتصالات مختلف ناف و نقاط دسترسی است که برای تکمیل مراحل پرداخت و نظارت بر آمادگی نهایی خودرو برای پرتاب مورد نیاز است. اگر وسیله نقلیه به صورت افقی مونتاژ شده باشد ، باید با رسیدن به صفحه پرتاب به حالت عمودی درآید. غالباً صفحه پرتاب شامل نوعی سرپناه برای محافظت از وسیله نقلیه پرتابگر و فضاپیما از عناصر تا نزدیک به زمان پرتاب است و به تکنسین ها اجازه می دهد روند پرداخت را ادامه دهند. وسیله نقلیه پرتابی توسط نوعی وسیله اتصال دهنده روی بالشتک نگه داشته می شود.
اگر وسیله پرتاب روی صفحه پرتاب مونتاژ شود ، تمام مراحل فوق در آنجا انجام می شود. مونتاژ و پرداخت ممکن است چندین ماه طول بکشد و در این مدت صفحه پرتاب نمی تواند برای اهداف دیگر استفاده شود.
با نزدیک شدن به زمان پرتاب ، شمارش معکوس آغاز می شود. زمان شمارش معکوس می تواند از ساعاتی تا چند روز باشد. در هنگام شمارش معکوس ، مراحل نهایی مختلفی در زمان های مشخص انجام می شود تا خودرو برای پرتاب آماده شود. اگر وسیله نقلیه از پیشرانه های مایع استفاده کند ، پس از ذخیره شدن در مخازن نزدیک صفحه پرتاب ، آنها ساعاتی قبل از پرتاب بارگیری می شوند. نگهداری پیشرانه های برودتی در حالت مایع دشوار است. آنها تمایل به گاز شدن و "جوشاندن" وسیله نقلیه دارند. بنابراین ، آنها در مخازن سوخت خودرو تا حد امکان نزدیک به زمان پرتاب بارگیری می شوند و باید اطمینان حاصل شود که مخازن سوخت و اکسید کننده پر هستند. ساعاتی قبل از پرتاب برنامه ریزی شده ، سازه ای که از وسیله نقلیه محافظت کرده است از آن و برج پرتاب دور می شود.
پایگاه های راه اندازی باید به اطلاعات به روز آب و هوا دسترسی داشته باشند. معمولاً قوانینی از پیش تعیین شده در مورد شرایط آب و هوایی قابل قبول برای پرتاب فضایی وجود دارد ، از جمله وزش باد در محل پرتاب و از سطح بالا ، دید (برای نظارت بر وسیله نقلیه در چند دقیقه اول پرواز) و دما. این شرایط در سایتهای پرتاب و در وسایل نقلیه مختلف پرتاب متفاوت است. به عنوان مثال ، فضاپیمای خدمه ای از سایتهای روسی در شرایط بسیار جوی بسیار شدیدتر از آنچه برای پرتاب شاتل فضایی ایالات متحده از پایگاه پرتاب خود در فلوریدا قابل قبول است ، به فضا پرتاب می شود.
در چند دقیقه آخر شمارش معکوس ، بررسی نهایی انجام می شود تا اطمینان حاصل شود که وسیله نقلیه و فضاپیما برای پرتاب آماده هستند و سایر شرایط در وضعیت "رفتن" هستند. تمام اتصالات نافی بین برج پرتاب و خودرو جدا است. قبل از اینکه خودرو متعهد به پرتاب شود ، معمولاً موتورهای موشکی با سوخت مایع اجازه دارند چند ثانیه شلیک کنند. یک بررسی سریع رایانه ای انجام می شود و در صورت وجود نشانه هایی از مشکل ، موتورها می توانند خاموش شوند. پس از احتراق موتورهای راکتی جامد ، خودرو متعهد به پرتاب می شود. هنگامی که لحظه پرتاب فرا می رسد ، دستگاه هایی که وسیله نقلیه را به صفحه پرتاب نگه داشته اند ، به طور انفجاری جدا می شوند و وسیله نقلیه حرکت خود را آغاز می کند.
لانچ پد ها دارای ترانشه هایی برای انتقال شعله های خروجی از خودرو هستند و اغلب حجم زیادی از آب به شعله های آتش تزریق می شود. این کار برای به حداقل رساندن آسیب به وسیله نقلیه و صفحه پرتاب از گرما و ارتعاشات صوتی مرتبط با بلند شدن انجام می شه

- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: هوافضا
تغریف اکورد بال وتر ایرفویل
وتر ایرفویل خطی است که لبه حمله و لبه فرار آن را به یکدیگر متصل میکند. در واقع این عبارت، فاصله مستقیم بین لبه حمله و لبه فرار ایرفویلها را نشان میدهد. این طول کاربرد بسیار زیادی در توربوماشینها و علم هوافضا دارد. برای مثال در این مسائل از طول وتر ایرفویل برای تعریف عدد رینولدز به شکل زیر استفاده میشود.
در این رابطهLطول وتر ایرفویل را نشان میدهد و ρ ،V و μ نیز به ترتیب نمایش دهنده سرعت جریان ورودی، چگالی و ویسکوزیته هستند $ Re = ρ v L / μ$
سر خط کشش از لبه بال به موازات لبه فرار به مرکزی است.
تغییرات مختلفی برای توصیف آکورد کل بال وجود دارد
میانگین آیرودینامیک وتر
به عنوان تعریف با مختصات در امتداد بال و وتر در . برای بال های جارو شده یا دلتا این وتر معادل بال مستطیل را می دهد و برای قرار دادن مرکز ثقل برای پایداری مهم است.
نسبت ابعاد ، نسبت مبتنی بر دهانه و وتر بالهای هواپیما است. طول طول بال به بال اندازه گیری های نوک بال است. وتر از 'عمق' بال از لبه به لبه فرار، اندازه گیری در یک خط مستقیم است.
از آنجا که تعداد بسیار کمی از هواپیماها دارای فرم وتر ثابت هستند ، این امر برای محاسبه به فرمولی بسیار زیبا احتیاج دارد ، بنابراین ما می توانیم به طور موثر وتر را متوسط کنیم:$ AR=\frac{b^2}{S}$
AR= نسبت ابعاد B= بالهای بال S= مساحت بال
$\frac2 S \int_0^{\frac b 2} c(y)^2 dy$ ، نسبت ابعاد بر اساس نقش یا نیاز هواپیما انتخاب می شود. نیاز به چابکی ، و همچنین نیاز به فشردگی ، نسبت ابعادی کم را القا می کند. در هر دو مورد ، هواپیماهای جنگنده و هواپیماهای بوش از چابکی و اندازه کوچک بهره مند می شوند. نسبتهای ابعادی بالا کارایی کروز بسیار خوبی را ارائه می دهند اما می توانند از ویژگیهای فرود ضعیف باشند (کشیدن زیاد در سرعتهای پایین یا زاویه حمله بالا به دلیل وجود ناحیه فرونتال) که غالباً توسط دستگاههای بالابرنده مانند فلپ و لتها جبران می شوند.
نسبت ابعاد یک بال باعث تغییر در کشش ناشی از آن نمی شود. افزایش دهانه
ضریب درگ ناشی از یک جناح ، و این به نظر می رسد نشان می دهد که نسبت بزرگتر AR به کشیدن ناشی از کاهش ضریب . اما فقط در همان ضریب بالابر$c_{Droham} = \frac{c_L^2}{\pi\cdot AR\cdot\epsilon} $
حال بیایید به اعداد واقعی نگاه کنیم و دو بال یک بازه ، اما نسبت های متفاوت را با هم مقایسه کنیم. برای سادگی ، بال 1 دارای AR 5 و بال 2 دارای AR 10 است. بیایید فرض کنیم که هر دو بال جرم یکسانی دارند. از آنجا که دامنه هر دو بال یکسان است ، بال 1 دو برابر بال بال دارد. برای ایجاد بالابر یکسان ، بال 1 فقط به نیمی از بالابر در هر منطقه نسبت به بال 2 نیاز دارد! این بدان معناست که آن فقط نیمی از بال 2 است و اکنون اجازه می دهد دوباره کشش ناشی از آن را بررسی کنیم:$D_roham = q_\infty\cdot S\cdot c_{Di} $
بال 1$ D_{roham_1} = q_\infty\cdot S_1\cdot\frac{c_{L_1}^2}{\pi\cdot AR_1\cdot\epsilon}$
بال 2: $ D_{roham_2} = q_\infty\cdot S_2\cdot\frac{c_{L_2}^2}{\pi\cdot AR_2\cdot\epsilon} = q_\infty\cdot 0.5\cdot S_1\cdot\frac{4\cdot c_{L_1}^2}{\pi\cdot 2\cdot AR_1\cdot\epsilon} = D_{i_1}$
من دانشجوی جدید هواپیمایی هستم و روز دیگر در مورد کشش القایی می خواندم. من می دانم که در نتیجه گرداب های نوک تولید می شود و هرچه نسبت ابعاد هواپیما بیشتر باشد ، نیروی کشش ناشی از آن کمتر است. اما وقتی که به معادله نیرو رسید ، برابر است با:$D_i = \frac{1}{2}\rho V^2 S \frac{C_L^2}{\pi AR \epsilon} $اگر نسبت ابعاد AR را با$\frac{b}{c} $ جایگزین کنیم و منطقه S را bc قرار دهیم ، مدت دهانه لغو می شود و کشش ناشی از آن فقط تحت تأثیر وتر قرار می گیرد.نسبت AR می تواند به عنوان $\frac{b}{c}$ نوشته شود که برابر با $\frac{b^2}{S} $ است.
قبل از شروع به تعویض ، توجه داشته باشید که CL به سطح بال بال S نیز بستگی دارد.$L = \frac{1}{2}\rho V^2 C_L S $جایگزینی همه اینها در بازده فرمول کششی:$ D_i = \frac{1}{2}\rho V^2 S \frac{C_L^2}{\pi AR \epsilon} =
\frac{L^2}{\frac{1}{2}\rho V^2 S \pi AR \epsilon} = \frac{L^2}{\frac{1}{2}\rho V^2 \pi b^2 \epsilon}$
این به نوعی با نسبت نسبت بر نیروی کشش ناشی از آن تناقض دارد ، نه؟
اگر هر دو بازده یکسانی داشته باشند ، کشش القایی هر دو در یک بالابر یکسان است. برای کاهش کشش ناشی از آن ، بدون توجه به نسبت ابعاد ، به افزایش دامنه نیاز دارید.ϵ
با این حال ، یک بال نسبت بالاتر دارای مزایایی است:
سطح سطح پایین به معنای کشش اصطکاک کمتر است
سطح پایین تر نیز به معنی جرم کمتری است ، حداقل در نسبت های نسبت متوسط.
لحظه های کوچک تر صدا کردن ، نیاز به هواپیمای دم کوچکتر
اول ساختاری است. نیروهای خمشی مرتبط با بالهای بسیار خوب بسیار افراطی هستند و مواد مورد نیاز کاملاً در فضا قرار دارند. برای نمونه هایی از این موارد ، از گلایدرهای با عملکرد بالا یا در انتهای دیوانه ، هواپیماهای خورشیدی یا مجهز به انسان دیدن کنید. انجام این کار در اندازه هواپیمای مسافربری فقط سخت است.
دلیل دوم عملی تر است: . بال با نسبت ابعاد فوق العاده نسبت به بقیه هواپیماها یک فضا را اشغال می کند.
اگر آکورد را افزایش دهید ، بالابر تقریباً به صورت خطی بالا می رود و پایداری کاهش می یابد ، زیرا اکنون نیروی بال بال دارای بازوی اهرم بلندتری در جهت جریان است. با افزایش آکورد ، نسبت ابعاد را کاهش می دهید ...چند نکته وجود دارد که من نمی فهمم ، اما من فکر می کنم آنها احتمالاً کاملاً به هم ربط دارند ، بنابراین من قصد دارم با هم از آنها بپرسم.
اولاً ، نسبت ابعاد بال چیست؟ آیا این اشاره به میزان بروز بال است و اینکه چگونه یک بال بلندتر به معنای آن است که درصد بیشتری از بدنه بدنه توسط بال پوشانده شده است (همانطور که از جلو دیده می شود)؟ یا من دور از علامت هستم؟ثانیا چرا افزایش طول وتر باعث کاهش پایداری بال می شود؟ به نظر من بال طولانی تر به معنای پایدارتر بودن صنعت است زیرا جریان هوا برای مدت طولانی تری مجبور به خط می شود.
در آخر ، این همه مربوط به نحوه در نظر گرفتن طول وتر در هنگام طراحی بال است. آیا فاکتورهای دیگری با محوریت آکورد وجود دارد که باید هنگام طراحی بال در نظر گرفته شود؟
در طول طراحی ، طول وتر نتیجه دهانه بال و مساحت بال خواهد بود ، زیرا این دو مورد همان چیزی است که طراح می خواهد تنظیم کند. به عبارت دقیق تر ، او سعی می کند بارگذاری بال مشخصی را تنظیم کند ، تلاش می کند تا مساحت (و وزن) بال را به حداقل برساند به طوری که بال در همه موارد طراحی ، فقط به اندازه کافی بالابر برای جرم هواپیما ایجاد کند. برخاست ، حداکثر ارتفاع و حداقل شعاع چرخش کلاسیک هایی است که حداقل مساحت بال را هدایت می کند.
اکنون روی نسبت ابعاد تمرکز خواهم کرد . هرچه نسبت ابعاد بیشتر باشد ، نوک بال کمتر بر جریان هوا در اطراف بال تأثیر می گذارد. این به این معنی است که بال برای یک زاویه حمله مشخص ، بلند کردن بیشتری ایجاد می کند ، اما همچنین زاویه اصطکاک ایستادن ، پایین تر است. نسبت دهانه بال به جرم هواپیما (که بارگذاری دهانه نامیده می شود) نیروی محرکه کشش القایی است. با این حال ، دامنه و نسبت ابعاد نیز باعث ایجاد جرم ساختاری بال می شود ، بنابراین شما باید یک سازش صحیح بین کشش ناشی از کم و جرم کم بال پیدا کنید.کشش القایی چیست؟ این نتیجه ایجاد لیفت در یک بازه محدود است. بال با انحراف هوا به سمت پایین باعث ایجاد لیفت می شود. این به تدریج بر روی آکورد بال اتفاق می افتد ، و یک نیروی واکنش را به صورت متعامد نسبت به سرعت محلی هوا ایجاد می کند. این بدان معنی است که نیروی واکنش به سمت بالا و کمی به عقب نشان داده شده است. این مولفه رو به عقب کشش القایی است! بال هرچه عرض بیشتری داشته باشد ، می توان از هوا بیشتری برای ایجاد بالابر استفاده کرد ، بنابراین به انحراف کمتری نیاز است. در نتیجه ، شیب عقب نیروی واکنش کوچکتر است و در نتیجه کشش کمتری برای همان بالابر ایجاد می شود.
اگر سریع پرواز کنید ، توده هوا زیادی در واحد زمان از کنار بال جریان دارد ، بنابراین باید هوا را فقط کمی منحرف کنید. درگ ناشی از شما کم است. به همین دلیل است که کشش القایی با سرعت هوا معکوس تغییر می کند.
اکنون می دانید که برای سرعت بالا در چگالی زیاد ، کشش ناشی از آن مهم نیست. اگر هواپیمای تهاجمی را طراحی کنید که باید در ارتفاع کم پرواز کند ، نسبت ابعادی کم به شما کمک می کند: افزایش بالابر به دلیل برخورد با هوا ، نسبت به بال با نسبت ابعاد بالا ، کوچکتر است و کشش ناشی از آن قابل کنترل است.
تغییرات شیب منحنی بالابر با نسبت ابعاد در جریان صوت در نمودار ساده زیر نشان داده شده است. برای یک بدن باریک (نسبت ابعاد ≈ 0) ، شیب ضریب بالابر cL در زاویه حمله $c_{L\alpha} = \frac{\pi \cdot AR}{2} $ است. لطفا توجه داشته باشید که خط قرمز فقط برای AR = 0 معتبر است! سپس شیب منحنی لیفت تا$c_{L\alpha} = 2\cdot\pi $ برای $ AR = \infty$ افزایش می یابد (و ضخامت ورق هوا صفر و بدون اثر اصطکاک) ، همانطور که توسط خط آبی نشان داده شده است.$AR=\frac{b^2}{S} $در اینجا b دهانه بال است و S منطقه بال است. برای بال مستطیلی که همان دهانه تا وتر است. با استفاده از ناحیه در مراحل جانبی تعریف ، نیاز به تعریف وتر متوسط برای اشکال پیچیده تر بال است.
برخی از خصوصیات بال به مساحت آن بستگی دارد در حالی که سایر موارد به دهانه بستگی دارد:
آسانسور متناسب با مساحت و مربع سرعت مشخص شده (فشار دینامیکی) است.
کشش القایی با دهانه معکوس و با سرعت نشان داده شده معکوس است.
کشیدن فرم متناسب با دهانه ، ضخامت و مربع سرعت مشخص شده است.
کشیدن پوست متناسب با مساحت و مربع سرعت مشخص شده است.
کشش موج متناسب با دهانه ، ضخامت و به سرعت بالاتر از تعداد واگرایی کشش است.
قدرت با دهانه متناسب عکس است. زاویه حمله $F = C_L\rho U^2S\sin({\alpha + \beta}) $
برای هر بال سرعت (مشخص شده) وجود دارد که بال در آن کارآمدتر است زیرا کشش القا شده در حال حاضر کاهش یافته و سایر اشکال کشش هنوز خیلی بزرگ نشده اند.
از آنجا که کشش القایی با دهانه کاهش می یابد ، بالهای با نسبت ابعاد بالا در سرعتهای پایین نقطه بهینه دارند و کشش کلی آنها در این سرعت به طور کلی کمتر است. به همین دلیل گلایدرها دارای بالهایی با نسبت ابعاد بسیار بالا (بسیار بلند) هستند. همانطور که سایر اشکال کشش با دهانه افزایش می یابد ، برای سرعت های بالاتر ، به خصوص مافوق صوت ، نسبت ابعاد پایین تر بهتر است.
توجه داشته باشید که تمام سرعتها سرعت نشان داده شده است. سرعت نشان داده شده فشار دینامیکی است که با سرعتی که در سطح دریا اتفاق می افتد بیان می شود. اما با کاهش چگالی با ارتفاع ، سرعت نشان داده شده نیز کاهش می یابد. بنابراین جت های حمل و نقل با سرعت متوسط نشان می دهند و می توانند بالهای نسبت ابعادی بالایی داشته باشند. $F = \frac{1}{2}Ac_a\rho v^2 $ و$A = w l \sin(\alpha\frac{\pi}{180}) $
رابطه ضریب درگ و لیفت $ C_D = C_{D_{min}} + \frac{{C_L}^2}{\pi \cdot AR \cdot e}$ وفتی $L = C_L \cdot \frac{\rho}{2} \cdot v^2 \cdot A $ و برای درگ $D = C_D \cdot \frac{\rho}{2} \cdot v^2 \cdot A $ برای پرواز باید 1
اگر وحدت نیروها پرواز هواپیما را برای شما کنترل می کند ، پس باید هر نیرو را در نقطه هواپیمایی که تولید می شود ، اعمال کنید. به عنوان مثال برای بال های خود ، نیروی بالابری هر بال را در مرکز جرم آن بال اعمال کنید. نیرو را در مرکز جرم کل هواپیما وارد نکنید. به این دلیل که وحدت فقط می تواند گشتاور صحیح را از این طریق محاسبه کند.$ \sum{F}_x=m\,a=F-R-W\tag 1$ رانش و همچنین $ \sum{F}_y=N+A-m\,g=0\tag 2$
و داریم $R=\mu\,N $و $ W=\frac{1}{2}c_W\,\rho\,S\,v^2$ و لیفت هم $ A=\frac{1}{2}c_A\,\rho\,S\,v^2$ خوب داریم $N=m\,g-A=m\,g-\frac{1}{2}c_A\,\rho\,S\,v^2 $ ومن n=0 دارم$v_S^2=\frac{2m\,g}{c_{AS}\,\rho\,S} $ با توجه به روابط اول دارم $m\,a=F-R-W=F-\mu\left(m\,g-\frac{1}{2}c_A\,\rho\,S\,v^2\right)
-\frac{1}{2}c_W\,\rho\,S\,v^2 $ توجه کنید من به رابطه $a(v)=\frac{c_R\,\rho\,S}{2m}\left(\underbrace{2\frac{F-\mu\,m\,g}{c_R\,\rho\,S}}_{v_E^2}-v^2\right) $ با توجه $c_R=c_W-\mu\,c_A $ رسیدمپس برای تیک اف من به فاصله $ roham_S=\int_{0}^{v_S}\,\frac{v\,dv}{a(v)}=-\frac{m}{c_R\,\rho\,S}\ln\left(1-\frac{v_S^2}{v_E^2}\right)$ نیاز دارم
وتر ایرفویل خطی است که لبه حمله و لبه فرار آن را به یکدیگر متصل میکند. در واقع این عبارت، فاصله مستقیم بین لبه حمله و لبه فرار ایرفویلها را نشان میدهد. این طول کاربرد بسیار زیادی در توربوماشینها و علم هوافضا دارد. برای مثال در این مسائل از طول وتر ایرفویل برای تعریف عدد رینولدز به شکل زیر استفاده میشود.
در این رابطهLطول وتر ایرفویل را نشان میدهد و ρ ،V و μ نیز به ترتیب نمایش دهنده سرعت جریان ورودی، چگالی و ویسکوزیته هستند $ Re = ρ v L / μ$
سر خط کشش از لبه بال به موازات لبه فرار به مرکزی است.
تغییرات مختلفی برای توصیف آکورد کل بال وجود دارد
میانگین آیرودینامیک وتر
به عنوان تعریف با مختصات در امتداد بال و وتر در . برای بال های جارو شده یا دلتا این وتر معادل بال مستطیل را می دهد و برای قرار دادن مرکز ثقل برای پایداری مهم است.
نسبت ابعاد ، نسبت مبتنی بر دهانه و وتر بالهای هواپیما است. طول طول بال به بال اندازه گیری های نوک بال است. وتر از 'عمق' بال از لبه به لبه فرار، اندازه گیری در یک خط مستقیم است.
از آنجا که تعداد بسیار کمی از هواپیماها دارای فرم وتر ثابت هستند ، این امر برای محاسبه به فرمولی بسیار زیبا احتیاج دارد ، بنابراین ما می توانیم به طور موثر وتر را متوسط کنیم:$ AR=\frac{b^2}{S}$
AR= نسبت ابعاد B= بالهای بال S= مساحت بال
$\frac2 S \int_0^{\frac b 2} c(y)^2 dy$ ، نسبت ابعاد بر اساس نقش یا نیاز هواپیما انتخاب می شود. نیاز به چابکی ، و همچنین نیاز به فشردگی ، نسبت ابعادی کم را القا می کند. در هر دو مورد ، هواپیماهای جنگنده و هواپیماهای بوش از چابکی و اندازه کوچک بهره مند می شوند. نسبتهای ابعادی بالا کارایی کروز بسیار خوبی را ارائه می دهند اما می توانند از ویژگیهای فرود ضعیف باشند (کشیدن زیاد در سرعتهای پایین یا زاویه حمله بالا به دلیل وجود ناحیه فرونتال) که غالباً توسط دستگاههای بالابرنده مانند فلپ و لتها جبران می شوند.
نسبت ابعاد یک بال باعث تغییر در کشش ناشی از آن نمی شود. افزایش دهانه
ضریب درگ ناشی از یک جناح ، و این به نظر می رسد نشان می دهد که نسبت بزرگتر AR به کشیدن ناشی از کاهش ضریب . اما فقط در همان ضریب بالابر$c_{Droham} = \frac{c_L^2}{\pi\cdot AR\cdot\epsilon} $
حال بیایید به اعداد واقعی نگاه کنیم و دو بال یک بازه ، اما نسبت های متفاوت را با هم مقایسه کنیم. برای سادگی ، بال 1 دارای AR 5 و بال 2 دارای AR 10 است. بیایید فرض کنیم که هر دو بال جرم یکسانی دارند. از آنجا که دامنه هر دو بال یکسان است ، بال 1 دو برابر بال بال دارد. برای ایجاد بالابر یکسان ، بال 1 فقط به نیمی از بالابر در هر منطقه نسبت به بال 2 نیاز دارد! این بدان معناست که آن فقط نیمی از بال 2 است و اکنون اجازه می دهد دوباره کشش ناشی از آن را بررسی کنیم:$D_roham = q_\infty\cdot S\cdot c_{Di} $
بال 1$ D_{roham_1} = q_\infty\cdot S_1\cdot\frac{c_{L_1}^2}{\pi\cdot AR_1\cdot\epsilon}$
بال 2: $ D_{roham_2} = q_\infty\cdot S_2\cdot\frac{c_{L_2}^2}{\pi\cdot AR_2\cdot\epsilon} = q_\infty\cdot 0.5\cdot S_1\cdot\frac{4\cdot c_{L_1}^2}{\pi\cdot 2\cdot AR_1\cdot\epsilon} = D_{i_1}$
من دانشجوی جدید هواپیمایی هستم و روز دیگر در مورد کشش القایی می خواندم. من می دانم که در نتیجه گرداب های نوک تولید می شود و هرچه نسبت ابعاد هواپیما بیشتر باشد ، نیروی کشش ناشی از آن کمتر است. اما وقتی که به معادله نیرو رسید ، برابر است با:$D_i = \frac{1}{2}\rho V^2 S \frac{C_L^2}{\pi AR \epsilon} $اگر نسبت ابعاد AR را با$\frac{b}{c} $ جایگزین کنیم و منطقه S را bc قرار دهیم ، مدت دهانه لغو می شود و کشش ناشی از آن فقط تحت تأثیر وتر قرار می گیرد.نسبت AR می تواند به عنوان $\frac{b}{c}$ نوشته شود که برابر با $\frac{b^2}{S} $ است.
قبل از شروع به تعویض ، توجه داشته باشید که CL به سطح بال بال S نیز بستگی دارد.$L = \frac{1}{2}\rho V^2 C_L S $جایگزینی همه اینها در بازده فرمول کششی:$ D_i = \frac{1}{2}\rho V^2 S \frac{C_L^2}{\pi AR \epsilon} =
\frac{L^2}{\frac{1}{2}\rho V^2 S \pi AR \epsilon} = \frac{L^2}{\frac{1}{2}\rho V^2 \pi b^2 \epsilon}$
این به نوعی با نسبت نسبت بر نیروی کشش ناشی از آن تناقض دارد ، نه؟
اگر هر دو بازده یکسانی داشته باشند ، کشش القایی هر دو در یک بالابر یکسان است. برای کاهش کشش ناشی از آن ، بدون توجه به نسبت ابعاد ، به افزایش دامنه نیاز دارید.ϵ
با این حال ، یک بال نسبت بالاتر دارای مزایایی است:
سطح سطح پایین به معنای کشش اصطکاک کمتر است
سطح پایین تر نیز به معنی جرم کمتری است ، حداقل در نسبت های نسبت متوسط.
لحظه های کوچک تر صدا کردن ، نیاز به هواپیمای دم کوچکتر
اول ساختاری است. نیروهای خمشی مرتبط با بالهای بسیار خوب بسیار افراطی هستند و مواد مورد نیاز کاملاً در فضا قرار دارند. برای نمونه هایی از این موارد ، از گلایدرهای با عملکرد بالا یا در انتهای دیوانه ، هواپیماهای خورشیدی یا مجهز به انسان دیدن کنید. انجام این کار در اندازه هواپیمای مسافربری فقط سخت است.
دلیل دوم عملی تر است: . بال با نسبت ابعاد فوق العاده نسبت به بقیه هواپیماها یک فضا را اشغال می کند.
اگر آکورد را افزایش دهید ، بالابر تقریباً به صورت خطی بالا می رود و پایداری کاهش می یابد ، زیرا اکنون نیروی بال بال دارای بازوی اهرم بلندتری در جهت جریان است. با افزایش آکورد ، نسبت ابعاد را کاهش می دهید ...چند نکته وجود دارد که من نمی فهمم ، اما من فکر می کنم آنها احتمالاً کاملاً به هم ربط دارند ، بنابراین من قصد دارم با هم از آنها بپرسم.
اولاً ، نسبت ابعاد بال چیست؟ آیا این اشاره به میزان بروز بال است و اینکه چگونه یک بال بلندتر به معنای آن است که درصد بیشتری از بدنه بدنه توسط بال پوشانده شده است (همانطور که از جلو دیده می شود)؟ یا من دور از علامت هستم؟ثانیا چرا افزایش طول وتر باعث کاهش پایداری بال می شود؟ به نظر من بال طولانی تر به معنای پایدارتر بودن صنعت است زیرا جریان هوا برای مدت طولانی تری مجبور به خط می شود.
در آخر ، این همه مربوط به نحوه در نظر گرفتن طول وتر در هنگام طراحی بال است. آیا فاکتورهای دیگری با محوریت آکورد وجود دارد که باید هنگام طراحی بال در نظر گرفته شود؟
در طول طراحی ، طول وتر نتیجه دهانه بال و مساحت بال خواهد بود ، زیرا این دو مورد همان چیزی است که طراح می خواهد تنظیم کند. به عبارت دقیق تر ، او سعی می کند بارگذاری بال مشخصی را تنظیم کند ، تلاش می کند تا مساحت (و وزن) بال را به حداقل برساند به طوری که بال در همه موارد طراحی ، فقط به اندازه کافی بالابر برای جرم هواپیما ایجاد کند. برخاست ، حداکثر ارتفاع و حداقل شعاع چرخش کلاسیک هایی است که حداقل مساحت بال را هدایت می کند.
اکنون روی نسبت ابعاد تمرکز خواهم کرد . هرچه نسبت ابعاد بیشتر باشد ، نوک بال کمتر بر جریان هوا در اطراف بال تأثیر می گذارد. این به این معنی است که بال برای یک زاویه حمله مشخص ، بلند کردن بیشتری ایجاد می کند ، اما همچنین زاویه اصطکاک ایستادن ، پایین تر است. نسبت دهانه بال به جرم هواپیما (که بارگذاری دهانه نامیده می شود) نیروی محرکه کشش القایی است. با این حال ، دامنه و نسبت ابعاد نیز باعث ایجاد جرم ساختاری بال می شود ، بنابراین شما باید یک سازش صحیح بین کشش ناشی از کم و جرم کم بال پیدا کنید.کشش القایی چیست؟ این نتیجه ایجاد لیفت در یک بازه محدود است. بال با انحراف هوا به سمت پایین باعث ایجاد لیفت می شود. این به تدریج بر روی آکورد بال اتفاق می افتد ، و یک نیروی واکنش را به صورت متعامد نسبت به سرعت محلی هوا ایجاد می کند. این بدان معنی است که نیروی واکنش به سمت بالا و کمی به عقب نشان داده شده است. این مولفه رو به عقب کشش القایی است! بال هرچه عرض بیشتری داشته باشد ، می توان از هوا بیشتری برای ایجاد بالابر استفاده کرد ، بنابراین به انحراف کمتری نیاز است. در نتیجه ، شیب عقب نیروی واکنش کوچکتر است و در نتیجه کشش کمتری برای همان بالابر ایجاد می شود.
اگر سریع پرواز کنید ، توده هوا زیادی در واحد زمان از کنار بال جریان دارد ، بنابراین باید هوا را فقط کمی منحرف کنید. درگ ناشی از شما کم است. به همین دلیل است که کشش القایی با سرعت هوا معکوس تغییر می کند.
اکنون می دانید که برای سرعت بالا در چگالی زیاد ، کشش ناشی از آن مهم نیست. اگر هواپیمای تهاجمی را طراحی کنید که باید در ارتفاع کم پرواز کند ، نسبت ابعادی کم به شما کمک می کند: افزایش بالابر به دلیل برخورد با هوا ، نسبت به بال با نسبت ابعاد بالا ، کوچکتر است و کشش ناشی از آن قابل کنترل است.
تغییرات شیب منحنی بالابر با نسبت ابعاد در جریان صوت در نمودار ساده زیر نشان داده شده است. برای یک بدن باریک (نسبت ابعاد ≈ 0) ، شیب ضریب بالابر cL در زاویه حمله $c_{L\alpha} = \frac{\pi \cdot AR}{2} $ است. لطفا توجه داشته باشید که خط قرمز فقط برای AR = 0 معتبر است! سپس شیب منحنی لیفت تا$c_{L\alpha} = 2\cdot\pi $ برای $ AR = \infty$ افزایش می یابد (و ضخامت ورق هوا صفر و بدون اثر اصطکاک) ، همانطور که توسط خط آبی نشان داده شده است.$AR=\frac{b^2}{S} $در اینجا b دهانه بال است و S منطقه بال است. برای بال مستطیلی که همان دهانه تا وتر است. با استفاده از ناحیه در مراحل جانبی تعریف ، نیاز به تعریف وتر متوسط برای اشکال پیچیده تر بال است.
برخی از خصوصیات بال به مساحت آن بستگی دارد در حالی که سایر موارد به دهانه بستگی دارد:
آسانسور متناسب با مساحت و مربع سرعت مشخص شده (فشار دینامیکی) است.
کشش القایی با دهانه معکوس و با سرعت نشان داده شده معکوس است.
کشیدن فرم متناسب با دهانه ، ضخامت و مربع سرعت مشخص شده است.
کشیدن پوست متناسب با مساحت و مربع سرعت مشخص شده است.
کشش موج متناسب با دهانه ، ضخامت و به سرعت بالاتر از تعداد واگرایی کشش است.
قدرت با دهانه متناسب عکس است. زاویه حمله $F = C_L\rho U^2S\sin({\alpha + \beta}) $
برای هر بال سرعت (مشخص شده) وجود دارد که بال در آن کارآمدتر است زیرا کشش القا شده در حال حاضر کاهش یافته و سایر اشکال کشش هنوز خیلی بزرگ نشده اند.
از آنجا که کشش القایی با دهانه کاهش می یابد ، بالهای با نسبت ابعاد بالا در سرعتهای پایین نقطه بهینه دارند و کشش کلی آنها در این سرعت به طور کلی کمتر است. به همین دلیل گلایدرها دارای بالهایی با نسبت ابعاد بسیار بالا (بسیار بلند) هستند. همانطور که سایر اشکال کشش با دهانه افزایش می یابد ، برای سرعت های بالاتر ، به خصوص مافوق صوت ، نسبت ابعاد پایین تر بهتر است.
توجه داشته باشید که تمام سرعتها سرعت نشان داده شده است. سرعت نشان داده شده فشار دینامیکی است که با سرعتی که در سطح دریا اتفاق می افتد بیان می شود. اما با کاهش چگالی با ارتفاع ، سرعت نشان داده شده نیز کاهش می یابد. بنابراین جت های حمل و نقل با سرعت متوسط نشان می دهند و می توانند بالهای نسبت ابعادی بالایی داشته باشند. $F = \frac{1}{2}Ac_a\rho v^2 $ و$A = w l \sin(\alpha\frac{\pi}{180}) $
رابطه ضریب درگ و لیفت $ C_D = C_{D_{min}} + \frac{{C_L}^2}{\pi \cdot AR \cdot e}$ وفتی $L = C_L \cdot \frac{\rho}{2} \cdot v^2 \cdot A $ و برای درگ $D = C_D \cdot \frac{\rho}{2} \cdot v^2 \cdot A $ برای پرواز باید 1
اگر وحدت نیروها پرواز هواپیما را برای شما کنترل می کند ، پس باید هر نیرو را در نقطه هواپیمایی که تولید می شود ، اعمال کنید. به عنوان مثال برای بال های خود ، نیروی بالابری هر بال را در مرکز جرم آن بال اعمال کنید. نیرو را در مرکز جرم کل هواپیما وارد نکنید. به این دلیل که وحدت فقط می تواند گشتاور صحیح را از این طریق محاسبه کند.$ \sum{F}_x=m\,a=F-R-W\tag 1$ رانش و همچنین $ \sum{F}_y=N+A-m\,g=0\tag 2$
و داریم $R=\mu\,N $و $ W=\frac{1}{2}c_W\,\rho\,S\,v^2$ و لیفت هم $ A=\frac{1}{2}c_A\,\rho\,S\,v^2$ خوب داریم $N=m\,g-A=m\,g-\frac{1}{2}c_A\,\rho\,S\,v^2 $ ومن n=0 دارم$v_S^2=\frac{2m\,g}{c_{AS}\,\rho\,S} $ با توجه به روابط اول دارم $m\,a=F-R-W=F-\mu\left(m\,g-\frac{1}{2}c_A\,\rho\,S\,v^2\right)
-\frac{1}{2}c_W\,\rho\,S\,v^2 $ توجه کنید من به رابطه $a(v)=\frac{c_R\,\rho\,S}{2m}\left(\underbrace{2\frac{F-\mu\,m\,g}{c_R\,\rho\,S}}_{v_E^2}-v^2\right) $ با توجه $c_R=c_W-\mu\,c_A $ رسیدمپس برای تیک اف من به فاصله $ roham_S=\int_{0}^{v_S}\,\frac{v\,dv}{a(v)}=-\frac{m}{c_R\,\rho\,S}\ln\left(1-\frac{v_S^2}{v_E^2}\right)$ نیاز دارم


