سلام به همه اعضا
چرا برای محاسبه فشار در یک ظرف بسته ارتفاع رو در نظر نمیگیریم و فشار رو در بالا و پایین و تمام نقاط ظرف یکسان فرض میکنیم. هر چند ظرف خیلی طویل باشه حتی چند صد کیلومتر !
ولی در فضای باز برای محاسبه فشار باید ارتفاع رو در نظر گرفت ؟ (این رو هم میدونم که فشار در بالاترین نقطه اتمسفر صفر است)
در منابع فارسی جواب مناسبی نیافتم و اگه عبارت زیر رو سرچ کنید در منابع انگلیسی هم جواب های متضادی داده شده. برخی گفتند که در یک ظرف سربسته فشار بالا و پایین متفاوت هست و برخی هم گفتند که همه جا یکسان است
Gas pressure at the top and bottom of the container
خوشحال میشم دوستان راهنمایی کنند ...
تاثیر ارتفاع در فشار گاز در یک ظرف سربسته طویل
- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3265-
سپاس: 5494
- جنسیت:
تماس:
Re: تاثیر ارتفاع در فشار گاز در یک ظرف سربسته طویل
برای یک ظرف مهر و موم شده و سفت و سخت، فشار گاز داخل تغییر نمی کند.
آیا گرانش فشار بالایی در ته ظرف پر از گاز ایجاد می کند؟یک مدل ساده وجود دارد که افکار شما را در بر می گیرد: ارتفاع ترازو. بگو تو در این گاز هستی. وقتی ارتفاع ترازو را طی می کنید، فشار یک ضریب e افزایش می یابد. این انگیزه می تواند به شرح زیر باشد:
ما رابطه نمایی ارتفاع و فشار را می خواهیم، به طوری که$P=P_0\exp(-\frac{z}{H}$ این نیز راه حل یک معادله دیفرانسیل به شکل $\frac{\mathrm{d}P}{\mathrm{d}z}=-\frac{P}{H}$ است. اما از سوی دیگر این نیز باید درست باشد که تغییر فشار با ارتفاع متناسب با چگالی ضربدر شتاب گرانشی است - چگالی بیشتر به معنای فشار بیشتر است، اما کشش گرانشی قویتر باید فشار بیشتری را نیز نشان دهد، بنابراین چیزی شبیه به $\frac{\mathrm{d}P}{\mathrm{d}z}=-g\rho$. با جمع کردن هر دو معادله به این نتیجه می رسیم:
$\begin{equation}
\frac{P}{H}=g\rho
\end{equation}$
از گاز ایده آل و ترمودینامیک می دانیم: PV=nRT و طبق تعریف ρ=MV داریم که منجر به
$\begin{align}
\frac{nRT}{VH}&=g\frac{M}{V}\\
\frac{nRT}{H}&=gM\\
\frac{nRT}{gM}&=H
\end{align}$
بنابراین فشار با $\exp(-\frac{z}{\frac{nRT}{gM}})=\exp(-\frac{zgM}{nRT})$افزایش می یابد.
بنابراین بله، همیشه در یک ظرف گاز اختلاف فشار وجود دارد و این اختلاف حتی به طور تصاعدی افزایش می یابد!
وقتی می گوییم فشار وارد شده توسط گاز، فشار وارد شده توسط گاز بر روی ظرف به دلیل برخورد ذرات با دیواره ظرف در هنگام نگهداری در ظرف دربسته، از PV=nRT برای تعریف آن استفاده می کنیم که در اینجا فشار ناشی از وزن هوا بسیار کم است، بنابراین نادیده گرفته شده است (مثلاً تغییر فشار در موج صوتی است) اما فشار اتمسفر به دلیل وزن گاز است زیرا فشار ناشی از برخورد ذرات با زمین به دلیل مقدار بسیار کم می تواند نادیده گرفته شود.برای شروع، به سیستمی که در حال تجزیه و تحلیل هستید بستگی دارد. گازهای اتمسفر اساساً یک سیستم باز هستند که به دلیل نیروی گرانش در کنار هم می مانند. تمام گازهای پایین تر وزن گازهای فوق را تحمل می کنند. نیروی این وزنه بر روی تمام هوا بر اساس مقدار جرم بالای آن فشار می آورد.
در یک ظرف دربسته، ما اغلب وزن گاز را در نظر نمی گیریم زیرا اگر ارتفاع ظرف خیلی زیاد نباشد، اثرات وزن حداقل است. در یک ظرف بسیار بلند، فشار نیز تحت تأثیر وزن قرار می گیرد. گاز موجود در قسمت پایین به طور قابل توجهی فشار بیشتری نسبت به گاز بالا خواهد داشت، زیرا گاز موجود در قسمت پایین باید تمام وزن گاز بالای خود را تحمل کند.
وجود ظرف مهم نیست، مهم بلندی ظرف است. اگر به اندازه کافی بلند باشد، وزن گاز تاثیر محسوسی بر توزیع فشار خواهد داشت. از نظر فنی، هر ظرف بسته در گرانش دارای این خواهد بود. اما مگر اینکه ظرف بسیار بلند باشد، تفاوت بسیار ناچیز است
چرا (فرض می کنیم) گاز در همه جا در یک ظرف بسته فشار یکسانی را اعمال می کند
عدم تعادل فشار خود باعث ایجاد جریان داخلی در گاز می شود. بنابراین اگر گاز به حالت تعادل رسیده باشد فشار باید در همه جا یکسان باشد.
موارد فوق برای یک گاز در شرایط عادی، بدون هیچ میدان اعمالی مانند میدان گرانشی است. اگر چنین میدانی وجود داشته باشد، گاز جریان می یابد تا زمانی که گرادیان فشار نیرویی را ایجاد کند که فقط اثرات میدان را متعادل می کند.
برای محاسبه کامل این اثرات می توان از مفهوم پتانسیل شیمیایی و قانون دوم ترمودینامیک استفاده کرد.
این واقعیت وجود دارد که کمیت های ترمودینامیکی مانند فشار نیز دچار نوسان می شوند. نظرات بالا در مورد یکنواختی برای فشار میانگین زمانی در هر نقطه اعمال می شود.
تعمیم به مایعات
استدلال های بالا به طور کلی در مورد سیالات اعمال می شود، نه فقط برای گازها (و بنابراین محدود به گاز ایده آل نیست). تا زمانی که سیال بتواند جریان داشته باشد، هر شیب فشاری باعث ایجاد جریان می شود، بنابراین وقتی سیال در یک ظرف بسته به تعادل می رسد، فشار باید یکنواخت باشد.
این بستگی به وضوح دستگاه اندازه گیری شما دارد.
یک گاز حاوی حدود $10^{22}$ مولکول است که در اطراف زیپ شده اند. فشار روی دیواره ظرف به دلیل نیروی کوچکی است که این مولکول ها هنگام برخورد با دیواره وارد می کنند. اگر بتوانید در یک لحظه از هر یک از دیوارها عکس بگیرید، تعداد معینی مولکول با هر دیوار برخورد می کند. با این حال، این عدد از دیوار به دیوار متفاوت خواهد بود. اگر می توانستید فشارهای کوچک را اندازه بگیرید، تفاوت وجود داشت. نمیدانم دستگاههایی داریم که بتوانیم فشارها را با این حساسیت اندازهگیری کنیم یا خیر.
در مقیاس کلان، تفاوت از دیوار به دیوار نامحسوس است. کافی است بگوییم فشار در هر نقطه از دیواره ظرف ثابت است.
ناحیه ای از سیال را در نظر بگیرید و اجازه دهید S سطح آن ناحیه باشد. اگر$\int_Sp\vec n$را در نظر بگیرید، جایی که$\vec n$ بردار نرمال است، این نیروی خالصی است که فشار سیال بیرونی بر جرم سیال داخل ناحیه وارد میکند. اگر این نیرو را تنها نیروی وارد بر سیال در نظر بگیریم، برای اینکه سیال داخل منطقه شتاب نداشته باشد، این نیرو باید صفر باشد. برای اینکه این برای هر منطقه صفر باشد، فشار باید در همه جا برابر باشد.
برای سیالات در یک میدان گرانشی، نیروی وارد بر سیال، نیروی فشار به اضافه وزن آن است، بنابراین نیروی فشار باید از نظر بزرگی برابر و در جهت مخالف وزن آن باشد. این نیروی فشار را «شناوری» میگویند و باید یک گرادیان در فشار وجود داشته باشد تا باعث شود شناوری برابر با وزن باشد. با این حال، برای تفاوت های کوچک در ارتفاع، این تغییر در فشار کوچک است، و می تواند برای بسیاری از اهداف نادیده گرفته شود.
میانگین انرژی جنبشی یک مولکول گاز (دما) در همه جای ظرف یکسان است، زیرا وقتی مولکول هایی با انرژی های مختلف با هم برخورد می کنند، از نظر آماری احتمال دارد که انرژی را به طور مساوی پس از برخورد توزیع کنند. دما یکنواخت می شود. بنابراین سرعت متوسط مولکول ها نیز در همه جا یکسان است.
سرعت متوسط مولکول های گاز در همه جا صفر است، با فرض اینکه جریانی وجود نداشته باشد. (در واقعیت، اگرچه جریان ها واقعاً می توانند بر فشار نسبی در نقاط مختلف تأثیر بگذارند، برای ایجاد تفاوت به جریان های واقعاً قوی نیاز دارید. جریان های ناشی از همرفت بسیار کوچک هستند).
چگالی متوسط مولکول ها در همه جا یکسان است. اگر هر صفحه تقسیم کننده ای را تصور کنید، سپس با داده های (1) و (2)، اگر مولکول های بیشتری در یک طرف وجود داشته باشد، جریان خالص به سمت دیگر وجود خواهد داشت.
فشار متوسط در هر نقطه از سطح ظرف متناسب با سرعت و چگالی مولکول های گاز در آنجا است، زیرا این میزان کل انتقال تکانه به دیواره ظرف است که متناسب با سرعت مولکول ضربدر سرعت برخورد و برخورد است. نرخ متناسب با سرعت و چگالی است، که قبلاً تعیین کردهایم در همه جا یکسان هستند.
این فرض برای ظرفی که به اندازه کافی در امتداد جهت بردار گرانش محلی برای تفاوت های ناشی از نیروی گرانشی روی مولکول ها به ماده بزرگ است، درست نیست.
مثلاً اگر ظرفی با ارتفاع حدود 5000 متر (!!!) و با دیوارهای سفت و سخت بسازید، فشار در قسمت بالا تقریباً نصف اتمسفر (حدود 50 کیلو پاسکال) کمتر از فشار پایین خواهد بود. بیشتر ظروف "بلندتر از این" هستند و معمولاً می توان از تفاوت ها چشم پوشی کرد.
رفتار دو گاز در یک ظرف بستهمرتب شده بر اساس:
در هر دمایی T قضیه همتقسیم به ما میگوید که یک مولکول در یک گاز ایدهآل دارای انرژی جنبشی $\tfrac{3}{2}kT$خواهد بود. از آنجایی که انرژی جنبشی با سرعت $E = \tfrac{1}{2}mv^2$ مرتبط است، میتوانیم از آن برای تخمین سرعت مولکولهای گاز در دمای اتاق استفاده کنیم و برای آرگون و نیتروژن حدود 400 تا 500 متر بر ثانیه است.
بنابراین مولکولهای گاز در ظرف شما همه با سرعت صدها متر در ثانیه به اطراف میچرخند، و جای تعجب نیست که این بدان معناست که آنها با یکدیگر مخلوط میشوند. سرعت ها آنقدر زیاد است که وزن های مختلف دو نوع مولکول اساساً تأثیری در جداسازی آنها ندارد.
گرانش تاثیری دارد و این با معادله بارومتری توصیف می شود:
$\frac{\rho}{\rho_0} = \exp\left( \frac{-gM(h - h_0)}{RT} \right)$
این چگالی ρ را به ارتفاع h مرتبط می کند. g شتاب گرانشی و M جرم مولی گاز است. بیایید ظرف یک لیتری شما را برداریم، در این صورت ارتفاع ظرف حدود 10 سانتی متر و جرم مولی نیتروژن 0.028 کیلوگرم است. اگر این مقادیر را به معادله فشار سنجی وارد کنیم، نسبت چگالی بین بالا و پایین ظرف در دمای اتاق برابر است:
$\frac{\rho}{\rho_0} \approx 0.999989$
این برای نیتروژن است. جرم مولی آرگون در 0.04 کیلوگرم بزرگتر است، اما این فقط نسبت ρ/ρ0 را به 0.999984 کاهش می دهد. بنابراین، اگرچه در اصل نسبت آرگون به نیتروژن کمی از پایین به بالای ظرف تغییر می کند، این تغییر به طور ناپدید کننده ای کوچک است. در عمل ترکیب گاز یکنواخت باقی می ماند.
اگر ظرف خود را بسیار بزرگ کنید، به عنوان مثال. در مورد ضخامت اتمسفر زمین، تغییر در ترکیب به طور قابل اندازه گیری بزرگ می شود، به همین دلیل است که ترکیب جو زمین با ارتفاع تغییر می کند.
بخش دوم سوال شما کمی متفاوت است زیرا با گازهای جدا شده شروع می شود و می پرسد که چقدر سریع مخلوط می شوند. با توجه به سرعت حرکت مولکول های گاز، ممکن است فکر کنید اختلاط بسیار سریع است، اما در واقع اینطور نیست. مشکل این است که مولکول های گاز با یکدیگر برخورد می کنند و در جهت های تصادفی به عقب برمی گردند. میانگین مسافتی که یک مولکول گاز قبل از برخورد با مولکول دیگر طی می کند، مسیر آزاد متوسط نامیده می شود و در دما و فشار اتاق میانگین مسیر آزاد حدود 0.1 میکرون است.
بنابراین حتی اگر یک مولکول نیتروژن با سرعتی در حدود 500 متر بر ثانیه حرکت می کند، به طور تصادفی و نه در یک خط مستقیم حرکت می کند. اگر با دو گاز جدا شده در لایه های مختلف شروع کنید، مخلوط کردن به طرز شگفت آوری کند است. در واقع همانطور که در سوال مطرح شد چرا مخلوط کردن گازهای هلیوم و نیتروژن دشوار است؟ ممکن است آنقدر کند باشد که روزها یا هفته ها طول بکشد تا اتفاق بیفتد.
با فرض اینکه مخلوط را به هیچ وجه هم نمی زنید، اختلاط با انتشار انجام می شود و با معادله انتشار توصیف می شود.
برای سیالات، فشار به طور کلی به صورت نوشته می شود
P=ρgh
که ρ چگالی سیال، g ثابت شتاب گرانشی و h عمق است. فشار با افزایش عمق افزایش مییابد زیرا وزن تمام سیال در بالا به سمت پایین فشار میآورد و هرچه پایینتر بروید، سیال بیشتری در بالا قرار میگیرد.
حال باید در نظر بگیریم که خود گازها نیز سیال هستند، پس همین موضوع در مورد گازها نیز صادق است. با این حال، در مورد گاز، مقدار چگالی بسیار پایین است، بنابراین برای هر ظرف ذخیره سازی با اندازه معقول برای گاز، فشار ناشی از گرانش بسیار کم خواهد بود. با این حال، برای مقادیر زیادی از گاز، به عنوان مثال جو زمین، این مورد در حال حاضر مطرح است، زیرا ارتفاع جو بسیار زیاد است. ما این تفاوت را به عنوان فشار هوا احساس می کنیم و در ارتفاعات بالاتر (عمق کمتر)، دقیقاً به دلیل این تأثیر، فشار زیادی را احساس نمی کنیم.
فشار گازها نیز بر خلاف مایع می تواند تحت تأثیر دمای گاز باشد. در یک مایع، فعل و انفعالات شل بین ذرات آنها را در کنار هم نگه می دارد که اجازه نمی دهد ذرات آزادانه از یکدیگر دور شوند مانند یک گاز. اما در یک گاز، ذرات می توانند آزادانه حرکت کنند. برای یک گاز ایده آل، رابطه ای برای فشار دارید که به شکل زیر است:
$P = \frac{Nk_BT}{V}$
که در آن N تعداد ذرات، kB یک ثابت، T دما و V حجم ظرف است. در این حالت شما به تمام دیواره های یک ظرف فشار ثابتی دارید. این اثر غالب برای گازهایی است که در هر ظرفی با اندازه معقول ذخیره می شوند، و اینجاست که تفاوت بین گازها و مایعات به وجود می آید.
برای اینکه فشار یک مایع روی تمام دیواره های ظروف یکسان باشد، باید اثرات گرانش را از بین ببرید.
چرا وقتی گاز درون یک ظرف بسته با اتمسفر تماس ندارد، فشار اتمسفر را تجربه می کند؟اما در واقع یک گاز درون یک ظرف بسته لزوماً فشار اتمسفر را تجربه نمی کند. اگر تا به حال یک بطری پاپ را تکان داده باشید و سپس آن را باز کرده باشید، متوجه خواهید شد که فشار گاز داخل آن بسیار بیشتر از فشار اتمسفر است. این مثالی است که در آن فشار داخل ظرف بسته بیشتر از فشار اتمسفر است، اما می تواند کمتر نیز باشد.
اتفاقی که برای گاز یک ظرف می افتد بستگی به انعطاف پذیری ظرف دارد. اگر یک بطری شیشه ای بردارم و نیمی از هوا را بیرون بکشم، گاز داخل آن در نیمی از فشار اتمسفر باقی می ماند. این به این دلیل است که دیواره های شیشه ای بطری سفت هستند و مقداری از فشار را تحمل می کنند.
از طرف دیگر اگر یک کیسه پلاستیکی را با گاز پر کنم و مقداری از آن را بیرون بکشم، فشار داخل کیسه در فشار اتمسفر باقی می ماند. به این دلیل که کیسه پلاستیکی انعطاف پذیر است. جو روی کیسه فشار می آورد و کیسه فشار را به گاز داخل آن منتقل می کند.
تصور کنید گاز در داخل یک پیستون آب بندی شده است، مانند این: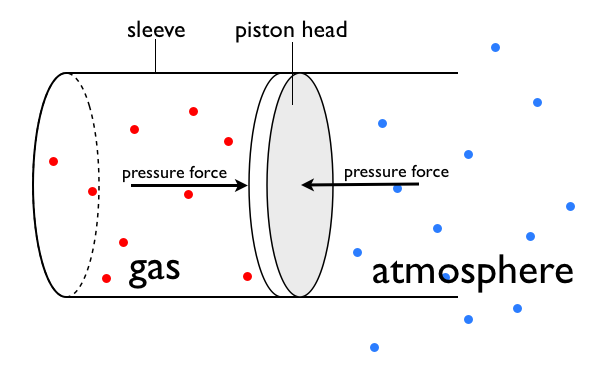
گاز در پیستون
سر پیستون برای حرکت در آستین آزاد است که باعث تغییر حجم گاز می شود. ما از تجربه می دانیم که سر پیستون به سرعت موقعیت تعادلی پیدا می کند که در آن دیگر حرکت نمی کند. اگر پیستون از حرکت باز ایستاد، به این معنی است که شتاب نمیگیرد و اگر شتاب نمیگیرد، به این معنی است که مجموع نیروهای وارد بر آن باید صفر شود.
هم گاز داخل پیستون و هم اتمسفر خارج از آن بر پیستون نیرو وارد می کنند. بزرگی این نیروها برابر است با فشار گاز (یا اتمسفر)، برابر مساحتی که بر آن تأثیر می گذارد. دو نیرو در جهت مخالف عمل می کنند و پیستون در هر طرف دارای مساحت یکسانی است، به این معنی که دو فشار باید برابر باشند. به همین دلیل است که گازهای داخل ظروف به همان فشار هوای بیرون می رسند - حجم گاز تا زمانی که نیروهای وارد بر ظرف متعادل شوند تنظیم می شود.
آیا گرانش فشار بالایی در ته ظرف پر از گاز ایجاد می کند؟یک مدل ساده وجود دارد که افکار شما را در بر می گیرد: ارتفاع ترازو. بگو تو در این گاز هستی. وقتی ارتفاع ترازو را طی می کنید، فشار یک ضریب e افزایش می یابد. این انگیزه می تواند به شرح زیر باشد:
ما رابطه نمایی ارتفاع و فشار را می خواهیم، به طوری که$P=P_0\exp(-\frac{z}{H}$ این نیز راه حل یک معادله دیفرانسیل به شکل $\frac{\mathrm{d}P}{\mathrm{d}z}=-\frac{P}{H}$ است. اما از سوی دیگر این نیز باید درست باشد که تغییر فشار با ارتفاع متناسب با چگالی ضربدر شتاب گرانشی است - چگالی بیشتر به معنای فشار بیشتر است، اما کشش گرانشی قویتر باید فشار بیشتری را نیز نشان دهد، بنابراین چیزی شبیه به $\frac{\mathrm{d}P}{\mathrm{d}z}=-g\rho$. با جمع کردن هر دو معادله به این نتیجه می رسیم:
$\begin{equation}
\frac{P}{H}=g\rho
\end{equation}$
از گاز ایده آل و ترمودینامیک می دانیم: PV=nRT و طبق تعریف ρ=MV داریم که منجر به
$\begin{align}
\frac{nRT}{VH}&=g\frac{M}{V}\\
\frac{nRT}{H}&=gM\\
\frac{nRT}{gM}&=H
\end{align}$
بنابراین فشار با $\exp(-\frac{z}{\frac{nRT}{gM}})=\exp(-\frac{zgM}{nRT})$افزایش می یابد.
بنابراین بله، همیشه در یک ظرف گاز اختلاف فشار وجود دارد و این اختلاف حتی به طور تصاعدی افزایش می یابد!
وقتی می گوییم فشار وارد شده توسط گاز، فشار وارد شده توسط گاز بر روی ظرف به دلیل برخورد ذرات با دیواره ظرف در هنگام نگهداری در ظرف دربسته، از PV=nRT برای تعریف آن استفاده می کنیم که در اینجا فشار ناشی از وزن هوا بسیار کم است، بنابراین نادیده گرفته شده است (مثلاً تغییر فشار در موج صوتی است) اما فشار اتمسفر به دلیل وزن گاز است زیرا فشار ناشی از برخورد ذرات با زمین به دلیل مقدار بسیار کم می تواند نادیده گرفته شود.برای شروع، به سیستمی که در حال تجزیه و تحلیل هستید بستگی دارد. گازهای اتمسفر اساساً یک سیستم باز هستند که به دلیل نیروی گرانش در کنار هم می مانند. تمام گازهای پایین تر وزن گازهای فوق را تحمل می کنند. نیروی این وزنه بر روی تمام هوا بر اساس مقدار جرم بالای آن فشار می آورد.
در یک ظرف دربسته، ما اغلب وزن گاز را در نظر نمی گیریم زیرا اگر ارتفاع ظرف خیلی زیاد نباشد، اثرات وزن حداقل است. در یک ظرف بسیار بلند، فشار نیز تحت تأثیر وزن قرار می گیرد. گاز موجود در قسمت پایین به طور قابل توجهی فشار بیشتری نسبت به گاز بالا خواهد داشت، زیرا گاز موجود در قسمت پایین باید تمام وزن گاز بالای خود را تحمل کند.
وجود ظرف مهم نیست، مهم بلندی ظرف است. اگر به اندازه کافی بلند باشد، وزن گاز تاثیر محسوسی بر توزیع فشار خواهد داشت. از نظر فنی، هر ظرف بسته در گرانش دارای این خواهد بود. اما مگر اینکه ظرف بسیار بلند باشد، تفاوت بسیار ناچیز است
چرا (فرض می کنیم) گاز در همه جا در یک ظرف بسته فشار یکسانی را اعمال می کند
عدم تعادل فشار خود باعث ایجاد جریان داخلی در گاز می شود. بنابراین اگر گاز به حالت تعادل رسیده باشد فشار باید در همه جا یکسان باشد.
موارد فوق برای یک گاز در شرایط عادی، بدون هیچ میدان اعمالی مانند میدان گرانشی است. اگر چنین میدانی وجود داشته باشد، گاز جریان می یابد تا زمانی که گرادیان فشار نیرویی را ایجاد کند که فقط اثرات میدان را متعادل می کند.
برای محاسبه کامل این اثرات می توان از مفهوم پتانسیل شیمیایی و قانون دوم ترمودینامیک استفاده کرد.
این واقعیت وجود دارد که کمیت های ترمودینامیکی مانند فشار نیز دچار نوسان می شوند. نظرات بالا در مورد یکنواختی برای فشار میانگین زمانی در هر نقطه اعمال می شود.
تعمیم به مایعات
استدلال های بالا به طور کلی در مورد سیالات اعمال می شود، نه فقط برای گازها (و بنابراین محدود به گاز ایده آل نیست). تا زمانی که سیال بتواند جریان داشته باشد، هر شیب فشاری باعث ایجاد جریان می شود، بنابراین وقتی سیال در یک ظرف بسته به تعادل می رسد، فشار باید یکنواخت باشد.
این بستگی به وضوح دستگاه اندازه گیری شما دارد.
یک گاز حاوی حدود $10^{22}$ مولکول است که در اطراف زیپ شده اند. فشار روی دیواره ظرف به دلیل نیروی کوچکی است که این مولکول ها هنگام برخورد با دیواره وارد می کنند. اگر بتوانید در یک لحظه از هر یک از دیوارها عکس بگیرید، تعداد معینی مولکول با هر دیوار برخورد می کند. با این حال، این عدد از دیوار به دیوار متفاوت خواهد بود. اگر می توانستید فشارهای کوچک را اندازه بگیرید، تفاوت وجود داشت. نمیدانم دستگاههایی داریم که بتوانیم فشارها را با این حساسیت اندازهگیری کنیم یا خیر.
در مقیاس کلان، تفاوت از دیوار به دیوار نامحسوس است. کافی است بگوییم فشار در هر نقطه از دیواره ظرف ثابت است.
ناحیه ای از سیال را در نظر بگیرید و اجازه دهید S سطح آن ناحیه باشد. اگر$\int_Sp\vec n$را در نظر بگیرید، جایی که$\vec n$ بردار نرمال است، این نیروی خالصی است که فشار سیال بیرونی بر جرم سیال داخل ناحیه وارد میکند. اگر این نیرو را تنها نیروی وارد بر سیال در نظر بگیریم، برای اینکه سیال داخل منطقه شتاب نداشته باشد، این نیرو باید صفر باشد. برای اینکه این برای هر منطقه صفر باشد، فشار باید در همه جا برابر باشد.
برای سیالات در یک میدان گرانشی، نیروی وارد بر سیال، نیروی فشار به اضافه وزن آن است، بنابراین نیروی فشار باید از نظر بزرگی برابر و در جهت مخالف وزن آن باشد. این نیروی فشار را «شناوری» میگویند و باید یک گرادیان در فشار وجود داشته باشد تا باعث شود شناوری برابر با وزن باشد. با این حال، برای تفاوت های کوچک در ارتفاع، این تغییر در فشار کوچک است، و می تواند برای بسیاری از اهداف نادیده گرفته شود.
میانگین انرژی جنبشی یک مولکول گاز (دما) در همه جای ظرف یکسان است، زیرا وقتی مولکول هایی با انرژی های مختلف با هم برخورد می کنند، از نظر آماری احتمال دارد که انرژی را به طور مساوی پس از برخورد توزیع کنند. دما یکنواخت می شود. بنابراین سرعت متوسط مولکول ها نیز در همه جا یکسان است.
سرعت متوسط مولکول های گاز در همه جا صفر است، با فرض اینکه جریانی وجود نداشته باشد. (در واقعیت، اگرچه جریان ها واقعاً می توانند بر فشار نسبی در نقاط مختلف تأثیر بگذارند، برای ایجاد تفاوت به جریان های واقعاً قوی نیاز دارید. جریان های ناشی از همرفت بسیار کوچک هستند).
چگالی متوسط مولکول ها در همه جا یکسان است. اگر هر صفحه تقسیم کننده ای را تصور کنید، سپس با داده های (1) و (2)، اگر مولکول های بیشتری در یک طرف وجود داشته باشد، جریان خالص به سمت دیگر وجود خواهد داشت.
فشار متوسط در هر نقطه از سطح ظرف متناسب با سرعت و چگالی مولکول های گاز در آنجا است، زیرا این میزان کل انتقال تکانه به دیواره ظرف است که متناسب با سرعت مولکول ضربدر سرعت برخورد و برخورد است. نرخ متناسب با سرعت و چگالی است، که قبلاً تعیین کردهایم در همه جا یکسان هستند.
این فرض برای ظرفی که به اندازه کافی در امتداد جهت بردار گرانش محلی برای تفاوت های ناشی از نیروی گرانشی روی مولکول ها به ماده بزرگ است، درست نیست.
مثلاً اگر ظرفی با ارتفاع حدود 5000 متر (!!!) و با دیوارهای سفت و سخت بسازید، فشار در قسمت بالا تقریباً نصف اتمسفر (حدود 50 کیلو پاسکال) کمتر از فشار پایین خواهد بود. بیشتر ظروف "بلندتر از این" هستند و معمولاً می توان از تفاوت ها چشم پوشی کرد.
رفتار دو گاز در یک ظرف بستهمرتب شده بر اساس:
در هر دمایی T قضیه همتقسیم به ما میگوید که یک مولکول در یک گاز ایدهآل دارای انرژی جنبشی $\tfrac{3}{2}kT$خواهد بود. از آنجایی که انرژی جنبشی با سرعت $E = \tfrac{1}{2}mv^2$ مرتبط است، میتوانیم از آن برای تخمین سرعت مولکولهای گاز در دمای اتاق استفاده کنیم و برای آرگون و نیتروژن حدود 400 تا 500 متر بر ثانیه است.
بنابراین مولکولهای گاز در ظرف شما همه با سرعت صدها متر در ثانیه به اطراف میچرخند، و جای تعجب نیست که این بدان معناست که آنها با یکدیگر مخلوط میشوند. سرعت ها آنقدر زیاد است که وزن های مختلف دو نوع مولکول اساساً تأثیری در جداسازی آنها ندارد.
گرانش تاثیری دارد و این با معادله بارومتری توصیف می شود:
$\frac{\rho}{\rho_0} = \exp\left( \frac{-gM(h - h_0)}{RT} \right)$
این چگالی ρ را به ارتفاع h مرتبط می کند. g شتاب گرانشی و M جرم مولی گاز است. بیایید ظرف یک لیتری شما را برداریم، در این صورت ارتفاع ظرف حدود 10 سانتی متر و جرم مولی نیتروژن 0.028 کیلوگرم است. اگر این مقادیر را به معادله فشار سنجی وارد کنیم، نسبت چگالی بین بالا و پایین ظرف در دمای اتاق برابر است:
$\frac{\rho}{\rho_0} \approx 0.999989$
این برای نیتروژن است. جرم مولی آرگون در 0.04 کیلوگرم بزرگتر است، اما این فقط نسبت ρ/ρ0 را به 0.999984 کاهش می دهد. بنابراین، اگرچه در اصل نسبت آرگون به نیتروژن کمی از پایین به بالای ظرف تغییر می کند، این تغییر به طور ناپدید کننده ای کوچک است. در عمل ترکیب گاز یکنواخت باقی می ماند.
اگر ظرف خود را بسیار بزرگ کنید، به عنوان مثال. در مورد ضخامت اتمسفر زمین، تغییر در ترکیب به طور قابل اندازه گیری بزرگ می شود، به همین دلیل است که ترکیب جو زمین با ارتفاع تغییر می کند.
بخش دوم سوال شما کمی متفاوت است زیرا با گازهای جدا شده شروع می شود و می پرسد که چقدر سریع مخلوط می شوند. با توجه به سرعت حرکت مولکول های گاز، ممکن است فکر کنید اختلاط بسیار سریع است، اما در واقع اینطور نیست. مشکل این است که مولکول های گاز با یکدیگر برخورد می کنند و در جهت های تصادفی به عقب برمی گردند. میانگین مسافتی که یک مولکول گاز قبل از برخورد با مولکول دیگر طی می کند، مسیر آزاد متوسط نامیده می شود و در دما و فشار اتاق میانگین مسیر آزاد حدود 0.1 میکرون است.
بنابراین حتی اگر یک مولکول نیتروژن با سرعتی در حدود 500 متر بر ثانیه حرکت می کند، به طور تصادفی و نه در یک خط مستقیم حرکت می کند. اگر با دو گاز جدا شده در لایه های مختلف شروع کنید، مخلوط کردن به طرز شگفت آوری کند است. در واقع همانطور که در سوال مطرح شد چرا مخلوط کردن گازهای هلیوم و نیتروژن دشوار است؟ ممکن است آنقدر کند باشد که روزها یا هفته ها طول بکشد تا اتفاق بیفتد.
با فرض اینکه مخلوط را به هیچ وجه هم نمی زنید، اختلاط با انتشار انجام می شود و با معادله انتشار توصیف می شود.
برای سیالات، فشار به طور کلی به صورت نوشته می شود
P=ρgh
که ρ چگالی سیال، g ثابت شتاب گرانشی و h عمق است. فشار با افزایش عمق افزایش مییابد زیرا وزن تمام سیال در بالا به سمت پایین فشار میآورد و هرچه پایینتر بروید، سیال بیشتری در بالا قرار میگیرد.
حال باید در نظر بگیریم که خود گازها نیز سیال هستند، پس همین موضوع در مورد گازها نیز صادق است. با این حال، در مورد گاز، مقدار چگالی بسیار پایین است، بنابراین برای هر ظرف ذخیره سازی با اندازه معقول برای گاز، فشار ناشی از گرانش بسیار کم خواهد بود. با این حال، برای مقادیر زیادی از گاز، به عنوان مثال جو زمین، این مورد در حال حاضر مطرح است، زیرا ارتفاع جو بسیار زیاد است. ما این تفاوت را به عنوان فشار هوا احساس می کنیم و در ارتفاعات بالاتر (عمق کمتر)، دقیقاً به دلیل این تأثیر، فشار زیادی را احساس نمی کنیم.
فشار گازها نیز بر خلاف مایع می تواند تحت تأثیر دمای گاز باشد. در یک مایع، فعل و انفعالات شل بین ذرات آنها را در کنار هم نگه می دارد که اجازه نمی دهد ذرات آزادانه از یکدیگر دور شوند مانند یک گاز. اما در یک گاز، ذرات می توانند آزادانه حرکت کنند. برای یک گاز ایده آل، رابطه ای برای فشار دارید که به شکل زیر است:
$P = \frac{Nk_BT}{V}$
که در آن N تعداد ذرات، kB یک ثابت، T دما و V حجم ظرف است. در این حالت شما به تمام دیواره های یک ظرف فشار ثابتی دارید. این اثر غالب برای گازهایی است که در هر ظرفی با اندازه معقول ذخیره می شوند، و اینجاست که تفاوت بین گازها و مایعات به وجود می آید.
برای اینکه فشار یک مایع روی تمام دیواره های ظروف یکسان باشد، باید اثرات گرانش را از بین ببرید.
چرا وقتی گاز درون یک ظرف بسته با اتمسفر تماس ندارد، فشار اتمسفر را تجربه می کند؟اما در واقع یک گاز درون یک ظرف بسته لزوماً فشار اتمسفر را تجربه نمی کند. اگر تا به حال یک بطری پاپ را تکان داده باشید و سپس آن را باز کرده باشید، متوجه خواهید شد که فشار گاز داخل آن بسیار بیشتر از فشار اتمسفر است. این مثالی است که در آن فشار داخل ظرف بسته بیشتر از فشار اتمسفر است، اما می تواند کمتر نیز باشد.
اتفاقی که برای گاز یک ظرف می افتد بستگی به انعطاف پذیری ظرف دارد. اگر یک بطری شیشه ای بردارم و نیمی از هوا را بیرون بکشم، گاز داخل آن در نیمی از فشار اتمسفر باقی می ماند. این به این دلیل است که دیواره های شیشه ای بطری سفت هستند و مقداری از فشار را تحمل می کنند.
از طرف دیگر اگر یک کیسه پلاستیکی را با گاز پر کنم و مقداری از آن را بیرون بکشم، فشار داخل کیسه در فشار اتمسفر باقی می ماند. به این دلیل که کیسه پلاستیکی انعطاف پذیر است. جو روی کیسه فشار می آورد و کیسه فشار را به گاز داخل آن منتقل می کند.
تصور کنید گاز در داخل یک پیستون آب بندی شده است، مانند این:

گاز در پیستون
سر پیستون برای حرکت در آستین آزاد است که باعث تغییر حجم گاز می شود. ما از تجربه می دانیم که سر پیستون به سرعت موقعیت تعادلی پیدا می کند که در آن دیگر حرکت نمی کند. اگر پیستون از حرکت باز ایستاد، به این معنی است که شتاب نمیگیرد و اگر شتاب نمیگیرد، به این معنی است که مجموع نیروهای وارد بر آن باید صفر شود.
هم گاز داخل پیستون و هم اتمسفر خارج از آن بر پیستون نیرو وارد می کنند. بزرگی این نیروها برابر است با فشار گاز (یا اتمسفر)، برابر مساحتی که بر آن تأثیر می گذارد. دو نیرو در جهت مخالف عمل می کنند و پیستون در هر طرف دارای مساحت یکسانی است، به این معنی که دو فشار باید برابر باشند. به همین دلیل است که گازهای داخل ظروف به همان فشار هوای بیرون می رسند - حجم گاز تا زمانی که نیروهای وارد بر ظرف متعادل شوند تنظیم می شود.

- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3265-
سپاس: 5494
- جنسیت:
تماس:
Re: تاثیر ارتفاع در فشار گاز در یک ظرف سربسته طویل
البته اگر نیروهای دیگری غیر از فشار روی دیواره کانتینر وارد شود، فشارها برابر نخواهد بود. به همین دلیل است که می توان یک خلاء (جزئی) در داخل یک ظرف سفت ایجاد کرد. همچنین به همین دلیل است که هوای داخل بالون باد شده فشار بیشتری نسبت به هوای بیرون دارد - پوست بالون در معرض نیروی کششی و همچنین دو نیروی فشار است.
تغییر فشار گاز در هر ظرف شتاب دهنده
، ظرف حاوی مایعی با چگالی rho است و به ظرف شتابی به سمت راست داده می شود و بنابراین با در نظر گرفتن این که هر قسمت مایع نیز شتابی مشابه ظرف ظرف دارد، می توانیم تغییرات فشار را دریابیم. با استفاده از قوانین نیوتن در مورد موتین. اما اگر گازی به جای مایع وجود داشته باشد، آیا فشار آن نیز مانند مایع متفاوت است؟ و اگر تغییر کند، آیا میتوانیم تغییر فشار داخل گاز را مانند همان روشی که در مورد مایع فهمیدیم، بفهمیم؟ از آنجایی که گاز و مایعات هر دو سیال هستند و خواص مشترک زیادی دارند. و هم مایع و هم گاز در این زمینه باید ایده آل فرض شوند. و ظرفی که گاز در آن نگهداری می شود کاملا بسته است.پاسخ کوتاه "بله" است. فشار گاز/مایع در قسمت های مختلف ظرف خواهد بود
$\Delta{P} = \rho g \Delta{h} + \rho a \Delta{l}$
(به هر دو موقعیت x و y در ظرف بستگی دارد).
توجه داشته باشید، اثرات گرانش و "حرکت با شتاب" بسیار شبیه هستند. در واقع آنها غیرقابل تشخیص هستند (یعنی "اصل هم ارزی").
فشار دیواره های یک ظرف سیلندر چقدر است
بنابراین، معادله فشار $p=F/A$ است.
من در یک ویدیو دیدم که فشاری که در یک منطقه وارد می شود همان فشاری است که به دیواره یک ظرف وارد می شود.
بنابراین برای فهمیدن فشار وارد شده به دیواره سیلندر باید مساحت پایه بالای سیلندر را بدانم.
شعاع قاعده بالا 1.85 سانتی متر است.
معادله محاسبه مساحت $(\pi r^2)$است. سپس، $\pi \cdot 1.85^2$، با $10.75210086\ cm^3$ به من بدهید.
من این اطلاعات را روی معادله فشار p = 1 نیوتن / 10.75210086 cm³ قرار دادم، که به من $0.09300507994\ Pa$ می دهد.
مراحلی که میزنم درسته و نتیجه درسته؟
پس چگونه کار می کند؟، به این معنا که من ارتفاع سیلندر را جایی نمی گذارم، و با توجه به آنچه قبلاً در مورد فشار روی دیوارها گفتم، آیا واقعاً به طور مساوی روی دیواره سیلندر اعمال می شود؟ حتی اگر ارتفاع سیلندر بزرگ باشد؟0
من فکر می کنم شما در مورد نحوه عملکرد فشار کمی گیج شده اید. اجازه دهید سعی کنم و مسائل را روشن کنم.
یک سیلندر حاوی یک سیال است (گاز یا مایع، در اینجا با چگالی صفر!). فشار بیرونی ناچیز در نظر گرفته می شود (a≈0) یک پیستون بی وزن که کاملا آب بندی شده است، آن را می بندد:
فشار
نیروی F بر روی پیستون وارد می شود که دارای مقطع A است.
فشار داخل ظرف، که در همه جهات منتقل می شود، به وسیله:
p=F/A
نیروی وارد شده به هر قسمت از دیوارها عبارتند از:
F(S)=pS
که در آن S مساحت سطح آن قسمت از دیواره سیلندر است.
! اگر چگالی سیال غیر صفر باشد، باید فشار هیدرواستاتیک را در نظر گرفت.
اگر چگالی سیال ρ باشد، برای لایهای در فاصله h از پیستون، قانون پاسکال به ما میگوید که ph فشار هیدرواستاتیکی به صورت زیر داده میشود:
$p_h=\rho gh$
و فشار کل در آن سطح خواهد بود:
$p_t=\rho gh+\frac{F}{A}$
چرا فشار و حجم گاز در ظرف باز همیشه ثابت است؟فشار سعی می کند حجم را افزایش دهد. با فرض اینکه فشار اتمسفر در اینجا تغییر نمی کند و فشار کل داخل جسم با گرم کردن گاز داخل آن دو برابر می شود، منجر به انبساط جسم (اگر بتوان آن را کشید) زمانی که شروع به افزایش حجم کرد فشار روی دیواره ها شروع به کاهش می کند (زیرا افزایش حجم تعداد مولکولهایی که به ناحیه خاصی از کانتینر برخورد میکنند کاهش مییابد) این امر ادامه مییابد تا فشار واحد مانند اتمسفر شود. این باعث دو برابر شدن حجم جسم می شود. در اینجا فشار ثابت می ماند در حالی که حجم تغییر می کند. اما از آنجایی که ظرف در این حالت باز است، نمی توانید حجم بیشتری به دست آورید و فقط به ظرف بستگی دارد
فشار داخل ظرف هنگام بسته شدن ظرف
فرض کنید ظرفی وجود دارد که درب آن باز است و در ته یک اقیانوس نشسته است. فشار در ته ظرف به ستون آب بالای آن با فرض فشار استاتیک بستگی دارد. حالا اگر درب ظرف را ببندم فشار ته ظرف کم می شود؟ من فکر می کنم این کار خواهد شد زیرا ارتفاع ستون آب کاهش یافته است. درپوش تقریباً تمام وزن ستون آب بالای آن را تحمل می کند. می دانم سوال احمقانه ای است اما نمی دانم کجا اشتباه می کنم. من چیزی را از دست داده ام؟! توضیحات تصویر را اینجا وارد کنید با عرض پوزش برای ترسیم بد. P فشار مورد نیاز در نزدیکی کف ظرف پس از بستن درب آن است. فرض کنید فشار فقط به دلیل وزن ستون آب است.
ما اغلب فشار را در کف یک سیال (چگال) ساده می کنیم تا P=ρgh باشد. اما این فقط فشار اضافی در پایین به دلیل سیال است. اگر فشاری در بالای سیال وجود داشته باشد، آن نیز به آن اضافه می شود.
بنابراین فشار در پایین $P_{bottom} = \rho gh + P_{top}$ است
هنگامی که درب را می بندید، ستون سیال در جعبه کوتاه تر است، اما فشار وارد شده به بالای ستون به دلیل سفتی درب افزایش می یابد. فشار در پایین بدون تغییر باقی می ماند.وقتی درب را وصل می کنید فشار بالا و پایین آن یکسان است، در حالت تعادل است. فشار داخل ظرف با بسته شدن درب آن تغییر نمی کند. بله، ستون آب بالای پایه ظرف کوچک شده است، اما بالای آن ستون کوچک به اندازه ظرف در فشار بالا است، در فشار سطحی نیست.برای یک درب کاملاً سفت و سخت، وزن تمام آب بالای آن از طریق ظرف به کف منتقل می شود. بنابراین، فشار ته ظرف همان فشاری خواهد بود که اگر ظرف خارج از آب بود.
برای یک درب کاملاً الاستیک، فشار به طور کامل به ظرف منتقل می شود و فشار در پایین ظرف مانند فشار بیرون ظرف در همان عمق خواهد بود.
برای ظروف واقعی در بین دو حالت فوق، بر اساس میزان انتقال از طریق درب و میزان انتقال از طریق ظرف، فشار متوسط دو مورد فوق خواهد بود.
اختلاف فشار گاز در یک ظرف بسته در فاصله معینی از زمین چقدر است؟اگر من یک ظرف بسته با ارتفاع معین (h) داشته باشم که در فاصله معینی از مرکز زمین (ro) قرار دارد، اختلاف فشار در بالای ظرف با پایین چقدر خواهد بود؟
که فشار سیال P=ρhg است که ρ چگالی سیال، h ارتفاع مایع بالا و g نیروی گرانش است.
با این حال، من فکر می کنم که به یک ظرف باز اشاره دارد و همچنین از آنجایی که قد من ممکن است به اندازه 1 متر و $10^7$ متر باشد، من کاملاً مطمئن نیستم که بتوانم از این فرمول به عنوان g میتواند به طور قابل توجهی استفاده کنم که به نظر می رسد. برای باطل کردن محاسبه جرمی که برای رسیدن به آن فرمول استفاده شد $F = m g \rightarrow F = (\rho V) g \rightarrow F = (\rho A h) g$، زیرا چگالی می تواند بسیار بیشتر از ارتفاع باشد. همچنین، ρ به دما، فشار و حجم بستگی دارد، بنابراین این موضوع را پیچیدهتر میکند، بنابراین من حتی نمیدانم از کجا شروع کنم معادله حاکم بر فشار هیدرواستاتیک (هوا حرکت نمی کند) است
$\frac{dp} {dz} = - \rho g$
بنابراین اگر چگالی و گرانش خود را تابعی از z بدانید، می توانید فشار را بفهمید. از طرف دیگر، میتوانید فرض کنید که هوا یک گاز ایدهآل است، و برخی فرضیات اضافی دیگر در مورد نحوه رفتار هوا در حین بالا رفتن از اتمسفر ایجاد کنید و آن را محاسبه کنید.
فشار بالای یک لوله مهر و موم شده که از آب خارج می شود چقدر است؟آیا فشار اتمسفر در یک ظرف دربسته با فشار اتمسفر اطراف (1 بار در سطح دریا) یکسان است؟
لوله ای را در نظر بگیرید که دو سر آن باز است و یک سر آن در آب فرو رفته است (مانند یک پیپت در آزمایشگاه شیمی). حال اگر سر دیگر آن را با انگشت شست ببندیم و از آب بیرون بکشیم، سطح آب لوله از سطح آب اطراف بالاتر خواهد بود.
اگر بگوییم به این دلیل است که جوی که آب را در لوله به بالا فشار می دهد مانند جوی است که هوای باقی مانده در لوله به سمت پایین فشار می آورد، آیا آب به دلیل وزن خود به عنوان فشار رو به بالا و پایین نمی ریزد. متعادل است؟ من توضیحی در مورد کل فرآیند می خواهم که وزن آب را با فشار بالا و پایین جو مقایسه می کند.اجازه دهید ابتدا چند متغیر را تعریف کنیم. فرض کنید که طول ستون هوایی که در لوله بین سطح آب و انگشت شست خود حبس می کنید h0 است و در ابتدا با فشار هوای اطراف آن را P0 می نامیم. همچنین اجازه دهید سطح مقطع لوله را A تعریف کنیم. همانطور که لوله را از آب بیرون می آورید، سطح آب در لوله از سطح آب اطراف بالاتر می رود و فشار در پایین این ستون آب افزایش می یابد. توسط داده خواهد شد
$P_0=P_t+\rho g h_w,$
که در آن Pt فشار حجم هوای محبوس شده توسط انگشت شست شما، ρ چگالی جرم آب، g شتاب گرانشی در سطح زمین، و hw اختلاف ارتفاع بین آب در لوله و لوله است. آب اطراف عبارت دوم در سمت راست یک معادله استاندارد از استاتیک سیال است. از همین حالا میبینید که فشار در بالای لوله دیگر نمیتواند یکسان باشد، همانطور که فکر میکردید.
می توانیم از قانون گاز ایده آل برای بازنویسی عبارت اول در سمت راست استفاده کنیم
$P_tV_t=P_0V_0\qquad\Rightarrow\qquad P_t=P_0\frac{V_0}{V_t}$
اکنون حجم هوای بالای لوله قبل از شروع به کشیدن آن با $V_0=Ah_0$ داده می شود، اما با کشیدن آن فشار و حجم به$V_t=Ah_t$ تغییر می کند. بنابراین، قرار دادن تمام این اطلاعات در اولین معادله ای که به دست می آوریم
$P_0=P_0\frac{h_0}{h_t}+\rho g h_w$آخرین چیزی که باید از آن مراقبت کنیم این است که $h_t$ را با چیزی که واقعاً می دانیم جایگزین کنیم. یعنی ارتفاعی که لوله را به سمت بالا می کشیم که آن را hs می نامیم و با$h_s=h_t+h_w$داده می شود. چسباندن این به معادله بالا نتیجه می دهد
$P_0=P_0\frac{h_0}{(h_s-h_w)}+\rho g h_w$
حل این معادله برای $h_w$ به دست می دهد
$h_w=\frac{1}{2\rho g}\left(P_0+\rho g h_s+\sqrt{P_0^2+(\rho gh_s)^2+P_0\rho g(4h_0-h_s)}\right).$من این معادله را در زیر برای مقادیر متفاوت h0 رسم کرده ام. توجه داشته باشید که حداکثر ارتفاعی وجود دارد که می توانید با این روش آب را به آن بکشید، این ارتفاعی است که فشار در لوله به صفر می رسد.
در نهایت، از آنجایی که سوال شما در واقع در مورد فشار در لوله بود، میتوانیم معادلات بالا را برای حل فشار در لوله زیر انگشت شستتان دوباره مرتب کنیم.
$P_t=P_0-\rho gh_w=\frac{1}{2}\left(P_0-\rho g h_s-\sqrt{P_0^2+(\rho gh_s)^2+P_0\rho g(4h_0-h_s)}\right).$این معادله
آیا فشار هوای داخل جعبه پس از آب بندی ثابت باقی می ماند؟فرض کنید فشار خارج از جعبه مهر و موم شده 1 اتمسفر باشد. فکر می کنم فشار داخل جعبه در 1 اتمسفر یکسان باشد. اما چرا؟
آیا وقتی جعبه را مهر و موم می کنم ستون غول پیکر هوا در بالا باعث فشار نمی شود؟پاسخ کوتاه: با فرض اینکه شما به سادگی جعبه را مهر و موم کرده اید در حالی که هوای داخل در فشار اتمسفر است، بله، به همین شکل باقی می ماند.
چرا: بدون وارد شدن زیاد به علف های هرز: از نظر میکروسکوپی، فشار نتیجه جهش مولکول های کوچک هوا به سطح است. در این حالت، سطح کنار یک جعبه است. جهش هر مولکول مقدار کمی نیرو وارد می کند. اگر ذرات تقریباً مساوی در یک زمان معین به دو طرف آن سمت جعبه بپرند، طرف در هیچ جهتی حرکت نمی کند.
اگر به سادگی یک بسته هوا را در داخل یک مرز محصور کنیم بدون اینکه آن را فشار دهیم یا کاری برای آن انجام دهیم، همان تعداد ذرات در آن حجم هستند که قبلاً وجود دارد و به طور متوسط به همان سرعت به داخل و خارج هر سمت معین برخورد می کنند. مانند قبل (یا عبور از یک مرز اگر هیچ مانع فیزیکی برای متوقف کردن آنها وجود ندارد). ذرات منفرد قادر به ورود یا خروج از بسته نخواهند بود، اما از آنجایی که میانگین تعداد ذرات جهنده به طرفین ثابت می ماند، فشار یکسانی دریافت می کنیم.
تعداد ذرات که به طرف جهش می کنند بستگی به تعداد ذرات در حجم دارد. بنابراین ذرات بیشتر -> جهش بیشتر -> فشار بیشتر. بنابراین اگر فشار یکسانی در داخل و خارج داشته باشیم، تقریباً تعداد جهشها در هر دو طرف یکسان است، بنابراین طرفها به سمت داخل یا خارج برآمده نمیشوند. برای یک ریاضی کوچک که این موضوع را تأیید می کند، به پایین تر مراجعه کنید.
از آنجایی که خود دو طرف جعبه فقط به جهش های هر دو طرف واکنش نشان می دهند، ستون هوا همچنان روی جعبه سنگینی می کند، اما به خاطر داشته باشید که جعبه سعی می کند هوای داخل آن و آن هوا را نیز "وزن" کند. درون فشار به عقب است، که جعبه را نگه می دارد، که هوا را نگه می دارد (این قانون سوم نیوتن است "هر عملی یک واکنش برابر و مخالف دارد").
بله، اتمسفر حداقل از بالا به جعبه فشار می آورد (و احتمالاً کناره ها نیز، با فرض اینکه در معرض جو هستند). اما فراموش نکنید که هوای داخل جعبه نیز به طرفین جعبه فشار وارد می کند و نیروی درونی هوای بیرون را متعادل می کند.
در نظر بگیرید که هر بسته هوا از هر طرف "جعبه" شده است. ستون هوا به سمت پایین فشار میآورد، اما بسته نمیتواند به جایی برود، زیرا از قبل هوا در آن مکانها وجود دارد که مانع از ورود آن به آن فضاها میشود. سایر بسته های هوا نیز به همین ترتیب در جعبه قرار دارند، بنابراین آنها واقعاً نمی توانند به جایی بروند. البته، ذرات جداگانه می توانند بین این بسته ها ارتباط برقرار کنند، زیرا مرز واقعی وجود ندارد. برای هر ذره ای که به یک سمت می رود، ذره دیگری به داخل می لغزد. نقطه خالی، احتمالاً از یک بسته دیگر. اگر یک مرز واقعی به طور ناگهانی اتفاق بیفتد (مثلاً، یک کلاه بر روی یک لاستیک پنچر قرار دهیم)، ذرات به سادگی نمی توانند بین بسته ها حرکت کنند، اما تعداد کلی ذرات در یک بسته به همان صورت باقی می ماند.
حقیقت:
$\text{Area of the side of the inside of the box} = \text{Area of the side on the outside of the box}$نیرو=فشار∗منطقه
از آنجایی که$A_\text{inside} = A_\text{outside}$، پس
$F_\text{inside} = F_\text{outside}$
برای هر طرف این بدان معناست که جعبه قرار نیست فرو بریزد زیرا نیروهای هوای داخل و خارج متعادل می شوند.
اگر میپرسید چه چیزی ستون هوای بیرون از جعبه را نگه میدارد، اگر 1 Atm هوا را در داخل آن ببندید، پس هوای داخل آن چیزی است که آن را پشتیبانی میکند (تا آنجا که ستون هوا اهمیت میدهد اساساً مانند یک بلوک جامد است) . خود جعبه فقط شامل حجم است و به خودی خود هیچ پشتیبانی در اینجا ارائه نمی دهد.
اگر جعبه با خلاء در داخل (0 Atm) مهر و موم شده بود و جعبه آنقدر محکم بود که فرو نریزد، به این معنی است که مواد فیزیکی خود جعبه ستون هوا را پشتیبانی می کند. آن وضعیت کمی متفاوت است. شما باید یک جعبه بسیار قوی داشته باشید،
قبل از اینکه جعبه را آب بندی کنید، هوای داخل و خارج می توانست با هم ارتباط برقرار کند (امواج فشار را مبادله می کند) و بنابراین فشار در همه جا 1 اتمسفر بود. اگر اختلافات دقیقه ای وجود داشت، آنها امواج فشار را رد و بدل می کردند و گاز حرکت می کرد تا یکسان شود.
با این حال، هنگامی که جعبه را مهر و موم می کنید، هر دو از 1 اتمسفر شروع می شوند، اما هیچ چیز به طور فعال آنها را ثابت نگه نمی دارد (اگر دیوارها سفت و سخت باشند)، زیرا امواج فشار دیگر نمی توانند از مرز عبور کنند. اگر تغییری رخ دهد، مانند گرمایش یا سرمایش جعبه، یا در غیر این صورت اتمسفر محیط از 1 atm به 0.999 atm به دلیل آب و هوا کاهش یابد، این دو فشار متفاوت خواهند بود. این مورد برای هر مخزن هوا، مخزن غواصی یا حتی خانه شما تا حدی صدق می کند. سیستم های تهویه باید طوری طراحی شوند که به داخل و خارج اجازه دهند تا هوا را با تغییرات دما و آب و هوا به طور مناسب مبادله کنند، در غیر این صورت عدم تعادل فشار ایجاد می شود که می تواند دیوارها یا ساختارهای دیگر را بشکند.
تغییر فشار گاز در هر ظرف شتاب دهنده
، ظرف حاوی مایعی با چگالی rho است و به ظرف شتابی به سمت راست داده می شود و بنابراین با در نظر گرفتن این که هر قسمت مایع نیز شتابی مشابه ظرف ظرف دارد، می توانیم تغییرات فشار را دریابیم. با استفاده از قوانین نیوتن در مورد موتین. اما اگر گازی به جای مایع وجود داشته باشد، آیا فشار آن نیز مانند مایع متفاوت است؟ و اگر تغییر کند، آیا میتوانیم تغییر فشار داخل گاز را مانند همان روشی که در مورد مایع فهمیدیم، بفهمیم؟ از آنجایی که گاز و مایعات هر دو سیال هستند و خواص مشترک زیادی دارند. و هم مایع و هم گاز در این زمینه باید ایده آل فرض شوند. و ظرفی که گاز در آن نگهداری می شود کاملا بسته است.پاسخ کوتاه "بله" است. فشار گاز/مایع در قسمت های مختلف ظرف خواهد بود
$\Delta{P} = \rho g \Delta{h} + \rho a \Delta{l}$
(به هر دو موقعیت x و y در ظرف بستگی دارد).
توجه داشته باشید، اثرات گرانش و "حرکت با شتاب" بسیار شبیه هستند. در واقع آنها غیرقابل تشخیص هستند (یعنی "اصل هم ارزی").
فشار دیواره های یک ظرف سیلندر چقدر است
بنابراین، معادله فشار $p=F/A$ است.
من در یک ویدیو دیدم که فشاری که در یک منطقه وارد می شود همان فشاری است که به دیواره یک ظرف وارد می شود.
بنابراین برای فهمیدن فشار وارد شده به دیواره سیلندر باید مساحت پایه بالای سیلندر را بدانم.
شعاع قاعده بالا 1.85 سانتی متر است.
معادله محاسبه مساحت $(\pi r^2)$است. سپس، $\pi \cdot 1.85^2$، با $10.75210086\ cm^3$ به من بدهید.
من این اطلاعات را روی معادله فشار p = 1 نیوتن / 10.75210086 cm³ قرار دادم، که به من $0.09300507994\ Pa$ می دهد.
مراحلی که میزنم درسته و نتیجه درسته؟
پس چگونه کار می کند؟، به این معنا که من ارتفاع سیلندر را جایی نمی گذارم، و با توجه به آنچه قبلاً در مورد فشار روی دیوارها گفتم، آیا واقعاً به طور مساوی روی دیواره سیلندر اعمال می شود؟ حتی اگر ارتفاع سیلندر بزرگ باشد؟0
من فکر می کنم شما در مورد نحوه عملکرد فشار کمی گیج شده اید. اجازه دهید سعی کنم و مسائل را روشن کنم.
یک سیلندر حاوی یک سیال است (گاز یا مایع، در اینجا با چگالی صفر!). فشار بیرونی ناچیز در نظر گرفته می شود (a≈0) یک پیستون بی وزن که کاملا آب بندی شده است، آن را می بندد:
فشار
نیروی F بر روی پیستون وارد می شود که دارای مقطع A است.
فشار داخل ظرف، که در همه جهات منتقل می شود، به وسیله:
p=F/A
نیروی وارد شده به هر قسمت از دیوارها عبارتند از:
F(S)=pS
که در آن S مساحت سطح آن قسمت از دیواره سیلندر است.
! اگر چگالی سیال غیر صفر باشد، باید فشار هیدرواستاتیک را در نظر گرفت.
اگر چگالی سیال ρ باشد، برای لایهای در فاصله h از پیستون، قانون پاسکال به ما میگوید که ph فشار هیدرواستاتیکی به صورت زیر داده میشود:
$p_h=\rho gh$
و فشار کل در آن سطح خواهد بود:
$p_t=\rho gh+\frac{F}{A}$
چرا فشار و حجم گاز در ظرف باز همیشه ثابت است؟فشار سعی می کند حجم را افزایش دهد. با فرض اینکه فشار اتمسفر در اینجا تغییر نمی کند و فشار کل داخل جسم با گرم کردن گاز داخل آن دو برابر می شود، منجر به انبساط جسم (اگر بتوان آن را کشید) زمانی که شروع به افزایش حجم کرد فشار روی دیواره ها شروع به کاهش می کند (زیرا افزایش حجم تعداد مولکولهایی که به ناحیه خاصی از کانتینر برخورد میکنند کاهش مییابد) این امر ادامه مییابد تا فشار واحد مانند اتمسفر شود. این باعث دو برابر شدن حجم جسم می شود. در اینجا فشار ثابت می ماند در حالی که حجم تغییر می کند. اما از آنجایی که ظرف در این حالت باز است، نمی توانید حجم بیشتری به دست آورید و فقط به ظرف بستگی دارد
فشار داخل ظرف هنگام بسته شدن ظرف
فرض کنید ظرفی وجود دارد که درب آن باز است و در ته یک اقیانوس نشسته است. فشار در ته ظرف به ستون آب بالای آن با فرض فشار استاتیک بستگی دارد. حالا اگر درب ظرف را ببندم فشار ته ظرف کم می شود؟ من فکر می کنم این کار خواهد شد زیرا ارتفاع ستون آب کاهش یافته است. درپوش تقریباً تمام وزن ستون آب بالای آن را تحمل می کند. می دانم سوال احمقانه ای است اما نمی دانم کجا اشتباه می کنم. من چیزی را از دست داده ام؟! توضیحات تصویر را اینجا وارد کنید با عرض پوزش برای ترسیم بد. P فشار مورد نیاز در نزدیکی کف ظرف پس از بستن درب آن است. فرض کنید فشار فقط به دلیل وزن ستون آب است.

ما اغلب فشار را در کف یک سیال (چگال) ساده می کنیم تا P=ρgh باشد. اما این فقط فشار اضافی در پایین به دلیل سیال است. اگر فشاری در بالای سیال وجود داشته باشد، آن نیز به آن اضافه می شود.
بنابراین فشار در پایین $P_{bottom} = \rho gh + P_{top}$ است
هنگامی که درب را می بندید، ستون سیال در جعبه کوتاه تر است، اما فشار وارد شده به بالای ستون به دلیل سفتی درب افزایش می یابد. فشار در پایین بدون تغییر باقی می ماند.وقتی درب را وصل می کنید فشار بالا و پایین آن یکسان است، در حالت تعادل است. فشار داخل ظرف با بسته شدن درب آن تغییر نمی کند. بله، ستون آب بالای پایه ظرف کوچک شده است، اما بالای آن ستون کوچک به اندازه ظرف در فشار بالا است، در فشار سطحی نیست.برای یک درب کاملاً سفت و سخت، وزن تمام آب بالای آن از طریق ظرف به کف منتقل می شود. بنابراین، فشار ته ظرف همان فشاری خواهد بود که اگر ظرف خارج از آب بود.
برای یک درب کاملاً الاستیک، فشار به طور کامل به ظرف منتقل می شود و فشار در پایین ظرف مانند فشار بیرون ظرف در همان عمق خواهد بود.
برای ظروف واقعی در بین دو حالت فوق، بر اساس میزان انتقال از طریق درب و میزان انتقال از طریق ظرف، فشار متوسط دو مورد فوق خواهد بود.
اختلاف فشار گاز در یک ظرف بسته در فاصله معینی از زمین چقدر است؟اگر من یک ظرف بسته با ارتفاع معین (h) داشته باشم که در فاصله معینی از مرکز زمین (ro) قرار دارد، اختلاف فشار در بالای ظرف با پایین چقدر خواهد بود؟
که فشار سیال P=ρhg است که ρ چگالی سیال، h ارتفاع مایع بالا و g نیروی گرانش است.
با این حال، من فکر می کنم که به یک ظرف باز اشاره دارد و همچنین از آنجایی که قد من ممکن است به اندازه 1 متر و $10^7$ متر باشد، من کاملاً مطمئن نیستم که بتوانم از این فرمول به عنوان g میتواند به طور قابل توجهی استفاده کنم که به نظر می رسد. برای باطل کردن محاسبه جرمی که برای رسیدن به آن فرمول استفاده شد $F = m g \rightarrow F = (\rho V) g \rightarrow F = (\rho A h) g$، زیرا چگالی می تواند بسیار بیشتر از ارتفاع باشد. همچنین، ρ به دما، فشار و حجم بستگی دارد، بنابراین این موضوع را پیچیدهتر میکند، بنابراین من حتی نمیدانم از کجا شروع کنم معادله حاکم بر فشار هیدرواستاتیک (هوا حرکت نمی کند) است
$\frac{dp} {dz} = - \rho g$
بنابراین اگر چگالی و گرانش خود را تابعی از z بدانید، می توانید فشار را بفهمید. از طرف دیگر، میتوانید فرض کنید که هوا یک گاز ایدهآل است، و برخی فرضیات اضافی دیگر در مورد نحوه رفتار هوا در حین بالا رفتن از اتمسفر ایجاد کنید و آن را محاسبه کنید.
فشار بالای یک لوله مهر و موم شده که از آب خارج می شود چقدر است؟آیا فشار اتمسفر در یک ظرف دربسته با فشار اتمسفر اطراف (1 بار در سطح دریا) یکسان است؟
لوله ای را در نظر بگیرید که دو سر آن باز است و یک سر آن در آب فرو رفته است (مانند یک پیپت در آزمایشگاه شیمی). حال اگر سر دیگر آن را با انگشت شست ببندیم و از آب بیرون بکشیم، سطح آب لوله از سطح آب اطراف بالاتر خواهد بود.
اگر بگوییم به این دلیل است که جوی که آب را در لوله به بالا فشار می دهد مانند جوی است که هوای باقی مانده در لوله به سمت پایین فشار می آورد، آیا آب به دلیل وزن خود به عنوان فشار رو به بالا و پایین نمی ریزد. متعادل است؟ من توضیحی در مورد کل فرآیند می خواهم که وزن آب را با فشار بالا و پایین جو مقایسه می کند.اجازه دهید ابتدا چند متغیر را تعریف کنیم. فرض کنید که طول ستون هوایی که در لوله بین سطح آب و انگشت شست خود حبس می کنید h0 است و در ابتدا با فشار هوای اطراف آن را P0 می نامیم. همچنین اجازه دهید سطح مقطع لوله را A تعریف کنیم. همانطور که لوله را از آب بیرون می آورید، سطح آب در لوله از سطح آب اطراف بالاتر می رود و فشار در پایین این ستون آب افزایش می یابد. توسط داده خواهد شد
$P_0=P_t+\rho g h_w,$
که در آن Pt فشار حجم هوای محبوس شده توسط انگشت شست شما، ρ چگالی جرم آب، g شتاب گرانشی در سطح زمین، و hw اختلاف ارتفاع بین آب در لوله و لوله است. آب اطراف عبارت دوم در سمت راست یک معادله استاندارد از استاتیک سیال است. از همین حالا میبینید که فشار در بالای لوله دیگر نمیتواند یکسان باشد، همانطور که فکر میکردید.
می توانیم از قانون گاز ایده آل برای بازنویسی عبارت اول در سمت راست استفاده کنیم
$P_tV_t=P_0V_0\qquad\Rightarrow\qquad P_t=P_0\frac{V_0}{V_t}$
اکنون حجم هوای بالای لوله قبل از شروع به کشیدن آن با $V_0=Ah_0$ داده می شود، اما با کشیدن آن فشار و حجم به$V_t=Ah_t$ تغییر می کند. بنابراین، قرار دادن تمام این اطلاعات در اولین معادله ای که به دست می آوریم
$P_0=P_0\frac{h_0}{h_t}+\rho g h_w$آخرین چیزی که باید از آن مراقبت کنیم این است که $h_t$ را با چیزی که واقعاً می دانیم جایگزین کنیم. یعنی ارتفاعی که لوله را به سمت بالا می کشیم که آن را hs می نامیم و با$h_s=h_t+h_w$داده می شود. چسباندن این به معادله بالا نتیجه می دهد
$P_0=P_0\frac{h_0}{(h_s-h_w)}+\rho g h_w$
حل این معادله برای $h_w$ به دست می دهد
$h_w=\frac{1}{2\rho g}\left(P_0+\rho g h_s+\sqrt{P_0^2+(\rho gh_s)^2+P_0\rho g(4h_0-h_s)}\right).$من این معادله را در زیر برای مقادیر متفاوت h0 رسم کرده ام. توجه داشته باشید که حداکثر ارتفاعی وجود دارد که می توانید با این روش آب را به آن بکشید، این ارتفاعی است که فشار در لوله به صفر می رسد.
در نهایت، از آنجایی که سوال شما در واقع در مورد فشار در لوله بود، میتوانیم معادلات بالا را برای حل فشار در لوله زیر انگشت شستتان دوباره مرتب کنیم.
$P_t=P_0-\rho gh_w=\frac{1}{2}\left(P_0-\rho g h_s-\sqrt{P_0^2+(\rho gh_s)^2+P_0\rho g(4h_0-h_s)}\right).$این معادله
آیا فشار هوای داخل جعبه پس از آب بندی ثابت باقی می ماند؟فرض کنید فشار خارج از جعبه مهر و موم شده 1 اتمسفر باشد. فکر می کنم فشار داخل جعبه در 1 اتمسفر یکسان باشد. اما چرا؟
آیا وقتی جعبه را مهر و موم می کنم ستون غول پیکر هوا در بالا باعث فشار نمی شود؟پاسخ کوتاه: با فرض اینکه شما به سادگی جعبه را مهر و موم کرده اید در حالی که هوای داخل در فشار اتمسفر است، بله، به همین شکل باقی می ماند.
چرا: بدون وارد شدن زیاد به علف های هرز: از نظر میکروسکوپی، فشار نتیجه جهش مولکول های کوچک هوا به سطح است. در این حالت، سطح کنار یک جعبه است. جهش هر مولکول مقدار کمی نیرو وارد می کند. اگر ذرات تقریباً مساوی در یک زمان معین به دو طرف آن سمت جعبه بپرند، طرف در هیچ جهتی حرکت نمی کند.
اگر به سادگی یک بسته هوا را در داخل یک مرز محصور کنیم بدون اینکه آن را فشار دهیم یا کاری برای آن انجام دهیم، همان تعداد ذرات در آن حجم هستند که قبلاً وجود دارد و به طور متوسط به همان سرعت به داخل و خارج هر سمت معین برخورد می کنند. مانند قبل (یا عبور از یک مرز اگر هیچ مانع فیزیکی برای متوقف کردن آنها وجود ندارد). ذرات منفرد قادر به ورود یا خروج از بسته نخواهند بود، اما از آنجایی که میانگین تعداد ذرات جهنده به طرفین ثابت می ماند، فشار یکسانی دریافت می کنیم.
تعداد ذرات که به طرف جهش می کنند بستگی به تعداد ذرات در حجم دارد. بنابراین ذرات بیشتر -> جهش بیشتر -> فشار بیشتر. بنابراین اگر فشار یکسانی در داخل و خارج داشته باشیم، تقریباً تعداد جهشها در هر دو طرف یکسان است، بنابراین طرفها به سمت داخل یا خارج برآمده نمیشوند. برای یک ریاضی کوچک که این موضوع را تأیید می کند، به پایین تر مراجعه کنید.
از آنجایی که خود دو طرف جعبه فقط به جهش های هر دو طرف واکنش نشان می دهند، ستون هوا همچنان روی جعبه سنگینی می کند، اما به خاطر داشته باشید که جعبه سعی می کند هوای داخل آن و آن هوا را نیز "وزن" کند. درون فشار به عقب است، که جعبه را نگه می دارد، که هوا را نگه می دارد (این قانون سوم نیوتن است "هر عملی یک واکنش برابر و مخالف دارد").
بله، اتمسفر حداقل از بالا به جعبه فشار می آورد (و احتمالاً کناره ها نیز، با فرض اینکه در معرض جو هستند). اما فراموش نکنید که هوای داخل جعبه نیز به طرفین جعبه فشار وارد می کند و نیروی درونی هوای بیرون را متعادل می کند.
در نظر بگیرید که هر بسته هوا از هر طرف "جعبه" شده است. ستون هوا به سمت پایین فشار میآورد، اما بسته نمیتواند به جایی برود، زیرا از قبل هوا در آن مکانها وجود دارد که مانع از ورود آن به آن فضاها میشود. سایر بسته های هوا نیز به همین ترتیب در جعبه قرار دارند، بنابراین آنها واقعاً نمی توانند به جایی بروند. البته، ذرات جداگانه می توانند بین این بسته ها ارتباط برقرار کنند، زیرا مرز واقعی وجود ندارد. برای هر ذره ای که به یک سمت می رود، ذره دیگری به داخل می لغزد. نقطه خالی، احتمالاً از یک بسته دیگر. اگر یک مرز واقعی به طور ناگهانی اتفاق بیفتد (مثلاً، یک کلاه بر روی یک لاستیک پنچر قرار دهیم)، ذرات به سادگی نمی توانند بین بسته ها حرکت کنند، اما تعداد کلی ذرات در یک بسته به همان صورت باقی می ماند.
حقیقت:
$\text{Area of the side of the inside of the box} = \text{Area of the side on the outside of the box}$نیرو=فشار∗منطقه
از آنجایی که$A_\text{inside} = A_\text{outside}$، پس
$F_\text{inside} = F_\text{outside}$
برای هر طرف این بدان معناست که جعبه قرار نیست فرو بریزد زیرا نیروهای هوای داخل و خارج متعادل می شوند.
اگر میپرسید چه چیزی ستون هوای بیرون از جعبه را نگه میدارد، اگر 1 Atm هوا را در داخل آن ببندید، پس هوای داخل آن چیزی است که آن را پشتیبانی میکند (تا آنجا که ستون هوا اهمیت میدهد اساساً مانند یک بلوک جامد است) . خود جعبه فقط شامل حجم است و به خودی خود هیچ پشتیبانی در اینجا ارائه نمی دهد.
اگر جعبه با خلاء در داخل (0 Atm) مهر و موم شده بود و جعبه آنقدر محکم بود که فرو نریزد، به این معنی است که مواد فیزیکی خود جعبه ستون هوا را پشتیبانی می کند. آن وضعیت کمی متفاوت است. شما باید یک جعبه بسیار قوی داشته باشید،
قبل از اینکه جعبه را آب بندی کنید، هوای داخل و خارج می توانست با هم ارتباط برقرار کند (امواج فشار را مبادله می کند) و بنابراین فشار در همه جا 1 اتمسفر بود. اگر اختلافات دقیقه ای وجود داشت، آنها امواج فشار را رد و بدل می کردند و گاز حرکت می کرد تا یکسان شود.
با این حال، هنگامی که جعبه را مهر و موم می کنید، هر دو از 1 اتمسفر شروع می شوند، اما هیچ چیز به طور فعال آنها را ثابت نگه نمی دارد (اگر دیوارها سفت و سخت باشند)، زیرا امواج فشار دیگر نمی توانند از مرز عبور کنند. اگر تغییری رخ دهد، مانند گرمایش یا سرمایش جعبه، یا در غیر این صورت اتمسفر محیط از 1 atm به 0.999 atm به دلیل آب و هوا کاهش یابد، این دو فشار متفاوت خواهند بود. این مورد برای هر مخزن هوا، مخزن غواصی یا حتی خانه شما تا حدی صدق می کند. سیستم های تهویه باید طوری طراحی شوند که به داخل و خارج اجازه دهند تا هوا را با تغییرات دما و آب و هوا به طور مناسب مبادله کنند، در غیر این صورت عدم تعادل فشار ایجاد می شود که می تواند دیوارها یا ساختارهای دیگر را بشکند.


