تصویر در آینه
- You-See
نام: U30
محل اقامت: تهران
عضویت : یکشنبه ۱۳۹۳/۵/۱۹ - ۱۹:۰۵
پست: 1280-
سپاس: 787
- جنسیت:
تماس:
Re: تصویر درآینه
تصویر در آینه وارون در محور z هست.
برای اطلاع بیشتر این رو ببینید
https://www.youtube.com/embed/1t4dOPxKgrY
برای اطلاع بیشتر این رو ببینید
https://www.youtube.com/embed/1t4dOPxKgrY
دوستای گلم حمایت کنید : https://cafebazaar.ir/app/com.nikanmehr.marmarxword/
- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3278-
سپاس: 5494
- جنسیت:
تماس:
Re: تصویر در آینه
به نظر من فوتون ها - ذرات نور - به سمت شیشه صاف جریان می یابند و از آن جامپینگ کرده. تصویر همه چیز جلوی آینه به عقب منعکس می شود و مسیری را که برای رسیدن به آنجا طی کرده است رفلکشن میده. هیچ چیز از چپ به راست یا بالا به پایین تغییر نمیکنه . در عوض، از جلو به عقب ریورس می شود.
شما فرض کردید که به صورت ورتیکال ریورس نیستید و می پرسید چرا ورتیکال ریورس نیستید.
چرا تصاویر آینه ای به صورت افقی چرخانده میشن اما ورتیکال نیستند؟چرابه نظر میرسه که آینه ها L و R را می چرخانند؟ بدن شما یک صفحه آینه ای در امتداد اکسیس Z داره. هنگامی که حول اکسیسZ خود می چرخید تقریباً به همان شکلی به نظر می رسید که گویی خود را در آینه می بینید. تفاوتها با دستان شما که دستی را تغییر دادهاند
توجه داشته باشید، اگر حول اکسیسY خود بچرخانید و با دست ایستاده باشید
بنابراین آینهها نیز نمیتوانند آن را به طرفین برگردانند در عوض یک عمل سیمتری به نام آینه را پیش میکشه. وقتی 180 درجه بچرخین در حال انجام یک عملیات سیمتری دیگر به نام روتیشن هستید به عنوان روتیشن دو برابری نیز شناخته میگن هیچ چیز ذاتا درست تر از روتیشن در مقابلسیمتری آینه وجود نداره
چرا تصویر روی یک آینه مسطح به صورت لترال ریورس است؟
چرا در آینه صفحه لترال اینورژن وجود دارد؟ لترال اینورژن این دلیله که در یک آینه مسطح تصویر به همان اندازه که جسم در مقابل آن قرار دارد پشت آینه است و جلوی تصویر و جلوی جسم رو به روی هم هستند.آینه ها از چپ به راست ریورس نمی شوند، از جلو به عقب بر می گردند. این را در نظر بگیریدوقتی در آینه به خود نگاه می کنیدبه نظر میرسه کهه رفلکشن شما شخص دیگری است که دقیقاً شبیه شماست که پشت یک تکه شیشه ایستادین در همان فاصله ای که از شیشه دارید و رو به روی شماست. نکته مهم اینجاست - 180 درجه حول ورتیکال اکسیس چرخید تا رو به شما باشد. حالا دست چپ او باید مقابل دست راست شما باشد و بالعکس. در واقع این فرض اشتباه است. بازتاب شما روتیشن 180 درجه ای انجام نداد. از جلو به عقب و بدون هیچ روتاری برعکس بود. مغز شما روتیشن 180 درجه ای را که فرض می کنید باید اتفاق افتاده باشد را از نظر مشاهده شده از جلو به عقب کم می کند و چه چیزی به دست می آورید؟ یک برگشت ظاهری از چپ به راست!اگر در درک جهت همه چیز مشکل دارید در اینجا یک توضیح دقیق بدم: آینه تخت دایره ای در صفحه z=0 (افقی)، $x^2+y^2\le1$ است. آینه کروی نیمکره ای است که با z>0، $x^2+y^2+z^2=1$ توصیف میشه. شما در داخل ایستاده ایدخوب دست شما در نقطه ای نزدیک به اکسیس قرار داره برای مثال، (0.01، 0، 0.2). کاری که آینه ها انجام میدن اینکه برای یک جسم در یک نقطه (x,y,z)، آینه تخت تصویری را در (x,y,-z) ایجاد می کند (این تصویر دارای عقربه مخالفه زیرا یک کوردینیت سیستم برگردانده شده. سپس آینه کروی آن تصویر را در (x,y,−z) می گیرد و تصویر دیگری را در (−x,−y,z) ایجاد میکنه این تصویر همان دست بودن شی اصلی را دارد. همچنین سمت راست به بالا است زیراکوردینیت z برگردانده نشده است. تصویر دست راست شما در (0.01، 0، 0.2) به عنوان یک دست راست دیگر در (-0.01، 0، 0.2) ظاهر میشه که در جهت مناسب برای دست دادن شما قرار دارد.سردرگمی کونوانسیون علامت ماتریس روتیشن.
در ماتریس روتیشن، چرا روتیشن اول و سوم را در خلاف جهت روتیشن دوم می چرخانیم، این کمی گمراه کننده هست
در این تصویر می توان توجه داشت که برای روتیشن x و Z عناصر غیر صفر یکسان هستند. اما برای Y روتیشن علامت (تتا) تغییر کرد.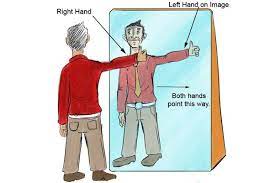
من فکر می کنم مسئله اصلی این است که شما سعی می کنید ماتریس های روتیشن خود را از چپ به راست بخونید. تغییرات علامت تصادفی به نظر میرسه اما در واقع به روشی معمولی روتیشن میکنه.
بیایید با این سوال شروع کنیم:
الف) اصلاً چرا منفی ها ظاهر میشن؟
ب) چرا منهای در جایی که ظاهر می شوند ظاهر میشن؟
از نقطه نظر ریاضی، نمی توان یک ماتریس روتیشن کاملاً مثبت ساخت. این را می توان به راحتی از این خاصیت استنباط کرد که ماتریس های روتیشن دارای سیمتری انحرافی هستند، یعنی$R=R^{-T}$. به این ترتیب، نمی توان یک ماتریس روتاری را بدون منهای یا صفرهایی که روی عناصر غیر قطری ظاهر میشن تعریف کرد. به عنوان مثال، نمی توان (عدد واقعی) θ (نماینده یک زاویه) را برای به دست آوردن ماتریس زیر تعریف کرد و آن را ماتریس روتاری میگیم
$R\neq\left[\begin{matrix}\cos{\theta} & \sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{matrix}\right]$
(این ماتریس دو بعدی است اما در مورد سه بعدی هم همینطوره
توضیح بهتر که هر سه اکسیس کوردینیت سیستم دکارتی به صورت ارتوگونال با یکدیگر، یعنی در 90 درجه تعریف شدن. اگر نگاشت یک جزء کوردینیت سیستم افقی از Y به X نیاز به روتیشن 90 درجه داشته باشه، نتیجه آن اینه که مپ یا نگاشت از X به Y (یعنی بیس متقاطع مورب در ماتریس روتیشن) به روتیشن 90- درجه نیاز دارد. تفاوت بین این دو 180 درجه است، یعنی تغییر علامت.
پس منهای باید در جایی ظاهربشن اما چرا آنها همانطور که هستند ظاهر میشن در یک کوردینیت سیستم دو بعدی X-Y که در آن X به سمت راست و Y به سمت بالا ست میتوانیم روتیشن θ را در خلاف جهت عقربههای ساعت (cc) یا در جهت عقربههای ساعت (c) تعریف کنیم که به ترتیب به هر یک از دو ماتریس روتاری زیر منجر میشود:
$R_{cc}=\left[\begin{matrix}\cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{matrix}\right]$
$R_{c}=\left[\begin{matrix}\cos{\theta} & \sin{\theta} \\ -\sin{\theta} & \cos{\theta} \end{matrix}\right]$
این فقط یک کنوانسیون که اکسیس را برای اشاره به سمت راست و بالا وروتیشن در خلاف جهت عقربههای ساعت تعریف میکنه
حالا بیایید به سمت سه بعدی برویم. ما دیگر نمی توانیم به سادگی از جهت عقربه های ساعت و خلاف جهت عقربه های ساعت و راست و بالا حرف بزنیم زیرا مجبور نیستیم تصویر را از جهت خاصی ببینیم برای رفع این مشکل جزئی، کنوانسیون خود را به گونهای دوباره میاریم میکنیم که در سه بعدی نیز قابل اجرا باشه
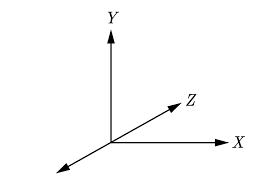
1)از سیستم های هماهنگ دکارتی راست دست استفاده می کنیم
سیستم هماهنگ راست دست
2) از روتاری راست دست استفاده می کنیم
روتیشن سمت راست
ا اگر مستقیماً به کوردینیت سیستم X-Y در امتداد Z نگاه کنیم همان سیستم را به دست می آوریم که در دو بعدی داشتیم (Y به سمت بالا، X اشاره به سمت راست). متوجه شدیم که Z به سمت شما اشاره می کند. به دلیل اشاره Z به سمت شما روتیشن خلاف جهت عقربه های ساعت خواهد بود و ما از ماتریس روتاری $R_{cc}$ استفاده می کنیم.
ما می توانیم همین کار را برای کوردینیت سیستم Y-Z انجام دهیم (Z به سمت بالا، Y به سمت راست) در امتداد X. اکنون X به سمت شما خواهد بود. باز هم از $R_{cc}$ استفاده می کنیم.
بعد، ما کوردینیت سیستم Z-X را داریم (X به سمت بالا، Z به سمت راست) در امتداد Y. دقیقاً همان را پیدا می کنیم یعنی Y به سمت شما اشاره میکنه. با این حال، Z-X در ماتریس روتیشن واضح به نظر نمیرسه زیرا ماتریس (مسطح) ما به جای دایره بودن، عرض و ارتفاع محدودی داره
اگر ماتریس روتیشن خود را از چپ به راستبخونید آنچه ظاهرمیشه به جای کوردینیت سیستم Z-X، همچنین در امتداد Y، کوردینیت سیستم X-Z است، اما اکنون میبینیم که Y اکنون به سمت شما نشانه میره. این باعث تغییر جهت روتیشن میشه. از اینجهت می بینید که Rc به جای $R_{cc}$ظاهر می شود.
تجزیه و تحلیل X-Y، Y-Z و Z-X منطقی تر از X-Y، Y-Z و X-Z است. سعی کنید ماتریس روتیشن خود را به صورت چرخهایتر بخونید نه از چپ به راست، اگر منطقیه سعی کنید X، Y و Z را موجودیتهای مستقلی در نظر بگیرید، نه اینکه Y بزرگتر از X و Z باشد. بزرگتر از Y و بنابراین بزرگتر از X.
قرارداد این ماتریسهای روتاری از همان جهت مثبت روتیشن پیروی میکند که حاصل ضرب در یک کوردینیت سیستم راست دست هست.
بنابراین یک روتیشن 90 درجه حول اکسیس x،اکسیس y را به اکسیس z مثبت واکسیس z را به اکسیس منفی y ترسیم می کند. یک روتیشن 90 درجه حول اکسیس y، اکسیس z را به اکسیس x مثبت و اکسیس x را بهاکسیس z منفی ترسیم میکنه. یک روتیشن 90 درجه حول اکسیس z، اکسیسx را به اکسیس y مثبت و اکسیس y را به اکسیس x منفی ترسیم می کند.
شما فرض کردید که به صورت ورتیکال ریورس نیستید و می پرسید چرا ورتیکال ریورس نیستید.
چرا تصاویر آینه ای به صورت افقی چرخانده میشن اما ورتیکال نیستند؟چرابه نظر میرسه که آینه ها L و R را می چرخانند؟ بدن شما یک صفحه آینه ای در امتداد اکسیس Z داره. هنگامی که حول اکسیسZ خود می چرخید تقریباً به همان شکلی به نظر می رسید که گویی خود را در آینه می بینید. تفاوتها با دستان شما که دستی را تغییر دادهاند
توجه داشته باشید، اگر حول اکسیسY خود بچرخانید و با دست ایستاده باشید
بنابراین آینهها نیز نمیتوانند آن را به طرفین برگردانند در عوض یک عمل سیمتری به نام آینه را پیش میکشه. وقتی 180 درجه بچرخین در حال انجام یک عملیات سیمتری دیگر به نام روتیشن هستید به عنوان روتیشن دو برابری نیز شناخته میگن هیچ چیز ذاتا درست تر از روتیشن در مقابلسیمتری آینه وجود نداره
چرا تصویر روی یک آینه مسطح به صورت لترال ریورس است؟
چرا در آینه صفحه لترال اینورژن وجود دارد؟ لترال اینورژن این دلیله که در یک آینه مسطح تصویر به همان اندازه که جسم در مقابل آن قرار دارد پشت آینه است و جلوی تصویر و جلوی جسم رو به روی هم هستند.آینه ها از چپ به راست ریورس نمی شوند، از جلو به عقب بر می گردند. این را در نظر بگیریدوقتی در آینه به خود نگاه می کنیدبه نظر میرسه کهه رفلکشن شما شخص دیگری است که دقیقاً شبیه شماست که پشت یک تکه شیشه ایستادین در همان فاصله ای که از شیشه دارید و رو به روی شماست. نکته مهم اینجاست - 180 درجه حول ورتیکال اکسیس چرخید تا رو به شما باشد. حالا دست چپ او باید مقابل دست راست شما باشد و بالعکس. در واقع این فرض اشتباه است. بازتاب شما روتیشن 180 درجه ای انجام نداد. از جلو به عقب و بدون هیچ روتاری برعکس بود. مغز شما روتیشن 180 درجه ای را که فرض می کنید باید اتفاق افتاده باشد را از نظر مشاهده شده از جلو به عقب کم می کند و چه چیزی به دست می آورید؟ یک برگشت ظاهری از چپ به راست!اگر در درک جهت همه چیز مشکل دارید در اینجا یک توضیح دقیق بدم: آینه تخت دایره ای در صفحه z=0 (افقی)، $x^2+y^2\le1$ است. آینه کروی نیمکره ای است که با z>0، $x^2+y^2+z^2=1$ توصیف میشه. شما در داخل ایستاده ایدخوب دست شما در نقطه ای نزدیک به اکسیس قرار داره برای مثال، (0.01، 0، 0.2). کاری که آینه ها انجام میدن اینکه برای یک جسم در یک نقطه (x,y,z)، آینه تخت تصویری را در (x,y,-z) ایجاد می کند (این تصویر دارای عقربه مخالفه زیرا یک کوردینیت سیستم برگردانده شده. سپس آینه کروی آن تصویر را در (x,y,−z) می گیرد و تصویر دیگری را در (−x,−y,z) ایجاد میکنه این تصویر همان دست بودن شی اصلی را دارد. همچنین سمت راست به بالا است زیراکوردینیت z برگردانده نشده است. تصویر دست راست شما در (0.01، 0، 0.2) به عنوان یک دست راست دیگر در (-0.01، 0، 0.2) ظاهر میشه که در جهت مناسب برای دست دادن شما قرار دارد.سردرگمی کونوانسیون علامت ماتریس روتیشن.

در ماتریس روتیشن، چرا روتیشن اول و سوم را در خلاف جهت روتیشن دوم می چرخانیم، این کمی گمراه کننده هست
در این تصویر می توان توجه داشت که برای روتیشن x و Z عناصر غیر صفر یکسان هستند. اما برای Y روتیشن علامت (تتا) تغییر کرد.


من فکر می کنم مسئله اصلی این است که شما سعی می کنید ماتریس های روتیشن خود را از چپ به راست بخونید. تغییرات علامت تصادفی به نظر میرسه اما در واقع به روشی معمولی روتیشن میکنه.
بیایید با این سوال شروع کنیم:
الف) اصلاً چرا منفی ها ظاهر میشن؟
ب) چرا منهای در جایی که ظاهر می شوند ظاهر میشن؟
از نقطه نظر ریاضی، نمی توان یک ماتریس روتیشن کاملاً مثبت ساخت. این را می توان به راحتی از این خاصیت استنباط کرد که ماتریس های روتیشن دارای سیمتری انحرافی هستند، یعنی$R=R^{-T}$. به این ترتیب، نمی توان یک ماتریس روتاری را بدون منهای یا صفرهایی که روی عناصر غیر قطری ظاهر میشن تعریف کرد. به عنوان مثال، نمی توان (عدد واقعی) θ (نماینده یک زاویه) را برای به دست آوردن ماتریس زیر تعریف کرد و آن را ماتریس روتاری میگیم
$R\neq\left[\begin{matrix}\cos{\theta} & \sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{matrix}\right]$
(این ماتریس دو بعدی است اما در مورد سه بعدی هم همینطوره
توضیح بهتر که هر سه اکسیس کوردینیت سیستم دکارتی به صورت ارتوگونال با یکدیگر، یعنی در 90 درجه تعریف شدن. اگر نگاشت یک جزء کوردینیت سیستم افقی از Y به X نیاز به روتیشن 90 درجه داشته باشه، نتیجه آن اینه که مپ یا نگاشت از X به Y (یعنی بیس متقاطع مورب در ماتریس روتیشن) به روتیشن 90- درجه نیاز دارد. تفاوت بین این دو 180 درجه است، یعنی تغییر علامت.
پس منهای باید در جایی ظاهربشن اما چرا آنها همانطور که هستند ظاهر میشن در یک کوردینیت سیستم دو بعدی X-Y که در آن X به سمت راست و Y به سمت بالا ست میتوانیم روتیشن θ را در خلاف جهت عقربههای ساعت (cc) یا در جهت عقربههای ساعت (c) تعریف کنیم که به ترتیب به هر یک از دو ماتریس روتاری زیر منجر میشود:
$R_{cc}=\left[\begin{matrix}\cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{matrix}\right]$
$R_{c}=\left[\begin{matrix}\cos{\theta} & \sin{\theta} \\ -\sin{\theta} & \cos{\theta} \end{matrix}\right]$
این فقط یک کنوانسیون که اکسیس را برای اشاره به سمت راست و بالا وروتیشن در خلاف جهت عقربههای ساعت تعریف میکنه
حالا بیایید به سمت سه بعدی برویم. ما دیگر نمی توانیم به سادگی از جهت عقربه های ساعت و خلاف جهت عقربه های ساعت و راست و بالا حرف بزنیم زیرا مجبور نیستیم تصویر را از جهت خاصی ببینیم برای رفع این مشکل جزئی، کنوانسیون خود را به گونهای دوباره میاریم میکنیم که در سه بعدی نیز قابل اجرا باشه
1)از سیستم های هماهنگ دکارتی راست دست استفاده می کنیم
سیستم هماهنگ راست دست
2) از روتاری راست دست استفاده می کنیم
روتیشن سمت راست
ا اگر مستقیماً به کوردینیت سیستم X-Y در امتداد Z نگاه کنیم همان سیستم را به دست می آوریم که در دو بعدی داشتیم (Y به سمت بالا، X اشاره به سمت راست). متوجه شدیم که Z به سمت شما اشاره می کند. به دلیل اشاره Z به سمت شما روتیشن خلاف جهت عقربه های ساعت خواهد بود و ما از ماتریس روتاری $R_{cc}$ استفاده می کنیم.
ما می توانیم همین کار را برای کوردینیت سیستم Y-Z انجام دهیم (Z به سمت بالا، Y به سمت راست) در امتداد X. اکنون X به سمت شما خواهد بود. باز هم از $R_{cc}$ استفاده می کنیم.
بعد، ما کوردینیت سیستم Z-X را داریم (X به سمت بالا، Z به سمت راست) در امتداد Y. دقیقاً همان را پیدا می کنیم یعنی Y به سمت شما اشاره میکنه. با این حال، Z-X در ماتریس روتیشن واضح به نظر نمیرسه زیرا ماتریس (مسطح) ما به جای دایره بودن، عرض و ارتفاع محدودی داره
اگر ماتریس روتیشن خود را از چپ به راستبخونید آنچه ظاهرمیشه به جای کوردینیت سیستم Z-X، همچنین در امتداد Y، کوردینیت سیستم X-Z است، اما اکنون میبینیم که Y اکنون به سمت شما نشانه میره. این باعث تغییر جهت روتیشن میشه. از اینجهت می بینید که Rc به جای $R_{cc}$ظاهر می شود.
تجزیه و تحلیل X-Y، Y-Z و Z-X منطقی تر از X-Y، Y-Z و X-Z است. سعی کنید ماتریس روتیشن خود را به صورت چرخهایتر بخونید نه از چپ به راست، اگر منطقیه سعی کنید X، Y و Z را موجودیتهای مستقلی در نظر بگیرید، نه اینکه Y بزرگتر از X و Z باشد. بزرگتر از Y و بنابراین بزرگتر از X.
قرارداد این ماتریسهای روتاری از همان جهت مثبت روتیشن پیروی میکند که حاصل ضرب در یک کوردینیت سیستم راست دست هست.
بنابراین یک روتیشن 90 درجه حول اکسیس x،اکسیس y را به اکسیس z مثبت واکسیس z را به اکسیس منفی y ترسیم می کند. یک روتیشن 90 درجه حول اکسیس y، اکسیس z را به اکسیس x مثبت و اکسیس x را بهاکسیس z منفی ترسیم میکنه. یک روتیشن 90 درجه حول اکسیس z، اکسیسx را به اکسیس y مثبت و اکسیس y را به اکسیس x منفی ترسیم می کند.


