یافتن اختلاف فشار
یافتن اختلاف فشار
ابعاد یک مکعب مستطیل 10 و 4و5 است این مکعب را یکبار از بزرگترین و یکبار از کوچک ترین سطح روی زمین قرار میدهیم اختلاف فشار ناشی چقدر است؟
- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3261-
سپاس: 5494
- جنسیت:
تماس:
Re: یافتن اختلاف فشار
جامدی که روی یک سطح افقی قرار داره نیروی تماسی معمولی برابر با وزن آن اعمال میکنه. فشار جامد بر روی سطح به سطح تماس بستگی دارد. ب) ناحیه تماس بین دو سطح. هر چه این نیرو بیشتر باشد یا منطقه کوچکتر باشد فشار بیشتر است.ببین $\vec{F}=p\vec{A}$بگوییم فشار به سمت فلان یا فلان جهت هدایت میشه. فشار، به عنوان یک اسکالر، جهتی نداره نیرویی که رابطه قبلی به کمیت می دهد جهت دارد اما فشار ندارد. اگر جهت عنصر سطح را تغییر دهیم، جهت نیروی نرمال بر این اساس تغییر می کند، اما فشار ثابت می ماند.
باید توضیح دهم که این نیروی ناشی از فشار را محاسبه می کند، بنابراین با توجه به بردار مساحت، نیروی عمود بر منطقه را به شما می دهد. این معادله تعیین کننده است و تنها معادله ای است که نشان می دهد فشار واقعا چه می کند، بنابراین همیشه درست است، اما باید به عنوان فرمولی برای محاسبه نیروی ناشی از فشار درک شود.راه درک فشار بر حسب تانسور تنش است و فشار برابر با اثر تانسور تنش است.
فشار یک کره به زمین
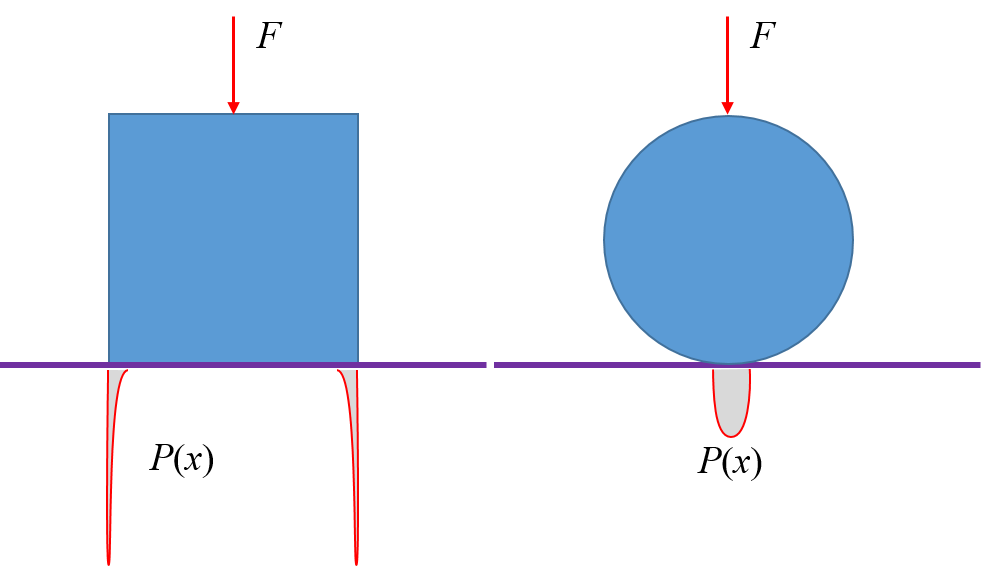
بنابراین همه ما می دانیم که فشار نیروی وارد شده به یک منطقه به این صورت تعریف می شود:
$P:=\frac{F}{A}$
جایی که F مقدار مولفه نیروی اعمال شده به صورت متعامد بر ناحیه A است
اکنون این رابطه برای محاسبه فشار وزن یک مکعب شبیه به یک ناحیه روی زمین مناسب است زیرا مکعب (اگر پایدار باشد) لزوماً در همه جهتهای ممکن سطح تماسی بزرگتر از صفر دارد.
اما اکنون یک کره را در نظر بگیرید که در ناحیه ای روی زمین ثابت است. ناگهان سطح تماس به یک نقطه کوچک میشه که به این معنی است که مقدارسطح تماس صفر است. آیا این بدان معناست که فشار کره توسط جرم آن بر روی زمین بی نهایت است
وضعیتی که من توصیف کردم به خوبی مطالعه شده است: توزیع تنش به عنوان استرس هرتزی شناخته می شود.
از آنجا که بستر (سطحی که کره روی آن قرار دارد) و خود کره هر دو دارای مدول الاستیک محدود هستند، سطوح تغییر شکل میدهند و ناحیه تماس واقعی دایرهای با اندازه محدود خواهد بود. توزیع تنش (به عنوان تابعی از شعاع) از یک قانون درجه دوم (به عنوان تابعی از فاصله از مرکز لکه تماس) پیروی می کند.
حرفهای من چند نتیجه کلیدی. ابتدا، شعاع a ناحیه تماس برای یک کره (شعاع R، مدول الاستیک E1، نسبت پواسون $\nu_1$) در صفحه ای با مدول الاستیک E2 و نسبت پواسون $\nu_2$ در صورت تحت تأثیر نیروی F (که ممکن است فقط وزن آن باشد. کره) توسط
$a = \sqrt{\frac34 FR\left(\frac{1-\nu_1^2}{E_1}+\frac{1-\nu_2^2}{E_2}{}\right)}$
و حداکثر فشار است
$P_0 = \frac{3F}{2\pi a^2}$
سپس توزیع فشار با فاصله شعاعی با استفاده از
$P(r) = P_0 \left(1-\frac{r^2}{a^2}\right)$
تئوری پشت این نظریه، نظریه تماس هرتزی هست . استدلال این است که مواد هرگز کاملاً صلب نیستند و با توجه به فشار اعمال شده بر سطح خود تغییر شکل می دهند. این تغییر شکل دو طرف یک تماس را مجبور می کند که هیچ همپوشانی نداشته باشند.ببین تنش تماسی هرتزی به تنش های موضعی میگن که با برخورد دو سطح منحنی ایجادمیشه و تحت بارهای تحمیلی کمی تغییر شکل میده این مقدار تغییر شکل به مدول الاستیسیته ماده در تماس بستگی داره
به محض اعمال بار بر روی تماس، تماس با تغییر شکل (فشرده شدن) بیشتر مواد پخش میشه. ناحیه تماس A با بار F تغییر می کند. برای یک کره، سطح با تئوری پشت این نظریه، نظریه تماس هرتزی نامیده می شود. استدلال این است که مواد هرگز کاملاً صلب نیستند و با توجه به فشار اعمال شده بر سطح خود تغییر شکل می دهند. این تغییر شکل دو طرف یک تماس را مجبور می کند که هیچ همپوشانی نداشته باشند.
به محض اعمال بار بر روی تماس، تماس با تغییر شکل (فشرده شدن) بیشتر مواد پخش می شود. ناحیه تماس A با بار F تغییر می کند. برای یک کره، سطح با $A \propto F^\frac{2}{3}$ و فشار اوج با $P_{max} \propto F^\frac{1}{3}$ تغییر می کند.
برای مکعب وضعیت در واقع پیچیده تر است، اما در اصل تماس به سرعت از مرکز پخش می شود و وقتی به لبه ها می رسد از اتاق خارج می شود. در کنسانتره ها فشار وجود دارد، همانطور که در تئوری اوج فشار روی لبه تیز بی نهایت است. در زندگی واقعی، تغییر شکلهای موضعی فشار اوج را از بینهایت پایین میارن، اما هنوز در مقایسه با حالت کروی، مقدار بسیار بالایی است.نیروی نرمال تماسی متناسب با "مدول یانگ جهت دار" است:
$F_{_N} \propto \frac {E}{1-\nu ^{2}} ,$
اساساً، به این معنیه که ماده می تواند با نیروی نرمال قوی پاسخ دهد، یا اگر دارای سفتی بالا یا نسبت پواسون بالا باشه به این معنی که ماده می تواند تغییر شکل را در جهات عمود بر نیروی خرد کننده اعمال شده جمع کند و سپس آن را به عقب رها کنه این فرآیند به بهترین وجه از تصویری که گذاشتم معلومه
باید توضیح دهم که این نیروی ناشی از فشار را محاسبه می کند، بنابراین با توجه به بردار مساحت، نیروی عمود بر منطقه را به شما می دهد. این معادله تعیین کننده است و تنها معادله ای است که نشان می دهد فشار واقعا چه می کند، بنابراین همیشه درست است، اما باید به عنوان فرمولی برای محاسبه نیروی ناشی از فشار درک شود.راه درک فشار بر حسب تانسور تنش است و فشار برابر با اثر تانسور تنش است.
فشار یک کره به زمین

بنابراین همه ما می دانیم که فشار نیروی وارد شده به یک منطقه به این صورت تعریف می شود:
$P:=\frac{F}{A}$
جایی که F مقدار مولفه نیروی اعمال شده به صورت متعامد بر ناحیه A است
اکنون این رابطه برای محاسبه فشار وزن یک مکعب شبیه به یک ناحیه روی زمین مناسب است زیرا مکعب (اگر پایدار باشد) لزوماً در همه جهتهای ممکن سطح تماسی بزرگتر از صفر دارد.
اما اکنون یک کره را در نظر بگیرید که در ناحیه ای روی زمین ثابت است. ناگهان سطح تماس به یک نقطه کوچک میشه که به این معنی است که مقدارسطح تماس صفر است. آیا این بدان معناست که فشار کره توسط جرم آن بر روی زمین بی نهایت است
وضعیتی که من توصیف کردم به خوبی مطالعه شده است: توزیع تنش به عنوان استرس هرتزی شناخته می شود.
از آنجا که بستر (سطحی که کره روی آن قرار دارد) و خود کره هر دو دارای مدول الاستیک محدود هستند، سطوح تغییر شکل میدهند و ناحیه تماس واقعی دایرهای با اندازه محدود خواهد بود. توزیع تنش (به عنوان تابعی از شعاع) از یک قانون درجه دوم (به عنوان تابعی از فاصله از مرکز لکه تماس) پیروی می کند.
حرفهای من چند نتیجه کلیدی. ابتدا، شعاع a ناحیه تماس برای یک کره (شعاع R، مدول الاستیک E1، نسبت پواسون $\nu_1$) در صفحه ای با مدول الاستیک E2 و نسبت پواسون $\nu_2$ در صورت تحت تأثیر نیروی F (که ممکن است فقط وزن آن باشد. کره) توسط
$a = \sqrt{\frac34 FR\left(\frac{1-\nu_1^2}{E_1}+\frac{1-\nu_2^2}{E_2}{}\right)}$
و حداکثر فشار است
$P_0 = \frac{3F}{2\pi a^2}$
سپس توزیع فشار با فاصله شعاعی با استفاده از
$P(r) = P_0 \left(1-\frac{r^2}{a^2}\right)$
تئوری پشت این نظریه، نظریه تماس هرتزی هست . استدلال این است که مواد هرگز کاملاً صلب نیستند و با توجه به فشار اعمال شده بر سطح خود تغییر شکل می دهند. این تغییر شکل دو طرف یک تماس را مجبور می کند که هیچ همپوشانی نداشته باشند.ببین تنش تماسی هرتزی به تنش های موضعی میگن که با برخورد دو سطح منحنی ایجادمیشه و تحت بارهای تحمیلی کمی تغییر شکل میده این مقدار تغییر شکل به مدول الاستیسیته ماده در تماس بستگی داره
به محض اعمال بار بر روی تماس، تماس با تغییر شکل (فشرده شدن) بیشتر مواد پخش میشه. ناحیه تماس A با بار F تغییر می کند. برای یک کره، سطح با تئوری پشت این نظریه، نظریه تماس هرتزی نامیده می شود. استدلال این است که مواد هرگز کاملاً صلب نیستند و با توجه به فشار اعمال شده بر سطح خود تغییر شکل می دهند. این تغییر شکل دو طرف یک تماس را مجبور می کند که هیچ همپوشانی نداشته باشند.
به محض اعمال بار بر روی تماس، تماس با تغییر شکل (فشرده شدن) بیشتر مواد پخش می شود. ناحیه تماس A با بار F تغییر می کند. برای یک کره، سطح با $A \propto F^\frac{2}{3}$ و فشار اوج با $P_{max} \propto F^\frac{1}{3}$ تغییر می کند.
برای مکعب وضعیت در واقع پیچیده تر است، اما در اصل تماس به سرعت از مرکز پخش می شود و وقتی به لبه ها می رسد از اتاق خارج می شود. در کنسانتره ها فشار وجود دارد، همانطور که در تئوری اوج فشار روی لبه تیز بی نهایت است. در زندگی واقعی، تغییر شکلهای موضعی فشار اوج را از بینهایت پایین میارن، اما هنوز در مقایسه با حالت کروی، مقدار بسیار بالایی است.نیروی نرمال تماسی متناسب با "مدول یانگ جهت دار" است:
$F_{_N} \propto \frac {E}{1-\nu ^{2}} ,$
اساساً، به این معنیه که ماده می تواند با نیروی نرمال قوی پاسخ دهد، یا اگر دارای سفتی بالا یا نسبت پواسون بالا باشه به این معنی که ماده می تواند تغییر شکل را در جهات عمود بر نیروی خرد کننده اعمال شده جمع کند و سپس آن را به عقب رها کنه این فرآیند به بهترین وجه از تصویری که گذاشتم معلومه



