پیدا کردن شعای دایره با داشتن تنها یک کمان
پیدا کردن شعای دایره با داشتن تنها یک کمان
سلام آیا میتوان با داشتن تنها یک کمان ( بدون داشتن زاویه و هرگونه پارامتر دیگری) شعاع دایره‌ای را که آن کمان میتواند بر روی آن باشد را محاسبه کرد؟
-
rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سه‌شنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3287-
سپاس: 5494
- جنسیت:
تماس:
Re: پیدا کردن شعای دایره با داشتن تنها یک کمان
شعاع دایره را با توجه به طول و ارتفاع وتر یک قطعه محاسبه کنیدمن یک بخش (دایره ای) با ارتفاع مشخص و طول وتر مشخص دارم. آیا می توان شعاع دایره را تعیین کرد؟می توانیم قضیه آکوردهای متقاطع را اعمال کنیم.طول آکورد شما طول UV است و ارتفاع قطعه به طول PX است.قضیه آکوردهای متقاطع به ما می گوید که$XP \times XQ = XU \times XV$
.اجازه دهید$\ell = UV$ و $h=XP$. نتیجه این است که $UX = XV = \tfrac{1}{2}\ell$
. سپس ICT این را به ما می گوید$\tfrac{1}{2}\ell \times \tfrac{1}{2}\ell = h \times XQ \, ,$
یعنی $XQ = \tfrac{1}{4h}\ell^2$. قطر $PQ=PX+XQ$ و$PX + XQ = h + \frac{\ell^2}{4h}=\frac{4h^2+\ell^2}{4h}$سپس شعاع نصف این است، یعنی.
$CQ = \frac{4h^2+\ell^2}{8h} \, .$تصویر ببین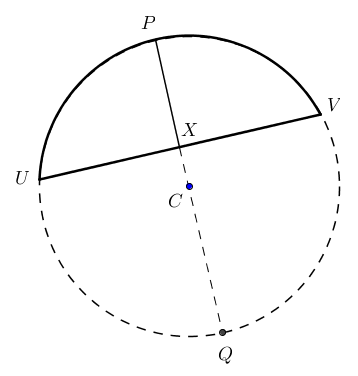
پس طول کمان می‌شود:
${\displaystyle L={\frac {\alpha \pi r}{180}}.\,\!}$
سطح کمان
سطح میان یک کمان و مرکز دایره عبارت است از:
${\displaystyle A={\frac {1}{2}}r^{2}\theta .}$
نسبت سطح:A به سطح کل دایره برابر است با نسبت زاویهٔ
$\theta $ به زاویهٔ کل دایره:${\displaystyle {\frac {A}{\pi r^{2}}}={\frac {\theta }{2\pi }}.}$
$\pi $ از دو طرف تساوی ساده می‌شود آنگاه:${\displaystyle {\frac {A}{r^{2}}}={\frac {\theta }{2}}.}$
دو طرف تساوی را در ${\displaystyle \ r^{2}} $ضرب می‌کنیم:
${\displaystyle A={\frac {1}{2}}r^{2}\theta .}$اگر زاویه بجای رادیان به درجه داده شده بود، سطح کمان آن می‌شد:
${\displaystyle A={\frac {\alpha }{360}}\pi r^{2}.}$مساحت قطاع منحنی کمانبرای آگاهی بیشتر مقالهٔ قطاع دایره را نگاه کنید.
سطح میان کمان دایره و پاره خط رسانندهٔ دو سر کمان به یکدیگر عبارت است از:
${\displaystyle {\frac {1}{2}}r^{2}(\theta -\sin {\theta }).}$
برای بدست آوردن سطح قطاع دایره باید مساحت مثلث تولید شده در مرکز دایره (با ضلع‌های شعاع دایره) را از مساحت کمان که در بالا توضیح داده شد کم کنیم.
شعاع کمان با استفاده از نظریهٔ سکانت - تانژانت یا توان یک نقطه میتوان شعاع
r یک دایره را با استفاده از درازای H و پهنای W یکی از کمان‌های آن به صورت زیر بدست آورد:
${\displaystyle r={\frac {W^{2}}{8H}}+{\frac {H}{2}}}$
خمیدگی منحنی منحنی یا خم مسطح $$ C $$ را میتوان به صورت پارامتری با بردار شعاعی $$ \mathbf{r}\left( t \right) $$ تعریف کرد.
وقتی نقطه $$ M$$ در طول منحنی $$ C $$ حرکت می‌کند، جهت خط مماس یا شیب تغییر خواهد کرد
انحنا یا خمیدگی منحنی را میتوان به عنوان نسبت زاویه چرخش $$\Delta \varphi$$ خط مماس نسبت به طول $$\Delta s = M{M_1}$$ کمان یا قوس پیموده شده تعریف کرد. این نسبت $$\large\frac{{\Delta \varphi }}{{\Delta s}}\normalsize $$ خمیدگی میانگین یا متوسط منحنی نامیده می‌شود. وقتی نقطه $$ M _ 1 $$ به نقطه $$ M $$ نزدیک می‌شود، خمیدگی منحنی در نقطه $$ M $$ به دست می‌آید:$$ \large k = \lim \limits _ { \Delta s \to 0 } \frac { { \Delta \varphi } } { { \Delta s } } = \frac { { d \varphi } } { { d s } } . $$
واضح است که خمیدگی $$ k $$ در حالت کلی، بسته به جهت چرخش مماس، مثبت یا منفی است.اگر یک منحنی با بردار شعاعی $$\mathbf{r}\left( t \right) $$ تعریف شده باشد، خمیدگی به صورت زیر خواهد بود:$$ \large k = \frac { { \mathbf { r’ } \times \mathbf { r ^ { \prime \prime } } } } { { { { \left | { \mathbf { r’ } } \right | } ^ 3 } } } \, $$
که $$\mathbf{r}’$$ و $$\mathbf{r}^{\prime\prime} $$ مشتق‌های اول و دوم بردار شعاعی هستند.اگر مختصات یک منحنی با تابع صریح $$ y = f ( x ) $$ داده شده باشد، خمیدگی با فرمول زیر محاسبه می‌شود:$$ \large k = \frac { { y ^ { \prime \prime } } } { { { { \left [ { 1 + { { \left ( { y’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . $$
در حالتی که منحنی در مختصات قطبی به فرم $$\rho = \rho \left( \varphi \right) $$ داده شده باشد، خمیدگی $$ k $$ با عبارت زیر تعریف می‌شود:
$$ \large { k \left ( \varphi \right ) } = { \frac { { { \rho ^ 2 } + 2 { { \left ( { \rho’ } \right ) } ^ 2 } – \rho \rho ^ { \prime \prime } } } { { { { \left [ { { \rho ^ 2 } + { { \left ( { \rho’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . } $$خمیدگی منحنی اغلب به عنوان قدر مطلق خمیدگی در نظر گرفته می‌شود، بدون اینکه جهت چرخش آن در نظر گرفته شود. در این حالت، فرمول‌های بالا معتبر هستند، اما قدر مطلق در صورت ظاهر می‌شود. برای مثال، وقتی مختصات $$ x ( t) $$ و $$ y ( t) $$ یک منحنی به صورت پارامتری داده شده باشند، فرمول خمیدگی به صورت زیر خواهد بود:
$$ \large k = \frac { { \left | { x’ y ^ { \prime \prime } – y’ x ^ { \prime \prime } } \right | } } { { { { \left [ { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . $$وارون خمیدگی، شعاع خمیدگی نامیده می‌شود:$$ \large R = \frac { 1 } { { \left | k \right | } } . $$
دایره‌ای به این شعاع و مرکز، روی خط قائم داخلی واقع شده است که نزدیک‌ترین تقریب منحنی مسطح در نقطه داد شده است
چنین دایره‌ای، «دایره بوسان» (Osculating Circle) نامیده می‌شود.
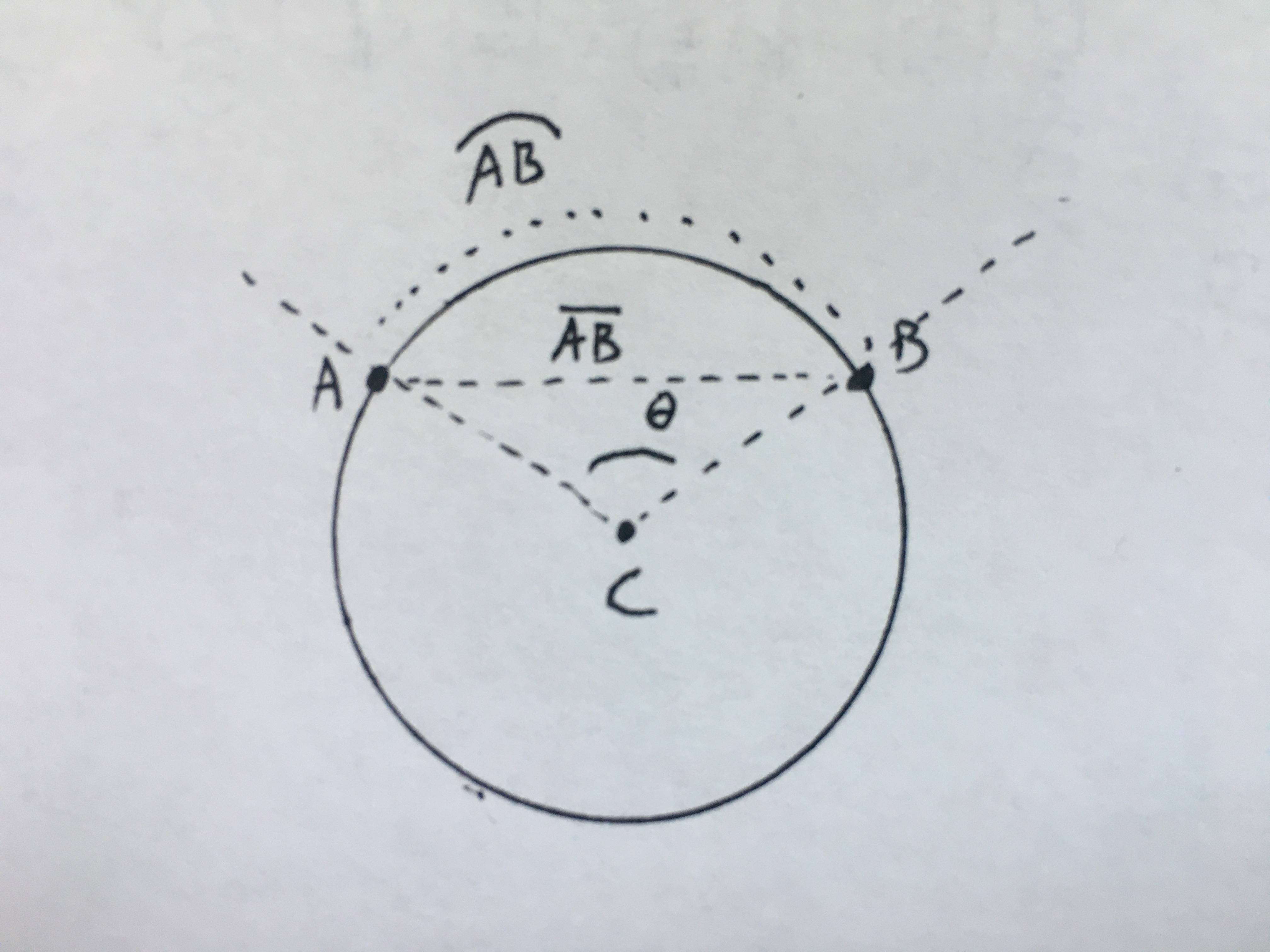
من نکاتی را که در تصویر بالا نشان داده شده است دریافت کردم: A و B، که شناخته شده اند - بنابراین فاصله بین آنها (با برچسب $\overline{\rm AB}$
). همچنین طول قوس،$\overset{\mmlToken{mo}{⏜}}{AB\,}$شناخته شده/داده شده است
. من سعی می کنم$\overline{\rm AC}$یا$\overline{\rm BC}$ را پیدا کنم
) و/یا θ. (C ناشناخته است.)$\overset{\mmlToken{mo}{⏜}}{AB\,} = \theta R,\space \text{thus}\space R = \frac{\overset{\mmlToken{mo}{⏜}}{AB\,}}{\theta}$
$2R \sin (\frac{\theta}{2}) = \overline{\rm AB}, \space \text{so}\space R = \frac{\overline{\rm AB}}{2\sin (\frac{\theta}{2})}$با استفاده از این موارد می توانیم پیدا کنیم:$\frac{\overset{\mmlToken{mo}{⏜}}{AB\,}}{\theta} = \frac{\overline{\rm AB}}{2\sin (\frac{\theta}{2})}$با مقداری بازآرایی،$\sin (\frac{\theta}{2}) = \frac{\overline{\rm AB}}{\overset{\mmlToken{mo}{⏜}}{AB\,}}\frac{\theta}{2}$از اینجا می‌توانیم مقداری تغییر انتساب متغیر را انجام دهیم: من می‌گویم$t = \frac{\theta}{2}$و$k = \frac{\overline{\rm AB}}{\overset{\mmlToken{mo}{⏜}}{AB\,}}$این به ما می دهد$\sin (t) = kt$من راهی برای k نمی بینم تا 1 باشد (و k=1
فقط اگر شعاع بی نهایت و تتا 0 باشد)، اما من فرض میکنم تتا میتواند اساساً هر زاویه‌ای باشد - من آن را برای مثبت حل میکنم، و برای مورد استفاده من انتظار دارم همیشه در $0-\pi$ باشد.
محدوده، اما حدس می‌زنم که لازم نباشد.
من از جنبه هندسی چیزها نسبتاً مطمئن هستم. که برای من منطقی است سعی کردم کاری مثل $\frac{\sin (t)}{t} = k$ انجام دهم
، اما من هنوز نمی دانم چگونه می توانم این را از نظر محاسباتی تقریب کنم - روش نیوتن $t_{k+1} = t_k - \dfrac{\sin t_k - K t_k} {\cos t_k - K}$بنابراین من طول وتر را می دانم (C) و طول قوس (Aاما مشکل داشتن R وجود داردبنابراین می توانم فرمول را کمی تغییر دهم تا برابر با صفر شود و آن را وصل کنم$0=\frac{C}{2\sin\left(\frac{360A}{4\pi R}\right)}-R$
انحنا و شعاع انحنا Curvature and radius of curvature
منحنی صفحه ای را در نظر بگیرید که با معادله y = f (x) تعریف شده است. فرض کنید که خط مماس به منحنی در نقطه M(x,y) کشیده شده است. مماس یک زاویه α با محور افقی تشکیل می دهد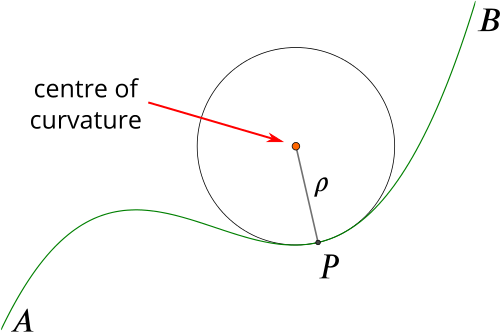
]با جابجایی Δs در طول کمان منحنی، نقطه M به سمت نقطه M1 حرکت خواهد کرد. در این صورت، موقعیت خط مماس نیز تغییر می‌کند؛ زاویه شیب خط مماس بر نقطه M1 و محور مثبت x، α+Δα خواهد بود. بنابراین، با حرکت نقطه به اندازه Δs، خط مماس به اندازه Δα می‌چرخد (فرض شده که وقتی جهت حرکت زاویه α پادساعتگرد باشد، افزایشی خواهد بود.)قدر مطلق نسبت $\frac{{\Delta \alpha }}{{\Delta s}}$ انحنا یا خمیدگی متوسط کمان MM1 نامیده می‌شود. با حد$\Delta s \to 0,$، انحنای منحنی در نقطه M به صورت زیر محاسبه می‌شود:$\large K = \lim \limits _ { \Delta s \to 0 } \left | { \frac { { \Delta \alpha } } { { \Delta s } } } \right | .$برای یک منحنی مسطح با معادله y=f(x)، انحنا در نقطه M(x,y) بر حسب مشتق‌های اول و دوم تابع$y = f\left( x \right),$ و با فرمول زیر بیان می‌شود:$K = \frac{{\left| {y^{\prime\prime}\left( x \right)} \right|}}{{{{\left[ {1 + {{\left( {y'\left( x \right)} \right)}^2}} \right]}^{\frac{3}{2}}}}}.$اگر منحنی به فرم پارامتری و با معادلات x=x(t) و y=y(t) تعریف شده باشد، آنگاه انحنا در نقطه M(x,y) با رابطه زیر تعیین می‌شود:$K = \frac{{\left| {x'y^{\prime\prime} - y'x^{\prime\prime}} \right|}}{{{{\left[ {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2}} \right]}^{\frac{3}{2}}}}}.$اگر یک منحنی با معادله قطبی داده شود، انحنا با فرمول محاسبه می شود$K = \frac{{\left| {{r^2} + 2{{\left( {r'} \right)}^2} - rr^{\prime\prime}} \right|}}{{{{\left[ {{r^2} + {{\left( {r'} \right)}^2}} \right]}^{\frac{3}{2}}}}}.$شعاع هم نسبست عکس با انحنا داره$\large R = \frac { 1 } { K } .$یعنی $R = \frac{{{{\left[ {1 + {{\left( {y'\left( x \right)} \right)}^2}} \right]}^{\frac{3}{2}}}}}{{\left| {y^{\prime\prime}\left( x \right)} \right|}}.$
بدیهی است که برای یافتن انحنای بیضی در نقاط و (شکل ) کافی است، زیرا به دلیل تقارن منحنی، انحنای دو راس مخالف بیضی یکسان خواهد بود.برای محاسبه انحنا، راحت است که از معادله متعارف بیضی به معادله به شکل پارامتریک عبور کنیم:$x = a\cos t,\;\;\;y = b\sin t,$پس من میام فرمول اجرا میکنم $x' = {x'_t} = \left( {a\cos t} \right)^\prime = - a\sin t,\;\;\;x^{\prime\prime} = x^{\prime\prime}_{tt} = \left( { - a\sin t} \right)^\prime = - a\cos t;$.و به طور سیمیلار برای y خوب بعد محاسبه من $K = \frac{{\left| {ab\,{{\sin }^2}t + ab\,{{\cos }^2}t} \right|}}{{{{\left( {{a^2}{{\sin }^2}t + {b^2}{{\cos }^2}t} \right)}^{\frac{3}{2}}}}} = \frac{{\left| {ab\left( {{{\sin }^2}t + {{\cos }^2}t} \right)} \right|}}{{{{\left( {{a^2}{{\sin }^2}t + {b^2}{{\cos }^2}t} \right)}^{\frac{3}{2}}}}} = \frac{{ab}}{{{{\left( {{a^2}{{\sin }^2}t + {b^2}{{\cos }^2}t} \right)}^{\frac{3}{2}}}}}.$و من دو مقدار برای t انتخاب میکنم$K\left( A \right) = K\left( {t = 0} \right) = \frac{{ab}}{{{{\left( {{a^2}{{\sin }^2}0 + {b^2}{{\cos }^2}0} \right)}^{\frac{3}{2}}}}} = \frac{{ab}}{{{{\left( {{b^2}} \right)}^{\frac{3}{2}}}}} = \frac{{ab}}{{{b^3}}} = \frac{a}{{{b^2}}};$و $K\left( B \right) = K\left( {t = \frac{\pi }{2}} \right) = \frac{{ab}}{{{{\left( {{a^2}{{\sin }^2}\frac{\pi }{2} + {b^2}{{\cos }^2}\frac{\pi }{2}} \right)}^{\frac{3}{2}}}}} = \frac{{ab}}{{{{\left( {{a^2}} \right)}^{\frac{3}{2}}}}} = \frac{{ab}}{{{a^3}}} = \frac{b}{{{a^2}}}.$انحنای ابربیضی را که با معادلات پارامتری تعریف شده است، بیابید$x\left( t \right) = a\, {\cos ^n}t,\; y\left( t \right) = b\,{\sin ^n}t,$ابربیضی ها منحنی های خوبی هستند که شکل آن ها بین دایره و مربع است. آنها کاربردهای زیادی در طراحی و مهندسی دارند.
شکل یک منحنی با انحنای آن مشخص می شود. در این مسئله، فرمول کلی انحنای یک ابربیضی با توان مثبت دلخواه را استخراج می کنیم.$K \text = \frac{{ab{2^{1 - n}}\left| {\left( {2 - n} \right){{\sin }^{n - 1}}2t} \right|}}{{{{n\left[ {{a^2}{{\cos }^{2n - 2}}t\,{{\sin }^2}t + {b^2}{{\sin }^{2n - 2}}t\,{{\cos }^2}t} \right]}^{\frac{3}{2}}}}}.$
خمیدگی در حقیقت معادل با میزان تغییر جهت یک تابع برداری یا همان تابع پارامتری نسبت به پارامتر وابسته است. روابط زیادی به منظور بدست آوردن خمیدگی توابع پارامتری وجود دارد. با این حال تعریف کلی خمیدگی به صورت زیر است.$\Large \kappa = \left | { \frac { { d \, \overrightarrow T } } { {d s } } } \right|$در رابطه فوق، s برابر با طول خم و T نشان دهنده بردار مماس به خم است. همان‌طور که در مطلب توابع برداری نیز بیان شد، به منظور بدست آوردن خمیدگی یک تابع، در ابتدا باید، آن را به صورت پارامتری بیان کرده، سپس قادر خواهیم بود تا خمیدگی آن را محاسبه کنیم.$\large \kappa = \frac{{\left\| {\overrightarrow T ^ {\prime} \left( t \right)} \right\|}}{{\left\| {\overrightarrow r ^ {\prime} \left( t \right)} \right\|}}\hspace{1.0in}\kappa = \frac{{\left\| {\overrightarrow r ^{ \prime } \left( t \right) \times \overrightarrow r ^{\prime\prime} \left( t \right)} \right\|}}{{{{\left\| {\overrightarrow r ^ {\prime} \left( t \right)} \right\|}^3}}}$اجازه دهید یک منحنی صفحه به صورت پارامتریک توسط بردار شعاع تعریف شود در حالی که یک نقطه در امتداد منحنی حرکت می کند، جهت مماس تغییر می کندانحنای منحنی را می توان به عنوان نسبت زاویه چرخش مماس به طول قوس پیموده شده این نسبت تعریف کرد.
انحنای متوسط منحنی نامیده می شود. هنگامی که نقطه به نقطه نزدیک می شود، انحنای منحنی را در نقطه به دست می آوریم$k = \lim\limits_{\Delta s \to 0} \frac{{\Delta \varphi }}{{\Delta s}} = \frac{{d\varphi }}{{ds}}.$واضح است که انحنا در حالت کلی بسته به جهت چرخش مماس می تواند مثبت یا منفی باشد.
اگر یک منحنی با بردار شعاع تعریف شود، انحنای آن توسط بردار مشخص می شود$k = \frac{{\mathbf{r'} \times \mathbf{r^{\prime\prime}}}}{{{{\left| {\mathbf{r'}} \right|}^3}}},$
اگر مختصات یک منحنی به صورت پارامتری به صورت و مشخص شود، فرمول محاسبه انحنا به شکل$k = \frac{{x'y^{\prime\prime} - y'x^{\prime\prime}}}{{{{\left[ {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2}} \right]}^{\frac{3}{2}}}}}.$در موردی که یک منحنی در مختصات قطبی به شکل داده می شود انحنای آن با عبارت تعریف می شود$k\left( \varphi \right) = \frac{{{\rho ^2} + 2{{\left( {\rho'} \right)}^2} - \rho \rho^{\prime\prime}}}{{{{\left[ {{\rho ^2} + {{\left( {\rho'} \right)}^2}} \right]}^{\frac{3}{2}}}}}.$hope I helped you understand the question. Roham Hesami,
.اجازه دهید$\ell = UV$ و $h=XP$. نتیجه این است که $UX = XV = \tfrac{1}{2}\ell$
. سپس ICT این را به ما می گوید$\tfrac{1}{2}\ell \times \tfrac{1}{2}\ell = h \times XQ \, ,$
یعنی $XQ = \tfrac{1}{4h}\ell^2$. قطر $PQ=PX+XQ$ و$PX + XQ = h + \frac{\ell^2}{4h}=\frac{4h^2+\ell^2}{4h}$سپس شعاع نصف این است، یعنی.
$CQ = \frac{4h^2+\ell^2}{8h} \, .$تصویر ببین
پس طول کمان می‌شود:
${\displaystyle L={\frac {\alpha \pi r}{180}}.\,\!}$
سطح کمان
سطح میان یک کمان و مرکز دایره عبارت است از:
${\displaystyle A={\frac {1}{2}}r^{2}\theta .}$
نسبت سطح:A به سطح کل دایره برابر است با نسبت زاویهٔ
$\theta $ به زاویهٔ کل دایره:${\displaystyle {\frac {A}{\pi r^{2}}}={\frac {\theta }{2\pi }}.}$
$\pi $ از دو طرف تساوی ساده می‌شود آنگاه:${\displaystyle {\frac {A}{r^{2}}}={\frac {\theta }{2}}.}$
دو طرف تساوی را در ${\displaystyle \ r^{2}} $ضرب می‌کنیم:
${\displaystyle A={\frac {1}{2}}r^{2}\theta .}$اگر زاویه بجای رادیان به درجه داده شده بود، سطح کمان آن می‌شد:
${\displaystyle A={\frac {\alpha }{360}}\pi r^{2}.}$مساحت قطاع منحنی کمانبرای آگاهی بیشتر مقالهٔ قطاع دایره را نگاه کنید.
سطح میان کمان دایره و پاره خط رسانندهٔ دو سر کمان به یکدیگر عبارت است از:
${\displaystyle {\frac {1}{2}}r^{2}(\theta -\sin {\theta }).}$
برای بدست آوردن سطح قطاع دایره باید مساحت مثلث تولید شده در مرکز دایره (با ضلع‌های شعاع دایره) را از مساحت کمان که در بالا توضیح داده شد کم کنیم.
شعاع کمان با استفاده از نظریهٔ سکانت - تانژانت یا توان یک نقطه میتوان شعاع
r یک دایره را با استفاده از درازای H و پهنای W یکی از کمان‌های آن به صورت زیر بدست آورد:
${\displaystyle r={\frac {W^{2}}{8H}}+{\frac {H}{2}}}$
خمیدگی منحنی منحنی یا خم مسطح $$ C $$ را میتوان به صورت پارامتری با بردار شعاعی $$ \mathbf{r}\left( t \right) $$ تعریف کرد.
وقتی نقطه $$ M$$ در طول منحنی $$ C $$ حرکت می‌کند، جهت خط مماس یا شیب تغییر خواهد کرد
انحنا یا خمیدگی منحنی را میتوان به عنوان نسبت زاویه چرخش $$\Delta \varphi$$ خط مماس نسبت به طول $$\Delta s = M{M_1}$$ کمان یا قوس پیموده شده تعریف کرد. این نسبت $$\large\frac{{\Delta \varphi }}{{\Delta s}}\normalsize $$ خمیدگی میانگین یا متوسط منحنی نامیده می‌شود. وقتی نقطه $$ M _ 1 $$ به نقطه $$ M $$ نزدیک می‌شود، خمیدگی منحنی در نقطه $$ M $$ به دست می‌آید:$$ \large k = \lim \limits _ { \Delta s \to 0 } \frac { { \Delta \varphi } } { { \Delta s } } = \frac { { d \varphi } } { { d s } } . $$
واضح است که خمیدگی $$ k $$ در حالت کلی، بسته به جهت چرخش مماس، مثبت یا منفی است.اگر یک منحنی با بردار شعاعی $$\mathbf{r}\left( t \right) $$ تعریف شده باشد، خمیدگی به صورت زیر خواهد بود:$$ \large k = \frac { { \mathbf { r’ } \times \mathbf { r ^ { \prime \prime } } } } { { { { \left | { \mathbf { r’ } } \right | } ^ 3 } } } \, $$
که $$\mathbf{r}’$$ و $$\mathbf{r}^{\prime\prime} $$ مشتق‌های اول و دوم بردار شعاعی هستند.اگر مختصات یک منحنی با تابع صریح $$ y = f ( x ) $$ داده شده باشد، خمیدگی با فرمول زیر محاسبه می‌شود:$$ \large k = \frac { { y ^ { \prime \prime } } } { { { { \left [ { 1 + { { \left ( { y’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . $$
در حالتی که منحنی در مختصات قطبی به فرم $$\rho = \rho \left( \varphi \right) $$ داده شده باشد، خمیدگی $$ k $$ با عبارت زیر تعریف می‌شود:
$$ \large { k \left ( \varphi \right ) } = { \frac { { { \rho ^ 2 } + 2 { { \left ( { \rho’ } \right ) } ^ 2 } – \rho \rho ^ { \prime \prime } } } { { { { \left [ { { \rho ^ 2 } + { { \left ( { \rho’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . } $$خمیدگی منحنی اغلب به عنوان قدر مطلق خمیدگی در نظر گرفته می‌شود، بدون اینکه جهت چرخش آن در نظر گرفته شود. در این حالت، فرمول‌های بالا معتبر هستند، اما قدر مطلق در صورت ظاهر می‌شود. برای مثال، وقتی مختصات $$ x ( t) $$ و $$ y ( t) $$ یک منحنی به صورت پارامتری داده شده باشند، فرمول خمیدگی به صورت زیر خواهد بود:
$$ \large k = \frac { { \left | { x’ y ^ { \prime \prime } – y’ x ^ { \prime \prime } } \right | } } { { { { \left [ { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . $$وارون خمیدگی، شعاع خمیدگی نامیده می‌شود:$$ \large R = \frac { 1 } { { \left | k \right | } } . $$
دایره‌ای به این شعاع و مرکز، روی خط قائم داخلی واقع شده است که نزدیک‌ترین تقریب منحنی مسطح در نقطه داد شده است
چنین دایره‌ای، «دایره بوسان» (Osculating Circle) نامیده می‌شود.
من نکاتی را که در تصویر بالا نشان داده شده است دریافت کردم: A و B، که شناخته شده اند - بنابراین فاصله بین آنها (با برچسب $\overline{\rm AB}$
). همچنین طول قوس،$\overset{\mmlToken{mo}{⏜}}{AB\,}$شناخته شده/داده شده است
. من سعی می کنم$\overline{\rm AC}$یا$\overline{\rm BC}$ را پیدا کنم
) و/یا θ. (C ناشناخته است.)$\overset{\mmlToken{mo}{⏜}}{AB\,} = \theta R,\space \text{thus}\space R = \frac{\overset{\mmlToken{mo}{⏜}}{AB\,}}{\theta}$
$2R \sin (\frac{\theta}{2}) = \overline{\rm AB}, \space \text{so}\space R = \frac{\overline{\rm AB}}{2\sin (\frac{\theta}{2})}$با استفاده از این موارد می توانیم پیدا کنیم:$\frac{\overset{\mmlToken{mo}{⏜}}{AB\,}}{\theta} = \frac{\overline{\rm AB}}{2\sin (\frac{\theta}{2})}$با مقداری بازآرایی،$\sin (\frac{\theta}{2}) = \frac{\overline{\rm AB}}{\overset{\mmlToken{mo}{⏜}}{AB\,}}\frac{\theta}{2}$از اینجا می‌توانیم مقداری تغییر انتساب متغیر را انجام دهیم: من می‌گویم$t = \frac{\theta}{2}$و$k = \frac{\overline{\rm AB}}{\overset{\mmlToken{mo}{⏜}}{AB\,}}$این به ما می دهد$\sin (t) = kt$من راهی برای k نمی بینم تا 1 باشد (و k=1
فقط اگر شعاع بی نهایت و تتا 0 باشد)، اما من فرض میکنم تتا میتواند اساساً هر زاویه‌ای باشد - من آن را برای مثبت حل میکنم، و برای مورد استفاده من انتظار دارم همیشه در $0-\pi$ باشد.
محدوده، اما حدس می‌زنم که لازم نباشد.
من از جنبه هندسی چیزها نسبتاً مطمئن هستم. که برای من منطقی است سعی کردم کاری مثل $\frac{\sin (t)}{t} = k$ انجام دهم
، اما من هنوز نمی دانم چگونه می توانم این را از نظر محاسباتی تقریب کنم - روش نیوتن $t_{k+1} = t_k - \dfrac{\sin t_k - K t_k} {\cos t_k - K}$بنابراین من طول وتر را می دانم (C) و طول قوس (Aاما مشکل داشتن R وجود داردبنابراین می توانم فرمول را کمی تغییر دهم تا برابر با صفر شود و آن را وصل کنم$0=\frac{C}{2\sin\left(\frac{360A}{4\pi R}\right)}-R$
انحنا و شعاع انحنا Curvature and radius of curvature
منحنی صفحه ای را در نظر بگیرید که با معادله y = f (x) تعریف شده است. فرض کنید که خط مماس به منحنی در نقطه M(x,y) کشیده شده است. مماس یک زاویه α با محور افقی تشکیل می دهد
]با جابجایی Δs در طول کمان منحنی، نقطه M به سمت نقطه M1 حرکت خواهد کرد. در این صورت، موقعیت خط مماس نیز تغییر می‌کند؛ زاویه شیب خط مماس بر نقطه M1 و محور مثبت x، α+Δα خواهد بود. بنابراین، با حرکت نقطه به اندازه Δs، خط مماس به اندازه Δα می‌چرخد (فرض شده که وقتی جهت حرکت زاویه α پادساعتگرد باشد، افزایشی خواهد بود.)قدر مطلق نسبت $\frac{{\Delta \alpha }}{{\Delta s}}$ انحنا یا خمیدگی متوسط کمان MM1 نامیده می‌شود. با حد$\Delta s \to 0,$، انحنای منحنی در نقطه M به صورت زیر محاسبه می‌شود:$\large K = \lim \limits _ { \Delta s \to 0 } \left | { \frac { { \Delta \alpha } } { { \Delta s } } } \right | .$برای یک منحنی مسطح با معادله y=f(x)، انحنا در نقطه M(x,y) بر حسب مشتق‌های اول و دوم تابع$y = f\left( x \right),$ و با فرمول زیر بیان می‌شود:$K = \frac{{\left| {y^{\prime\prime}\left( x \right)} \right|}}{{{{\left[ {1 + {{\left( {y'\left( x \right)} \right)}^2}} \right]}^{\frac{3}{2}}}}}.$اگر منحنی به فرم پارامتری و با معادلات x=x(t) و y=y(t) تعریف شده باشد، آنگاه انحنا در نقطه M(x,y) با رابطه زیر تعیین می‌شود:$K = \frac{{\left| {x'y^{\prime\prime} - y'x^{\prime\prime}} \right|}}{{{{\left[ {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2}} \right]}^{\frac{3}{2}}}}}.$اگر یک منحنی با معادله قطبی داده شود، انحنا با فرمول محاسبه می شود$K = \frac{{\left| {{r^2} + 2{{\left( {r'} \right)}^2} - rr^{\prime\prime}} \right|}}{{{{\left[ {{r^2} + {{\left( {r'} \right)}^2}} \right]}^{\frac{3}{2}}}}}.$شعاع هم نسبست عکس با انحنا داره$\large R = \frac { 1 } { K } .$یعنی $R = \frac{{{{\left[ {1 + {{\left( {y'\left( x \right)} \right)}^2}} \right]}^{\frac{3}{2}}}}}{{\left| {y^{\prime\prime}\left( x \right)} \right|}}.$بدیهی است که برای یافتن انحنای بیضی در نقاط و (شکل ) کافی است، زیرا به دلیل تقارن منحنی، انحنای دو راس مخالف بیضی یکسان خواهد بود.برای محاسبه انحنا، راحت است که از معادله متعارف بیضی به معادله به شکل پارامتریک عبور کنیم:$x = a\cos t,\;\;\;y = b\sin t,$پس من میام فرمول اجرا میکنم $x' = {x'_t} = \left( {a\cos t} \right)^\prime = - a\sin t,\;\;\;x^{\prime\prime} = x^{\prime\prime}_{tt} = \left( { - a\sin t} \right)^\prime = - a\cos t;$.و به طور سیمیلار برای y خوب بعد محاسبه من $K = \frac{{\left| {ab\,{{\sin }^2}t + ab\,{{\cos }^2}t} \right|}}{{{{\left( {{a^2}{{\sin }^2}t + {b^2}{{\cos }^2}t} \right)}^{\frac{3}{2}}}}} = \frac{{\left| {ab\left( {{{\sin }^2}t + {{\cos }^2}t} \right)} \right|}}{{{{\left( {{a^2}{{\sin }^2}t + {b^2}{{\cos }^2}t} \right)}^{\frac{3}{2}}}}} = \frac{{ab}}{{{{\left( {{a^2}{{\sin }^2}t + {b^2}{{\cos }^2}t} \right)}^{\frac{3}{2}}}}}.$و من دو مقدار برای t انتخاب میکنم$K\left( A \right) = K\left( {t = 0} \right) = \frac{{ab}}{{{{\left( {{a^2}{{\sin }^2}0 + {b^2}{{\cos }^2}0} \right)}^{\frac{3}{2}}}}} = \frac{{ab}}{{{{\left( {{b^2}} \right)}^{\frac{3}{2}}}}} = \frac{{ab}}{{{b^3}}} = \frac{a}{{{b^2}}};$و $K\left( B \right) = K\left( {t = \frac{\pi }{2}} \right) = \frac{{ab}}{{{{\left( {{a^2}{{\sin }^2}\frac{\pi }{2} + {b^2}{{\cos }^2}\frac{\pi }{2}} \right)}^{\frac{3}{2}}}}} = \frac{{ab}}{{{{\left( {{a^2}} \right)}^{\frac{3}{2}}}}} = \frac{{ab}}{{{a^3}}} = \frac{b}{{{a^2}}}.$انحنای ابربیضی را که با معادلات پارامتری تعریف شده است، بیابید$x\left( t \right) = a\, {\cos ^n}t,\; y\left( t \right) = b\,{\sin ^n}t,$ابربیضی ها منحنی های خوبی هستند که شکل آن ها بین دایره و مربع است. آنها کاربردهای زیادی در طراحی و مهندسی دارند.
شکل یک منحنی با انحنای آن مشخص می شود. در این مسئله، فرمول کلی انحنای یک ابربیضی با توان مثبت دلخواه را استخراج می کنیم.$K \text = \frac{{ab{2^{1 - n}}\left| {\left( {2 - n} \right){{\sin }^{n - 1}}2t} \right|}}{{{{n\left[ {{a^2}{{\cos }^{2n - 2}}t\,{{\sin }^2}t + {b^2}{{\sin }^{2n - 2}}t\,{{\cos }^2}t} \right]}^{\frac{3}{2}}}}}.$
خمیدگی در حقیقت معادل با میزان تغییر جهت یک تابع برداری یا همان تابع پارامتری نسبت به پارامتر وابسته است. روابط زیادی به منظور بدست آوردن خمیدگی توابع پارامتری وجود دارد. با این حال تعریف کلی خمیدگی به صورت زیر است.$\Large \kappa = \left | { \frac { { d \, \overrightarrow T } } { {d s } } } \right|$در رابطه فوق، s برابر با طول خم و T نشان دهنده بردار مماس به خم است. همان‌طور که در مطلب توابع برداری نیز بیان شد، به منظور بدست آوردن خمیدگی یک تابع، در ابتدا باید، آن را به صورت پارامتری بیان کرده، سپس قادر خواهیم بود تا خمیدگی آن را محاسبه کنیم.$\large \kappa = \frac{{\left\| {\overrightarrow T ^ {\prime} \left( t \right)} \right\|}}{{\left\| {\overrightarrow r ^ {\prime} \left( t \right)} \right\|}}\hspace{1.0in}\kappa = \frac{{\left\| {\overrightarrow r ^{ \prime } \left( t \right) \times \overrightarrow r ^{\prime\prime} \left( t \right)} \right\|}}{{{{\left\| {\overrightarrow r ^ {\prime} \left( t \right)} \right\|}^3}}}$اجازه دهید یک منحنی صفحه به صورت پارامتریک توسط بردار شعاع تعریف شود در حالی که یک نقطه در امتداد منحنی حرکت می کند، جهت مماس تغییر می کندانحنای منحنی را می توان به عنوان نسبت زاویه چرخش مماس به طول قوس پیموده شده این نسبت تعریف کرد.
انحنای متوسط منحنی نامیده می شود. هنگامی که نقطه به نقطه نزدیک می شود، انحنای منحنی را در نقطه به دست می آوریم$k = \lim\limits_{\Delta s \to 0} \frac{{\Delta \varphi }}{{\Delta s}} = \frac{{d\varphi }}{{ds}}.$واضح است که انحنا در حالت کلی بسته به جهت چرخش مماس می تواند مثبت یا منفی باشد.
اگر یک منحنی با بردار شعاع تعریف شود، انحنای آن توسط بردار مشخص می شود$k = \frac{{\mathbf{r'} \times \mathbf{r^{\prime\prime}}}}{{{{\left| {\mathbf{r'}} \right|}^3}}},$
اگر مختصات یک منحنی به صورت پارامتری به صورت و مشخص شود، فرمول محاسبه انحنا به شکل$k = \frac{{x'y^{\prime\prime} - y'x^{\prime\prime}}}{{{{\left[ {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2}} \right]}^{\frac{3}{2}}}}}.$در موردی که یک منحنی در مختصات قطبی به شکل داده می شود انحنای آن با عبارت تعریف می شود$k\left( \varphi \right) = \frac{{{\rho ^2} + 2{{\left( {\rho'} \right)}^2} - \rho \rho^{\prime\prime}}}{{{{\left[ {{\rho ^2} + {{\left( {\rho'} \right)}^2}} \right]}^{\frac{3}{2}}}}}.$hope I helped you understand the question. Roham Hesami,
