۱. برابری مقدار:
مقدار دو نیرو باید یکسان باشه. به عبارت دیگه، هر دو نیرو باید به یک اندازه روی جعبه اثر کنن.
۲. جهت مخالف:
دو نیرو باید به سمتهای مخالف یکدیگر عمل کنن. یعنی بردارهای نیروها باید توی خطوط متضاد باشن.
۳. محور مشترک:
دو نیرو باید روی یه محور یا راستای خاصی اعمال بشن. یعنی خط اثر نیروها باید توی یه راستا یا روی یه محور مشترک باشه.
اگه این شرایط برقرار باشن، میشه حکم کرد که دو نیرو روی یه راستا و جهت مشترک عمل میکنن و گشتاور مجازی ایجاد میشه.
در مورد جابجایی جعبه ۲ متری، از دو نیروی همپوشان (قدرت یکسان و جهت مخالف) برای جابهجایی جعبه استفاده میشه. این دو نیرو به سمتهای مختلف عمل میکنن و با هم تداخل دارند، پس میشه گفت که دو نیرو روی یه راستا و جهت مشترک عمل میکنن و گشتاور مجازی تولید میشه.
"الان دو نفر دارن با یه سوزن بازی میکنن. یکی از راست نیرو میزنه با ۱۰ نیوتن، دیگری از چپ میزنه هم با ۱۰ نیوتن. حالا میخواهیم ببینیم آیا شرایط کار مجازی دو نیرو (گشتاور مجازی) اینجا برقراره یا نه.
اولاً همه چیز یکی باشه: هر دو نیرو با یک مقدار، یعنی ۱۰ نیوتن عمل میکنن.
دوماً جهتها باید مخالف باشن: یکی به سمت راست، دیگری به سمت چپ.
سوماً محور مشترک: هر دو نیرو توی یک محور مشترک، یعنی راستای عمود بر سطح زمین، عمل میکنن.
با توجه به این حالت، میتونیم بگیم که دو نیرو در یک راستا و جهت مشترک عمل میکنن و کار مجازی دو نیرو (گشتاور مجازی) تو اینجا برقراره.
فرض کنید دو تا دوست با حرفه کار مجازی یه سوزن رو از دو سرش میگیرند و به طرف یه مرکز مشترک میندازند. یکی از سمت راست به چپ نیرو میزنه، دیگری از سمت چپ به راست نیرو میزنه، هر دو توی همون سطح سوزن. شرایط کار مجازی دو نیرو (گشتاور مجازی) اینجا هم برقراره:
هم چیز یکی باشه: هر دو نیرو با یک مقدار، یعنی ۱۰ نیوتن عمل میکنن.
جهتها مخالف باشن: یکی از راست به چپ، دیگری از چپ به راست.
محور مشترک: هر دو نیرو توی یک محور مشترک، یعنی خط مستقیم از وسط سوزن به سمت راست یا چپ، عمل میکنن.
از این رو، دو نیرو در یک راستا و جهت مشترک عمل میکنن و کار مجازی دو نیرو (گشتاور مجازی) اینجا هم برقراره."
"شرایط کار مجازی دو نیرو (گشتاور مجازی) در اینجا هم برقراره:
برابری مقدار: هر دو نیرو به اندازهی برابر، یعنی با مقادیر یکسان، عمل میکنند.
جهت مخالف: نیروها در جهات مخالف یکدیگر عمل میکنند. یکی از راست به چپ و دیگری از چپ به راست.
محور مشترک: هر دو نیرو در یک محور مشترک (خط مستقیم از وسط سوزن به سمت راست یا چپ) اعمال میشوند.
از این رو، دو نیرو در یک راستا و جهت مشترک اعمال میشوند و کار مجازی دو نیرو (گشتاور مجازی) برقراره.
حالا برای مسئلهی محاسباتی:
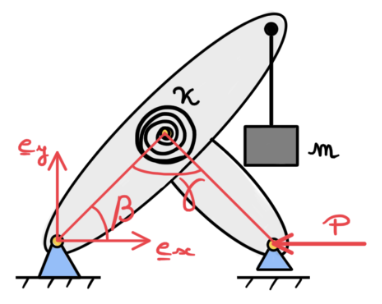
مکانیسم از دو میله جامد تشکیل شده که طولشL است
، کوتاه به طول L/2
. سیستم مرجع استفاده شده $\{\mathbf{e}_x, \mathbf{e}_y\}$ است. یک انتهای آن در امتداد سابق قفل شده $\mathbf{e}_y $ و $\mathbf{e}_x$، انتهای دیگر فقط مجاز به لغزش در امتداد سابقه
. در محل اتصال بین دو میله، یک فنر پیچشی با سفتی κ بازیگری است. فنر با زاویه $\gamma$ همراه است و برای زاویه $\gamma_0$ کشش ندارد. یک نیروی P به مکانیسم و جرم m اعمال می شود از انتهای میله بلند اویزونه تحت تأثیر نیروها، مکانیسم حرکت میکنه و حرکات آن با استفاده از زاویه β توصیف میشه
حال محاسبه پتانسیل نیروی F
مرتبط با نیروهای وارد بر مکانیسم به عنوان تابعی از L، $m$و، β.
$\begin{equation}
\mathcal{F} = -W_E
\end{equation}
$
$\begin{equation}
W_E = W_P + W_{mg} = \int \mathbf{P} \cdot \text{d}\mathbf{r}_P + \int m\mathbf{g} \cdot \text{d}\mathbf{r}_{mg}
\end{equation}$
$\begin{equation}
= \int_{\beta_0}^{\beta} \mathbf{P} \cdot \frac{\text{d}(\mathbf{r}_P)}{\text{d}\beta}\text{d}\beta
+ \int_{\beta_0}^{\beta} m \mathbf{g} \cdot \frac{\text{d}(\mathbf{r}_{mg})}{\text{d}\beta}\text{d}\beta
\end{equation}$
از تصویر می تونم بردارهای موقعیت و نیرو زیر را تشخیص دهم:
$\begin{equation}
\mathbf{P} = [-P, 0]^T
\end{equation}
$
$\begin{equation}
\mathbf{g} = [0, -g]^T
\end{equation}
$
$\begin{equation}
\mathbf{r}_P = L[\cos(\beta), 0]^T
\Longrightarrow
\frac{\text{d}(\mathbf{r}_P)}{\text{d}\beta} = L[-\sin(\beta), 0]^T
\end{equation}
$
$\begin{equation}
\mathbf{r}_{mg} = L[\cos(\beta), \sin(\beta)]^T
\Longrightarrow
\frac{\text{d}(\mathbf{r}_{mg})}{\text{d}\beta} = L[-\sin(\beta),\cos(\beta)]^T
\end{equation}$
حالا اگر این را کنار هم بگذارم
$\begin{equation}
\mathcal{F} = -W_E = -\left(\left( PL\int_{\beta_0}^{\beta} \sin(\beta) \text{d}\beta \right)+
\left( -mgL\int_{\beta_0}^{\beta} \cos(\beta) \text{d}\beta \right)\right)
\end{equation}$
اگر انتگرال ها را ارزیابی کنم
$\begin{equation}
PL\int_{\beta_0}^{\beta} \sin(\beta) \text{d}\beta = -PL \cos{\beta} \vert_{\beta=\beta_0}^{\beta}
\end{equation}$
$\begin{equation}
-mgL\int_{\beta_0}^{\beta} \cos(\beta) \text{d}\beta = -mgL\sin{\beta} \vert_{\beta=\beta_0}^{\beta}
\end{equation}$
و این میده
$\begin{equation}
\mathcal{F} = PL (\cos(\beta) - \cos(\beta_0)) +
mgL(\sin(\beta) - \sin(\beta_0))
\end{equation}$
با این حال پاسخی که کتاب درسی به من داده
$\begin{equation}
\mathcal{F} = PL (\cos(\beta) - \cos(\beta_0)) -
mgL(\sin(\beta) - \sin(\beta_0))
\end{equation}
$
من معتقدم در تعریف بردارهای موقعیت rp اشتباه کرده ام
و/یا rmg
، اما من نمی توانم اشتباه خود را پیدا کنم
$\vec{g}=(0,-g)
$
$\frac{d\vec{r}_{mg}}{d\beta}=L(-\sin\beta, \cos \beta)$
.$\vec{g}.\frac{d\vec{r}_{mg}}{d\beta}=-gL\cos \beta$
$\mathcal{F}=-W_E= \underline{+} m\int \vec{g}.\frac{d\vec{r}_{mg}}{d\beta} d\beta$


