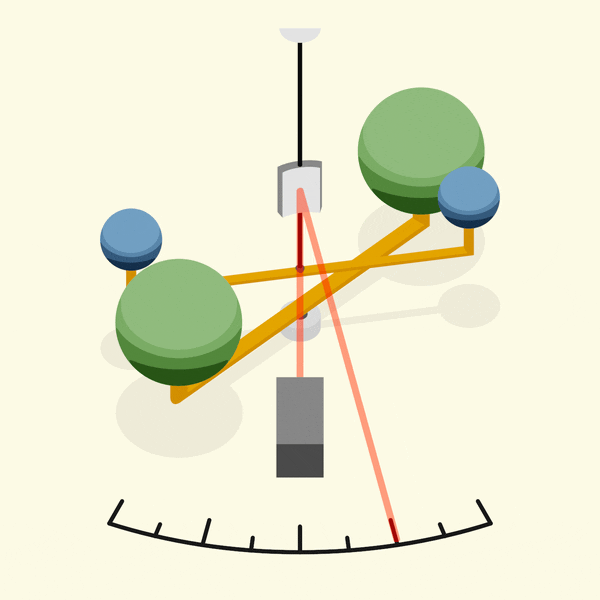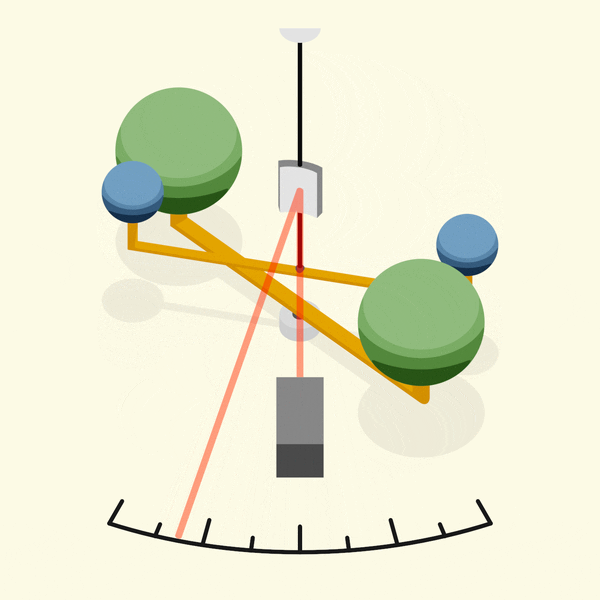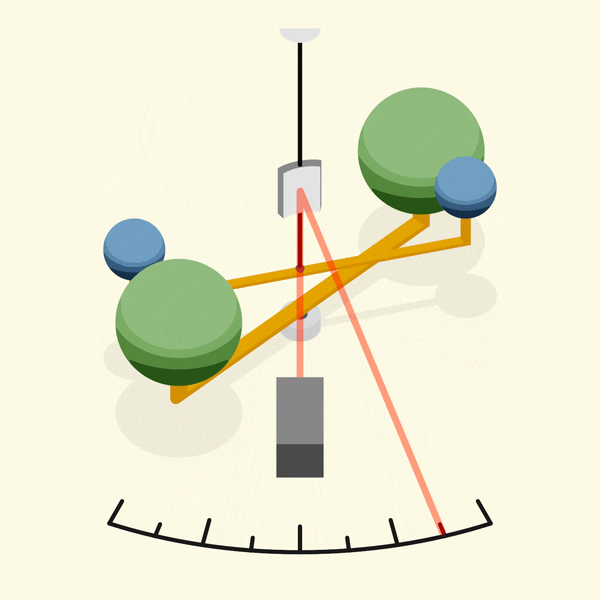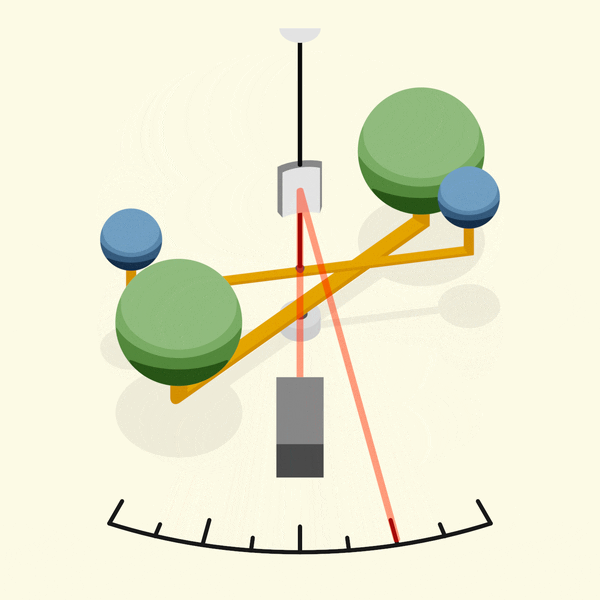
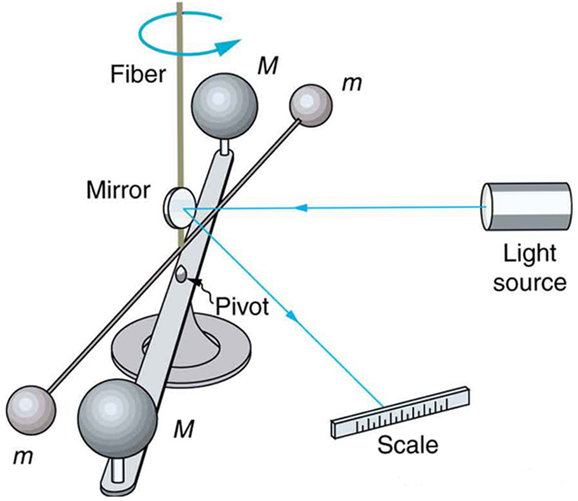
دستگاه کاوندیش از یه ساختار غیرهمسویه تشکیل شده بود که دوتا جرم بزرگتر (جرم های سنگین) داخل هر طرفش بودن. دوتا جرم کوچیکتر (جرم های کوچولوی سبک) هم به انتهای هرکدوم از جرم های بزرگتر وصل بودن. این دستگاه یه ترازوی پیچشی هم داشت.
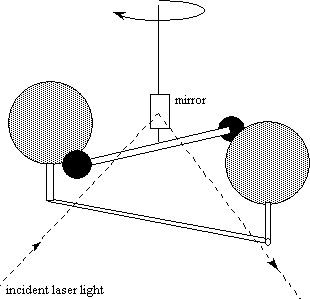
آزمایش اینجوری بوده:
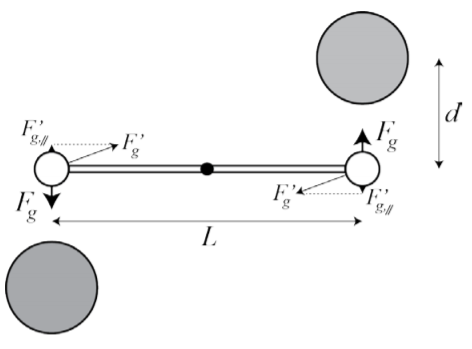
۱. جرم های کوچیک در حالت استراحت قرار گرفته بودن و ترازوی پیچشی به خاطر جاذبه از حرکتی مثل حرکتش تحت تأثیر این جرم ها دچار چرخش میشده.
۲. بعد جرمهای بزرگتر به آرامی داخل محدودهٔ جرم هاهای کوچیک میومدن. موقعیت جرم های بزرگتر تنظیم میشد که جرم های کوچیک دوباره با نیروی گرانشی بین جرم ها که توسط گشتاور تعلیق متعادل میشد، استراحت باشن.
۳. تو این حالت استراحت، ترازوی پیچشی به حرکت نمیآمد و زاویهٔ چرخشش به عنوان نتیجهای از جاذبه بین جرم ها ثابت میموند.
از این تغییرات در حرکت ترازوی پیچشی، کاوندیش گشتاور ناشی از جاذبه بین جرمها رو اندازه گیری میکرد. با استفاده از این گشتاورها و اطلاعات در مورد فواصل میان جرم ها،
کاوندیش مستقیماً ثابت گرانشی را اندازه گیری نکرد خوب اون . از ترازوی پیچشی برای اندازه گیری چگالی زمین استفاده کرد. با استفاده از نتایج کاوندیش، دیگران مقدار G را محاسبه کردند.از نوسانات میرا شده برای تعیین ثابت پیچشی تعلیق استفاده میشه. اندازه گیری ها با جرم های کوچک در ابتدا در حالت استراحت انجام میشه. جرم های بزرگتر (روی یک پایه چرخان) به آرامی وارد میشن و موقعیت آنها به گونه ای تنظیم میشه که جرم های کوچک دوباره با نیروی گرانشی بین جرم ها که توسط گشتاور تعلیق متعادل میشه در حال استراحت باشند.جایی که $F_g$ نیروی اصلیه که روی جرم های کوچکتر کار میکنه $F'_g$ بنابراین من می خواهم $F'_{g,||}$ اما هنوز نتونستم فرمولی پیدا کنم اما. را ه حل من فاصله D بین جرم کوچکتر چپ و جرم بزرگتر سمت راست $D=\sqrt{d^2+L^2}$بنابراین برای $F_g'$
من گرفتم $F_g'=G\frac{mM}{D^2}$و:
$F'_{g,||}=F_g'\sin \theta,$خوب $\tan\theta=\frac{d}{L}$یا$\sin\theta=\frac{d}{D}$زیرا $F_g=G\frac{mM}{d^2}$
من حتی میتونم $\frac{F'_{g,||}}{F_g}$ را تعیین کنم$\frac{F'_{g,||}}{F_g}=\frac{d^3}{(d^2+L^2)^{\frac32}}$
روش زیر روشی نیست که کاوندیش استفاده کردش،دستگاه کاوندیش اساساً از دو جفت کره تشکیل شده بود که هر جفت دمبل هایی را تشکیل میدن که دارای یک محور چرخشی مشترک هستند یک دمبل از سیمی آویزان است و با چرخوندنش ازاد میشه خوب. مقدار پیچ و تاب که با موقعیت یک نقطه نور منعکس شده از یک آینه میشه. دمبل دوم را می توان طوری چرخوند که هر یک از کره های آن در مجاورت یکی از کره های دمبل دیگر باشند. جاذبه گرانشی بین دو مجموعه کره سیمو را میپیچه و اندازهگیری این پیچشه که امکان محاسبه بزرگی نیروی گرانش را فراهم میکنه.خوب میدونیم از قانون هوک، گشتاور روی سیم پیچش متناسب با زاویه انحرافه
${\displaystyle \theta }$ مقدار. گشتاوره گشتاور اعمال شده ناشی از جاذبه گرانشی $τ=κθ $که θ حداکثر زاویه انحراف نقطه نورانیه. در این حداکثر انحرافه نیروی بین یک کره بزرگ و یک کره کوچکه حداکثر انحراف جایی که r فاصله بین مراکز کره است. این به گشتاور با $τ=F(L/2)$ مربوط میشه که L طول دمبل کوچکه. خوب اینجا ثابت گرانشی را میشه حساب کرد
ببینین دوستان هوپایی من که با چرخش آینه از طریق یک زاویه θ، نور بازتاب شده در 2θ حرکت میکنه. بنابراین با معکوس کردن دمبل زاویه 4θ اندازه گیری میشه
${\displaystyle \kappa \theta } $که در آن
${\displaystyle \kappa }$ ضریب پیچش سیمه. با این حال، گشتاور در جهت مخالف نیز توسط کشش گرانشی اجرام ایجاد میشه. می توان آن را به عنوان حاصل ضرب نیروی جاذبه یک توپ بزرگ روی یک توپ کوچک و فاصله L/2 تا سیم تعلیق نوشت. از آنجایی که دو جفت توپ وجود داره که هر یک از آنها نیروی F را در فاصله ای حس میکنندL/2 از محور تعادل، گشتاور ناشی از نیروی گرانشی LF است. در حالت تعادله (زمانی که تعادل در یک زاویه تثبیت شده باشه
${\displaystyle \theta }$، مقدار کل گشتاور باید صفر باشه زیرا این دو منبع گشتاور تعادل دارن. حوب حالا میتونم بزرگی آنها را با فرمول بالا برابر کنم که بهدست میادش${\displaystyle \kappa \theta \ =LF\,}$برای F، قانون گرانش جهانی نیوتن برای بیان نیروی جاذبه بین یک توپ بزرگ و کوچک استفاده میشه
${\displaystyle F={\frac {GmM}{r^{2}}}\,}$جایگزینی F به معادله اول بالا به دست میده
${\displaystyle \kappa \theta \ =L{\frac {GmM}{r^{2}}}\qquad \qquad \qquad (1)\,}$
برای پیدا کردن ضریب پیچش هم ${\displaystyle \kappa }$ سیم کاوندیش دوره نوسان رزونانس طبیعی T تعادل پیچشی را اندازه گرفتش
${\displaystyle T=2\pi {\sqrt {\frac {I}{\kappa }}}}$
با فرض اینکه جرم خود پرتو پیچشی ناچیزه ممان اینرسی تعادل فقط به دلیل توپ های کوچیکه. در نظر گرفتن آنها به عنوان جرم های نقطه ای هر کدام در $L/2 $از محورمحاسبه میشه
${\displaystyle I=m\left({\frac {L}{2}}\right)^{2}+m\left({\frac {L}{2}}\right)^{2}=2m \left({\frac {L}{2}}\right)^{2}={\frac {mL^{2}}{2}}\,}$،
و به همین صورت هم${\displaystyle T=2\pi {\sqrt {\frac {mL^{2}}{2\kappa }}}\,}$
حل این برای${\displaystyle \kappa }$، با جایگزینی به (1)، و مرتب سازی مجددش برای Gاین نتیجه رو میده بهمون
${\displaystyle G={\frac {2\pi ^{2}Lr^{2}\theta }{MT^{2}}}\,}$.هنگامی که G پیدا شدش میتونین از جاذبه یک جسم در سطح زمین به خود زمین برای محاسبه جرم و چگالی زمین استفاده کنین
${\displaystyle mg={\frac {GmM_{\rm {earth}}}{R_{\rm {earth}}^{2}}}\,}$
${\displaystyle M_{\rm {earth}}={\frac {gR_{\rm {earth}}^{2}}{G}}\,}$
${\displaystyle \rho _{\rm {earth}}={\frac {M_{\rm {earth}}}{{\tfrac {4}{3}}\pi R_{\rm {earth}}^{ 3}}}={\frac {3g}{4\pi R_{\rm {earth}}G}}\,}$