فرض کنید با خمیر، استوانه ای به شعاع
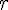
و طول
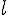
ساخته ایم.
حجم و مساحت آن عبارت است از:
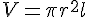
و
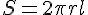
استوانه را تغییر شکل می دهیم، طوری که شعاعش،
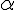
برابر
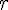
شود. (
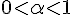
)
از آنجایی که حجم ثابت مانده، پس طول و مساحت جدید عبارتند از:
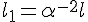
،
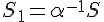
باز نازکترش می کنیم، طوری که شعاع جدید،
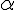
برابر شعاع قبلی شود.
حجم ثابت مانده و مساحت عبارت است از:
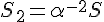
اگر به همین نازک کردن ادامه دهیم در
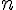
اُمین مرحله، حجم ثابت است
و مساحت عبارت است از:
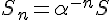
پس در بینهایت حجم ثابت می ماند ولی مساحت بی نهایت می شود.
این شیپور هم همین گونه است. گویی یک تکه آدامس به جایی چسبیده
و می گیریم و می کشیم. نازک و نازکتر می شود و در عین حال حجمش
ثابت ولی سطحش مدام بزگتر می شود.
مرکز جرم آن واگراست. به جایش می توانیم مرکز جرم "وو وو زلا"
را که از دوران خم
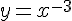
ساخته می شود، پیدا کنیم.
---------------------------------------------------------------------------
این شکل به شیپور جبرئیل معروف است (Gabriel's Horn)
در مسیحیت و یهودیت برخلاف اسلام، این جبرئیل است که به جای
اسرافیل (=رافائل) در روز رستاخیز، برای زنده کردن مردگان، در صور می دمد.

