مشکل100 زندانی- چرا این راه حل کار نمی کنه؟
زندانیان این فرصت را دارند که استراتژی خود را از قبل طراحی کنند، و به آن نیاز خواهند داشت، زیرا اگر هر زندانی نام خود را پیدا نکند، همه متعاقبا اعدام خواهند شد.
یک استراتژی برای آنها بیابید که احتمال موفقیت (بقای همه زندانیان) بیش از 30٪ باشد.
نظر: اگر هر زندانی مجموعه تصادفی 50 جعبه را بررسی کند، احتمال زنده ماندن آنها $1 /2^{100} \approx 0.0000000000000000000000000000008$
. آنها می توانند بدتر از این کار کنند - اگر همه آنها در 50 جعبه یکسان نگاه کنند، شانس آنها به صفر می رسد. 30٪ به نظر مسخره دور از دسترس به نظر می رسد - اما بله، مشکل را درست شنیدید.
بنابراین تعداد جایگشت های با چرخه طولانی استراه حل
ابتدا راه حل را توضیح می دهم، سپس توضیح می دهم که چرا کار می کند.

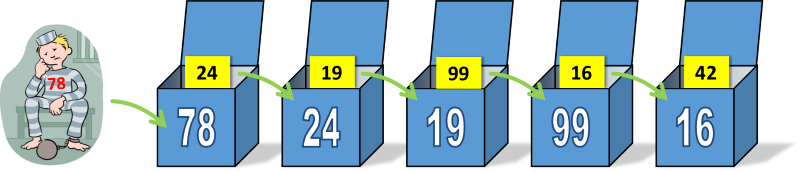
استراتژی به طرز شگفت انگیزی ساده است. اول از همه شما کادر مربوط به شماره خودتان را باز می کنید. اگر بلیط خود را پیدا کردید، عالی است!، در غیر این صورت، شماره بلیط را در جعبه خود جستجو کنید و این همان جعبه است. شما این استراتژی را ادامه می دهید ... راه خود را از طریق جعبه ها به زنجیر می زنید. خودشه!
در نهایت، یا شماره خود را پیدا خواهید کرد، یا از محدودیت 50 جعبه عبور خواهید کرد. در ابتدا، به نظر می رسد که این نباید در مقایسه با انتخاب ساده جعبه ها به طور تصادفی تفاوتی ایجاد کند (و برای هر فردی، من درست می گویم)، اما از آنجایی که همه 100 زندانی از یک مجموعه جعبه استفاده خواهند کرد، باعث می شود یک تفاوت بزرگ
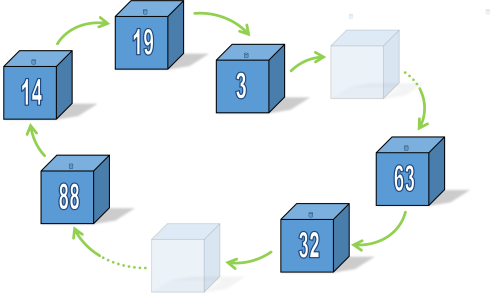
زیبایی این معما دانستن راه حل نیست، بلکه دانستن این است که چرا راه حل کار می کند!فقط یک اشاره گر در داخل، و یک اشاره گر از هر جعبه وجود دارد اگر جعبه ای تک تن نباشد (میزبان بلیط خود را داشته باشد)، به صورت زنجیره ای خواهد بود. برخی از زنجیرها ممکن است به اندازه دو جعبه کوتاه باشند، برخی دیگر ...
از آنجایی که زندانی از جعبه شماره خود شروع می کند، طبق تعریف، در زنجیره ای هستند که حاوی بلیط آنها است (تنها یک بلیط وجود دارد که به آن جعبه اشاره می کند).

با دنبال کردن زنجیره اطراف تضمین می شود که با دنبال کردن زنجیره به بلیط خود ختم می شوند.
تنها سوال این است که آیا آنها می توانند قبل از باز شدن پنجاه جعبه این کار را انجام دهند!
طول زنجیر
برای موفقیت همه، حداکثر طول زنجیره باید کمتر از پنجاه جعبه باشد. اگر یک زنجیر بزرگتر از پنجاه جعبه باشد، آنهایی که بلیط خود را در آن زنجیره دارند شکست می خورند (و در نتیجه همه می میرند).
اگر حداکثر طول زنجیره کمتر از پنجاه جعبه باشد، پس همه موفق می شوند!
یک لحظه در مورد آن فکر کنید، در هر پیکربندی فقط یک زنجیره می تواند طولانی تر از پنجاه جعبه باشد (در مجموع فقط صد جعبه وجود دارد، بنابراین اگر یک زنجیره بلندتر از 50 باشد، زنجیر دیگر باید کمتر باشد. در مجموع بیش از 50).
احتمال یک زنجیره بلند
بعد از اینکه خودتان را متقاعد کردید که برای موفقیت، حداکثر طول زنجیره باید کمتر یا مساوی 50 باشد و در هر مجموعه ای که زنجیره ای بیشتر از پنجاه دارد فقط یک زنجیره می تواند وجود داشته باشد،
توزیع احتمال طول طولانی ترین چرخه یک جایگشت تصادفی از اعداد 1 تا 100. منطقه سبز با احتمال بقای زندانیان مطابقت دارد.
در مسئله اولیه، 100 زندانی موفق هستند اگر طولانی ترین چرخه جایگشت حداکثر 50 طول داشته باشد. بنابراین احتمال بقای آنها برابر است با احتمال اینکه یک جایگشت تصادفی از اعداد 1 تا 100 شامل هیچ چرخه ای با طول بیشتر نباشد. از 50. این احتمال در ادامه مشخص می شود.
جایگشت اعداد 1 تا 100 می تواند حداکثر یک چرخه طول داشته باشد L > 50 l> 50. دقیقا وجود دارد روشهای$ {\tbinom {100}{l}}$ برای انتخاب اعداد چنین چرخهای (به ترکیب مراجعه کنید). در این چرخه، این اعداد را می توان در مرتب کرد (l-1)! راه هایی از آنجایی که وجود دارد جایگشت l برای نشان دادن چرخه های متمایز طول l به دلیل تقارن چرخه ای. اعداد باقی مانده را می توان در مرتب کرد
$(100-l)!$ راه ها. بنابراین، تعداد جایگشت های اعداد 1 تا 100 با چرخه طول $l>50 $برابر است با
${\displaystyle {\binom {100}{l}}\cdot (l-1)!\cdot (100-l)!={\frac {100!}{l}}.}$
احتمال اینکه یک جایگشت تصادفی (به طور یکنواخت) حاوی هیچ چرخه ای با طول بیشتر از 50 نباشد، با فرمول رویدادهای منفرد و فرمول رویدادهای تکمیلی محاسبه می شود.
${\displaystyle 1-{\frac {1}{100!}}\left({\frac {100!}{51}}+\ldots +{\frac {100!}{100}}\right)=1-\left({\frac {1}{51}}+\ldots +{\frac {1}{100}}\right)=1-(H_{100}-H_{50})\approx 0.31183,}$جایی که
H_{n} عدد هارمونیک n. بنابراین، با استفاده از استراتژی پیروی از چرخه، زندانیان در 31 درصد موارد شگفتآور زنده میمانند.اعداد هارمونیک تقریباً با مساحت زیر هذلولی داده می شوند و بنابراین می توان آنها را با یک لگاریتم تقریب زد.
اگر 2n به جای 100 زندانی در نظر گرفته شده است که در آن
در یک عدد طبیعی دلخواه، احتمال بقای زندانیان با استراتژی پیروی از چرخه با${\displaystyle 1-(H_{2n}-H_{n})=1-(H_{2n}-\ln 2n)+(H_{n}-\ln n)-\ln 2.}$برقرار است، که منجر به احتمال بقا مجانبی از$\lim _{{n\to \infty }}(H_{n}-\ln n)=\gamma $و${\displaystyle \lim _{n\to \infty }(1-H_{2n}+H_{n})=1-\gamma +\gamma -\ln 2=1-\ln 2\approx 0.30685.}$ز آنجایی که توالی احتمالات به طور یکنواخت در حال کاهش است، زندانیان با استراتژی پیروی از چرخه در بیش از 30 درصد موارد مستقل از تعداد زندانیان زنده می مانند
چرا این کار می کند؟
هر جعبه حاوی یک بلیط است و بلیط ها منحصر به فرد هستند. این بدان معنی است که یا یک بلیط در کادر صحیح قرار دارد یا به کادر دیگری اشاره می کند. از آنجایی که بلیط ها متمایز هستند، فقط یک بلیط وجود دارد که به هر جعبه اشاره می کند (و فقط یک راه برای رسیدن به هر جعبه).اگر در مورد آن فکر کنید، جعبه ها زنجیره های دایره ای را تشکیل می دهند. یک جعبه فقط می تواند بخشی از یک زنجیره بکا باشد
$\frac{100!}{100} + \frac{100!}{99} + \ldots + \frac{100!}{51}$این از مجموع$100!$ئ
$\frac{1}{100} + \frac{1}{99} + \ldots + \frac{1}{51}$از نظر عددی، این حدود 0.6882 است، یعنی شانس موفقیت حدود 31.18٪ است، کمی بیش از 30٪ لازم.
به طور کلی، نسبت جایگشت های ناموفق برای N
زندانیان $H_N - H_{N/2}$ است
جایی که $H_n = 1 + \frac{1}{2} + \ldots + \frac{1}{n}$
n نامیده می شودعدد هارمونیک ام برای مقادیر بزرگ n
، $H_n \approx \ln n + C$
برای تعدادی عدد C و سری $H_N - H_{N/2}$
به $\ln 2 \approx 0.6931$ همگرا می شود$\begin{align}H_n - H_{n/2} = \big(\!\ln(n) + C\big) - \big(\!\ln(n/2) + C\big) \\$
یک معمای ترکیبی وجود دارد که به شرح زیر است: در این مشکل، 100 زندانی شماره گذاری شده برای زنده ماندن باید شماره های خود را در یکی از 100 کشو پیدا کنند. قوانین می گوید که هر زندانی می تواند تنها 50 کشو باز کند و نمی تواند با زندانیان دیگر ارتباط برقرار کند.
بهترین راه حلی که تاکنون یافت شده این است که: 1. هر زندانی ابتدا کشو را با شماره خود باز می کند. 2. اگر این کشو شامل شماره او باشد کارش تمام شده و موفق بوده است. 3. در غیر این صورت، کشو حاوی شماره زندانی دیگر است و سپس با این شماره کشو را باز می کند. 4. زندانی مراحل 2 و 3 را تکرار می کند تا زمانی که شماره خود را پیدا کند یا 50 کشو را باز کند.
از طریق این فرآیند، تا زمانی که یک چرخه بیش از 50 نفر وجود نداشته باشد، شانس نسبتاً بالایی (تقریباً 30٪) برای موفقیت زندانیان وجود دارد. این به این دلیل است که تقریباً 70٪ احتمال دارد که یک چرخه 51 یا بیشتر وجود داشته باشد.
وقتی سعی می کردم احتمال وجود یک چرخه 51 یا بیشتر را محاسبه کنم، زندانی را مجبور کردم که از کشوی خودش شروع کند. احتمال اینکه کشو شامل شماره او نباشد باید 99/100 باشد. در چنین حالتی به سراغ کشوی دوم می رود (که شماره آن در کشو اول پیدا شده است). احتمال اینکه این کشو شامل شماره او نباشد 98/99 است. بنابراین احتمال اینکه او قبل از یافتن شماره خود از 51 کشو یا بیشتر عبور کند، به نظر من باید 99/100 * 98/99 * 97/98 *...*49/50 باشد. بنابراین، احتمال وجود یک چرخه با اندازه 51 یا بیشتر توسط این زنجیره استدلال 49/100 خواهد بود.
من امیدوار بودم که بپرسم آیا کسی در اینجا می تواند به من بگوید نقص در خط استدلال من وجود دارد.
اجازه دهید روشی برای محاسبه تعداد جایگشت ها در Sn ارائه کنم
که حاوی یک k هستند چرخه زمانی که $2k>n$ واضح است که حداکثر یکی از این چرخه ها می تواند وجود داشته باشد، ما می توانیم آن را در $\binom{n}{k}\times (k-1)!$ انتخاب کنیم!
روش ها و سپس عناصر باقی مانده را در (n-k) جایگشت!
راه ها.
همچنین توجه می کنیم که احتمال 51،52،… یا 100 چرخه وجود فقط مجموع احتمالات فردی است زیرا این رویدادها متقابلاً منحصر به فرد هستند.
بنابراین احتمال شکست زندانیان عبارت است از:
$\sum\limits_{k=51}^{100} \frac{\frac{100!(k-1)!(100-k)!}{k!(100-k)!}}{100!}=\sum\limits_{k=51}^{100} \frac{(k-1)!}{k!}=\sum\limits_{k=51}^{100} \frac{1}{k}\approx 0.688$
نقص شما تا حدودی شبیه پارادوکس تولد است: هر زندانی خاص 49/100 شانس دارد که در زنجیره ای از 51 نفر یا بیشتر باشد. اما احتمال اینکه حداقل یک زندانی در زنجیره ای از 51 نفر یا بیشتر باشد حدود 70 درصد است. رفتن از دو مورد اول، دومی پیچیده است، زیرا احتمالات مستقل نیستند: اگر یک زندانی در یک سیکل 51 یا بیشتر باشد، حداقل 50 زندانی دیگر نیز در سیکل های 51 یا بیشتر هستند.
اما من فکر می کنم نیاز به تأکید بیشتری دارد: وابستگی کلید اصلی است. با فرض اینکه جایگشت اعداد کاملاً تصادفی است، مهم نیست که اولین زندانی کدام نیمی از کشوها را باز کند - تا زمانی که اینها 50 کشو مختلف باشند (بدیهی است که دو بار باز کردن یک کشو کمتر از حد مطلوب است)، احتمال پیدا کردن شماره او دقیقاً وجود دارد. 1/2
هر کاری که می کند نکته کلیدی در وابستگی به انتخاب زندانیان است.
فرض کنید که P(Ai) این احتمال است که i زندانی شماره اش را پیدا کرد. همانطور که مشاهده کردیم P(A1)=1/2 ، اما در واقع P(Ai)=1/2 برای هر i . با این حال، از آنجایی که زندانیان می توانند انتخاب خود را بر اساس جایگشت پنهان در کشوها انجام دهند، می توانند Ai را مجبور کنند.
و Aj وابسته بودن و تمرکز خرابی ها بر روی یک مجموعه خاص از جایگشت ها.دقیق تر، مجموعه همه جایگشت های ممکن در کشوها را در نظر بگیرید$\Omega = \{\pi_1, \pi_2, \ldots\}$
،بیایید جایگشتی را $\pi$ بنامیم موفق برای iاگر استراتژی جستجوی او موفق به یافتن شماره خود شود،$\Omega_k$ را تعریف کنید به عنوان مجموعهای از جایگشتها که برای همه زندانیان در محدوده {1،…،k} موفق هستند.
.احتمال پایه به ما $P(A_1) = \frac{|\Omega_1|}{|\Omega|} = \frac{1}{2}$ می دهد
. حال، اگر زندانی دوم به صورت تصادفی انتخاب کند، $\Omega_1$ را تقسیم میکند بیشتر از نصف، که اندازه $\Omega_2$ است
نصف اندازه \Omega_1$ $خواهد بود
و یک چهارم Ω
. از سوی دیگر، با تعدیل استراتژی خود، یعنی با در نظر گرفتن جایگشتی که مشاهده می کند، زندانی دوم می تواند سعی کند موفقیت های خود را بر جایگشت های $\Omega_1$ متمرکز کند.
و شکست او در جایگشت در $\Omega \setminus \Omega_1$. به این ترتیب $|\Omega_2|$ به شدت بزرگتر از $|\Omega| / 4$ است، اگرچه کوچکتر از |Ω1|
. اگر همه زندانیان از این روش پیروی کنند، وقتی یکی شکست میخورد، بسیاری دیگر نیز شکست میخورند، اما وقتی یکی موفق میشود، بسیاری دیگر نیز موفق خواهند شد.
در نهایت برای اینکه بفهمید چرا کشوهای خاص باز شده اهمیت چندانی ندارد (یعنی چرا کمتر از وابستگی مهم است): فرض کنید که ما زندانیان را مجبور میکنیم بر روی یک تغییر دلخواه σ به توافق برسند.
و یک استراتژی را دنبال کنید که در آن i"زندانی با $\sigma(i)$ شروع می شود و وقتی x را پیدا کرد
در کشو، با $\sigma(x)$ دنبال می شود. این استراتژی چیزی را در احتمالات تغییر نمی دهد - زیرا جایگشت $\pi$
در کشوها تصادفی است، احتمال$\pi \circ \sigma$ دارای چرخه ای به طول ≥51 همچنین کمتر از 70 درصد است. در حالی که هیچ زندانی نمی تواند از قبل متعهد به باز کردن مجموعه ای از کشوها شود، کشوهای باز شده به دلیل σ است.، به نوعی خودسرانه.
یک پازل دیگر نیز وجود دارد که از تکنیک مشابهی استفاده می کند. 100 زندانی وجود دارند که کلاه سیاه یا سفید به سر دارند (تکلیف خودسرانه، بدون محدودیت شمارش). همه همدیگر را می بینند، اما نه رنگ کلاهشان. هر کدام روی یک کاغذ می نویسند (برای اینکه بقیه نبینند) فکر می کنند چه رنگی کلاه دارند. اگر همه درست حدس زده باشند، رایگان هستند. بهترین استراتژی برای حدس زدن رنگ کلاه توسط زندانیان چیست؟
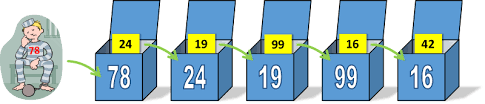
روشدوم
مقدمه: شرح مشکل اصلی را می توان در ویکی پدیا یافت. بهترین استراتژی این است: هر زندانی ابتدا کشو را با شماره خود باز می کند و سپس هر کشوی بعدی با شماره ای که قبلا پیدا شده است تعیین می شود. با این استراتژی، آنها فقط در صورتی از بین می روند که چرخه ای با طول بیشتر از 50 وجود داشته باشد
(نگاشت اعداد به کشوها). همانطور که در نسخه کارگردان مخرب توضیح داده شد، اگر تعداد زندانیان به طور تصادفی توزیع نشود، اما به شکلی هدفمند چنین چرخه ای با طول بیش از 50 ایجاد کند.
، سپس زندانیان می توانند با برچسب زدن مجدد به طور تصادفی کشوها با این کار مقابله کنند.
من به نوع دیگری از مشکل علاقه مند هستم، که در آن پس از اینکه یک زندانی باز کردن کشوها را (با موفقیت) تمام کرد، به همه زندانیان منتظر گفته می شود که زندانی چند کشو را باز کرده است. زندانیان منتظر می توانند از این اطلاعات برای تصمیم گیری در مورد برچسب گذاری مجدد کشوها استفاده کنند یا خیر.
اگر اولین زندانی n را باز کرده باشد کشوها (n≤50، این بدان معنی است که یک چرخه به طول n وجود دارد و زندانیان منتظر اکنون باید احتمال مشروط را تعیین کنند که علاوه بر چرخه طول n
چرخه دیگری با طول بیشتر از 50 وجود دارد؛ اگر آن احتمال بزرگتر از احتمال اصلی باشد$\sum_{k=51}^{100}\frac{1}{k}$ ، سپس آنها باید کشوها را دوباره برچسب بزنند. اجازه دهید N
تعداد زندانیان باشد (N=100)، A رویدادی که یک چرخه به طول $n\leq \frac{N}{2}$ توسط اولین زندانی گزارش می شود و B رویدادی که چرخه ای با طول بیشتر از N/2 باشد وجود دارد. سپس زندانیان باید تخمین بزنند:
$P(B|A) = \frac{P(A\cap B)}{P(A)}$
برای تخمین P(A)، می توان تعداد جایگشت هایی را در نظر گرفت که (حداقل یک) چنین چرخه ای را در مقایسه با تعداد کل جایگشت ها $N!$. این شامل انتخاب n است
از N کشوها، سپس اعداد آنها و همچنین شماره سایر کشوها را به طور دلخواه تغییر دهید:
$P(A) = \frac{{N \choose n} n! (N-n)!\frac{1}{n}}{N!} = \frac{1}{n}$
فاکتور $\frac{1}{n}$
در صورت حساب این واقعیت است که n وجود دارد جایگشت های متمایز که چرخه یکسانی را ایجاد می کنند (فقط اعداد را از یک کشو به کشو دیگر منتقل می کنند). با این حال، به نظر نمی رسد که این نتیجه برای n=1 صحیح باشد احتمال P(A) 1 خواهد بود که اشتباه است بنابراین فکر میکنم این رویکرد درستی است، اما نمیتوانم بفهمم روش صحیح تخمین P(A) چیست.
و P(A∩B)یک پاسخ ساده برای این وجود دارد که نیازی به محاسبه ندارد، با فرض اینکه رویکرد اصلی برای N بهینه است
زندانیان / کشوها زمانی که اطلاعات اضافی داده نمی شود.
بیایید بگوییم K اول گزارش شده است که زندانیان $n_1,\ldots,n_k\le 50$ را باز کرده اند
هر کدام کشوها از این، مشخص می شود که چرخه هایی با طول های $n_1,\ldots,n_k$ وجود دارد
، که برخی از آنها ممکن است با کشوهایی در همان چرخه مطابقت داشته باشند.
حال، فرض کنیم S تعداد کل کشوهایی است که باز شده است. ممکن است تعداد دقیق آن برای زندانیان ناشناخته باشد، مگر اینکه عدد نیک باشد
همه متمایز هستند: اگر$n_i=n_j$
آنها نمی دانند که آیا زندانی i و J بخشی از یک چرخه یا دو چرخه متفاوت هستند. با این حال، آنها می دانند که$\sum_{n\in\{n_1,\ldots,n_k\}} n\le S\le\sum_i n_i$
، که باید مثبت باشد. این S کشوها همه بخشی از چرخه هایی با طول ≤50 هستندو این کشوها همگی «امن» هستند، زندانی با آن شمارهها هم همینطور است، حتی اگر نداند شمارههای «ایمن» کدام است.
چیزی که نامشخص باقی می ماند، چرخه های 100-S باقی مانده است کشوها با این حال، هیچ چیز در مورد این کشوها مشخص نیست زیرا هیچ یک از آنها هنوز باز نشده است: یعنی آنها هنوز به اندازه قبل تصادفی هستند، فقط کمتر. بنابراین اگر راه حل اصلی برای هر تعداد کشو بهینه است، پس باید برای 100-S بهینه باشد
کشوهااگر $100-S$ کشوها باز نشده می مانند، یعنی پس از حذف کشوهایی که قبلاً باز شده اند و مشخص شده است که بخشی از چرخه های "ایمن" هستند، احتمال داشتن یک چرخه با طول بیش از 50 وجود دارد. در $100-S$ کشوهای تصادفی کمتر از 100 است
کشوهای تصادفی، بنابراین تصادفی کردن شماره یک استراتژی بد خواهد بود.
مشکل P(A) شما تخمین این است که شما چند جایگشت را چندین بار می شمارید - اگر جایگشت دو چرخه به طول n داشته باشد.
، سپس آن را دو بار می شمارید (برای هر دو چرخه).روش استاندارد برای تخمین احتمال قرار گرفتن نقطه تصادفی در چرخه طول n به شرح زیر است: ابتدا N دارد
گزینه هایی که باید به کجا برود، و می تواند به هر یک از N-1 برود
(به جز اولیه)، سپس بعدی باید به یکی از N-2 برود از N-1 گزینه ها و غیره تا n-نقطه باید به 1 برود گزینه باقی ماندن N−n+1
. با ضرب،$\frac{N - 1}{N} \cdot \frac{N - 2}{N - 1} \cdot \ldots \cdot \frac{1}{N - n + 1} = \frac{1}{N}$به دست میآید
.با این حال، شما حتی به آن نیاز ندارید، می توانید P(B|A) را محاسبه کنید.
به طور مستقیم. فقط توجه داشته باشید که بعد از اینکه چرخه ای به طول n را آشکار کردیم
، بقیه N−n عناصر یک جایگشت با توزیع یکنواخت دیگر را تشکیل می دهند، و بنابراین احتمال داشتن یک چرخه با طول حداقل 50 وجود دارد.
دوباره$H_{N - n} - H_{50}$ است
.100 زندانی مشکل 100 جعبه، محاسبه احتمال تک زندانی
تلاش برای درک راه حل برای یک زندانی مجرد در معمای 100 زندانی در صورت انتخاب تصادفی، بسیار ساده است 1/2
اما اگر از روشی که در محلول توضیح داده شده استفاده کند (به دنبال چرخه جایگشت) باز هم 1/2 است
${\displaystyle (1-\ln(2))\cdot 1+\sum _{k=\lfloor n/2\rfloor +1}^{N}{\frac {1}{k}}\left(1-{\frac {k}{n}}\right)=1-\ln(2)+\sum _{\lfloor n/2\rfloor +1}^{N}{\frac {1}{k}}-\sum _{k=\lfloor n/2\rfloor +1}^{N}{\frac {1}{n}}=1-\ln(2)+\ln(2)-{\frac {1}{2}}={\frac {1}{2}}}$
چگونه این فرمول را به دست آوردند؟ یا چرا هنوز 1/2 است؟
هنوز 1/2 است
زیرا در نظر گرفتن یک زندانی منزوی که 50 جعبه از 100 جعبه را بدون اطلاعات اضافی باز می کند، همیشه 50 جعبه خواهد داشت.
///این (فرض کنید) احتمال این است که چرخه یک نقطه به طور تصادفی انتخاب شده در یک جایگشت تصادفی (از N=100 امتیاز) کمتر یا مساوی N/2=n=50 باشد. این دقیقاً احتمال زنده ماندن یک زندانی بر اساس استراتژی چرخه در مسئله اصلاح شده است که در آن بقای هر زندانی به بقای سایر زندانیان بستگی ندارد.
می توانید سعی کنید آن را با محاسبه احتمال اینکه چرخه 0 در یک جایگشت تصادفی (یکنواخت) اعداد 0 ... 99 طولانی تر از 50 باشد، ساده کنید. می توانید بنویسید:
$P(\textrm{prisoner doesn't survive} ) = P(\textrm{cycle of 0 is longer than n} ) = \sum_{k=n+1}^{N}P(\textrm{exists a cycle of length k and 0 is in that cycle}) = \sum_{k=n+1}^{N}\frac{k}{N}P(\textrm{exists a cycle of length k}) = \sum_{k=n+1}^{N}\frac{k}{N} \frac{1}{k} = \sum_{k=n+1}^{N}\frac{1}{N} = \frac{N-n}{N}=\frac{100-50}{100}=\frac{1}{2}.$
توجه داشته باشید که اگر چرخه ای به طول k>n وجود داشته باشد
، پس باید چرخه منحصربهفردی باشد که طولانیتر از n باشد (همه چرخههای دیگر میتوانند حداکثر N-k طول داشته باشند)، بنابراین احتمال k/N برای 0 وجود دارد. در مرحله احتمال وجود یک چرخه k برابر 1/k از این استفاده کردیم: احتمال چرخه طولm


