نیروی اویلر
-
the love of god
نام: سرباز البرت
عضویت : شنبه ۱۳۹۲/۴/۱۵ - ۱۰:۱۵
پست: 46-
سپاس: 13
نیروی اویلر
سلام. ببخشید کسی درباره ی نیروی اویلر چیزی میدونه اگه میدونید شرایط ایجاد موهمی بودن یا نبودن ان را توضیح دهید.
-
غلامعلی نوری
عضویت : سه‌شنبه ۱۳۹۱/۴/۲۰ - ۰۸:۵۱
پست: 1201-
سپاس: 885
- جنسیت:
تماس:
Re: نیروی اویلر
درودthe love of god نوشته شده:سلام. ببخشید کسی درباره ی نیروی اویلر چیزی میدونه اگه میدونید شرایط ایجاد موهمی بودن یا نبودن ان را توضیح دهید.
نيرويي كرانه اي ( افقي) است كه ستون بر ( عمودبر ) نيروي گريز از ميانه است
-
rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سه‌شنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3289-
سپاس: 5494
- جنسیت:
تماس:
Re: نیروی اویلر
تو مکانیکی که میخونم نیروی اویلر یه شبه‌نیروی مماسیه که در مقابل هر شتاب شعاعی احساس میشه. بهش شتاب عکس‌العمل شتاب اویلر میگیم ببین این شتاب همچنین شتاب سمتی یا شتاب عرضی هم میگیم دوست هوپایی من .نیروی اویلر یکی از سه نیروی ساختگیه که در فریم مرجع چرخان پیدا میشه بقیه نیروهای گریز از مرکز و کوریولیس هستن. این بستگی به شتاب زاویه ای فریم مرجع در حال چرخش و موقعیت یک ذره در اون فریم داره ببین تومکانیک نیروی اویلر نیروی مماسی ساختگیه که زمانی ظاهر میشه که از یک فریم مرجع غیریکنواخت چرخان برای تحلیل حرکت استفاده میشه و در سرعت زاویه‌ای محورهای فریم مرجع تغییراتی وجود دارده${\displaystyle \mathbf {F} _{\mathrm {Euler} }=m\mathbf {a} _{\mathrm {Euler} }=-m{\frac {d{\boldsymbol {\omega }}}{dt}}\times \mathbf {r} .}
$ مثالا نیروی اویلر توسط شخصی که سوار بر چرخ و فلکه احساس میشه. با شروع سواری نیروی اویلر نیروی ظاهریه که فرد را به پشت اسب هل میده. و هنگامی که سواری متوقف میشه این نیروی ظاهری فرد را به سمت جلوی اسب هل میده. فردی که سوار بر اسب نزدیک به محیط چرخ و فلکه نیروی ظاهری بیشتری نسبت به شخصی که سوار بر اسبی نزدیک به محور چرخشه درک میکنه.
جهت و بزرگی شتاب اویلر در فریم مرجع چرخان هم
${\mathbf {a}}_{{\mathrm {Euler}}}=-{\frac {d{\boldsymbol \omega }}{dt}}\times {\mathbf {r}},$که در آن ω سرعت زاویه ای چرخش فریم مرجع و r موقعیت برداری نقطه در فریم مرجع است. نیروی اویلر بر جسمی به جرم m در فریم مرجع در حال چرخشه
${\mathbf {F}}_{{\mathrm {Euler}}}=m{\mathbf {a}}_{{\mathrm {Euler}}}=-m{\frac {d{\boldsymbol \omega }}{dt}}\times {\mathbf {r}}.$
قانون اول اویلر بیان میکنه که سرعت تغییر تکانه خطی p جسم صلب برابره با برآیند تمام نیروهای خارجی Fext که بر جسم وارد میشن${\displaystyle F_{\text{ext}}={\frac {d\mathbf {p} }{dt}}.}
$نیروهای داخلی بین ذرات تشکیل دهنده یک جسم به تغییر تکانه جسم کمکی نمیکنند چون نیرویی برابر و مخالف وجود داره و در نتیجه هیچ اثر خالصی وجود نداره
قانون دوم اویلر بیان میکنه که تغییر تکانه زاویه ای L در نقطه ای که در یک فریم مرجع اینرسی (اغلب مرکز جرم جسم) ثابته برابره با مجموع گشتاورهای خارجی نیروی (گشتاور) وارد شده در جسم M در آاون نقطه${\displaystyle \mathbf {M} ={d\mathbf {L} \over dt}.}
$ . برای اجسام صلب که فقط در دو بعد از انتقال میچرخن این میتونه ${\displaystyle \mathbf {M} =\mathbf {r} _{\rm {cm}}\times \mathbf {a} _{\rm {cm}}m+I{\boldsymbol {\alpha }}،}$باشه
ببین توزیع نیروهای داخلی در یک جسم تغییر شکل پذیر حتما در سرتاسر یکسان نیستش یعنی تنش ها از یک نقطه به نقطه دیگر متفاوته من مثال میزنم یک میله انعطاف پذیر بلند با جرم یکنواخت را تصور کن میله توسط یک محور در مرکز خود پشتیبانی می شود و در حالت تعادل است. چگونه توضیح دهیم که چرا میله در انتهای دور افتاده است؟
اگر FBD free body diagram از موقعیت را رسم کنم وزن و نیروی تماس معمولی هر دو در محور چرخش متعادل میشن. پس چرا خم شدن میله در انتهای آن وجودداره
معادله یک میله انعطاف پذیر $E\,I\,\frac{d^4 w(x)}{dx^4}=q\tag 1$
جایی که w(x) انحراف میله q بار توزیع شده E مدول الاستیک I ممان دوم${\textstyle I=\iint _{R}x^{2}\,dA,}$ سطح مقطع میلیه وجود مقداری وزن در انتها و اینکه خود میله نمیتواند تمام وزن را تحمل کنه باعث تغییر شکل آن میشود و همانطور که قبلاً گفتم این هیچ قانونی را نقض نمیکنه زیرا نه تنها اعمال نیرو بلکه گشتاور نیز اهمیت داره. هر بخش جرم اولیه dm میله در فاصله r از یک نقطه محوری تحت تأثیر گشتاور اولیه قرار میگیره $d\vec \tau = \vec r \times d\vec F = \vec r \times \vec g~dm$
گشتاور تا انتهای میله افزایش مییابه بنابراین میله مانند یک سهمی خم میشه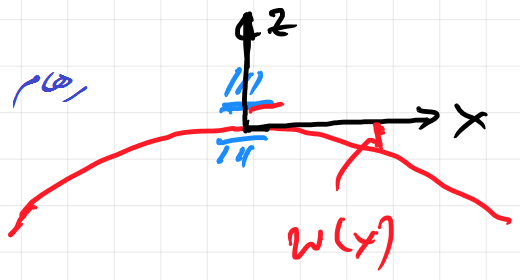
. این تغییر نیروهای داخلی در سراسر جسم توسط قانون حرکت دوم نیوتن در مورد بقای تکانه خطی و تکانه زاویه ای کنترل میشه خوب با یک ذره جرمی اعمال میشه اما در مکانیک پیوسته به جسمی با جرمی متصل میشه. . برای اجسام پیوسته این قوانین را قوانین حرکت اویلر میگیم.${\mathbf F}_{B}=\int _{V}{\mathbf b}\,dm=\int _{V}{\mathbf b}\rho \,dV$
که در آن b نیروی وارد بر جسم در واحد جرمه و dm = ر dV عنصر جرمی بی نهایت کوچک جسمه .نیروهای جسم و نیروهای تماسی که بر روی جسم وارد میشن باعث ایجاد گشتاورهای متناظر آن نیروها نسبت به یک نقطه معین میشن. پس مجموع گشتاور اعمال شده M در مورد مبدا هم ${\mathbf M}={\mathbf M}_{B}+{\mathbf M}_{C}
$که در آن MB و MC ممان های ناشی از جسم و نیروهای تماس را نشون میدن.پس مجموع تمام نیروها و گشتاورهای اعمال شده با توجه به مبدأ سیستم مختصاتکه بر روی بدنه اعمال میشه را می توان به عنوان مجموع یک انتگرال حجم و سطح محاسبه کرد${\displaystyle \mathbf {F} =\int _{V}\mathbf {a} \,dm=\int _{V}\mathbf {a} \rho \,dV=\int _{S}\mathbf {t} \,dS+\int _{V}\mathbf {b} \rho \,dV}
$و${\displaystyle \mathbf {M} =\mathbf {M} _{B}+\mathbf {M} _{C}=\int _{S}\mathbf {r} \times \mathbf {t} \,dS+\int _{V}\mathbf {r} \times \mathbf {b} \rho \,dV.}$
معادلات حرکت اویلر برای جسم صلب و نیروهای اینرسی
مجموع گشتاورها برابره با نرخ تغییر تکانه زاویه ای جسم در فریم چرخان.پس آیا لازم نیست نیروهای اینرسی را هنگام محاسبه گشتاورها در مختصات دوار در نظر بگیرم؟
آیا لازم نیست نیروهای اینرسی را هنگام محاسبه گشتاورها در مختصات دوار در نظر بگیرم؟
اما یک گشتاور اینرسی وجود داره از دید یک فریم اینرسی مقیاس چرخشی قانون دوم نیوتن برای چرخش حول مرکز جرمه
$\frac{d\boldsymbol L}{dt} = \sum_i \boldsymbol \tau_{\text{ext},i}\tag{roham1}$جایی که L تکانه زاویه ای جسم نسبت به اینرسیه
گشتاور خارجی و جدا از دید اینرسیه. توجه که این مربوط به اجسام غیر صلب و همچنین اجسام صلبه.
رابطه بین مشتق زمانی هر کمیت برداری q از دید فریم های اینرسی و چرخشی
$\left(\frac{d\boldsymbol q}{dt}\right)_\text{inertial} =
\left(\frac{d\boldsymbol q}{dt}\right)_\text{rotating} + \boldsymbol \Omega \times \boldsymbol q\tag{2}$جایی که Ω
نرخ چرخش فریم با توجه به اینرسیه برای یک جسم صلب تکانه زاویه ای جسم نسبت به اینرسی اما در مختصات ثابت جسم بیان میشه $\boldsymbol L = \mathbf I\,\boldsymbol \omega$است.
جایی که I ممان اینرسی جسم از تانسور اینرسی و ω سرعت چرخش جسم با توجه به اینرسیه اما در مختصات ثابت جسم بیان میشه. از آنجایی که تانسور اینرسی جسم صلب در فریم ثابت بدنه ثابته داریم
$\left(\frac{d\boldsymbol L}{dt}\right)_\text{body roham-fixed} = \frac{d(\mathbf I \boldsymbol \omega)}{dt} = \mathbf I \frac{d\boldsymbol\omega}{dt}\tag{roham3}$
ترکیب معادلات (1)، (2) و (3) نتیجه میده
$\mathbf I \frac{d\boldsymbol\omega}{dt} = \sum_i \boldsymbol \tau_{\text{ext},i} - \boldsymbol \omega\times(\mathbf I \times \boldsymbol \omega)\tag{4}$
این معادلات حرکت اویلر برای یک جسم صلبه. با این حال عبارت$-\boldsymbol \omega\times(\mathbf I \times \boldsymbol \omega)$
در اصل یک گشتاور اینرسیه. همانطور که نیروهای اینرسی در فریم های اینرسی ناپدید میشن این گشتاور اینرسی نیز ناپدید میشه
نیروی اویلر برای آونگ
من یک سوال در رابطه با نیروی اویلر دارم. چرا این نیرو هرگز برای یک آونگ ساده در نظر گرفته نمیشود؟
تا آنجا که من متوجه شدم نیروی اویلر با (فرض کنید آونگ 2 بعدی را در یک فضای سه بعدی در نظر بگیرم که کمیت ها بردار هستن) داده میشود.
$\begin{equation}
\boldsymbol{\dot{\omega}} \times \mathbf{r}
\end{equation}$این به معنای ناپدید شدن نیرو $\boldsymbol{\dot{\omega}} = 0$ است
، یا r=0 ، یا بردارها باید در یک جهت باشند. من نمی دانم چرا یکی از این شرایط برآورده شده .این یک شبه نیروی اینرسیه که وقتی در یک چارچوب غیر گالیله ای قرار داره ایجاد میشود. ω سپس سرعت شعاعی فریم مرجع شما نسبت به یک فریم گالیلیه. اینجا اینطور نیست.
اگر ناظری در انتهای آونگ خود بزارم تجربیات انجام شده در آن باید آن را در نظر بگیرم
درباره $\frac{d L}{d t}=\tau$ در یک مرکز چرخشی فریم جرمی
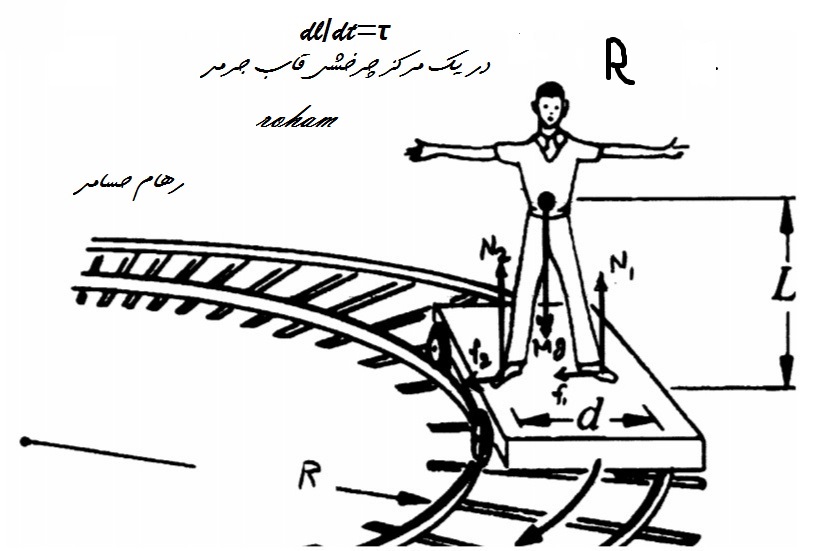
رهام با جرم M روی واگن راه آهنی ایستاده که یک پیچ بدون کرانه به شعاع R را با سرعت v می‌چرخونه. من رو به جهت حرکته
گشتاور مرکز جرم برابره $-N_{1} \frac{d}{2}+N_{2} \frac{d}{2}+\left(f_{1}+f_{2}\right) L=0$
سوالم $-N_{1} \frac{d}{2}+N_{2} \frac{d}{2}+\left(f_{1}+f_{2}\right)L=0$
معادله فوق از مرکز جرم رهام به عنوان نقطه ای استفاده میکنه که معادله $\frac{d L}{d t}=\tau$ استفاده شده
این معادله در یک فریم اینرسی درسته اما مرکز جرم چرخان و در نتیجه غیر اینرسیه پس چگونه معادله صحیح است؟این معادله در یک فریم اینرسی درسته اما مرکز جرم چرخان و در نتیجه غیر اینرسیه پس چگونه معادله صحیح است؟
مرکز جرم به خودی خود فقط یک نقطیه هیچ فریم منحصر به فردی به مرکز جرم متصل نیست. معمولا وقتی میگیم فریم COM هیچ چرخشی وجود نداره و فریمی را می گیریم که در همه زمان ها مرکز جرم آن در مبدأ باشه
اساساً وقتی نیروی خالص صفره محاسبه گشتاور در مورد هر نقطه از فضا باید مطابقت داشته باشه. بنابراین یک فریم اینرسی بگیرم و گشتاورهای مربوط به COM را محاسبه کنم من میتونم گشتاور را با توجه به هر نقطه داده شده در هر سیستم مختصات معین محاسبه کنم. به طور خاص می تواید گشتاور را نسبت به مرکز جرم با تمام بردارهای نمایش داده شده در سیستم مختصات اینرسی محاسبه کنم. فقط به این دلیل که نقطه ای را برای محاسبه گشتاور با توجه به آن انتخاب میکنم به این معنی نیست که باید سیستم مختصات را تغییر بدم و آن را به آن نقطه منتقل کنم. فقط باید حاصل ضربات بردارهایی را بگیرم که از نقطه انتخاب شده به نقاطی که در آن نیروهای مختلف اعمال میشه اشاره کرده و آنها را با هم جمع کنم معادله دیفرانسیل که من اشاره کردم به یک سیستم مختصات اینرسی نیاز داره. در یک غیر اینرسی من فقط باید آن را با گشتاورهای ساختگی مربوطه اصلاح کنم تا چیزی شبیه به این $\text{Inertial: } \frac{d \vec{L}}{dt} \, = \, \vec{\tau}$
$\text{Non-inertial: } \frac{d \vec{L}}{dt} \, = \, \vec{\tau} \, + \, \vec{\tau}_{\text{fict}}$
به عنوان مثال، در دینامیک جسم صلب در یک فریم اینرسی من دارم
$\frac{d \vec{L} }{dt} \, = \, \vec{\tau}$اما در فریم محکم به جسم وصل شده و در مرکز جرم قرار داره
$\frac{d \vec{L}}{ dt} \, = \, \vec{\tau} \, + \, \vec{L} \times \vec{\omega}$جایی که $\vec{\omega}$
سرعت زاویه ای است که در فریم ثابت جسم بیان میشه. $\vec{L}$
و $\vec{\tau}$ همچنین در فریم ثابت بدن بیان میشن
من یک گاری دارم که بالای آن رهام خودم ثابتم که به طور یکنواخت در امتداد دایره ای به شعاع R حرکت میکنم با سرعت ثابت مقدار v اجازه بدین یک سیستم مختصات اینرسی را ثابت کنم در مرکز قوس دایره ای تشکیل شده توسط ریل قطار، x و y محورهای مختصات هم تراز با زمین و z محور عمود بر آن $\vec{r} \, = \, \vec{r}(t)$ بردار باشه که از مبدأ سیستم به نمایان شدن مرکز جرمم روی گاری اشاره میکنه (گاری از مسیرهای قطار دایره ای در x,y پیروی میکنه
صفحه افقی). سپس چون گاری به طور یکنواخت در امتداد یک دایره $\frac{d^2\vec{r}}{dt^2} \, = \, - \frac{v^2}{R^2} \vec{r}$
سرعت زاویه ای گاری در سیستم اینرسیه $\vec{\omega} \, = \, \frac{v}{R} \, \vec{e}_z$از آنجایی که من نسبت به گاری بی حرکتم یعنی همان طور که گاری حرکت میکنه، سرعت زاویه ایم نسبت به سیستم اینرسی برابر با سرعت زاویه ای گاری ω هستش در نتیجه، تکانه زاویه ای رهام در سیستم مختصات اینرسی به نظر میرسه
$\vec{L} \, = \, I \,\vec{\omega}\,= \, I_{z} \, \frac{v}{R} \, \vec{e}_z$جایی که$I_z$
ممان اینرسی رهامه که در امتداد محور عمودی که از مرکز جرمم می گذره محاسبه میشه که همیشه با z موازیه.
محور سیستم مختصات اینرسی بنابراین $I_z$ ثابت است این پیکربندی خاص خاصه. اگر من به نحوی کج شده بودم به طوری که محورهای اینرسیم مانند دیاگرام FBD نبود آنگاه معادله به یک جمله اضافی برای یک تکانه زاویه ای در حال تغییر زمان نیاز داشت. اما به دلیل نحوه ایستادن رهام روی گاری تکانه زاویه ای و سرعت زاویه ای در یک راستا قرار میگیرند . این به این دلیله که یک محور اینرسی مرد با z- ترازه
محور مختصات سیستم مختصات اینرسی در حالی که دو محور اینرسی دیگر همیشه به موازات x،y- میچرخند.صفحه مختصات سیستم مختصات اینرسی.
نیروهایی که در سیستم مختصات اینرسی بر روی رهام روی گاری وارد میشن هستند
$N_1 \vec{e}_z, \,\,\, N_2 \vec{e}_z, \,\,\, - \, \frac{f_1}{R}\vec{r}, \,\,\, - \, \frac{f_2}{R}\vec{r}, \,\,\, -\,\vec{mg}\,\vec{e}_z$
بردار $\vec{r}_G$ از مبدأ سیستم مختصات تا مرکز جرم منه $\vec{r}_G \, = \, \vec{r} \, + \, L \, \vec{e}_z$
بردارها از مبدأ دستگاه مختصات تا پایم هستند
$\vec{r}_1 \, =\, \left(1 + \frac{d}{2R}\right)\vec{r}$
$\vec{r}_2 \, =\, \left(1 - \frac{d}{2R}\right)\vec{r}$
زیرا$|\vec{r}| = R$ و بنابراین $\frac{\vec{r}}{R}$
یک بردار واحد است که با $\vec{r}$تراز شده
در همه زمان ها t.و$\vec{r}_i \, = \, \vec{r} \,\pm\, \frac{d}{2} \, \frac{\vec{r}}{R}$
بنابراین بردارها از مرکز جرم انسان تا پاهای او هستند
$\vec{r}_1 - \vec{r}_G \, = \,\,\, \left(1 + \frac{d}{2R}\right)\vec{r} \, - \, \vec{r} \, - \, L \, \vec{e}_z \, = \, \frac{d}{2R}\,\vec{r} \, - \, L \, \vec{e}_z$
$\vec{r}_2 - \vec{r}_G \, = \, \left(1 - \frac{d}{2R}\right)\vec{r} \, - \, \vec{r} \, - \, L \, \vec{e}_z \, = \, -\, \frac{d}{2R}\,\vec{r} \, - \, L \, \vec{e}_z$
حالا بیایید گشتاورها را محاسبه کنم
$(\vec{r}_1 - \vec{r}_G) \times ( \,N_1\,\vec{e}_z \,) \, = \, \frac{N_1d}{2R} \,\vec{r} \times \vec{e}_z$
$(\vec{r}_2 - \vec{r}_G) \times ( \,N_2\,\vec{e}_z \,) \, = \, - \, \frac{N_2d}{2R} \,\vec{r} \times \vec{e}_z$
$(\vec{r}_1 - \vec{r}_G) \times \left( \, - \, \frac{f_1}{R}\vec{r} \,\right) \, = \, \frac{f_1L}{R} \,\vec{e}_z \times \vec{r}$
$(\vec{r}_2 - \vec{r}_G) \times \left( \, - \, \frac{f_2}{R}\vec{r} \,\right) \, = \, \frac{f_2L}{R} \,\vec{e}_z \times \vec{r}$
گشتاور ثقل نسبت به مرکز جرم صفر است.
بنابراین معادله برداری حرکت برای تکانه زاویه ای / سرعت زاویه ایه
$\frac{d}{dt} \vec{L} \, = \,\frac{d}{dt}\left( I_{z} \, \frac{v}{R} \, \vec{e}_z\right) \,= \, \frac{N_1d}{2R} \,\vec{r} \times \vec{e}_z \, - \, \frac{N_2d}{2R} \,\vec{r} \times \vec{e}_z \,+\,\frac{f_1L}{R} \,\vec{e}_z \times \vec{r} \, +\, \frac{f_2L}{R} \,\vec{e}_z \times \vec{r}$
با این حال از آنجایی که $\frac{v}{R}$ ثابته
$\frac{d}{dt}\left( I_{z} \, \frac{v^2}{R} \, \vec{e}_z\right) \,= \, 0 \, = \, \left(\,- \, \frac{N_1d}{2R} \, + \, \frac{N_2d}{2R} \,+\,\frac{f_1L}{R} \, +\, \frac{f_2L}{R} \,\right) \, \vec{e}_z \times \vec{r}$ که میده
$- \, \frac{N_1d}{2R} \, + \, \frac{N_2d}{2R} \,+\,\frac{f_1L}{R} \, +\, \frac{f_2L}{R} \, = \, 0$و اگر هر دو طرف هویت دوم را در R ضرب کنم
، دقیقاً دریافت میکنم
$- \, \frac{N_1d}{2} \, + \, \frac{N_2d}{2} \,+\, ({f_1} \, +\, {f_2})\,L \, = \, 0$
بنابراین حدس میزنم دلیلی داره اگر حرکت در امتداد دایره یا حرکت کلی تر گاری شتاب میگرفت کل گشتاور صفر نمیشد. تنها دلیلی که معادله دوم برقراره اینه که سرعت زاویه ای و تکانه زاویه ای بردارهای ثابتی برای این حرکت یکنواخت خاص در طول یک دایره هستند!
بگذارید موقعیت مبدا $\mathbf{r}_{0}$ باشه
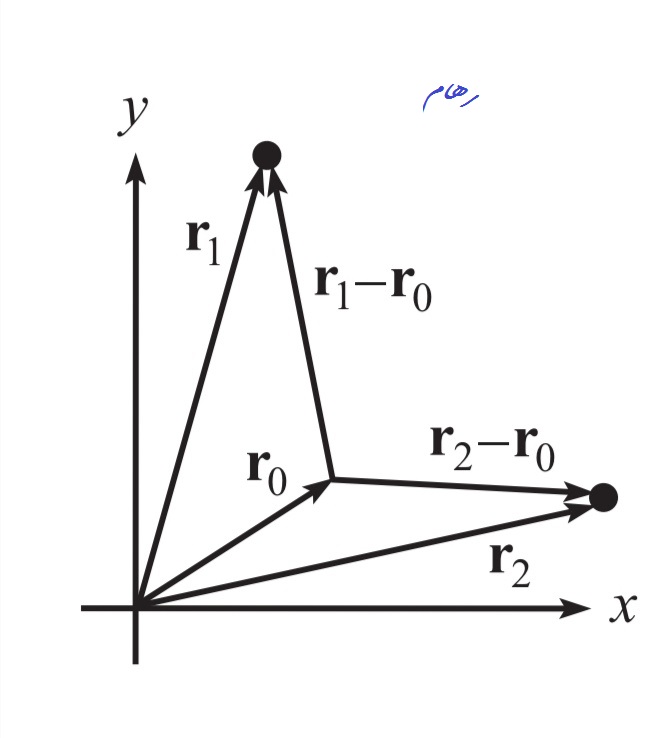و اجازه دهید موقعیت ذرات $\mathbf{r}_{i}$ باشه
. بردارهای $\mathbf{r}_{0}$
و$\mathbf{r}_{i}$ با توجه به یک سیستم مختصات ثابت معین اندازه گیری می شوند. تکانه زاویه ای کل سیستم، نسبت به مبدا (احتمالاً شتاب دهنده) $\mathbf{r}_{0}$
، است
$\mathbf{L}=\sum_{i}\left(\mathbf{r}_{i}-\mathbf{r}_{0}\right) \times m_{i}\left(\dot{\mathbf{r}}_{i}-\dot{\mathbf{r}}_{0}\right)$از این رو،
$\begin{aligned}
\frac{d \mathbf{L}}{d t} &=\frac{d}{d t}\left(\sum_{i}\left(\mathbf{r}_{i}-\mathbf{r}_{0}\right) \times m_{i}\left(\dot{\mathbf{r}_{i}}-\dot{\mathbf{r}}_{0}\right)\right) \\
&=\sum_{i}\left(\dot{\mathbf{r}}_{i}-\dot{\mathbf{r}}_{0}\right) \times m_{i}\left(\dot{\mathbf{r}_{i}}-\dot{\mathbf{r}}_{0}\right)+\sum_{i}\left(\mathbf{r}_{i}-\mathbf{r}_{0}\right) \times m_{i}\left(\ddot{\mathbf{r}_{i}}-\ddot{\mathbf{r}}_{0}\right) \\
&=0+\sum_{i}\left(\mathbf{r}_{i}-\mathbf{r}_{0}\right) \times\left(\mathbf{F}_{i}^{\mathrm{ext}}+\mathbf{F}_{i}^{\mathrm{int}}-m_{i} \ddot{\mathbf{r}}_{0}\right)
\end{aligned}$چون$m_{i} \ddot{\mathbf{r}}_{i}$
نیروی خالص است (یعنی $\mathbf{F}_{i}^{\text {ext }}+\mathbf{F}_{i}^{\text {int }}$
) عمل بر روی i ذره ام $\mathbf{F}_{i}^{\mathrm{int}}$ است
ناپدید میشه (همانطور که باید بررسی کنم). و چون $\sum m_{i} \mathbf{r}_{i}=M \mathbf{R}$
(که در آن $M=\sum m_{i}$ جرم کل است و R موقعیت مرکز جرم است)، داریم
$\frac{d \mathbf{L}}{d t}=\left(\sum_{i}\left(\mathbf{r}_{i}-\mathbf{r}_{0}\right) \times \mathbf{F}_{i}^{\mathrm{ext}}\right)-M\left(\mathbf{R}-\mathbf{r}_{0}\right) \times \ddot{\mathbf{r}}_{0}$اولین عبارت در اینجا گشتاور خارجی است که نسبت به مبدا $\mathbf{r}_{0}$ اندازه گیری میشود
. اگر هر یک از سه شرط زیر برآورده شود ناپدید میشه
$\mathbf{R}=\mathbf{r}_{0}$
، یعنی مبدا CM است.$\vec{r}_{0}=0$یعنی مبدأ شتاب نداره
$\left(\mathbf{R}-\mathbf{r}_{0}\right.$
) موازی $\ddot{\mathbf{r}}_{0}$ است. این شرایط به ندرت مورد استناد قرار میگیره
اگر هر یک از این شرایط برآورده شد من میتونم بنویسم
$\frac{d \mathbf{L}}{d t}=\sum\left(\mathbf{r}_{i}-\mathbf{r}_{0}\right) \times \mathbf{F}_{i}^{\mathrm{ext}} \equiv \sum_{i} \tau_{i}^{\mathrm{ext}}$
در این مسئله من چارچوب مرجع را در مرکز جرم دارم از این رو حالت 1 اعمال میشه و میتونم$\frac{d L}{d t}=\tau$بنویسم.
در مورد مرکز جرم از آنجایی که$\frac{d L}{d t}$ در فریم COM صفره و به معادله مورد نیاز $\tau$ =0 میرسم
$ مثالا نیروی اویلر توسط شخصی که سوار بر چرخ و فلکه احساس میشه. با شروع سواری نیروی اویلر نیروی ظاهریه که فرد را به پشت اسب هل میده. و هنگامی که سواری متوقف میشه این نیروی ظاهری فرد را به سمت جلوی اسب هل میده. فردی که سوار بر اسب نزدیک به محیط چرخ و فلکه نیروی ظاهری بیشتری نسبت به شخصی که سوار بر اسبی نزدیک به محور چرخشه درک میکنه.
جهت و بزرگی شتاب اویلر در فریم مرجع چرخان هم
${\mathbf {a}}_{{\mathrm {Euler}}}=-{\frac {d{\boldsymbol \omega }}{dt}}\times {\mathbf {r}},$که در آن ω سرعت زاویه ای چرخش فریم مرجع و r موقعیت برداری نقطه در فریم مرجع است. نیروی اویلر بر جسمی به جرم m در فریم مرجع در حال چرخشه
${\mathbf {F}}_{{\mathrm {Euler}}}=m{\mathbf {a}}_{{\mathrm {Euler}}}=-m{\frac {d{\boldsymbol \omega }}{dt}}\times {\mathbf {r}}.$
قانون اول اویلر بیان میکنه که سرعت تغییر تکانه خطی p جسم صلب برابره با برآیند تمام نیروهای خارجی Fext که بر جسم وارد میشن${\displaystyle F_{\text{ext}}={\frac {d\mathbf {p} }{dt}}.}
$نیروهای داخلی بین ذرات تشکیل دهنده یک جسم به تغییر تکانه جسم کمکی نمیکنند چون نیرویی برابر و مخالف وجود داره و در نتیجه هیچ اثر خالصی وجود نداره
قانون دوم اویلر بیان میکنه که تغییر تکانه زاویه ای L در نقطه ای که در یک فریم مرجع اینرسی (اغلب مرکز جرم جسم) ثابته برابره با مجموع گشتاورهای خارجی نیروی (گشتاور) وارد شده در جسم M در آاون نقطه${\displaystyle \mathbf {M} ={d\mathbf {L} \over dt}.}
$ . برای اجسام صلب که فقط در دو بعد از انتقال میچرخن این میتونه ${\displaystyle \mathbf {M} =\mathbf {r} _{\rm {cm}}\times \mathbf {a} _{\rm {cm}}m+I{\boldsymbol {\alpha }}،}$باشه
ببین توزیع نیروهای داخلی در یک جسم تغییر شکل پذیر حتما در سرتاسر یکسان نیستش یعنی تنش ها از یک نقطه به نقطه دیگر متفاوته من مثال میزنم یک میله انعطاف پذیر بلند با جرم یکنواخت را تصور کن میله توسط یک محور در مرکز خود پشتیبانی می شود و در حالت تعادل است. چگونه توضیح دهیم که چرا میله در انتهای دور افتاده است؟
اگر FBD free body diagram از موقعیت را رسم کنم وزن و نیروی تماس معمولی هر دو در محور چرخش متعادل میشن. پس چرا خم شدن میله در انتهای آن وجودداره
معادله یک میله انعطاف پذیر $E\,I\,\frac{d^4 w(x)}{dx^4}=q\tag 1$
جایی که w(x) انحراف میله q بار توزیع شده E مدول الاستیک I ممان دوم${\textstyle I=\iint _{R}x^{2}\,dA,}$ سطح مقطع میلیه وجود مقداری وزن در انتها و اینکه خود میله نمیتواند تمام وزن را تحمل کنه باعث تغییر شکل آن میشود و همانطور که قبلاً گفتم این هیچ قانونی را نقض نمیکنه زیرا نه تنها اعمال نیرو بلکه گشتاور نیز اهمیت داره. هر بخش جرم اولیه dm میله در فاصله r از یک نقطه محوری تحت تأثیر گشتاور اولیه قرار میگیره $d\vec \tau = \vec r \times d\vec F = \vec r \times \vec g~dm$
گشتاور تا انتهای میله افزایش مییابه بنابراین میله مانند یک سهمی خم میشه
. این تغییر نیروهای داخلی در سراسر جسم توسط قانون حرکت دوم نیوتن در مورد بقای تکانه خطی و تکانه زاویه ای کنترل میشه خوب با یک ذره جرمی اعمال میشه اما در مکانیک پیوسته به جسمی با جرمی متصل میشه. . برای اجسام پیوسته این قوانین را قوانین حرکت اویلر میگیم.${\mathbf F}_{B}=\int _{V}{\mathbf b}\,dm=\int _{V}{\mathbf b}\rho \,dV$
که در آن b نیروی وارد بر جسم در واحد جرمه و dm = ر dV عنصر جرمی بی نهایت کوچک جسمه .نیروهای جسم و نیروهای تماسی که بر روی جسم وارد میشن باعث ایجاد گشتاورهای متناظر آن نیروها نسبت به یک نقطه معین میشن. پس مجموع گشتاور اعمال شده M در مورد مبدا هم ${\mathbf M}={\mathbf M}_{B}+{\mathbf M}_{C}
$که در آن MB و MC ممان های ناشی از جسم و نیروهای تماس را نشون میدن.پس مجموع تمام نیروها و گشتاورهای اعمال شده با توجه به مبدأ سیستم مختصاتکه بر روی بدنه اعمال میشه را می توان به عنوان مجموع یک انتگرال حجم و سطح محاسبه کرد${\displaystyle \mathbf {F} =\int _{V}\mathbf {a} \,dm=\int _{V}\mathbf {a} \rho \,dV=\int _{S}\mathbf {t} \,dS+\int _{V}\mathbf {b} \rho \,dV}
$و${\displaystyle \mathbf {M} =\mathbf {M} _{B}+\mathbf {M} _{C}=\int _{S}\mathbf {r} \times \mathbf {t} \,dS+\int _{V}\mathbf {r} \times \mathbf {b} \rho \,dV.}$
معادلات حرکت اویلر برای جسم صلب و نیروهای اینرسی
مجموع گشتاورها برابره با نرخ تغییر تکانه زاویه ای جسم در فریم چرخان.پس آیا لازم نیست نیروهای اینرسی را هنگام محاسبه گشتاورها در مختصات دوار در نظر بگیرم؟
آیا لازم نیست نیروهای اینرسی را هنگام محاسبه گشتاورها در مختصات دوار در نظر بگیرم؟
اما یک گشتاور اینرسی وجود داره از دید یک فریم اینرسی مقیاس چرخشی قانون دوم نیوتن برای چرخش حول مرکز جرمه
$\frac{d\boldsymbol L}{dt} = \sum_i \boldsymbol \tau_{\text{ext},i}\tag{roham1}$جایی که L تکانه زاویه ای جسم نسبت به اینرسیه
گشتاور خارجی و جدا از دید اینرسیه. توجه که این مربوط به اجسام غیر صلب و همچنین اجسام صلبه.
رابطه بین مشتق زمانی هر کمیت برداری q از دید فریم های اینرسی و چرخشی
$\left(\frac{d\boldsymbol q}{dt}\right)_\text{inertial} =
\left(\frac{d\boldsymbol q}{dt}\right)_\text{rotating} + \boldsymbol \Omega \times \boldsymbol q\tag{2}$جایی که Ω
نرخ چرخش فریم با توجه به اینرسیه برای یک جسم صلب تکانه زاویه ای جسم نسبت به اینرسی اما در مختصات ثابت جسم بیان میشه $\boldsymbol L = \mathbf I\,\boldsymbol \omega$است.
جایی که I ممان اینرسی جسم از تانسور اینرسی و ω سرعت چرخش جسم با توجه به اینرسیه اما در مختصات ثابت جسم بیان میشه. از آنجایی که تانسور اینرسی جسم صلب در فریم ثابت بدنه ثابته داریم
$\left(\frac{d\boldsymbol L}{dt}\right)_\text{body roham-fixed} = \frac{d(\mathbf I \boldsymbol \omega)}{dt} = \mathbf I \frac{d\boldsymbol\omega}{dt}\tag{roham3}$
ترکیب معادلات (1)، (2) و (3) نتیجه میده
$\mathbf I \frac{d\boldsymbol\omega}{dt} = \sum_i \boldsymbol \tau_{\text{ext},i} - \boldsymbol \omega\times(\mathbf I \times \boldsymbol \omega)\tag{4}$
این معادلات حرکت اویلر برای یک جسم صلبه. با این حال عبارت$-\boldsymbol \omega\times(\mathbf I \times \boldsymbol \omega)$
در اصل یک گشتاور اینرسیه. همانطور که نیروهای اینرسی در فریم های اینرسی ناپدید میشن این گشتاور اینرسی نیز ناپدید میشه
نیروی اویلر برای آونگ
من یک سوال در رابطه با نیروی اویلر دارم. چرا این نیرو هرگز برای یک آونگ ساده در نظر گرفته نمیشود؟
تا آنجا که من متوجه شدم نیروی اویلر با (فرض کنید آونگ 2 بعدی را در یک فضای سه بعدی در نظر بگیرم که کمیت ها بردار هستن) داده میشود.
$\begin{equation}
\boldsymbol{\dot{\omega}} \times \mathbf{r}
\end{equation}$این به معنای ناپدید شدن نیرو $\boldsymbol{\dot{\omega}} = 0$ است
، یا r=0 ، یا بردارها باید در یک جهت باشند. من نمی دانم چرا یکی از این شرایط برآورده شده .این یک شبه نیروی اینرسیه که وقتی در یک چارچوب غیر گالیله ای قرار داره ایجاد میشود. ω سپس سرعت شعاعی فریم مرجع شما نسبت به یک فریم گالیلیه. اینجا اینطور نیست.
اگر ناظری در انتهای آونگ خود بزارم تجربیات انجام شده در آن باید آن را در نظر بگیرم
درباره $\frac{d L}{d t}=\tau$ در یک مرکز چرخشی فریم جرمی
رهام با جرم M روی واگن راه آهنی ایستاده که یک پیچ بدون کرانه به شعاع R را با سرعت v می‌چرخونه. من رو به جهت حرکته
گشتاور مرکز جرم برابره $-N_{1} \frac{d}{2}+N_{2} \frac{d}{2}+\left(f_{1}+f_{2}\right) L=0$
سوالم $-N_{1} \frac{d}{2}+N_{2} \frac{d}{2}+\left(f_{1}+f_{2}\right)L=0$
معادله فوق از مرکز جرم رهام به عنوان نقطه ای استفاده میکنه که معادله $\frac{d L}{d t}=\tau$ استفاده شده
این معادله در یک فریم اینرسی درسته اما مرکز جرم چرخان و در نتیجه غیر اینرسیه پس چگونه معادله صحیح است؟این معادله در یک فریم اینرسی درسته اما مرکز جرم چرخان و در نتیجه غیر اینرسیه پس چگونه معادله صحیح است؟
مرکز جرم به خودی خود فقط یک نقطیه هیچ فریم منحصر به فردی به مرکز جرم متصل نیست. معمولا وقتی میگیم فریم COM هیچ چرخشی وجود نداره و فریمی را می گیریم که در همه زمان ها مرکز جرم آن در مبدأ باشه
اساساً وقتی نیروی خالص صفره محاسبه گشتاور در مورد هر نقطه از فضا باید مطابقت داشته باشه. بنابراین یک فریم اینرسی بگیرم و گشتاورهای مربوط به COM را محاسبه کنم من میتونم گشتاور را با توجه به هر نقطه داده شده در هر سیستم مختصات معین محاسبه کنم. به طور خاص می تواید گشتاور را نسبت به مرکز جرم با تمام بردارهای نمایش داده شده در سیستم مختصات اینرسی محاسبه کنم. فقط به این دلیل که نقطه ای را برای محاسبه گشتاور با توجه به آن انتخاب میکنم به این معنی نیست که باید سیستم مختصات را تغییر بدم و آن را به آن نقطه منتقل کنم. فقط باید حاصل ضربات بردارهایی را بگیرم که از نقطه انتخاب شده به نقاطی که در آن نیروهای مختلف اعمال میشه اشاره کرده و آنها را با هم جمع کنم معادله دیفرانسیل که من اشاره کردم به یک سیستم مختصات اینرسی نیاز داره. در یک غیر اینرسی من فقط باید آن را با گشتاورهای ساختگی مربوطه اصلاح کنم تا چیزی شبیه به این $\text{Inertial: } \frac{d \vec{L}}{dt} \, = \, \vec{\tau}$
$\text{Non-inertial: } \frac{d \vec{L}}{dt} \, = \, \vec{\tau} \, + \, \vec{\tau}_{\text{fict}}$
به عنوان مثال، در دینامیک جسم صلب در یک فریم اینرسی من دارم
$\frac{d \vec{L} }{dt} \, = \, \vec{\tau}$اما در فریم محکم به جسم وصل شده و در مرکز جرم قرار داره
$\frac{d \vec{L}}{ dt} \, = \, \vec{\tau} \, + \, \vec{L} \times \vec{\omega}$جایی که $\vec{\omega}$
سرعت زاویه ای است که در فریم ثابت جسم بیان میشه. $\vec{L}$
و $\vec{\tau}$ همچنین در فریم ثابت بدن بیان میشن
من یک گاری دارم که بالای آن رهام خودم ثابتم که به طور یکنواخت در امتداد دایره ای به شعاع R حرکت میکنم با سرعت ثابت مقدار v اجازه بدین یک سیستم مختصات اینرسی را ثابت کنم در مرکز قوس دایره ای تشکیل شده توسط ریل قطار، x و y محورهای مختصات هم تراز با زمین و z محور عمود بر آن $\vec{r} \, = \, \vec{r}(t)$ بردار باشه که از مبدأ سیستم به نمایان شدن مرکز جرمم روی گاری اشاره میکنه (گاری از مسیرهای قطار دایره ای در x,y پیروی میکنه
صفحه افقی). سپس چون گاری به طور یکنواخت در امتداد یک دایره $\frac{d^2\vec{r}}{dt^2} \, = \, - \frac{v^2}{R^2} \vec{r}$
سرعت زاویه ای گاری در سیستم اینرسیه $\vec{\omega} \, = \, \frac{v}{R} \, \vec{e}_z$از آنجایی که من نسبت به گاری بی حرکتم یعنی همان طور که گاری حرکت میکنه، سرعت زاویه ایم نسبت به سیستم اینرسی برابر با سرعت زاویه ای گاری ω هستش در نتیجه، تکانه زاویه ای رهام در سیستم مختصات اینرسی به نظر میرسه
$\vec{L} \, = \, I \,\vec{\omega}\,= \, I_{z} \, \frac{v}{R} \, \vec{e}_z$جایی که$I_z$
ممان اینرسی رهامه که در امتداد محور عمودی که از مرکز جرمم می گذره محاسبه میشه که همیشه با z موازیه.
محور سیستم مختصات اینرسی بنابراین $I_z$ ثابت است این پیکربندی خاص خاصه. اگر من به نحوی کج شده بودم به طوری که محورهای اینرسیم مانند دیاگرام FBD نبود آنگاه معادله به یک جمله اضافی برای یک تکانه زاویه ای در حال تغییر زمان نیاز داشت. اما به دلیل نحوه ایستادن رهام روی گاری تکانه زاویه ای و سرعت زاویه ای در یک راستا قرار میگیرند . این به این دلیله که یک محور اینرسی مرد با z- ترازه
محور مختصات سیستم مختصات اینرسی در حالی که دو محور اینرسی دیگر همیشه به موازات x،y- میچرخند.صفحه مختصات سیستم مختصات اینرسی.
نیروهایی که در سیستم مختصات اینرسی بر روی رهام روی گاری وارد میشن هستند
$N_1 \vec{e}_z, \,\,\, N_2 \vec{e}_z, \,\,\, - \, \frac{f_1}{R}\vec{r}, \,\,\, - \, \frac{f_2}{R}\vec{r}, \,\,\, -\,\vec{mg}\,\vec{e}_z$
بردار $\vec{r}_G$ از مبدأ سیستم مختصات تا مرکز جرم منه $\vec{r}_G \, = \, \vec{r} \, + \, L \, \vec{e}_z$
بردارها از مبدأ دستگاه مختصات تا پایم هستند
$\vec{r}_1 \, =\, \left(1 + \frac{d}{2R}\right)\vec{r}$
$\vec{r}_2 \, =\, \left(1 - \frac{d}{2R}\right)\vec{r}$
زیرا$|\vec{r}| = R$ و بنابراین $\frac{\vec{r}}{R}$
یک بردار واحد است که با $\vec{r}$تراز شده
در همه زمان ها t.و$\vec{r}_i \, = \, \vec{r} \,\pm\, \frac{d}{2} \, \frac{\vec{r}}{R}$
بنابراین بردارها از مرکز جرم انسان تا پاهای او هستند
$\vec{r}_1 - \vec{r}_G \, = \,\,\, \left(1 + \frac{d}{2R}\right)\vec{r} \, - \, \vec{r} \, - \, L \, \vec{e}_z \, = \, \frac{d}{2R}\,\vec{r} \, - \, L \, \vec{e}_z$
$\vec{r}_2 - \vec{r}_G \, = \, \left(1 - \frac{d}{2R}\right)\vec{r} \, - \, \vec{r} \, - \, L \, \vec{e}_z \, = \, -\, \frac{d}{2R}\,\vec{r} \, - \, L \, \vec{e}_z$
حالا بیایید گشتاورها را محاسبه کنم
$(\vec{r}_1 - \vec{r}_G) \times ( \,N_1\,\vec{e}_z \,) \, = \, \frac{N_1d}{2R} \,\vec{r} \times \vec{e}_z$
$(\vec{r}_2 - \vec{r}_G) \times ( \,N_2\,\vec{e}_z \,) \, = \, - \, \frac{N_2d}{2R} \,\vec{r} \times \vec{e}_z$
$(\vec{r}_1 - \vec{r}_G) \times \left( \, - \, \frac{f_1}{R}\vec{r} \,\right) \, = \, \frac{f_1L}{R} \,\vec{e}_z \times \vec{r}$
$(\vec{r}_2 - \vec{r}_G) \times \left( \, - \, \frac{f_2}{R}\vec{r} \,\right) \, = \, \frac{f_2L}{R} \,\vec{e}_z \times \vec{r}$
گشتاور ثقل نسبت به مرکز جرم صفر است.
بنابراین معادله برداری حرکت برای تکانه زاویه ای / سرعت زاویه ایه
$\frac{d}{dt} \vec{L} \, = \,\frac{d}{dt}\left( I_{z} \, \frac{v}{R} \, \vec{e}_z\right) \,= \, \frac{N_1d}{2R} \,\vec{r} \times \vec{e}_z \, - \, \frac{N_2d}{2R} \,\vec{r} \times \vec{e}_z \,+\,\frac{f_1L}{R} \,\vec{e}_z \times \vec{r} \, +\, \frac{f_2L}{R} \,\vec{e}_z \times \vec{r}$
با این حال از آنجایی که $\frac{v}{R}$ ثابته
$\frac{d}{dt}\left( I_{z} \, \frac{v^2}{R} \, \vec{e}_z\right) \,= \, 0 \, = \, \left(\,- \, \frac{N_1d}{2R} \, + \, \frac{N_2d}{2R} \,+\,\frac{f_1L}{R} \, +\, \frac{f_2L}{R} \,\right) \, \vec{e}_z \times \vec{r}$ که میده
$- \, \frac{N_1d}{2R} \, + \, \frac{N_2d}{2R} \,+\,\frac{f_1L}{R} \, +\, \frac{f_2L}{R} \, = \, 0$و اگر هر دو طرف هویت دوم را در R ضرب کنم
، دقیقاً دریافت میکنم
$- \, \frac{N_1d}{2} \, + \, \frac{N_2d}{2} \,+\, ({f_1} \, +\, {f_2})\,L \, = \, 0$
بنابراین حدس میزنم دلیلی داره اگر حرکت در امتداد دایره یا حرکت کلی تر گاری شتاب میگرفت کل گشتاور صفر نمیشد. تنها دلیلی که معادله دوم برقراره اینه که سرعت زاویه ای و تکانه زاویه ای بردارهای ثابتی برای این حرکت یکنواخت خاص در طول یک دایره هستند!
بگذارید موقعیت مبدا $\mathbf{r}_{0}$ باشه
و اجازه دهید موقعیت ذرات $\mathbf{r}_{i}$ باشه. بردارهای $\mathbf{r}_{0}$
و$\mathbf{r}_{i}$ با توجه به یک سیستم مختصات ثابت معین اندازه گیری می شوند. تکانه زاویه ای کل سیستم، نسبت به مبدا (احتمالاً شتاب دهنده) $\mathbf{r}_{0}$
، است
$\mathbf{L}=\sum_{i}\left(\mathbf{r}_{i}-\mathbf{r}_{0}\right) \times m_{i}\left(\dot{\mathbf{r}}_{i}-\dot{\mathbf{r}}_{0}\right)$از این رو،
$\begin{aligned}
\frac{d \mathbf{L}}{d t} &=\frac{d}{d t}\left(\sum_{i}\left(\mathbf{r}_{i}-\mathbf{r}_{0}\right) \times m_{i}\left(\dot{\mathbf{r}_{i}}-\dot{\mathbf{r}}_{0}\right)\right) \\
&=\sum_{i}\left(\dot{\mathbf{r}}_{i}-\dot{\mathbf{r}}_{0}\right) \times m_{i}\left(\dot{\mathbf{r}_{i}}-\dot{\mathbf{r}}_{0}\right)+\sum_{i}\left(\mathbf{r}_{i}-\mathbf{r}_{0}\right) \times m_{i}\left(\ddot{\mathbf{r}_{i}}-\ddot{\mathbf{r}}_{0}\right) \\
&=0+\sum_{i}\left(\mathbf{r}_{i}-\mathbf{r}_{0}\right) \times\left(\mathbf{F}_{i}^{\mathrm{ext}}+\mathbf{F}_{i}^{\mathrm{int}}-m_{i} \ddot{\mathbf{r}}_{0}\right)
\end{aligned}$چون$m_{i} \ddot{\mathbf{r}}_{i}$
نیروی خالص است (یعنی $\mathbf{F}_{i}^{\text {ext }}+\mathbf{F}_{i}^{\text {int }}$
) عمل بر روی i ذره ام $\mathbf{F}_{i}^{\mathrm{int}}$ است
ناپدید میشه (همانطور که باید بررسی کنم). و چون $\sum m_{i} \mathbf{r}_{i}=M \mathbf{R}$
(که در آن $M=\sum m_{i}$ جرم کل است و R موقعیت مرکز جرم است)، داریم
$\frac{d \mathbf{L}}{d t}=\left(\sum_{i}\left(\mathbf{r}_{i}-\mathbf{r}_{0}\right) \times \mathbf{F}_{i}^{\mathrm{ext}}\right)-M\left(\mathbf{R}-\mathbf{r}_{0}\right) \times \ddot{\mathbf{r}}_{0}$اولین عبارت در اینجا گشتاور خارجی است که نسبت به مبدا $\mathbf{r}_{0}$ اندازه گیری میشود
. اگر هر یک از سه شرط زیر برآورده شود ناپدید میشه
$\mathbf{R}=\mathbf{r}_{0}$
، یعنی مبدا CM است.$\vec{r}_{0}=0$یعنی مبدأ شتاب نداره
$\left(\mathbf{R}-\mathbf{r}_{0}\right.$
) موازی $\ddot{\mathbf{r}}_{0}$ است. این شرایط به ندرت مورد استناد قرار میگیره
اگر هر یک از این شرایط برآورده شد من میتونم بنویسم
$\frac{d \mathbf{L}}{d t}=\sum\left(\mathbf{r}_{i}-\mathbf{r}_{0}\right) \times \mathbf{F}_{i}^{\mathrm{ext}} \equiv \sum_{i} \tau_{i}^{\mathrm{ext}}$
در این مسئله من چارچوب مرجع را در مرکز جرم دارم از این رو حالت 1 اعمال میشه و میتونم$\frac{d L}{d t}=\tau$بنویسم.
در مورد مرکز جرم از آنجایی که$\frac{d L}{d t}$ در فریم COM صفره و به معادله مورد نیاز $\tau$ =0 میرسم
