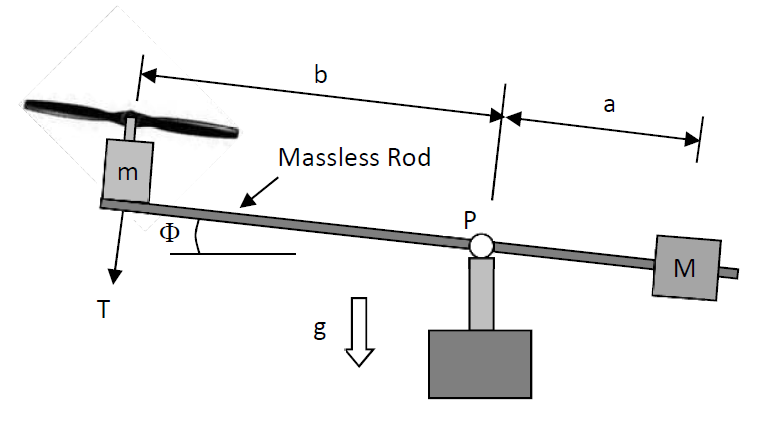
مقاومت آرمیچر موتور R، اندوکتانس L و ثابت موتور K و گشتاور واکنش روی شفت موتور$\tau$ است. T برابر $k_1w_2^2$ و $\tau$ برابر $k_2w_2^2$است.
$w_1 = \dot{\varphi}_1$
$w_2=\dot{\theta}$
معادله دیفرانسیل جریان به صورت زیر است:
$\frac{\partial I}{\partial t}=\frac{E - RI - K_1w_2}{L}$
که در آن E ولتاژ آرمیچر ورودی و معادله گشتاور است
$\frac{\partial w_2}{\partial t}=\frac{KI - K_2w_2^2}{J}$
که در آن $k_2w_2^2$گشتاور بار است و در نهایت برای آخرین معادله از روش لاگرانژ برای استخراج معادله حرکت جرم m و M استفاده کردم.$T = \frac{1}{2}mb^2\dot{\varphi}^2 + \frac{1}{2}M\alpha^2\dot{\varphi}^2 + \frac{1}{2}Jw_2^2$
$U = mgb\sin\varphi - Μg\alpha\sin\varphi$
که در نهایت می دهد$mb^2\dot{w} + M\alpha^2\dot{w}_1 + bmg\cos\varphi - Mg\alpha\cos\varphi = -Tb = K_1w_2^2b$
$\frac{\partial w_1}{\partial t} = \frac{-k_1w_1^2 + Mg\alpha\cos\varphi - mgb\cos\varphi}{M\alpha^2 + mb^2}$
من می خواهم بدانم که آیا همه چیز در اینجا درست است و چگونه می توان آن را حول φ=0 خطی کرد، زیرا وقتی سعی می کنم انجام دهم که $\dfrac{\partial w_1}{\partial t}$ تبدیل به یک ثابت می شود که عبارت است از:
$\frac{\partial w_1}{\partial t} = \frac{Mg\alpha - mgb}{M\alpha^2 + mb^2}$
لاگرانژی برای سیستم گام 1 بعدی شما L:=T−U است که این است
$\mathcal{L} = \frac{1}{2}(mb^2 + Ma^2)\dot{\phi}^2 + \frac{1}{2}J\dot{\theta}^2 + (Ma - mb)g\sin\phi$
معادلات اویلر-لاگرانژ هستند$\frac{d}{dt}\bigg(\frac{\partial\mathcal{L}}{\partial \dot{q}_k}\bigg) + \frac{\partial\mathcal{L}}{\partial q_k} = Q_k$
این به EOM می دهد$(mb^2 + Ma^2)\ddot{\phi} + (Ma - mb)g\cos\phi = -Tb = -k_1\dot{\theta}^2b$
تحت یک تقریب زاویه کوچک، cosφ≈1، بنابراین این حالت $(mb^2 + Ma^2)\ddot{\phi} + (Ma - mb)g = -k_1b\dot{\theta}^2,$
یا به شکل دیگری،
$\ddot{\phi} = \frac{mb-Ma}{mb^2 + Ma^2}g - \frac{k_1b}{mb^2 + Ma^2}\dot{\theta}^2 = \beta_1 - \beta_2\dot{\theta}^2.$.
حالا، من نمیدانم که آیا این معادلات برای سیستم شما درست است یا نه، اما بر اساس آنچه در سؤال خود بیان کردید، این همان چیزی است که EOM برای ϕ(t) است.
شما همچنین یک سیستم جفت شده از ODE برای I(t) و θ(t) دارید زیرا از θ˙=ω2 نتیجه می شود که
$\begin{align}
\ddot{\theta} &= \frac{K}{J}I - \frac{k_2}{J}\dot{\theta}^2\\
\dot{I} &= \frac{E}{L} - \frac{R}{L}I - \frac{k_1}{L}\dot{\theta}
\end{align}$
باز هم، همه اینها بر اساس مدل شما است که در بیانیه مشکل نوشتید. بنابراین، در مجموع، شما سه ODE برای سه متغیر θ,φ,I دارید. با توجه به اینکه این سیستم از 3 ODE غیرخطی است، هیچ راه حل تحلیلی وجود ندارد. کاری که می توانید برای شبیه سازی این موضوع انجام دهید حل سیستم در متلب است، به عنوان مثال با استفاده از ODE45 یا هر حلگر معادله دیفرانسیل.
اگر می خواهید این سیستم را خطی کنید، می توانید موارد زیر را انجام دهید. ابتدا سیستم را به شکل فضای حالت قرار دهید، یعنی اجازه دهید$x = [\phi,\dot{\phi},\theta,\dot{\theta},I]^\intercal$ به طوری که دینامیک کامل باشد.
$\begin{align}
\dot{x}_1 &= x_2\\
\dot{x}_2 &= \beta_1\cos x_1 - \beta_2 x_4^2\\
\dot{x}_3 &= x_4\\
\dot{x}_4 &= \frac{K}{J}x_5 - \frac{k_2}{J}x_4^2\\
\dot{x}_6 &= \frac{E}{L} - \frac{R}{L}x_5 - \frac{k_1}{L}x_4.
\end{align}$
توجه کنید که معادلات غیر خطی دوم و چهارم هستند. بنابراین در حال حاضر سیستمی مانند x˙=f(x)، که در آن f(x) یک تابع غیرخطی (بردار 5 در 1) است. برای خطی کردن این سیستم به شکل x˙=Ax، می توانید تنظیم کنید
$A = \bigg[\frac{\partial f}{\partial x}\bigg]_0,$
در برخی شرایط اسمی ارزیابی می شود که یک ماتریس 5 در 5 به دست می دهد. در مورد شما این می دهد
$A =
\begin{bmatrix}
0 & 1 & 0 & 0 & 0\\
-\beta_1\sin x_1 & 0 & 0 & -2\beta_2 x_4 & 0\\
0 & 0 & 0 & 1 & 0\\
0 & 0 & 0 & -2\frac{k_2}{J}x_4 & \frac{K}{J}\\
0 & 0 & 0 & -\frac{k_1}{L} & -\frac{R}{L}
\end{bmatrix}_0$
بنابراین باید یک نقطه مرجع برای خطی سازی ϕ و θ˙ پیدا کنید و سپس می توانید سیستم خطی شده را شبیه سازی کنید.hope I helped you understand the question. Roham Hesami, sixth
semester of aerospace engineering



