روش اول
رانش برابر است با سرعت جریان جرمی ضربدر سرعت اگزوز.$F=\dot{m}v$
نرخ جریان جرمی با استفاده از چگالی آب، ناحیه نازل و سرعت خروجی اگزوز یافت می شود.$\dot{m}=\rho A v$
با ترکیب به دست می آوریم
$F=\rho A v^2$مجذور سرعت اگزوز برابر با 2 برابر فشار گیج داخلی تقسیم بر چگالی آب است.
$v^2=2P/\rho$
با ترکیب می بینیم که رانش برابر با 2 برابر سطح نازل ضربدر فشار است.$F=2AP$
روش دوم
در تصویر زیر به نظر می رسد که رانش بر روی موشک باید برابر با عدم تعادل نیرو باشد که توسط فلش ها نشان داده شده است. این عدم تعادل نیرو، برابر فشار گیج داخلی ضربدر ناحیه نازل است.
$F=AP$
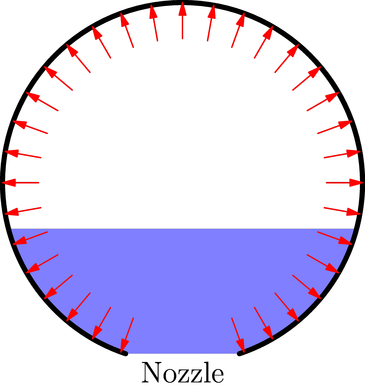
من فکر می کنم شکل زیر نمایش بهتری از نیروی رانش است. فشار داخلی (فلش های قرمز) در نزدیکی دهانه نازل کاهش می یابد زیرا سرعت جریان آب قابل توجه است. همچنین، فشار آب در دهانه نازل همانطور که در ابتدا تصور میکردم، در فشار صفر نیست. در عوض، فشار دینامیکی (فلش های سبز) وجود دارد که با سرعت جریان نسبت معکوس دارد. عدم تعادل نیرو برابر است با دو برابر فشار هوا در ناحیه نازل$، F=2AP.$
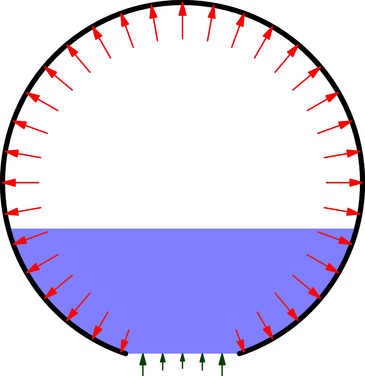
افت فشار از فشار مخزن به فشار اتمسفر فوراً در نازل رخ نمی دهد، بلکه بر اساس مساحت کانال جریان پخش می شود. این فشار کاهش یافته منجر به رانش اضافی می شود که در راه حل دوم شما در نظر گرفته نشده است. در اینجا یک راه برای محاسبه این تراست گمشده اضافی وجود دارد:
روش اول صحیح است. در مرحله دوم، شما فرض کرده اید که فشار در نازل با وجود خروج آب با سرعت کمی، همچنان P است. یعنی فشار دینامیکی را نادیده گرفته اید.
شما باید از اصل برنولی استفاده کنید
$P + \frac{\rho v^2}{2} + \rho h g = {\rm constant}$
روش اول شما فرض می کند که سطح بالایی آب به سختی حرکت می کند (زیرا مساحت سطح آن بسیار بزرگتر از ناحیه نازل است). با اعمال همین ایده برای روش دوم، می توانیم ثابت را هم در آب و هم بلافاصله زیر نازل به صورت محاسبه کنیم.
$P = P_A + \frac{\rho v^2}{2},$
که در آن $P_A$ فشار اتمسفر است و ما از عبارت$ ρhg$ کوچک غفلت می کنیم که فشار را به دلیل ستون مایع بالای نازل در LHS افزایش می دهد. اگر بیشتر فرض کنیم که$P \gg P_A$آنگاه$P = \rho v^2/2$و نرخ تغییر تکانه مایع از نازل برابر است.
$F = \rho A v^2 = 2PA$
افت فشار از فشار مخزن به فشار اتمسفر فوراً در نازل رخ نمی دهد، بلکه بر اساس مساحت کانال جریان پخش می شود. این کاهش فشار منجر به رانش اضافی می شود که در راه حل دوم شما در نظر گرفته نشده است. در اینجا یک راه برای محاسبه این تراست گمشده اضافی وجود دارد:
معادله برنولی (معادله دوم تا آخرین شما) اعمال می شود:
$P + \frac{\rho v^2}{2} + \rho h g = {\rm constant}$
ما می توانیم این را با معادله جریان جرمی ترکیب کنیم تا به دست آوریم:
$P+\frac12\rho \left(\frac{\dot m}{\rho A}\right)^2 = constant$
پاسخاصلی شما سرعت ناچیز/منطقه بزرگ در سطح آب را فرض میکند:
$P_{tank} + 0 = constant$این ثابت ما را به ما می دهد:
$P+\frac12\rho \left(\frac{\dot m}{\rho A}\right)^2 = P_{tank}$
و ما می دانیم که فشار در خروجی اتمسفر / فشار 0 گیج است:
$0 + \frac12\rho \left(\frac{\dot m}{\rho A_{exit}}\right)^2 = P_{tank}$
ما می توانیم برای $\dot m$ حل کنیم:
$\dot m = A_{exit}\sqrt{2 \rho P_{tank}}$
اتصال مجدد
$P+P_{tank}\left(\frac{A_{exit}}{A}\right)^2 = P_{tank}$
حل فشار:$P = P_{tank} \left(1-\left(\frac{A_{exit}}{A}\right)^2\right)$
بنابراین اگر بخواهیم نیروی رانش اضافی را به دلیل پایین بودن فشار در نزدیکی نازل محاسبه کنیم، باید فشار را با ناحیه یکپارچه کنیم:
$F = F_{up} - F_{down} = \int_{A_{exit}}^\infty \left (P_{tank} - P_{tank} \left(1-\left(\frac{A_{exit}}{A}\right)^2\right) \right) \; dA$
$F = P_{tank} \int_{A_{exit}}^\infty \frac{{A_{exit}}^2}{A^2} \; dA$
$F = P_{tank} A_{exit}$
بنابراین PA گم شده از راه حل دوم شما وجود دارد.
1: می توانید معادلات خود را دقیق تر کنید (مخصوصاً برای موشک های بطری نازک) با استفاده از سطح مقطع واقعی در سطح آب به جای بی نهایت، هم در اینجا و هم در حد انتگرال.helped you understand the question. Roham Hesami, sixth
semester of aerospace engineering



