این سیستم مطابق تصویر زیر ساخته شده است (فقط یک طرح):
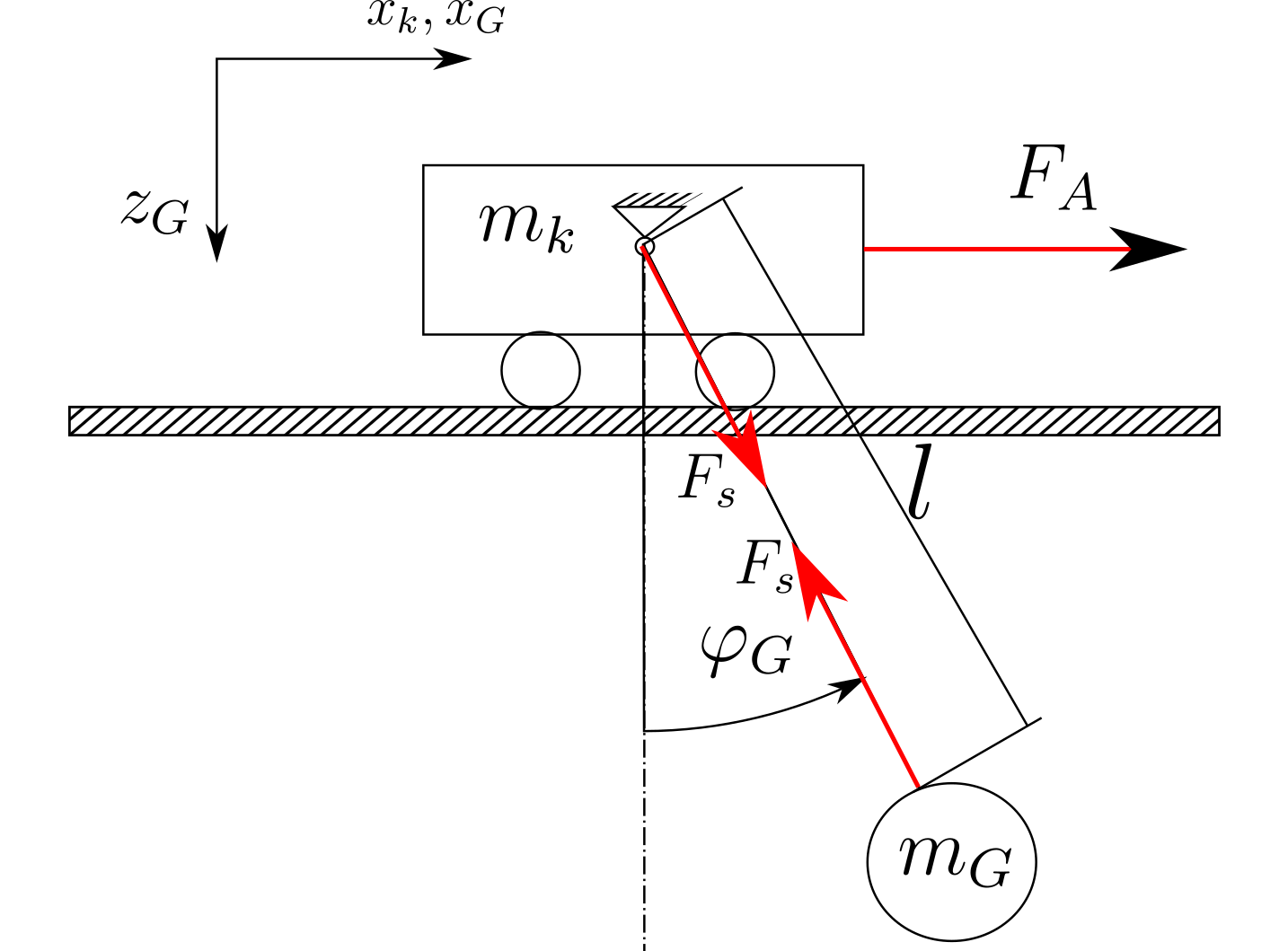
اگر از روش نیوتن استفاده کنم، با نادیده گرفتن اصطکاک، مقاومت هوا و تغییرات طول طناب، معادلات زیر را به دست می‌آورم:
$m_k \ddot{x}_{k} = F_{A} + F_{S} \sin(\varphi) \\
m_G \ddot{x}_{G} = -F_{S} \sin(\varphi) \\
m_G \ddot{z}_{G} = m_{G} g - F_{S} \cos(\varphi)$وقتی به روابط سینماتیکی از گیره نگاه می کنم (دایره با وزن mG
) معادلات زیر را بدست می آورم.
$x_{G} = x_{k} + l \sin(\varphi) \\
z_{G} = l \cos(\varphi)\\
\varphi = \omega t = \dot{\varphi} t$اوزن mk را می شناسم
و mG و طول l اما ارزش ها در حال حاضر مهم نیستند.
هدف این است که در پایان دو معادله دیفرانسیل داشته باشیم. یک معادله باید رابطه بین نیروی محرکه FA را نشان دهد
و مسیر چرخ دستی xk (با مشتقات) معادله دیگر باید رابطه بین نیروی محرکه FA را نشان دهد
و زاویه طناب $\varphi_G$
بعد از آن من می خواهم توابع انتقال (تبدیل لاپلاس و غیره) را انجام دهم اما مشکل این نیست.
مشکل این است که به نظر نمی رسد آن معادلات را پیدا کنم. بهترین رویکرد من تا کنون به این صورت است:
$m_{k} \ddot{x}_{k} = F_{A} + F_{S} \sin(\varphi)$پس این بدان معناست که اگر
$m_G \ddot{x}_{G} = -F_{S} \sin(\varphi) \\
F_{S} \sin(\varphi) = -m_{G} \ddot{x}_{G} \\$می توانم بگویم:
$m_{k} \ddot{x}_{k} = F_{A} - m_{G} \ddot{x}_{G} \\$و اگر xG را استخراج کنم
مثل این:
$x_{G} = x_{k} + l \sin(\varphi) \\
\dot{x}_{G} = \dot{x}_{k} + l \dot{\varphi} \cos(\varphi) \\
\ddot{x}_{G} = \ddot{x}_{k} + l \left[ \ddot{\varphi} \cos(\varphi) - \dot{\varphi}^{2} \sin(\varphi) \right]$من در واقع اینجا گیر کردم زیرا نمی توانم راهی برای حذف φ پیدا کنم
از معادلات قضایای جمع اصلاً به من کمک نمی کند (یا من از آنها به درستی استفاده می کنم).
آیا کسی ایده ای دارد که چگونه باید در این مرحله ادامه دهم؟ امیدوارم نیازی به راه حل کامل نداشته باشم. من در واقع بیشتر به انجام این کار علاقه دارم و امیدوارم که به سمت مسیر درست حرکت کنم.
حدس من این است که شما احتمالاً به معادله دیفرانسیل دیگری برای حرکت زاویه ای نیاز دارم که شامل اینرسی باشد، مانند:
$m_G l^2 \ddot{\varphi} = m_G g l \sin(\varphi)$که حاصل میشه
$\ddot{\varphi} = \frac{g}{l} \sin(\varphi)$سپس می توانم از تقریب زوایای کوچک استفاده کنم
$\sin(\varphi) \simeq \varphi$مثال آونگ معکوس را بررسی کنید.
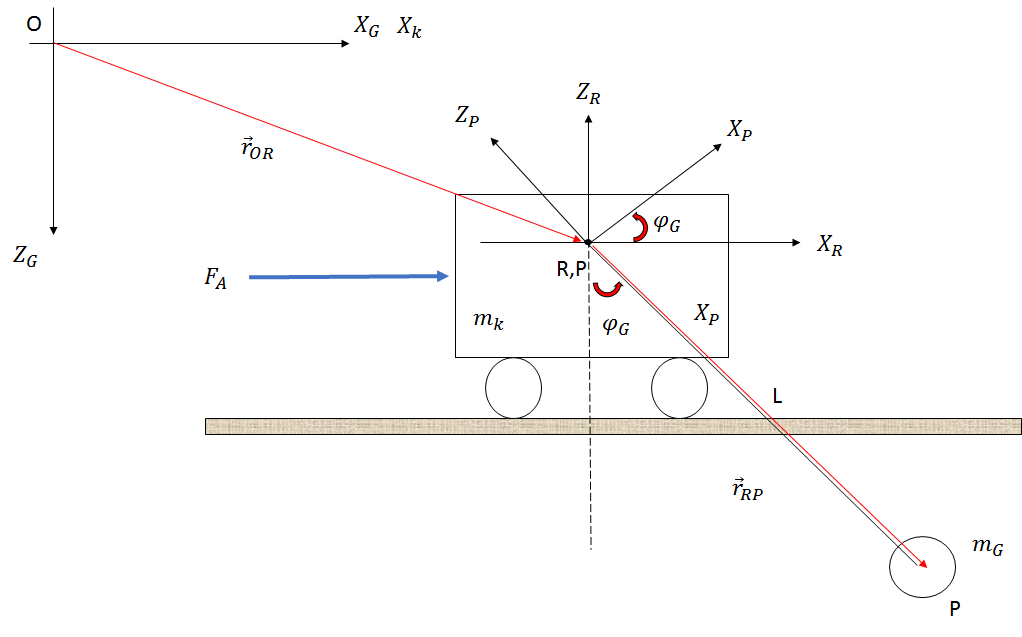اینها مراحل حل مشکلاتی از این قبیلهسینماتیک سیستم را تحلیل کنید.
$_{o}\vec{r}_{RP}$
$_{o}\vec{r}_{OP}$
$\big(x_{k}î + 0j + 0k \big)$
$\big[\big(x_{k}+\sin(\varphi)l\big)î + 0j + \big(\cos(\varphi)l\big)k\big]$
توجه: $R(\varphi)$
یک ماتریس چرخشی است و$x_{G} = x_{k}+\sin(\varphi)l$
.در نظر گرفتن مشتقات زمانی:
$\dot{x_{k}}+\cos(\varphi)\dot{\varphi}l$
$\ddot{x_{k}} + l\cos(\varphi)\ddot{\varphi} - l\sin(\varphi)\dot{\varphi}^{2}$
از معادله نیوتن استفاده کنید:$m_{k}\ddot{x_{k}} = F_{A} - m_{G}\ddot{x_{G}}$
$x_{G}$ را جایگزین کنم
$m_{k}\ddot{x_{k}} = F_{A} - m_{G}\big(\ddot{x_{k}} + l\cos(\varphi)\ddot{\varphi} - l\sin(\varphi)\dot{\varphi}^{2}\big)$
$\big(m_{k}+m_{G}\big)\ddot{x_{k}} + m_{G}\big(l\cos(\varphi)\ddot{\varphi}\big) - m_{G}\big(l\sin(\varphi)\dot{\varphi}^{2}\big)= F_{A}$
For the z axis
$m_{G}g-l\big(\cos(\varphi)\dot{\varphi}^{2}+\sin(\varphi)\ddot{\varphi}\big)$از قانون دوم نیوتن برای چرخش استفاده کنم
$F_{Z}l\sin(\varphi)-\big(m_{G}\ddot{x_{G}}\big)l\cos(\varphi)$
$F_{Z}l\sin(\varphi) = m_{G}gl\sin(\varphi)-l^{2}\big(\cos(\varphi)\sin(\varphi)\dot{\varphi}^{2}+\sin(\varphi)^{2}\ddot{\varphi}\big)$
$\big(m_{G}\ddot{x_{G}}\big)l\cos(\varphi) = m_{G}\big(l^{2}\cos(\varphi)^{2}\ddot{\varphi}\big) - m_{G}\big(l^{2}\cos(\varphi)\sin(\varphi)\dot{\varphi}^{2}\big)+m_{G}\ddot{x_{K}}l\cos(\varphi)$استفاده از توابع مثلثاتی:
$m_{G}gl\sin(\varphi)-m_{k}l\cos(\varphi)\ddot{x_{k}}$
