Free vibrations in immortal systems
ارتعاش آزاد به این معنی است که هیچ نیروی خارجی متغیر زمانی روی سیستم وارد نمی شود. یک سیستم یک درجه آزادی دارد اگر بتوان حرکت آن را به طور کامل توسط یک متغیر اسکالر توصیف کرد.برخی از نمونههای ارتعاشات آزاد عبارتند از: نوسان آونگ ساده، نوسانات جسم متصل به فنر افقی، صدای تولید شده توسط چنگال کوک در فاصله کوتاه، نتهای آلات موسیقی، لوله ارگ و غیره.ارتعاش آزاد زمانی اتفاق می افتد که یک سیستم مکانیکی با یک ورودی اولیه به حرکت در می آید و اجازه می دهد آزادانه ارتعاش کند. نمونه هایی از این نوع ارتعاش عبارتند از عقب کشیدن کودک روی تاب و رها کردن آن، یا ضربه زدن به چنگال تنظیم و اجازه دادن به زنگ زدن

مطابق توضیحاتی که پستهای قبلم تا به اینجا ارائه شد، اگر نیروی $\large \overrightarrow{F} (t)$ به جرم m وارد شود و آن را در جهت نیرو و به اندازه فاصله
$\large \overrightarrow{x} (t)$ جابجا کند، قانون دوم نیوتن به صورت زیر نوشته میشود.$\large \overrightarrow{F} (t) \:= \:\frac{\text{d} }{\text{d}t} (m\frac{\text{d} \overrightarrow{x} (t)}{\text{d}t})$اگر جرم m ثابت باشد، رابطه بالا به صورت زیر در خواهد آمد.$\large \overrightarrow{F} (t) \:= \:m\frac{\text{d} ^2 \overrightarrow{x} (t)}{\text{d} t^ 2} \:= \:m\ddot{\overrightarrow{x}}$(رابطه ۱)
در رابطه بالا، $\large \ddot{\overrightarrow{x}} \:= \:\frac{\text{d} ^2 \overrightarrow{x} (t)}{\text{d} t^ 2}$
شتاب جرم را نشان میدهد. برای جسم صلبی که حرکت دورانی دارد، قانون نیوتن به صورت زیر است.$\large \overrightarrow{M} (t) \:= \:J \ddot{\overrightarrow{\theta}}$
(رابطه ۲)در رابطه ۲، $\large \overrightarrow{M}$
گشتاور اعمال شده به جسم صلب و $\large \overrightarrow{\theta}$
و $\large \ddot{\overrightarrow{\theta}} \:= \:\frac{\text{d} ^2 \theta (t)}{\text{d} t^2}$
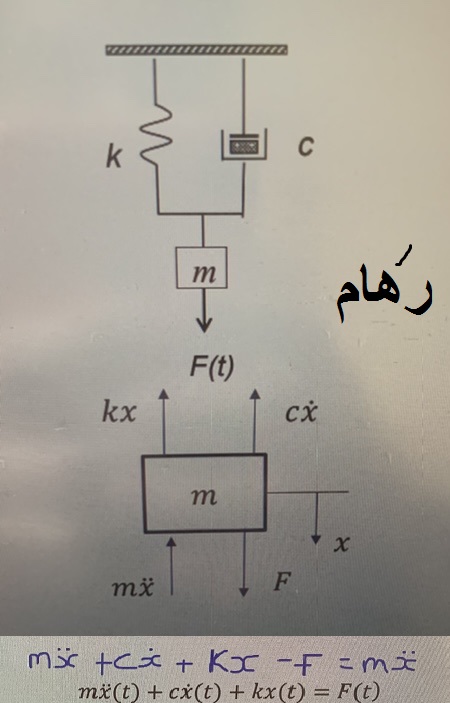
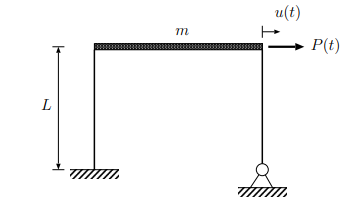
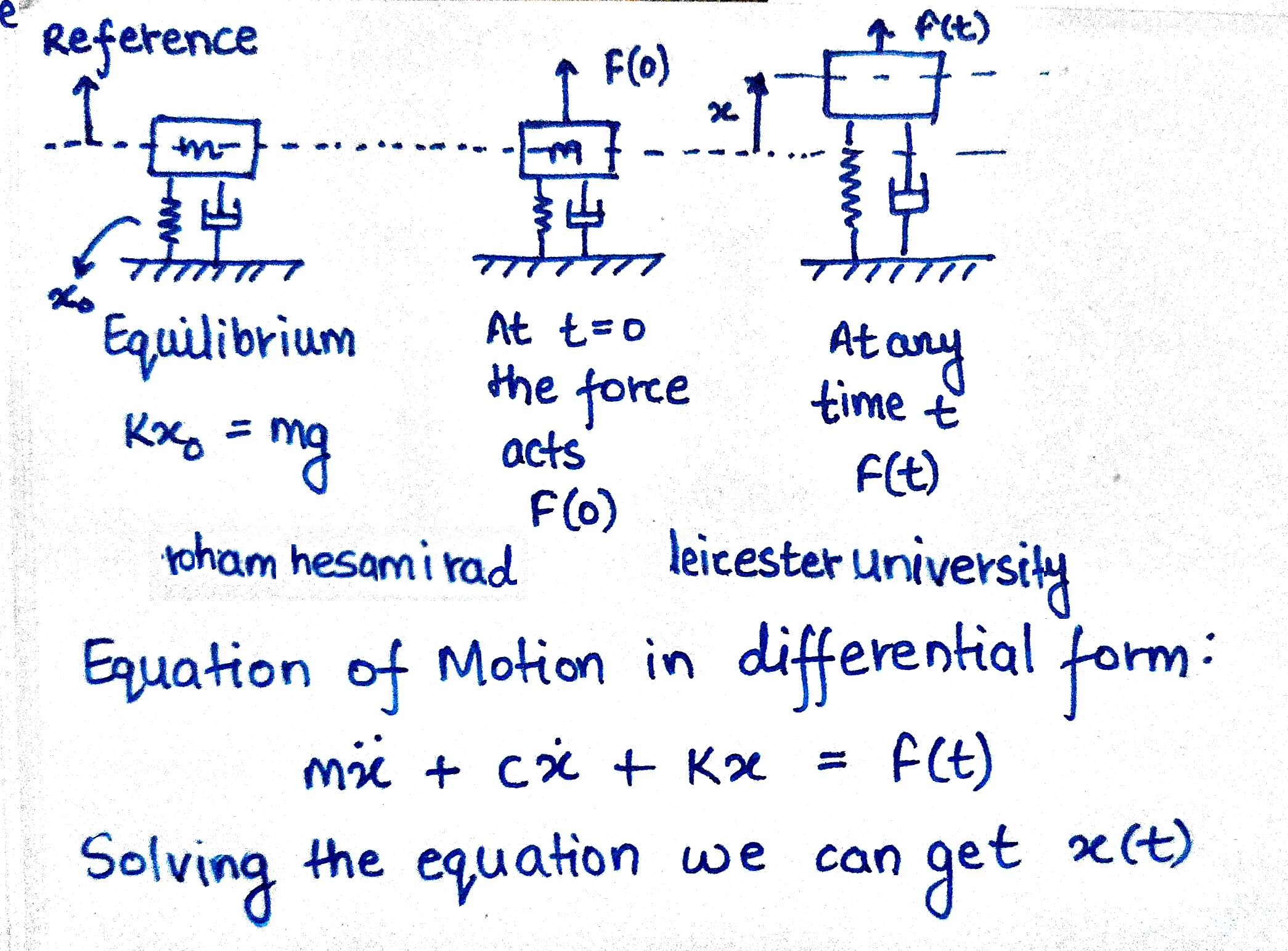
¨ نیز به ترتیب، جابجایی زاویهای و شتاب زاویهای آن هستند. رابطههای ۱ و ۲، معادلات حرکت سیستم در حالت ارتعاشات آزاد را نشان میدهند. اکنون، سیستم یک درجه آزادی و نامیرای نشان داده شده در شکل زیر را در نظر بگیرید.ارتعاشات آزاد
جرم m روی تکیهگاهی از نوع غلتکی و بدون اصطکاک است و آزادانه در جهت افقی حرکت انتقالی دارد. هنگامی که جرم نسبت به موقعیت تعادل استاتیکیاش، به اندازه
+x جابجا شود، نیروی فنر برابر kx خواهد بود. استفاده از رابطه ۱ برای این جرم، به معادله زیر منجر میشود.$\large F(t) \:= \:- kx \:= \:m\ddot{x} \\~\\
\large m\ddot{x} \:+ kx \:=0$
(رابطه ۳)برای استخراج معادله حرکت سیستمی که ارتعاشات آزاد دارد، چندین روش وجود دارد که از بین آنها میتوان به قضیه دالامبر، اصل جابجایی مجازی و قانون پایستگی انرژی اشاره کرد.
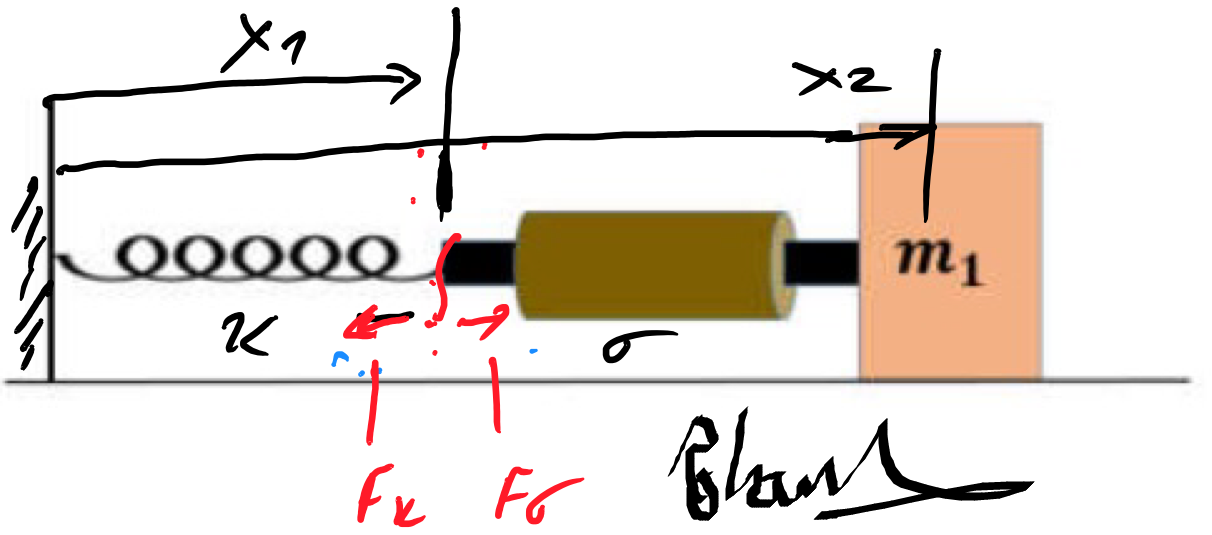
ارتعاشات آزاد سیستم جرم و فنر در جهت قائم سیستم جرم و فنر نشان داده شده در شکل زیر را در نظر بگیرید. جرم m از پایینترین نقطه فنر آویزان است. انتهای دیگر فنر را به یک تکیهگاه صلب متصل کردهایم. در حالت سکون، جرم در موقعیت تعادل استاتیکی قرار دارد.
در این حالت، نیروی گرانش وارد به جرم m ، دقیقاً با نیروی کشش فنر که از طرف جرم و به سمت بالا وارد میشود، برابر است. در نقطه تعادل استاتیکی، فنر به اندازه
$\large l_0 \:+ \:\delta _{st}$
کشیده میشود، که
$\large \delta _{st}$
برابر با جابجایی استاتیکی ناشی از وزن W است. با دقت در شکل، تعادل استاتیکی را میتوان به صورت زیر نوشت.
ارتعاشات سیستم جرم و فنر
$\large W \:= \:m g\: =\: k\delta _{st}$
حال، جرم m را نسبت به این وضعیت تعادل به اندازه +x جابجا میکنیم (شکل ب). در این حالت، نیروی کشش فنر به مقدار
$\large -\:k (x \:+ \:\delta _{st})$
میرسد. با استفاده از قانون دوم نیوتن، روابط زیر به دست میآید.$\large m\ddot{x} \:= \:-k (x\: +\:\delta _{st}) \:+ \:W \\~\\
\large k\delta _{st} \:= \:W \\~\\
\large \Rightarrow ~~~ m\ddot{x} \:+ \:kx \:= \:0$
همانطور که مشاهده میکنید نتیجه به دست آمده، مشابه رابطه ۳ است. به عبارت دیگر، هنگام بررسی ارتعاشات آزاد جرمی که در راستای قائم حرکت میکند، میتوانیم از وزن آن صرف نظر کنیم. زیرا معادلات حرکت را نسبت به تعادل استاتیکی آن سیستم مینویسیم. در ادامه به حل رابطه ۳ میپردازیم.
$\large x(t) \:= \:Ce ^{st}$
در این رابطه، C و s
ثابت هستند و مقدارشان باید مشخص شود. رابطه بالا را در رابطه شماره ۳ جایگذاری میکنیم.
$\large C( ms ^2 \:+ \:k) \:= \:0 \\~\\
\large C \:\neq \:0 \\~\\
\large \Rightarrow ms ^2 \:+ \:k \:= \:0$
(رابطه ۴)$\large s\: =\: \pm\: (-\: \frac {k} {m}) ^{1/2} \:= \:\pm \:i \omega _n \\~\\
\large i\: =\: (-\:1) ^{1/2} \\~\\
\large \Rightarrow \omega _n\: =\: (\frac {k} {m}) ^{1/2}$
رابطه ۴ را معادله مشخصه یا معادله کمکی مربوط به رابطه ۳ مینامند. دو مقدار به دست آمده برای s، ریشههای معادله مشخصه هستند که تحت عنوان مقادیر مشخصه یا مقادیر ویژه شناخته میشوند. از آنجایی که هر دو مقدار s، در رابطه ۴ صدق میکنند، پاسخ عمومی رابطه شماره ۳ را میتوان به صورت زیر نشان داد.$\large x(t) \:= \:C_1 e^ {i\omega_n t} \:+ \:C_2 e^ {-i\omega_n t}$
با استفاده از فرمول اویلر که به صورت زیر تعریف میشود، میتوانیم رابطه بالا را بازنویسی کنیم.$\large e^ {\pm i\alpha t} \:= \:\cos\alpha t\: \pm\:i \sin \alpha t\: \\~\\
\large x(t) \:= \:A _1 \cos \omega _nt \:+ \:A_2 \sin \omega _nt$
ثابتهای C1 و C2 یا ثابتهای جدید A1 و A2 را میتوان با کمک شرایط اولیه سیستم، تعیین کرد. برای مشخص شدن هر دو ثابت، دو شرط اولیه مختلف مورد نیاز است. در اینجا، اگر مقادیر جابجایی x(t)
و سرعت $\large \dot{x}(t) \:= \:(\frac{\text{d}x}{\text{d}t}) (t)$
را در لحظه t=0، به ترتیب $\large x_0$و$\large \dot{x}_0$
بنامیم، با کمک رابطه ۵ میتوانیم به نتایج زیر برسیم.$\large x(t \:= \:0) \:= \:A _1\: =\: x_0 \\~\\
\large \dot{x}(t \:= \:0) \:= \:\omega_n A_2 \:= \:\dot{x}_0$
در نتیجه، ضرایب ثابت به صورت $\large A_1 \:= \:x_0$و$\large A_2 \:= \:\dot{x}_0/ \omega_n$
به دست میآید. حال، میتوانیم رابطه ۳ را به شیوه زیر بازنویسی کنیم.$\large x(t) \:= \:x_0 \cos \omega _nt \:+ \:\frac {\dot{x} _0} {\omega _n} \sin \omega _nt$
حرکت هارمونیک در ارتعاشات آزاد
رابطه ۶، تابعی هارمونیک از زمان است و حرکت متقارنی حول موقعیت تعادل جرم
m دارد. هر دفعه که جرم از این موقعیت عبور میکند، سرعت و شتاب به ترتیب به مقدار ماکسیمم و صفر میرسند. هنگامی هم که جرم m در بیشترین دامنه قرار میگیرد، مقدار سرعت و شتاب آن به ترتیب صفر و ماکسیمم خواهد بود. به این حرکت، هارمونیک گفته میشود و سیستم جرم و فنری که چنین حرکتی داشته باشد، یک نوسانگر هارمونیک است و مقدار
ωn، بیان کننده فرکانس طبیعی ارتعاشات آزاد خواهد بود. روش دیگری برای نوشتن رابطه ۵، عبارت زیر است.$\large A_1 \:= \:A \cos \phi \\~\\
\large A_2 \:= \:A \sin \phi$
(رابطه ۷)در رابطههای بالا، ثابتهای جدید A و ϕ را معرفی کردهایم که به ترتیب، دامنه و زاویه فاز را مشخص میکنند و برحسب A1 و A2 قابل تعریف هستند.$\large A\: =\: (A^2 _1 \:+ \:A^2 _2) ^{1/2} \:= \:[x^2 _0 \:+ (\frac {\dot{x} _0} {\omega _n}) ^{2}] ^{1/2} \\~\\
\large \phi \:= \:\tan ^{-1}(\frac {A_2} {A_1}) \:= \:\tan ^{-1} (\frac {\dot{x} _0} {x_0 \omega _n})$
با ادغام رابطههای ۵ و ۷، معادله حرکت را به صورت زیر مینویسیم.$\large x(t)\: =\: A\cos (\omega _nt \:- \:\phi)$
(رابطه ۸)
ماهیت نوسان هارمونیک را میتوان به صورت شماتیک و به شکل زیر (قسمت الف) نشان داد. اگر$\large \overrightarrow{A}$
، برداری با اندازه A باشد که نسبت به محور x، زاویهای برابر $\large \omega _nt \:- \:\phi$
میسازد، رابطه ۸، به عنوان تصویر بردار $\large \overrightarrow{A}$
روی محور x در نظر گرفته میشود. ثابتهای A1 و A2 در رابطه ۵ که به صورت رابطه شماره ۷ تعریف شدهاند، مؤلفههای بردار
$\large \overrightarrow{A}$ در راستای دو محور متعامدی هستند که نسبت به بردار $\large \overrightarrow{A}$
، زاویههای ϕ و $\large -\:(\frac {\pi} {2} \:- \:\phi)$
را میسازند.
نوسان هارمونیک
از آنجایی که زاویه $\large \omega_nt \:- \:\phi$
تابعی خطی از زمان است، به صورت خطی با زمان افزایش مییابد. در نتیجه، تمام نمودار، با سرعت زاویهای ωn و در خلاف جهت حرکت عقربههای ساعت دوران میکند. با دوران نمودار (شکل الف)، تصویر بردار
$\large \overrightarrow{A}$ روی محور x به صورت هارمونیک تغییر میکند. بنابراین، زمانی که بردار $\large \overrightarrow{A}$
زاویهای برابر $\large 2\pi$ را پشت سر بگذارد، حرکت تکرار میشود. تصویر بردار
$\large \overrightarrow{A}$ که آن را با x(t)
نشان میدهیم، در نمودار شکل بالا به عنوان تابعی از $\large \omega _nt$
(قسمت ب) و تابعی از زمان (قسمت پ) رسم شده است. در سیستم جرم و فنر، چند نکته را باید مد نظر قرار داد.
الف) اگر ارتعاشات آزاد سیستم جرم و فنر در مسیر عمودی قرار داشته باشد، فرکانس طبیعی و ثابت فنر را میتوان به ترتیب به صورت $\large k \:= \:\frac {mg} {\delta _{st}}$
و $\large \omega _n \:= \:(\frac {k} {m}) ^{1/2}$
تعریف کرد. از این رو، فرکانس طبیعی به صورت زیر بازنویسی میشود.$\large \omega _n\:= \:(\frac {g} {\delta _{st}}) ^{1/2}$
اکنون میتوانیم با کمک رابطه بالا، فرکانس طبیعی در واحد دور در ثانیه و همچنین دوره تناوب طبیعی را به شکل زیر نمایش دهیم.$\large f_n \:= \:\frac {1} {2\pi} (\frac {g} {\delta _{st}}) ^{1/2} \\~\\
\large \tau_n \:= \:\frac {1} {f_n} \:= \:2\pi (\frac {\delta _{st}} {g}) ^{1/2}$
بنابراین، هنگامی که جرم در مسیر افقی نوسان میکند، فقط با اندازهگیری جابجایی استاتیکی
$\large \delta _{st}$ میتوان فرکانس طبیعی و دوره تناوب ارتعاشات آزاد را به دست آورد و نیازی به دانستن مقادیر
k و m نیست.ب) با کمک رابطه ۸، سرعت $\large \dot{x} (t)$
˙ و شتاب $\large \ddot{x} (t)$
¨ جرم m در لحظه t قابل محاسبه است.$\large \dot{x} (t) \:= \:\frac{\text{d}x}{\text{d}t} (t) \:= \:- \:\omega _nA \sin (\omega _nt \:- \:\phi) \:= \:\omega _nA \cos (\omega _nt \:- \:\phi \:+ \:\frac {\pi} {2}) \\~\\
\large \ddot{x} (t) \:= \:\frac{\text{d} ^2x}{\text{d} t^2} (t) \:= \:- \:\omega ^2 _nA \cos (\omega _nt \:- \:\phi) \:= \:\omega ^2_nA \cos (\omega _nt \:- \:\phi \:+ \:\pi)$
پ) اگر جابجایی اولیه x0 صفر باشد، پاسخ رابطه ۸ به صورت زیر ساده میشود.$\large x_t \:= \:\frac {\dot {x} _0} {\omega _n} \cos (\omega _nt \:- \:\frac {\pi} {2}) \:= \:\frac {\dot{x} _0} {\omega _n} \sin \omega _nt$
اما اگر سرعت اولیه $\large \dot{x} _0$
صفر باشد، پاسخ به شکل زیر خواهد بود.$\large x(t) \:= \:x_0 \sin (\omega _nt \:+ \:\frac{\pi} {2}) \\~\\
\large x(t) \:= \:x_0 \cos \omega_ nt$
ت) پاسخ سیستم یک درجه آزادی را میتوانیم در صفحه جابجایی--سرعت بیان کنیم که به فضای حالت یا صفحه فاز معروف است. به این منظور، رابطه ۸ را در نظر بگیرید که به شیوه زیر نیز نوشته میشود.
$\large \cos (\omega _nt \:- \:\phi) \:= \:\frac {x} {A}$
(رابطه ۹)با مشتقگیری از این رابطه، معادله سرعت به صورت زیر است.$\large \dot{x} (t) \:= \:-A \omega _n\sin (\omega _nt \:- \:\phi) \\~\\
\large \sin (\omega _nt \:- \:\phi) \:= \:-\frac {\dot{x}} {A\omega_n} \:= \:-\frac {y} {A}$
(رابطه ۱۰)در رابطه اخیر، $\large y \:= \:\frac {\dot {x}} {\omega _n}$
برقرار است. اگر طرفین رابطههای ۹ و ۱۰ را به توان ۲ برسانیم، حاصلجمع آنها برابر با واحد خواهد بود.$\large \large \cos^2 (\omega _nt \:- \:\phi) \:+ \:\sin ^2(\omega _nt \:- \:\phi) \:= \:1 \\~\\
\large \frac {x^2} {A^2} \:+ \:\frac {y^2} {A^2} \:= \:1$
به شکل زیر توجه کنید. نمودار مربوط به رابطه ۱۱ در صفحه (y و x)، یک دایره را نشان میدهد (قسمت الف) که بیانکننده صفحه فاز یا فضای حالت از ارتعاشات آزاد سیستم نامیرا است. شعاع دایره (
A) با استفاده از شرایط اولیه حرکت به دست میآید. از سوی دیگر اگر نمودار رابطه ۱۱ را در صفحه (˙x و x) رسم کنیم، شکل حاصل، یک بیضی (قسمت ب) خواهد بود.
نمودار فضای حالت
مثال ۱ -- پاسخ هارمونیک در ارتعاشات آزاد مخزن آب
سؤال: ستون مخزن آب نشان داده شده در شکل زیر، ارتفاعی به اندازه
300ft دارد و از بتن مسلح ساخته شده است. قطر داخلی و خارجی سطح مقطع این ستون، به ترتیب 8ft و 10ft
است. اگر وزن مخزن پر از آب، $\large 6\times10 ^5 \:lb$
باشد، با صرف نظر از جرم ستون، موارد زیر را تعیین کنید. مدول یانگ را برای بتن مسلح $\large 4\times10 ^6 \:psi$
در نظر بگیرید.الف) فرکانس طبیعی و دوره تناوب زمانی مربوط به ارتعاش عرضی مخزن آب
ب) پاسخ ارتعاشی مخزن آب ناشی از جابجایی عرضی اولیه به اندازه $\large 10 \:in$
پ) ماکسیمم مقدار سرعت و شتاب مخزن آب
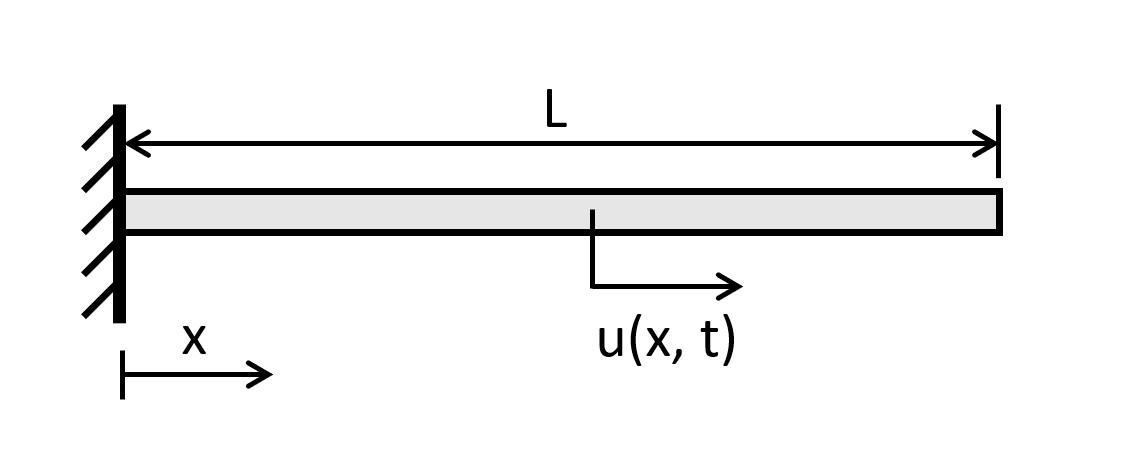
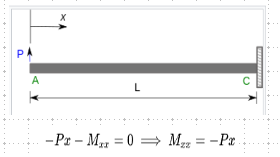
پاسخ: ابتدا مخزن آب را به عنوان جرم نقطهای در نظر میگیریم. سطح مقطع ستون، یکنواخت و جرم آن، قابل صرفنظر کردن است. در نتیجه، سیستم را به صورت تیر یک سر گیردار مدل میکنیم. الف) با توجه به مطالب مندرج در مقاله تحلیل تنش و تغییر شکل در تیرها که قبلاً در مجله فرادرس منتشر شده است، جابجایی عرضی تیر δ به دلیل اعمال بار P
به صورت زیر محاسبه میشود.$\large \delta \:= \:\frac {Pl^3} {3EI}$
در رابطه بالا، E مدول یانگ و I ممان اینرسی مربوط به سطح مقطع تیر است. سفتی تیر (ستون مخزن) را میتوان با کمک رابطه زیر به دست آورد.
$\large k\: =\: \frac {P} {\delta} \:= \:\frac {3EI} {l^3}$
الف) در این مثال، ممان اینرسی سطح مقطع تیر و سفتی آن به صورت زیر است.$\large I \:= \:\frac {\pi} {64} (d^4 _o \:- \:d^4 _i) \:= \:\frac {\pi} {64} (120^4 \:- \:96^4) \:= \:600.9554 \:\times \:10^4 \:in ^4 \\~\\
\large k\: =\: \frac {3 (4\:\times \:10^6) (600.9554 \:\times \:10^4)} {3600^3} \:= \:1545.6672 \:lb/in$
برای محاسبه فرکانس و دوره تناوب طبیعی مخزن آب در ارتعاشات آزاد در جهت عرضی به طریق زیر عمل میکنیم.
$\large \omega_n \:= \:\sqrt {\frac {k} {m}} \:= \:\sqrt {\frac {1545.6672 \:\times \:386.4} {6 \:\times \:10^5}} \:= \:0.9977 \:rad /sec \\~\\
\large \tau_n \:= \:\frac {2\pi} {\omega _n} \:= \:\frac {2\pi} {0.9977} \:= \:6.2977 \:sec$
هنگامی که جابجایی و سرعت اولیه به ترتیب برابر $\large x_0 \:= \:10 \:in$ و ˙x0=0 باشد، پاسخ هارمونیک این سیستم در ارتعاشات آزاد به شیوه زیر محاسبه میشود.
$\large x(t) \:= \:A_0 \sin (\omega _nt \:+ \:\phi_0)$
از طرفی، میدانیم جابجایی عرضی (A0) و زاویه فاز (ϕ0) اولیه برابر با مقادیر زیر است.$\large A_0 \:= \:[x^2 _0\: +\: (\frac {\dot{x}_0} {\omega_n}) ^2] ^{1/2} \:= \:x_0 \:= \:10 \:in \\~\\
\large \phi_0 \:= \:\tan ^{-1} (\frac {x_0 \omega_n} {0}) \:= \:\frac {\pi} {2}$
اکنون با جایگذاری مقادیر بالا، پاسخ ارتعاشی قابل محاسبه است.$\large x(t) \:= \:10 \sin (0.9977t \:+ \:\frac {\pi} {2}) \:= \:\cos (0.9977t) \:in$ر از رابطه اخیر مشتق بگیریم، سرعت و سپس شتاب مخزن آب به راحتی به دست میآیند.
$\large \dot{x}(t) \:= \:10 (0.9977) \:\cos (0.9977t \:+ \:\frac {\pi} {2}) \\~\\
\large \dot{x} _{\max} \:= \:A_0 \omega_n \:= \:10(0.9977) \:= \:9.977 \:in /sec \\~\\
\large \ddot{x}(t) \:= \:-\:10 (0.9977) ^2\sin (0.9977t \:+ \:\frac {\pi} {2}) \\~\\
\large \ddot{x}_{\max} \:= \:A_0 (\omega_n)^2 \:= \:10 (0.9977)^2 \:= \:9.9540 \:in /sec^2$
ارتعاشات آزاد سیستم های نامیرا در حرکت پیچشی
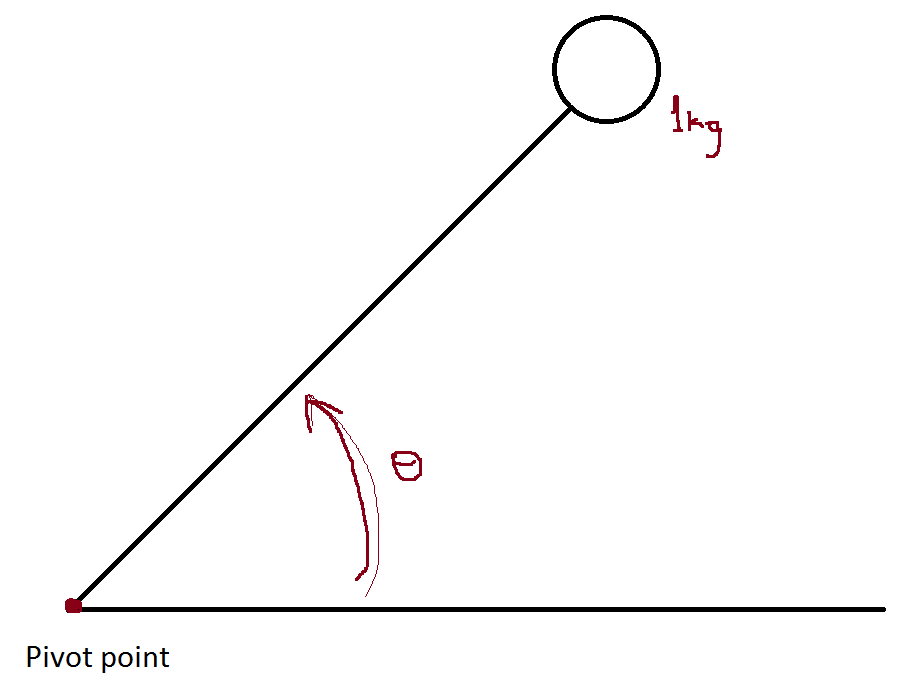
اگر جسم صلبی حول یک محور مرجع دوران کند، حرکت آن به صورت ارتعاشات پیچشی خواهد بود. در این مورد، جابجایی جسم برحسب یک مختصات زاویهای اندازهگیری میشود. در ارتعاشات آزاد پیچشی، ممان بازگرداننده، از پیچش یک عضو الاستیک یا به دلیل یک ممان خنثی نشدهای ناشی میشود که یک نیرو یا کوپل، آن را به وجود آورده است. شکل زیر، دیسکی را نشان میدهد که ممان اینرسی قطبی جرم آن برابر
$\large J_0$
بوده و در انتهای یک شفت صلب مدوّر قرار دارد.
انتهای دیگر شفت، ثابت شده است. فرض کنید دوران زاویهای دیسک، حول محور شفت را با زاویه θ تعریف کنیم و این زاویه، نشان دهنده زاویه پیچش شفت هم باشد. همانطور که در مقاله تحلیل میله های تحت پیچش دیدهایم، در پیچش شفتهای دایرهای، رابطه زیر برقرار است.
ارتعاشات پیچشی$\large M_t \:= \:\frac {G I_0} {l} \theta$
در این رابطه، $\large M_t$ گشتاوری است که منجر به پیچشی به اندازه θ میشود. مدول برشی و طول شفت به ترتیب با G و l نشان داده شدهاند.
I0 نیز ممان اینرسی قطبی مربوط به سطح مقطع شفت است که با کمک رابطه زیر به دست میآید.$\large I_0 \:= \:\frac {\pi d^4} {32}$
قطر شفت با d نشان داده شده است. اگر دیسک به اندازه θ نسبت به موقعیت تعادلش جابجا شود، گشتاور بازدارندهای با بزرگی
$\large M_t$ ایجاد میشود. بنابراین، به عنوان یک فنر پیچشی عمل میکند که ثابت این فنر پیچشی به صورت زیر محاسبه میشود.$\large M_t$
$\large k_t \:= \: \frac {M_t} {\theta} \:= \:\frac {GI_0} {l} \:= \:\frac {\pi Gd ^4} {32l}$
معادله حرکت زاویهای دیسک، حول محورش را میتوان با استفاده از قانون دوم نیوتن نتیجه گرفت. با در نظر گرفتن نمودار جسم آزاد(free body diagram) رسم شده دیسک در شکل قبل و با اعمال قانون دوم نیوتن، معادله حرکت قابل استخراج است.$\large J_0 \ddot{\theta} \:+ \:k_t \theta \:=\:0$
(رابطه ۱۲)
همانطور که میبینید این رابطه مشابه رابطه ۳ در ابتدای این مبحثمه. اگر ممان اینرسی قطبی J0، جابجایی زاویهای θ و ثابت فنر پیچشی$\large k_t$
را به ترتیب با جرم m، جابجایی x و ثابت فنر خطی k جایگزین کنیم، به همان رابطه خواهیم رسید. از این رو، فرکانس طبیعی سیستم پیچشی در ارتعاشات آزاد با کمک رابطه زیر به دست میآید.$\large \omega_n \:= \:(\frac {k_t} {J_0}) ^{1/2}$
(رابطه ۱۳)
دوره و فرکانس ارتعاشات آزاد برحسب دور در ثانیه به قرار زیر است.$\large \tau_n \:= \:2\pi (\frac {J_0} {k_t}) ^{1/2} \\~\\
\large f_n \:= \:\frac {1} {2\pi} (\frac {k_t} {J_0}) ^{1/2}$
در مورد این سیستم باید چند نکته را مد نظر قرار داد.ممان اینرسی قطبی مربوط به جرم یک دیسک را میتوان با استفاده از رابطه
$\large J_0 \:= \:\frac {\rho h\pi D^4} {32} \:= \:\frac {W D^4} {8g}$
به دست آورد. در رابطه بالا، ρ چگالی، h ضخامت و D قطر دیسک را نشان میدهد و وزن آن برابر W است.
به سیستم اینرسی--فنر پیچشی نشان داده شده در شکل قبل، آونگ پیچشی گفته میشود. یکی از مهمترین کاربردهای آونگ پیچشی در ساعتهای مکانیکی است. در این ساعتها، چرخدنده و شیطانک (Pawl)، نوسان یک آونگ پیچشی کوچک را به حرکت عقربهها تبدیل میکند.
برای به دست آوردن پاسخ عمومی رابطه ۱۲، مانند رابطه ۳ عمل میکنیم.$\large \theta (t) \:= \:A_1 \cos \omega _nt \:+ \:A_2 \sin \omega _nt$
با کمک رابطه ۱۳، ضرایب A1 و A2 را با کمک شرایط اولیه به دست میآوریم.$\large \theta (t\:= \:0) \:= \:\theta _0 \\~\\
\large \dot{ \theta} (t \:= \:0) \:= \:\frac{\text {d} \theta}{\text {d} t} (t \:= \:0) \:= \:\dot{ \theta} _0 \\~\\
\large \Rightarrow ~~~ A_1 \:= \:\theta _0 \\~\\
\large \Rightarrow ~~~ A_2 \:= \:\frac {\dot{\theta} _0} {\omega _n}$
من در حال مطالعه ارتعاشات هستم. بنابراین من از کتاب Beer-Johnston-Cornwell Dynamics استفاده می کنم. من نگران معادله ارتعاش کم میرایی هستم که در کتاب این است:
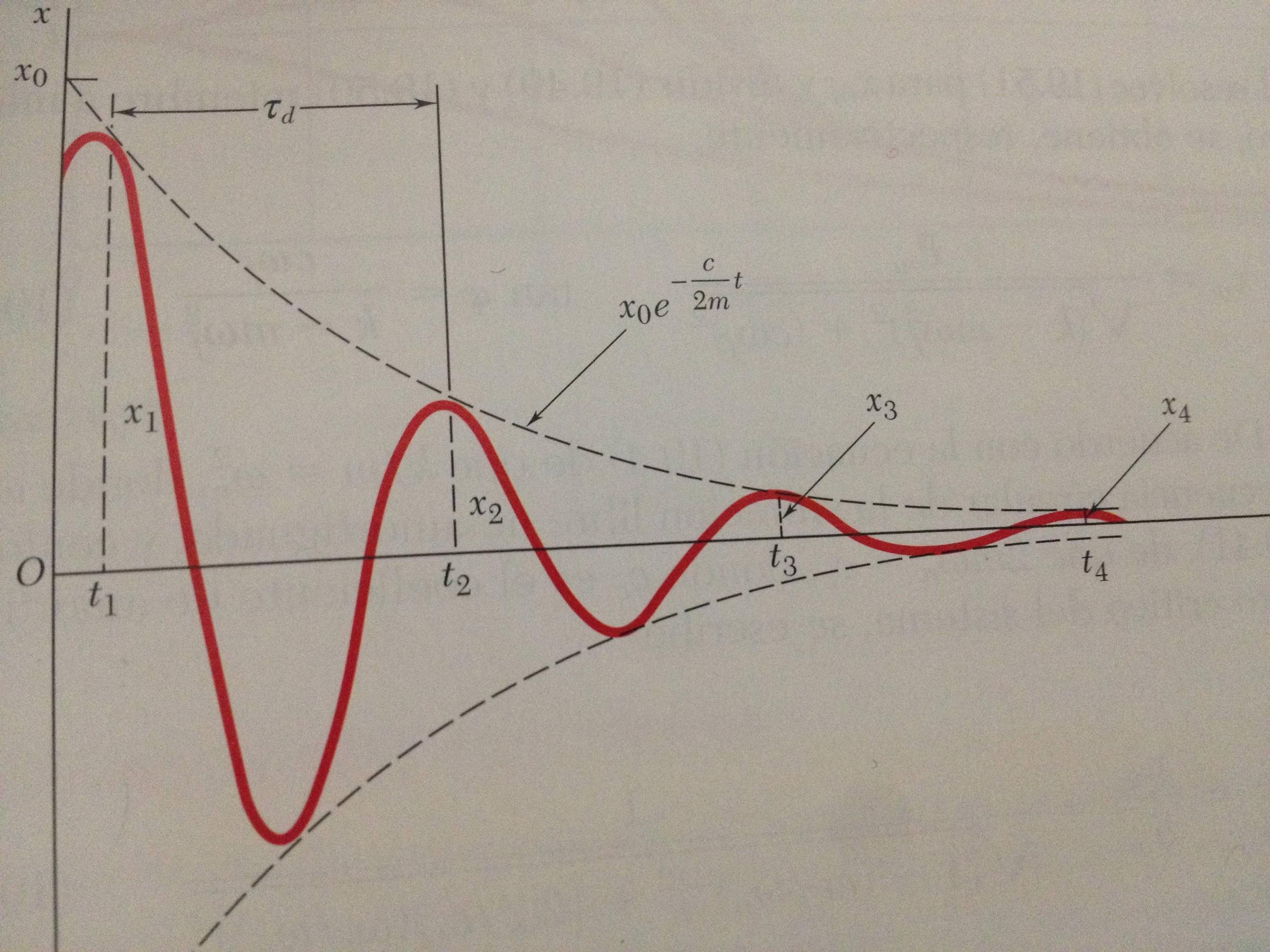
$x_{(t)}=x_0e^{-\lambda t}\sin(\omega_d+\phi)$
جایی که$\omega_d=\sqrt{\omega_n^2+c^2/4m^2}$
من فکر می کنم که $x_0$ با بردار نتیجه ثابت c1 جایگزین می شود و c2 تحت تاثیر عامل$e^{-\lambda t}$. یعنی$x_m$
یا یک دامنه، اما نه موقعیت اولیه، زیرا می تواند 0 باشد، با سرعت اولیه.
همچنین، نمودار معادله مرزی را با x0 نشان میدهد
میشه کمکم کنید و نظر بدید چگونه باید x0 را تفسیر کنم ? شاید من این موضوع را اشتباه متوجه شده ام
به نظرم x0 متناسب با اولیه$\sqrt{E_{initial}}$ است
جذر انرژی اولیه در سیستم برای مثال فرض کنید حرکت یک جرم را روی یک فنر و x ریخته ایم
فاصله از موقعیت تعادل است. انرژی اولیه سیستم می تواند به طور کامل در کشش فنر باشد (سرعت اولیه صفر).
انرژی اولیه اولیه$E_{initial} = \frac12k\,x_{initial}^2 = \frac12k\,x_0^2$ است
به طور کلی برای سیستم در مثال$x_0=\sqrt{2\frac{E_{initial}}{k}}$
ما می توانیم توزیع انرژی اولیه را بین انرژی پتانسیل و انرژی جنبشی تغییر دهیم (تغییر ϕ) اما اگر مجموع انرژی اولیه یکسان باشد x0 نیز همینطور است.
حل معادله دیفرانسیل نوسانگر میرایی
اصطکاک استوکس
می گوید که اصطکاک استوکس خواهد بود
$F = -m \gamma \dot{x}.$
برای من، هیچ منطقی نیست که چرا به جرم جسم بستگی دارد. این بدان معنی است که کاهش سرعت به جرم بستگی ندارد. یا فقط از آنجایی که متناسب با حجم است و حجم آن معمولاً به جرم بستگی دارد.
ترکیب خطی راه حل ها
سپس معادله دیفرانسیل تنظیم می شود، من کاملاً آن را درک می کنم، به جز سردرگمی در مورد اصطکاک.
$m \ddot{x} + \gamma \dot{x} + \omega_0^2 = 0$با$\delta = \frac{\gamma}{2}$
و$\omega = \sqrt{\omega_0^2 - \delta^2}$راه حل برای$x(t) = \exp(\lambda t)$رویکرد هستند
$\lambda = -\delta \pm i \omega t$.
یکی از انواع مثبت یا منفی راه حل معتبری است، اما ترکیب خطی هر دو راه حل هستند. میفهمم، متوجه هستم، درک میکنم.
سپس کتاب می گوید که راه حل کلی ترکیب اجزای واقعی و خیالی است. از طرف دیگر، می توان یک زاویه فاز اضافه کرد و یک راه حل "فشرده" مانند این داشت:
$x(t) = x_0 \exp(-\delta t) \exp(i ( \omega t + \phi ) )$ مطمئناً ترکیبی خطی از اجزای واقعی و خیالی را تشکیل می دهد، اما این ترکیب چگونه است$\exp(i \phi)$
$c_1 \exp(i\omega t) + c_2 \exp(-i\omega t) ?$ویرایش: پاسخ زیر$F = -m \omega^2_0 x$ را نادیده می گیرد
اصطلاح و بنابراین فقط برای مشکلاتی که فقط میرایی بدون کشش دارند کاربرد دارد.
در اینجا روش مستقیم مقابله با این مشکل بدون نیاز به حدس زدن به عنوان راه حل است.
$F = m \ddot{x}$
$F = m \ddot{x} = -m \gamma \dot{x}$
$\dot{v} = -\gamma v \text{ with } v = \dot{x}$
$\frac{\rm d}{{\rm d} t}v=-\gamma v$
$\frac{1}{v}{\rm d}v = -\gamma\, {\rm d} t$
$\int{\frac{1}{v}{\rm d}v} = -\int{\gamma\, {\rm d} t}$
اگر شرایط اولیه $v(0)=v_0$باشد
سپس
$\int_{v_0}^{v} \frac{1}{v}{\rm d}v = -\int_0^t \gamma\, {\rm d} t$
$\ln\frac{v}{v_0} =-\gamma t$
$v = v_0 \exp({-\gamma t})$
سپس
$x(0)=x_0$بنابراین اگر بتوانید سیستمی با شکل$\ddot{x}=-\gamma\,\dot{x}$˙ تولید کنید
سپس راه حل از $\gamma$ استفاده می کند
ضریب در تابع فروپاشی نمایی.