در مکانیک نیوتنی با معادلات مختلفی برای انواع حرکت جسم رو به رو میشویم. همان طور که بالاتر نیز بیان شد سادهترین حالت این است که یک جسم نقطهای را در نظر بگیریم که تحت تاثیر چندین نیرو حرکت میکند و با معادله برداری زیر بیان میشود:$\large \frac{d \overrightarrow{p}}{d t}=\overrightarrow{F}\ (1)$ و ایم یک اصل هست$\overrightarrow p=m\overrightarrow v$ این معادله حرکت را نمیتوان از چند معادله دیگر استخراج کرد

همچنین میتوان این دیدگاه را داشت که یکی از سه کمیت جرم سکون، نیرو و شتاب براساس دو کمیت دیگر تعریف شده است. $\large \frac{d \overrightarrow{L}}{d t}=\overrightarrow{\tau} \ (2)$معادله بالا را میتوان با تصور این که جسم از تعداد زیادی ذرات کوچک و تقریباً نقطهای کنار هم قرار گرفته است که موقعیت نسبی آنها ثابت است (شرایط جسم صلب) به دست آورد. بیشترین چیزی که برای معادله بالا مورد نیاز است محدودیت سینماتیکی صلب و تعاریف مناسب برای حرکت زاویهای یعنی L و گشتاور $\tau$ است.همچنین در مکانیک نیوتنی اشکال مختلفی از معادله بالا را که در پایههای غیر خطی و به عنوان مثال مختصات قطبی نوشته میشود، دیدهایم. اگر چه ممکن است این معادله در مثلاً مختصات قطبی بلافاصله به عنوان معادلهبالا قابل تشخیص نباشد اما با بررسی این اشکال از معادلات متوجه میشویم که این معادلات حاوی اطلاعات بیشتری نسبت به آنچه در معادله بالا نشان داده شده نیستند بلکه فقط نشان دهنده انتخاب مختصات مناسب برای برخی مسائل است. علاوه بر این ما با اصول انرژی، تکانه خطی و تکانه زاویهای برخورد کردهایم که میگوید در شرایط خاص برخی از این مقادیر بر حسب جرم و سرعت یعنی از نظر جنبشی با گذشت زمان تغییر نمیکنند یا در موارد دیگر میزان تغییر آنها را پیش بینی میکنند. اینها مواردی است که میتوان از معادله اول یا مشتق آن یعنی معادلهدوم استنباط کرد.
بدین ترتیب میتوان دید که اگر چه تنوع زیادی از معادلات مختلف به دست آمده و مورد استفاده قرار میگیرد اما همه آنها دارای یک ریشه مشترک هستند و آن معادله حرکت یک ذره نقطهای واحد است. مسأله موضوع مکانیک تحلیلی این است که همه اشکال مختلف معادلات حرکت را که در زمینههای مختلف اعمال میشوند را در یک موقعیت مساوی قرار دهیم. در حقیقت همه آنها به صورت یکسان و مجموعهای از معادلات یعنی معادله لاگرانژ و بعدها به صورت معادلات هامیلتونی بیان خواهند شد. همچنین این معادلات از یک اصل اساسی مشتق میشوند.که به آن اصل کنش میگوییم.
همچنین یکی از مفیدترین و مهمترین ویژگیهای معادلات لاگرانژ و هامیلتونی را مشاهده خواهیم کرد و این ویژگی مهم این است که این دو کمیت مستقل از انتخاب مختصات، شکل یکسانی دارند. این امر این پارامترها را در برخورد با سیستمهایی که درجه آزادی مناسبی بر حسب متغیرهایی که معادلات حرکت نیوتن در آنها به سختی قابل نوشتن است، برای مثال معرفی نیروهایی در مکانیک نیوتنی که تنها وظیفه آنها برآورده ساختن شرایط سینماتیکی است، مثلاً نیرویی در طناب با طول ثابت و سیستمهای محدود، بسیار قدرتمند میکند.اساسیترین ویژگی یک سیستم فیزیکی، درجه آزادی آن است. این حداقل تعداد متغیرهایی است که برای تعیین کامل موقعیت همه ذرات و اجسام بخشی از سیستم، یعنی پیکربندی آن در یک زمان معین مورد نیاز است. اگر تعداد درجات آزادی یک مجموعه N باشد هر مجموعهای از متغیرهای $q^1,\ . \ . \ . \ ,\ q^N$ پیکربندی سیستم را مشخص میکند و مختصات تعمیم یافته سیستم نامیده میشود. توجه داشته باشید که نحوه حرکت سیستم در مختصات تعمیم یافته گنجانده نشده اما در مشتقات زمانی آنها یعنی $\dot{q}^1,\ . \ . \ . \ ,\ \dot{q}^N$ وجود دارد.
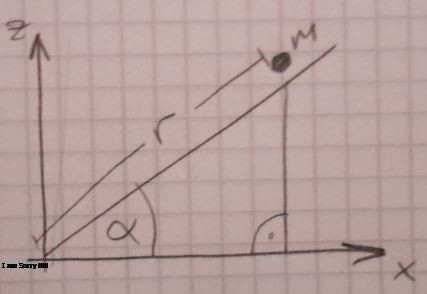
برای مثال یک ذره در حال حرکت را در نظر بگیرید که یک درجه آزادی دارد. مختصات تعمیم یافته این ذره را میتوان به صورت x نوشت. ذرهای که در سه راستا حرکت میکند دارای سه درجه آزادی است و مثالی از مختصات تعمیم یافته آن به صورت $\overrightarrow{r}=(x,y,z)$ است، این مختصات در سیستم کروی به صورت $\overrightarrow{r}=(r,\theta,\phi)$ است که $x=r \sin \theta \cos \phi, \ y=r \sin \theta \sin \phi, \ z=r \cos \theta$ نمایش داده میشود.
تعداد درجات آزادی برابر با تعداد معادلات حرکتی است که برای یافتن حرکت سیستم لازم است. گاهی اوقات بهتر است از تعداد بیشتری از مختصات نسبت به تعداد درجات آزادی یک سیستم استفاده کنیم. سپس مختصات باید از طریق نوعی معادله که قید نامیده می شود به یکدیگر مرتبط شوند. تعداد درجات آزادی در چنین حالتی برابر با تعداد مختصات تعمیم یافته منهای تعداد محدودیتها است.برای مثال یک پاندول را در نظر بگیرید که توسط دو مختصه مستقیم (x,y) و یک جرم که به یک سر طناب بسته شده است، در نظر گرفته میشود. مختصات تعمیم یافته در این حالت زاویه است و درجه آزادی این سیستم یک است و (x,y) توسط قید$x^2+y^2=l^2$ که l طول طناب است به یکدیگر مرتبط میشوند
فرض کنید که یک سیستم شامل تعدادی ذرات به صورت نقطهای است که مختصات عادی آنها برابر با $x^1, .\ .\ .\ ,x^N$ است. همچنین پیکربندی سیستم توسط مختصات تعمیم یافته $q^1, .\ .\ .\ ,q^N$ داده میشود. در این حالت نمیخواهیم تعداد ابعاد حرکت ذرات و در حقیقت تعداد درجات آزادی سیستم را مشخص کنیم. این درجات آزادی میتواند برای n ذره که در صفحه حرکت میکنند برابر با N=2n و برای m ذره که در سه بُعد حرکت میکنند N=3m باشد. همچنین با توجه به اینکه هر دو مختصات بیان شده در بالا پیکربندی سیستم را مشخص میکنند، باید بین آنها یک رابطه باشد که به صورت زیر بیان میشود:$\large \begin{aligned}
&x^{1}=x^{1}\left(q^{1}, q^{2}, \ldots, q^{N}\right)=x^{1}(q) \\
&x^{2}=x^{2}\left(q^{1}, q^{2}, \ldots, q^{N}\right)=x^{2}(q) \\
&\vdots \\
&x^{N}=x^{N}\left(q^{1}, q^{2}, \ldots, q^{N}\right)=x^{N}(q)
\end{aligned}$که در حالت فشرده این رابطه میان مختصات را میتوان به صورت $x^{i}=x^{i}(q)$ نوشت. برای ایجاد ارتباط بین دو مجموعه متغیر که پیکربندی را کاملاً مشخص میکنند، توابع $x^i$میتوانند وابستگی زمانی مشخصی را شامل شوند که در این قسمت ترجیح میدهیم این توابع به زمان وابسته نباشند. اگر در متغیرهای $q^i$ یک جابجایی بی نهایت کوچک برابر با $dq^i$ ایجاد کنیم، قاعده مشتق زنجیرهای نشان میدهد که این جابجایی مربوطه در $x^i$برابر است با:$\large d x^{i}=\sum_{j=1}^{N} \frac{\partial x^{i}}{\partial q^{j}} d q^{j}$کار انجام شده در این جابهجایی برابر با حاصلضرب نیرو و جابهجایی است که به صورت زیر بیان میشود و داریم:
$\large d W=\sum_{i=1}^{N} F_{i} d x^{i}=\sum_{i=1}^{N} \mathscr{F}_{i} d q^{i}$
که F برابر است با$\large \mathscr{F}_{i}=\sum_{j=1}^{N} F_{j} \frac{\partial x^{j}}{\partial q^{i}}$
برابر با نیروی تعمیم یافته است که به مختصات تعمیم یافته یعنی $\mathscr{F}_i$ ارتباط دارد. همان طور که در مورد سرعت تعمیم یافته گفته شد، نیازی نیست که بُعد
$\mathscr{q}_i$ همانند نیروی معمولی باشد. به عنوان مثال یک پاندول به طول l را در نظر بگیرید که مختصات تعمیم یافته برای این پاندول ϕ است و به عنوان زاویه از محور عمودی شناخته میشود. فرض کنید که جرم m تحت زاویه dϕ و تحت اثر نیروی $\overrightarrow{F}$ حرکت میکند. جابهجایی این جرم برابر با $d\overrightarrow{r}=l\ d\phi \ \hat{\phi}$ و کار در این جابهجایی کوچک برابر با $dW=\overrightarrow{F}.d\overrightarrow{r}=F_{\phi}ld\phi$
است. نیروی تعمیم یافته که مرتبط با مختصات زاویهای ϕ است برابر با $\mathscr{F}_{\phi}=F_{\phi}l$
بوده که دقیقاً برابر با گشتاور نیرو است. پس نتیجهای که از این مثال حاصل میشود بسیار عمومی است و این است که نیروی تعمیم یافته برای مختصات زاویهای برابر با گشتاور حرکت است. اگر نیرو پایستار باشد، از رابطه بین پتانسیل و نیرو داریم:$\large F_{i}=-\frac{\partial V}{\partial x^{i}}$
اگر این رابطه را در رابطه مربوط به نیروی تعمیم یافته وارد کنیم خواهیم داشت:
$\large \mathscr{F}_{i}=-\sum_{j=1}^{N} \frac{\partial V}{\partial x^{j}} \frac{\partial x^{j}}{\partial q^{i}}=-\frac{\partial V}{\partial q^{i}}$
رابطه میان پتانسیل و نیروی تعمیم یافته به ازای هر مختصات تعمیم یافته شکل بالا را دارد.
انرژی جنبشی و تکانه تعمیم یافته چیست؟در این قسمت بررسی میکنیم که انرژی جنبشی چه رابطهای با مختصات تعمیم یافته و مشتقات آن یعنی سرعت تعمیم یافته دارد. یک تک ذره با جرم m که در سه بُعد حرکات میکند در نظر بگیرید که در نتیجه درجات آزادی آن برابر با N=3 است. در این حالت انرژی جنبشی برابر است با:$\large T=\frac{1}{2} m \sum_{i=1}^{3}\left(\dot{x}^{i}\right)^{2}$در رابطه
$\large \dot{x}^{i}=\sum_{j=1}^{3} \frac{\partial x^{i}}{\partial q^{j}} \dot{q}^{j}$
نشان دادیم که $\dot{x}^{i}$ تابعی از $q^j$ است و $\dot{q}^{j}$ زمانی وارد میشود که مختصات به زمان وابسته باشد. بدین ترتیب میتوان رابطه انرژی جنبشی را بر حسب مختصات و سرعت تعمیم یافته به شکل زیر نوشت و داریم:$\large T=\frac{1}{2} m \sum_{i, j=1}^{3} A_{i j}(q) \dot{q}^{i} \dot{q}^{j}$
اگر بخواهیم این رابطه را بر حسب ساختار ماتریسی بنویسیم، داریم:$\large T=\frac{1}{2} m \dot{q}^{t} A \dot{q}$
که در آن ماتریس A برابر است با:$\large A_{i j}=\sum_{k=1}^{3} \frac{\partial x^{k}}{\partial q^{i}} \frac{\partial x^{k}}{\partial q^{j}}$
ذکر این نکته مهم است که بدانید اگر چه ممکن است که رابطه بین مختصات معمولی و مختصات تعمیم یافته غیرخطی باشد، اما رابطه انرژی جنبشی و سرعت تعمیم با ضریب
$A_{ij}$ همواره خطی است و تنها به مختصات تعمیم یافته بستگی دارد. برای مثال حرکت در صفحه را برای مختصات قطبی در نظر بگیرید که داریم:
$\large \begin{aligned}
&x=r \cos \phi, \\
&y=r \sin \phi,
\end{aligned}$
بدین ترتیب ماتریس A برابر است با
$\large A=\left[\begin{array}{ll}
A_{r \tau} & A_{r \phi} \\
A_{r \phi} & A_{\phi \phi}
\end{array}\right]=\left[\begin{array}{cc}
1 & 0 \\
0 & r^{2}
\end{array}\right]$
و انرژی جنبشی به شکل شناخته شده زیر به دست میآید و داریم:
$\large T=\frac{1}{2} m\left(\dot{r}^{2}+r^{2} \dot{\phi}^{2}\right)$
اگر از انرژی جنبشی نسبت به یکی از سرعتها در مختصات عادی (یعنی
$v^i=\dot{x}^i$) دیفرانسیل بگیریم، داریم:
$\large \frac{\partial T}{\partial \dot{x}^{i}}=m \dot{x}^{i}$
که در حقیقت تکانه خطی به دست میآید. تکانه تعمیم یافته را به روشی مشابه میتوان به صورت زیر نوشت و داریم:
$\large p_{i}=\frac{\partial T}{\partial \dot{q}^{i}}$
این حقیقت که تکانه تعمیم یافته به متغیرهای زاویهای وابسته است نشان میدهد که تکانه زاویهای یک کمیت عمومی است. در ادامه میخواهیم به معادلات حرکت برگردیم و آنها را بر اساس مختصات تعمیم یافته فرمول بندی کنیم.
تابع لاگرانژ چیست؟
تابع لاگرانژی که لاگرانژین نیز نامیده میشود کمیتی است که وضعیت یک سیستم فیزیکی را مشخص میکند. در ابتدا تابع لاگرانژ را برای یک ذره منفرد بررسی میکنیم. همان طور که نشان دادیم معادله حرکت برای یک تک ذره توسط رابطه (1) داده میشود. در قسمت قبل نشان دادیم که چگونه تکانه از انرژی جنبشی یه دست میآید. بدین ترتیب معادله (1) را به شکل زیر و براساس مختصات تعمیم یافته بازنویسی میکنیم و داریم:
$\large \frac{d}{d t} \frac{\partial T}{\partial \dot{x}^{i}}=F_{i}\ (3)$
اولین حدس این است که اگر مختصات با مختصات تعمیم یافته و نیرو با نیروی تعمیم یافته جایگزین شود، چیزی مشابه معادله بالا به دست میآید. بنابراین ما سمت چپ معادله بالا را با q به جای x جایگزین میکنیم و داریم:$\large \begin{aligned}
\frac{d}{d t} \frac{\partial T}{\partial \dot{q}^{i}} &=\sum_{j=1}^{3} \frac{d}{d t}\left(\frac{\partial T}{\partial \dot{x}^{j}} \frac{\partial \dot{x}^{j}}{\partial \dot{q}^{i}}\right)=\sum_{j=1}^{3} \frac{d}{d t}\left(\frac{\partial T}{\partial \dot{x}^{j}} \frac{\partial x^{j}}{\partial q^{i}}\right)=\\
&=\sum_{j=1}^{3}\left(\frac{\partial x^{j}}{\partial q^{i}} \frac{d}{d t} \frac{\partial T}{\partial \dot{x}^{j}}+\frac{d}{d t} \frac{\partial x^{j}}{\partial q^{i}} \frac{\partial T}{\partial \dot{x}^{j}}\right)=\sum_{j=1}^{3}\left(\frac{\partial x^{j}}{\partial q^{i}} \frac{d}{d t} \frac{\partial T}{\partial \dot{x}^{j}}+\frac{\partial \dot{x}^{j}}{\partial q^{i}} \frac{\partial T}{\partial \dot{x}^{j}}\right)=\\
&=\sum_{j=1}^{3} \frac{\partial x^{j}}{\partial q^{i}} \frac{d}{d t} \frac{\partial T}{\partial \dot{x}^{j}}+\frac{\partial T}{\partial q^{i}}
\end{aligned}$در اینجا، ما از قواعد مشتق زنجیرهای و این واقعیت استفاده می کنیم که T در گام اول به $\dot{x}^{i}$
بستگی دارد و به $\dot{x}^{i}$ وابسته نیست. سپس در مرحله دوم از این واقعیت که $\dot{x}^{i}$
توابع q هستند و نه $\dot{q}^{i}$
ها برای بدست آوردن $\frac{\partial{\dot{x}}^ j}{\partial \dot{q}^{i}}=\frac{\partial{x}^{j}}{\partial q^{i}}$
استفاده میکنیم. در مرحله سوم دوباره از این موضوع برای استخراج رابطه
$\frac{d}{dt}\frac{\partial{x}^{j}}{\partial q^{i}}=\frac{\partial{\dot{x}}^ j}{\partial q^{i}}$
استفاده میشود و در آخرین مرحله دوباره مشتق زنجیرهای در T مورد استفاده قرار میگیرد. حال میتوانیم معادله (3) را در معادلات حرکت ذره قرار دهیم و بدین ترتیب داریم:
$\large \frac{d}{d t} \frac{\partial T}{\partial \dot{q}^{i}}=\sum_{j=1}^{3} \frac{\partial x^{j}}{\partial q^{i}} F_{j}+\frac{\partial T}{\partial q^{i}}$
و در نهایت معادله لاگرانژ حرکت ذره به صورت زیر به دست میآید:
$\large \frac{d}{d t} \frac{\partial T}{\partial \dot{q}^{i}}-\frac{\partial T}{\partial q^{i}}=\mathscr{F}_{i}$
فرمالیزم لاگرانژی در زمانی که انرژی پتانسیل وجود دارد یعنی نیروها پایستار هستند و انرژی مکانیکی نیز پایستار است، بسیار مفید است. در نتیجه نیروی تعمیم یافته به صورت
$\mathscr{F}_{i}=-\frac{\partial V}{\partial q^{i}}$
نوشته میشود و معادله لاگرانژ برابر است با:$\large \frac{d}{d t} \frac{\partial T}{\partial \dot{q}^{i}}-\frac{\partial T}{\partial q^{i}}+\frac{\partial V}{\partial q^{i}}=0$انرژی پتانسیل به سرعت تعمیم یافته وابسته نیست. در نتیجه اگر لاگرانژی را به شکل زیر بنویسیم:L=T−Vمعادلات را میتوان به طور کامل و به صورت زیر بیان کرد:
$\large \frac{d}{d t} \frac{\partial L}{\partial \dot{q}^{i}}-\frac{\partial L}{\partial q^{i}}=0$
تابع L را تابع لاگرانژ یا لاگرانژین مینامیم. این شکل از معادلات حرکت یکی از رایجترین شکلهایی است که برای حل مسائل مکانیک تحلیلی استفاده میشود. مشتق معادلات لاگرانژ در بالا بر اساس موقعیتی بود که مختصات تعمیم یافته $q^i$ استاتیک بودند، یعنی زمانی که تبدیل مختصات بین $q^i$ و مختصات لختی یعنی $x^i$ زمان را شامل نمیشد. این فرض بسیاری از موقعیتهای مهم و مفید مانند سیستمهای مختصات شتابدهنده یا چرخشی را حذف میکند. با این حال میتوان ثابت کرد که معادلات لاگرانژ در مواردی که تغییر بین مختصات لختی و تعمیم یافته دارای وابستگی زمانی مشخص یعنی $x^i=x^i(q;t)$ است همچنان برقرار میماند. در ادامه یک مثال بررسی میکنیم تا نشان دهیم معادلات لاگرانژ، هنگامی که در موقعیتهای وابسته به زمان اعمال میشوند نیروهای لختی شناخته شدهای را بازتولید میکنند و از این امر به عنوان یک نتیجه گیری رسمی استفاده میکنیم. فقط این نکته را به ذهن داشته باشید که زمانی که لاگرانژی را شکل میدهید، انرژی جنبشی، انرژی جنبشی نسبت به سیستم لختی است.یک ذره با جرم m در یک خط حرکت میکند. به جای استفاده از مختصات لختی x، میخواهیم از مختصات تعمیم یافته $q=x-x_0(t)$ استفاده کنیم که x0(t) توسط یک یا چند تابع مشخص میشود. برای مثال توضیح حرکت داخل یک ماشین که در حال حرکت بر روی یک مسیر مستقیم است و $x_0(t)$
موقعیت لختی ماشین است. همچنین تعریف میکنیم که $v_0(t)=\dot{x}_0(t)$و$a_0(t)=\ddot{x}_0(t)$ است. بدین ترتیب انرژی جنبشی برابر است با:
$\large T=\frac{1}{2} m\left(\dot{q}+v_{0}(t)\right)^{2}$
در غیاب نیروها، لاگرانژی به شکل زیر در میآید و داریم:$\large 0=\frac{d}{d t} \frac{\partial T}{\partial \dot{q}}=m\left(\ddot{q}+a_{0}(t)\right)$
در معادله بالا میتوان دید که معادله مشهور نیروی لختی یعنی $-ma_0(t)$
به صورت اتوماتیک وار به دست آمده است. اگر چندین نیرو بر جسم اثر کنند، میتوان نیروی تعمیم یافته را بر اساس نیروی لختی نوشت و داریم
$\mathscr{F}_{q}=F_{x}$. نیروی تعمیم یافته $\mathscr{F}_{q}$
شامل نیروی لختی نیست.همان طور که گفتیم لاگرانژی را میتوان برای سیستمهای چند ذرهای یا بس ذرهای نیز بررسی کرد که در این مطلب از بحث در مورد آن صرف نظر میکنیم.
اصل کنش در مکانیک تحلیلی چیست؟
در این بخش اصلی را بررسی میکنیم که منجر به معادلات حرکت برای هر سیستم مکانیکی میشود. این اصل، اصل کنش است. برای فهم این اصل به کمی دانش ریاضیات نیاز داریم. فرض کنید که یک سیستم مکانیکی داریم و برای مثال فرض کنید یک ذره در پتانسیل در حال حرکت است و نمیدانیم مسیر حرکت ذره چگونه است. با این حال شرایط اولیه به این صورت است که ذره در زمان $t_0$ از مکان $r(t_0)=\overrightarrow{r}_0$ و با سرعت$v(t_0)=\overrightarrow{v}_0$
شروع به حرکت میکند. برای هر مسیر $\overrightarrow{r}(t)$ که شرایط اولیه را برآورده کند، S را به صورت زیر تعریف میکنیم:
$\large S=\int_{t_{0}}^{\infty} d t L$که L لاگرانژی و برابر با T−V است. معادله بالا معادله کنش است. این معادله برای یک ذره با وجود پتانسیل به صورت زیر نوشته میشود:
$\large S=\int_{t_{0}}^{\infty} d t\left[\frac{1}{2} m \dot{x}(t)^{2}-V(x(t))\right]$
کنش یک تابع است که آرگومانهای آن یک تابع و مقادیر در آن عدد هستند. اصل کنش بیان میکند که مسیر حرکت ذره باید یک نقطه استاتیک باشد. کنش به عنوان انتگرال لاگرانژ در بازه زمانی t1 و t2 برای یک مختصات تعمیم یافته $q=(q_1, q_2, q_3, .\ .\ .\ , q_N)$
تعریف میشود، که مختصات تعمیم یافته تابعی از زمان و مشخص کننده پیکربندی سیستم است.
معادلات هامیلتونی در مکانیک تحلیلی چگونه هستند؟
زمانی که معادلات لاگرانژ را به دست آوردیم، متغیرها و مختصاتی که مورد استفاده قرار دادیم مختصات تعمیم یافته و سرعت تعمیم یافته بودند. لاگرانژ L به عنوان تابعی از این متغیرها به صورت $L(q^i,\dot{q}^i)$) نوشته میشود. این مجموعه از متغیرها یکتا نیستند و برای هر حالت یک انتخاب وجود دارد که به هامیلتونی سیستم بستگی پیدا میکند.
معادلات هامیلتونی معمولاً در مکانیک کوانتومی نیز مورد استفاده قرار میگیرند. همان طور که در قسمتهای قبل نیز گفته شد، تکانه مرتبط با مختصات
$$q^i به صورت زیر معرفی میشود:$\large p_{i}=\frac{\partial L}{\partial \dot{q}^{i}}$
در یک مختصات خط راست همان طور که دیدیم تکانه معمولی برابر با $p_i=m\dot{q}^i$
بود، ولی این موضوع برای مختصاتهای تعمیم یافته دیگر صدق نمیکند. در حال حاضر میخواهیم متغیرهای پایه را از مختصات $q^i$ و سرعت $v^i$ به مختصات و تکانه
$p_i$ تغییر دهیم. به زودی خواهید دید که در زمان تغییر متغیرها اینکه عملگر دیگری غیر از لاگرانژین را در نظر بگیرید، طبیعی است. برای این حالت، شرایطی را در نظر بگیرید که تنها دارای یک مختصات q است. دیفرانسیل لاگرانژی
$L(q,v)$ در این حالت برابر است با:$\large d L=\frac{\partial L}{\partial q} d q+\frac{\partial L}{\partial v} d v=\frac{\partial L}{\partial q} d q+p d v$
در مرجعی که مختصات اصلی و پایه q و p هستند، دیفرانسیل تابع به صورت طبیعی برابر با $adq+bdp$
است که a و b میتوانند هر مقداری داشته باشند. تابع جدید H را به صورت زیر شما مد نظرتون باشه
$\large H=v p-L=\dot{q} p-L$H هامیلتونی است و دیفرانسیل آن برابر است با:
$\large d H=d v p+v d p-d L=d v p+v d p-\frac{\partial L}{\partial q} d q-p d v=-\frac{\partial L}{\partial q} d q+v d p$
بنابراین داریم:
$\large \frac{\partial H}{\partial q}=-\frac{\partial L}{\partial q}, \quad \frac{\partial H}{\partial p}=v=\dot{q}$
تغییر عملگر به شکل بالا که با تغییر متغیر به این صورت همراه است را تبدیلات لژاندر مینامیم. دقت کنید که وقتی متغیرها را به q و p تغییر میدهید، باید تابع H را نیز بر اساس متغیرهای جدید بیان کنیم و بنابراین هر استفاده از v حذف میشود. بدین ترتیب با استفاده از معادله لاگرانژ که به صورت
$\frac{\partial L}{\partial q}=\dot{p}$ است، معادلات هامیلتونی برابر است با:
$\large \dot{q}=\frac{\partial H}{\partial p}, \quad \dot{p}=-\frac{\partial H}{\partial q}$
برای سیستمهای چند ذرهای نیز هامیلتونی به راحتی به دست میآید و تنها لازم است از یک اندیس i برای هر کمیت استفاده کنیم و در نتیجه داریم:
$\large \begin{gathered}
H=\sum_{i} \dot{q}^{i} p_{i}-L \\
\dot{q}^{i}=\frac{\partial H}{\partial p_{i}}, \quad \dot{p}_{i}=-\frac{\partial H}{\partial q^{i}}
\end{gathered}$این مطلب را با بررسی یک مثال به پایان میبریم. یک سیستم خطی در نظر بگیرید که در آن $T=\frac{1}{2}m\dot{x}^2$
و $L=\frac{1}{2}m\dot{x}^2-V(x)$ باشد. در نتیجه
$\frac{\partial L}{\partial \dot{x}}=m\dot{x}$
است و داریم:$\large H=\dot{x} p-L=\frac{p^{2}}{m}-\frac{1}{2} m\left(\frac{p}{m}\right)^{2}+V(x)=\frac{p^{2}}{2 m}+V(x)$
که مجموع انرژی پتانسیل و جنبشی است. این بیان حقیقتاً تا زمانی که وابستگی صریح زمانی بین L و زمان وجود ندارد، کلی است. در نتیجه معادلات هامیلتونی به شکل زیر در میآیند و داریم:$\large \dot{x}=\frac{\partial H}{\partial p}=\frac{p}{m}, \quad \dot{p}=-\frac{d V}{d x}$
دقت کنید که به جای معادلات دیفرانسیل درجه 2 در رابطه بالا معادلات دیفرانسیل درجه 1 داریم. معادله اول برحسب p است و وقتی در معادله دوم قرار داده میشود این شکل هست :$\large m \ddot{x}=-\frac{d V}{d x}$
در مکانیک کلاسیک، محدودیت در یک سیستم پارامتری است که سیستم باید از آن تبعیت کند. به عنوان مثال، جعبه ای که از یک شیب به پایین سر می خورد باید روی شیب باقی بماند. دو نوع محدودیت مختلف وجود دارد: هولونومیک و غیرهولونومیک.نیروهای محدودیت، نیروهایی هستند که جسم محدود کننده بر جسم اعمال می کند تا از محدودیت های حرکتی پیروی کند.حرکت محدود زمانی حاصل می شود که یک جسم مجبور به حرکت به روشی محدود شود. برای مثال، ممکن است مجبور باشد در امتداد یک مسیر منحنی حرکت کند، روی میزی که ممکن است به سمت بالا شتاب بگیرد، بلغزد، با یک گوه شتابدهنده در تماس بماند و غیره.محدودیتها در مکانیک لاگرانی از طریق یکی از دو رویکرد انجام میشوند:
1) از معادله محدودیت برای کاهش درجات آزادی سیستم استفاده می شود. به عنوان مثال، اگر یک ذره به سطح یک کره محدود شود، لاگرانژ را می توان کاملاً بر اساس دو مختصات تعمیم یافته و لحظه ای مرتبط با آنها نوشت (معمولاً، زوایای قطبی و زاویه ای مختصات کروی را به عنوان مختصات تعمیم یافته انتخاب می کنیم. ). نمی توان نیروهای محدودیت را از این طریق پیدا کرد - در نتیجه کاهش پیچیدگی مشکل، به طور ضمنی نادیده گرفته می شوند.
2) از طرف دیگر، یک ضریب لاگرانژ به عنوان درجه آزادی اضافی اضافه می شود. اگر یک L لاگرانژی و تابع قید$f(q_i, t)$ داشته باشیم که به مقداری C محدود شده و تابعی از مختصات تعمیم یافته و زمان باشد، لاگرانژی را به صورت زیر تغییر می دهیم:
$L \mapsto L' = L + \lambda [f(q_i, t) - C]$
استفاده از معادلات اویلر-لاگرانژ در این لاگرانژی جدید L' تمام دینامیک مربوط به سیستم را بازتولید می کند. به طور خاص، به شما امکان می دهد ضریب لاگرانژ λ را حل کنید. با انجام این کار، یافتن نیروهای محدودیت، که هستند، ممکن می شود
$F_i = \lambda \frac{\partial f}{\partial q_i}$
توجه به این نکته مهم است که چنین تابع قید f باید تابعی از زمان و مختصات تعمیم یافته باشد. اصطلاح این نوع محدودیت هولونومیک است. مشکلات مربوط به محدودیت های غیرهولونومیک را نمی توان با این روش درمان کرد.
من کتاب "مکانیک کلاسیک" داگلاس گرگوری را می خوانم و نویسنده می نویسد که استفاده از معادلات نیوتنی برای سیستم های مقید به دو مشکل برخورد می کند.
(1). معادلات حرکت محدودیت ها را در بر نمی گیرد. معادلات نیوتن (در مختصات دکارتی) محدودیت ها را در بر نمی گیرند. بنابراین، اینها باید در قالب شرایط اضافی برای حل همزمان با معادلات دینامیکی گنجانده شوند.
(2). نیروهای محدودیت ناشناخته هستند
و همچنین می نویسد
(1) با مختصات تعمیم یافته غلبه می کند در حالی که (2) با استفاده از معادلات لاگرانژ به جای نیوتن غلبه می شود.
سوالات من این است:
(الف) آیا اساساً (1) و (2) دشواری یکسانی نیست؟ منظورم این است که (1) اگر (2) حل شود مشکلی نیست؟ چرا نویسنده (1) و (2) را تشخیص می دهد؟
(ب) من در مورد آنچه در (1) گفته شده سردرگم هستم. اگر معادلات نیوتن را بدون ادغام قیود بنویسیم، معادلات در اصل «اشتباه» هستند. آیا آنها نیستند؟ تا آنجا که من می دانم، معادلات نیوتن تنها زمانی درست است که همه نیروها مشخص شوند.پاسخ مشخص من به شرح زیر است:
الف) اگر (2) حل شود، (1) به طور جدی یک مشکل نیست، اما همچنان یک ناراحتی بزرگ است، زیرا در مقایسه با مختصات تعمیم یافته باید تعداد بیشتری از معادلات را با متغیرهای بیشتری حل کنید.
به عنوان مثال، اگر می دانید که پسر در یک دایره حرکت می کند، مختصات تعمیم یافته شما q=θ است، زیرا شعاع R ثابت است، اما با استفاده از معادلات نیوتن، باید با مختصات x و y به همراه معادله بپردازید. محدودیت $x^2+y^2=R^2$ (با فرض مرکز دایره به عنوان مبدا).
ب) قانون نیوتن می گوید که $F=\dfrac{dp}{dt}=ma$ محدودیت را می توان یا با یک شرایط اضافی مانند حالت دایره ای بالا، یا با تعیین نیروی محدودیتی که بدن را در مسیر خود نگه می دارد مراقبت کرد. از آنجایی که نیرو تقریباً همیشه ناشناخته است، استفاده از شرط محدودیت ضروری است. همانطور که گفتید، معادله قانون نیوتن صحیح نخواهد بود. در واقع قانون همیشه صحیح است، اما اگر نیرو یا شرایطی وجود نداشته باشد، پاسخ درستی نمی دهد، بنابراین اعمال قانون در چنین مواردی اشتباه است.
یک نکته بی اهمیت: اگر نیروی محدودیت صفر باشد، برای مثال، نیرو $m\dfrac{v^2}{r}$ باشد، هیچ شرایط اضافی لازم نیست، زیرا بدن نه به دلیل محدودیت خاصی، بلکه صرفاً به دلیل نیرو در دایره حرکت می کند. همین وضعیت را می توان از نظر محدودیت ها نیز حل کرد، اما من وارد آن نمی شوم.
محدودیت های هولونومیک و غیرهولونومیک چیست؟اما اغلب می توان یک مختصات را بر حسب مختصات دیگر بیان کرد: به عنوان مثال دو نقطه توسط یک میله صلب به هم متصل می شوند، فاصله نسبی آنها تغییر نمی کند. چنین شرایطی از سیستم را می توان به صورت معادله ای بیان کرد که فقط مختصات مکانی سیستم و زمان را شامل می شود، اما نه بر روی لحظه یا مشتقات بالاتر زمان wrt. به این محدودیت ها هولونومیک می گویند: