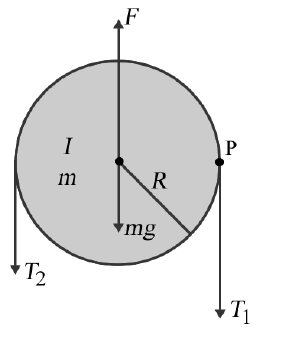
$F = mg + T_1 + T_2 \tag{A1}$تجزیه و تحلیل تورک و انگولار اکسلریشن در مورد اکسل واقعی چرخش و محور پولی اینطورمحاسبه کردم
$τ_{net} = T_1 R − T_2 R = I α \tag{A2}$اگر در مورد نقطه P لبه سمت راست پولی که در آن T1 اعمال میشه تجزیه و تحلیل کنم من محاسبه میکنم $τ_{net} = (F − mg) R − T_2 (2 R) = (I + m R^2
) α \\ {}_\text{WRONG} \tag{A3}$
با استفاده از Eqn. (A1) برای حذف F-mg هم از Eqn. (A3) میده
$τ_{net} = T_1 R − T_2 R = (I + m R^2
) α \\ {}_\text{WRONG} \tag{A4}$
نت توک در Eqns. (A2) و (A4) یکسانه اما ممان اینرسی متفاوته بنابراین انگولار اکسلریشن نیز متفاوته. میدونم که اگر نقطه P را به رشته سمت راست متصل کنم اگر $T_1 ≠ T_2$باشه سپس اکسلریت میگیره سوال من اینه که اگر P را حل کنم همانطور که در فضا به جای یک نقطه متصل به رشته سمت راست ثابته اگر توک را در مورد P بگیرم معادله چگونه خواهد بود.
در (A2) و (A3) به دلیل اکسلریشن مرکز جرم توک را فراموش می کنم. اگر P ثابت باشه مرکز جرم در حال حرکته برای حالت کلی معادلات حرکتی که در یک نقطه دلخواه A جمع میشن نه در مرکز جرم C در حالت سه بعدی هم
$\begin{aligned}\boldsymbol{F}_{{\rm net}} & =\underbrace{m\boldsymbol{a}^{A}}_{\text{linear}}-\underbrace{m\boldsymbol{c}\times\boldsymbol{\alpha}}_{\text{angular}}+\underbrace{\boldsymbol{\omega}\times m\left(\boldsymbol{\omega}\times\boldsymbol{c}\right)}_{\text{centripetal}}\\
\boldsymbol{\tau}_{{\rm net}}^{A} & =\underbrace{{\rm I}^{A}\boldsymbol{\alpha}}_{\text{angular}}+\underbrace{\boldsymbol{c}\times m\boldsymbol{a}^{A}}_{\text{linear}}+\underbrace{\boldsymbol{\omega}\times{\rm I}^{A}\boldsymbol{\omega}}_{\text{gyroscopic}}
\end{aligned} \tag{1}$
میدونم عملیات به معنای محصول متقاطع برداری است. همچنین کمیت های پررنگ بردار هستند در حالی که کمیت های مورب اسکالر هستن
$\begin{array}{c|l}
\text{Symbol} & \text{Description}\\
\hline \boldsymbol{F}_{{\rm net}} & \text{net force vector on body}\\
\boldsymbol{\tau}_{{\rm net}}^{A} & \text{net torque vector on body about point A}\\
m & \text{mass of body}\\
{\rm I}^{A} & \text{mass moment of inertia tensor about A}^{[1]}\\
\boldsymbol{c} & \text{relative position of COM from point A}\\
\boldsymbol{\omega} & \text{angular velocity vector of body}\\
\boldsymbol{a}^{A} & \text{linear acceleration of point A}\\
\boldsymbol{\alpha} & \text{angular acceleration of body}
\end{array}$شرح بردار نیروی شبکه بر بردار گشتاور بدنه روی بدنه در مورد نقطه تجمع توک جرمی تانسور اینرسی در حدود A[1]موقعیت نسبی COM از نقطه بردار انگولار ولوسیتی و لاینر اکسلریشن بدنه نقطه انگولار اکسلریشن جسم [1] تانسور MMOI در A یک ماتریس 3×3 است که از تانسور MMOI در مرکز جرم مشتق میشه چرخش میکنه تا با فریم مختصات اینرسی تراز بشه و با استفاده از COM به نقطه مرجع منتقل میشه. قضیه محور موازی با طرح دو بعدی اصطلاحات ژیروسکوپی ناپدید میشن اما همه اصطلاحات دیگر باید گنجانده بشن. در سوال من وقتی نقطه مرجع نقطه P است فراموش کردم که عبارت خطی را در معادله نت توک قرار بدم. این مربوط به تورک ناشی از اکسلریشن مرکز جرم است.
در دو بعدی معادلات یک معادله برداری برای نیروها و یک معادله اسکالر برای تورک ها هستند.
$\begin{aligned}\boldsymbol{F}_{{\rm net}} & =m\boldsymbol{a}^{A}-m\boldsymbol{c}\,\alpha-m\,\boldsymbol{c}\,\omega^{2}\\
\tau_{{\rm net}}^{A} & =I^{A}\alpha+m\left(c_{\perp}a^{A}\right)
\end{aligned}$
عبارت $m\left(c_{\perp}a^{A}\right)$
در معادلات من گم شده است. اینجا $c_{\perp}$
نشان دهنده فاصله عمود از مرکز جرم تا خطی از نقطه A و در امتداد اکسلریشن وکتور $\boldsymbol{a}^A$ است.
.من توصیه می کنم از انجام پویایی به صورت دو بعدی یا بر اساس کامپوننت خودداری کنین زیرا چیزهایی که ممکنه فرض کنین در دو بعدی لغو میشن ممکنه در واقع لغو نشن. بهتره در ابتدا معادلات حرکت را به صورت سه بعدی مشاهده کنین و در پایان پروجکشن لازم را به صورت دو بعدی انجام بدین. مشکلات در دینامیک دشوار ه زیرا جزئیات زیادی برای در نظر گرفتن وجود داره.
همچنین دینامیک را در مرکز جرم انجام دهید زیرا معادلات حاصل در زمانی که c=0 ساده تر هستند
$\begin{aligned}\boldsymbol{F}_{{\rm net}} & =\underbrace{m\boldsymbol{a}^{C}}_{\text{linear}}\\
\boldsymbol{\tau}_{{\rm net}}^{C} & =\underbrace{{\rm I}^{C}\boldsymbol{\alpha}}_{\text{angular}}+\underbrace{\boldsymbol{\omega}\times{\rm I}^{C}\boldsymbol{\omega}}_{\text{gyroscopic}}
\end{aligned} \tag{2}$
نسخه دوبعدی معادلات (A1) شبیه به آن است. اینجا ${\rm I}^{C}$
تورک جرمی اینرسی در مورد مرکز جرم است.
من فقط برای مواردی که ساده سازی های قابل توجهی وجود داره استفاده از (1) را به جای (2) توصیه میکنم. برخی از نمونه ها عبارتند از، زمانی که جسم غیر چرخشیه
$\small \begin{aligned}\boldsymbol{F}_{{\rm net}} & =\underbrace{m\boldsymbol{a}^{A}}_{\text{linear}}\\
\boldsymbol{\tau}_{{\rm net}}^{A} & =\underbrace{\boldsymbol{c}\times m\boldsymbol{a}^{A}}_{\text{linear}}
\end{aligned}$
یا زمانی که نقطه مرجع ثابت است (غیر متحرک)
$\small \begin{aligned}\boldsymbol{F}_{{\rm net}} & =-\underbrace{m\boldsymbol{c}\times\boldsymbol{\alpha}}_{\text{angular}}+\underbrace{\boldsymbol{\omega}\times m\left(\boldsymbol{\omega}\times\boldsymbol{c}\right)}_{\text{centripetal}}\\
\boldsymbol{\tau}_{{\rm net}}^{A} & =\underbrace{{\rm I}^{A}\boldsymbol{\alpha}}_{\text{angular}}+\underbrace{\boldsymbol{\omega}\times{\rm I}^{A}\boldsymbol{\omega}}_{\text{gyroscopic}}
\end{aligned}$
(1) معادلات حرکت نیوتن اویلر به صورت ماتریسی
$\begin{Bmatrix}\boldsymbol{F}_{{\rm net}}\\
\tau_{{\rm net}}^{A}
\end{Bmatrix}=\begin{bmatrix}m & -m[\boldsymbol{c}\times]\\
m[\boldsymbol{c}\times] & {\rm I}^{A}
\end{bmatrix}\begin{Bmatrix}\boldsymbol{a}^{A}\\
\boldsymbol{\alpha}
\end{Bmatrix}+\begin{Bmatrix}\boldsymbol{\omega}\times m\left(\boldsymbol{\omega}\times\boldsymbol{c}\right)\\
\boldsymbol{\omega}\times{\rm I}^{A}\boldsymbol{\omega}
\end{Bmatrix}$
علاوه بر شکل برداری قضیه محور موازی
${\rm I}^{A}={\rm I}^{C}-m[\boldsymbol{c}\times][\boldsymbol{c}\times]$


